2023.8.6
2022河南萌新联赛第(三)场:河南大学\区间操作.cpp
//题意:定义一个f[x]函数表示一个数分解质因数后各个质因子的幂次和,给定一个长度为n的数组,
//有m个操作,第一种操作是输出[l, r]范围内的a[i]的乘积的f[i],另一种操作是整段区间乘上一个数。
//思路:区间内所有数的乘积的f[i]= 每个数的f[i]的和 (因为数相乘 = 幂次方相加)
//于是们开一个线段树表示区间[l, r]的f[i]和,可以直接查询[l, r]范围内的a[i]的乘积的f[i]。
//对于修改,一个区间乘一个v,如果对v作因数分解,其实就是区间加上因数分解后所有幂次的和,也就是区间加,我们用线段树很容易实现。
//欧拉筛,预处理出范围内所有质数
#include<bits/stdc++.h>#include<iostream>#include<algorithm>#include<map>#include<set>#include<queue>#include<cstring>#include<math.h>#include<map>#include<vector>#include<stack>using namespace std;#define endl '\n'typedef pair<int,int> pr;#define int long long#define ll long long#define fr(i,l,r) for(int i=l;i<=r;i++)#define ufr(i,n,z) for(int i = n;i >= z; i--)#define pb(x) push_back(x)#define all(a) a.begin(),a.end()#define fi first#define se secondconst int N = 1e6+10;const int mod=998244353,inf=LONG_LONG_MAX;int n,m;int a[N];int cnt;int st[N];int prime[N];struct node{int l,r;int sum; //和int flag;}tree[N<<2];void init(){ //欧拉筛for(int i=2;i<N;i++){if(!st[i])prime[cnt++]=i;for(int j=0;i*prime[j]<N;j++){st[i*prime[j]]=1;if(i%prime[j]==0){break;}}}}int get(int x){int ans=0;if(x==1) return 0;for(int i=0;prime[i]*prime[i]<=x;i++){int p=prime[i];if(x%p==0){while(x%p==0){ans++;x/=p;}}}if(x>1)ans++;return ans;}void push_up(int p){tree[p].sum=tree[p<<1].sum+tree[p<<1|1].sum;}void build(int p,int l,int r){tree[p].l=l;tree[p].r=r;if(l==r){tree[p].sum=a[l];return;}int mid=l+r>>1;int f=p<<1;build(f,l,mid);build(f+1,mid+1,r);push_up(p);}void push_down(int p){if(tree[p].flag){int f=p<<1;tree[f].sum+=(tree[f].r-tree[f].l+1)*tree[p].flag;tree[f+1].sum+=(tree[f+1].r-tree[f+1].l+1)*tree[p].flag;tree[f].flag+=tree[p].flag;tree[f+1].flag+=tree[p].flag;tree[p].flag=0;}}void update(int p,int l,int r,int w){if(l<=tree[p].l&&tree[p].r<=r){tree[p].sum+=(tree[p].r-tree[p].l+1)*w;tree[p].flag+=w;return ;}push_down(p);int mid=tree[p].l+tree[p].r>>1;int f=p<<1;if(l<=mid)update(f,l,r,w);if(mid<r)update(f+1,l,r,w);push_up(p);}int query(int p,int l,int r){if(l<=tree[p].l&&tree[p].r<=r){return tree[p].sum;}push_down(p);int ans=0;int mid=tree[p].l+tree[p].r>>1;int f=p<<1;if(l<=mid)ans+=query(f,l,r);if(mid<r)ans+=query(f+1,l,r);return ans;}void solve(){init();int n;cin>>n;fr(i,1,n){cin>>a[i];a[i]=get(a[i]);}build(1,1,n);int q;cin>>q;while(q--){int op,l,r,w;cin>>op>>l>>r;if(op==1){cout<< query(1,l,r)<<'\n';}else{cin>>w;w=get(w);update(1,l,r,w);//cout<<1<<'\n';}}}signed main(){int t=1;// cin>>t;while(t--) solve();return 0;}2022河南萌新联赛第(一)场:河南工业大学\热身小游戏.cpp
//给定一个数n,初始值为1
//给出q次操作,
//1 a,n->n*a
//2 l r撤销第l到r操作中的1操作
//3输出n(mod 1e9+7)
//思路:起初以为是可持久化线段树,特地学了一下,后来发现就是线段树
q次操作看做长度为q的序列,操作1单点修改,操作2区间修改为1,操作3整个区间乘积
#include <bits/stdc++.h>#define fr(i,l,r) for(int i=l;i<=r;i++)using namespace std;#define int long long#define endl "\n"const int max_n = 1e5 + 10;const int inf = 0x3f3f3f3f;const int mod = 1e9 + 7;int n, q;struct Node{int l, r, add, v;} tr[max_n << 2];void pu(int u){tr[u].v = tr[u << 1].v * tr[u << 1 | 1].v % mod;}void pd(int u){if (tr[u].add){tr[u << 1].v = 1, tr[u << 1 | 1].v = 1;tr[u << 1].add = 1, tr[u << 1 | 1].add = 1;tr[u].add = 0;}}void build(int u, int l, int r){tr[u] = {l, r, 0, 1};if (l == r)return;int mid = l + r >> 1;build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);pu(u);}void modify(int u, int l, int r, int c){if (tr[u].l >= l && tr[u].r <= r){tr[u].add = c;tr[u].v = c;return;}pd(u);int mid = tr[u].l + tr[u].r >> 1;if (l <= mid)modify(u << 1, l, r, c);if (r > mid)modify(u << 1 | 1, l, r, c);pu(u);}signed main(){ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cin >> q;build(1, 1, q);for (int i = 1; i <= q; i++){int op;cin >> op;if (op == 1){int a;cin >> a;modify(1, i, i, a); //此处单点修改不影响push_down,影响push_up}else if (op == 2){int l, r;cin >> l >> r;modify(1, l, r, 1);}else if (op == 3)cout << tr[1].v % mod << endl;}return 0;}P3919 【模板】可持久化线段树 1(可持久化数组)
维护长度为N的数组的值,支持以下操作
修改某个历史版本的值,访问某个历史版本的值
v 1 loc value在版本v上将aloc的值改为value
v 2 loc在版本v上访问aloc的值
动态开点的方法存储每个点的左右子节点
显然对于每一次修改,我们都需要创造出一个新的树根 root
然后显然对于新的线段树中的任意节点,如果以该节点代表的区间中不包含被修改的节点,那么也就意味着以这个节点为根的子树不需要修改。
于是我们就可以让这个节点的父亲节点的与这个节点对应的儿子直接指向修改前的线段树上的该节点。
若该节点即对应被修改的节点,那么就可以直接建立新节点。
若该节点对应的区间中包含该节点,那么我们再对该节点的左右儿子分别处理即可。
#include<bits/stdc++.h>
using namespace std;
const int N = 2e6 + 10;
struct node {int l, r, t;
}tree[N << 4];
int n, m, tot, a[N], root[N];//Root[i]为版本i的线段树根节点
void build(int& p, int l, int r)
{p = ++tot;//给节点赋编号if (l == r) {//若当前节点只对应一点tree[p].t = a[l];return;}int mid = (l + r) >> 1;build(tree[p].l, l, mid);build(tree[p].r, mid + 1, r);
}
void insert(int& p, int l, int r, int pos, int val, int now)//插入,now为版本,pos为修改点位置
{tree[p = ++tot] = tree[now];//使当前路径上的点等于原来版本上的对应点if (l == r) {tree[p].t = val;return;}int mid = (l + r) >> 1;if (pos <= mid)insert(tree[p].l, l, mid, pos, val, tree[now].l);elseinsert(tree[p].r, mid + 1, r, pos, val, tree[now].r);
}
int query(int p, int l, int r, int pos)
{if (l == r)return tree[p].t;int mid = (l + r) >> 1;if (pos <= mid)return query(tree[p].l, l, mid, pos);elsereturn query(tree[p].r, mid + 1, r, pos);
}
int main()
{scanf("%d%d", &n, &m);for (int i = 1; i <= n; ++i)scanf("%d", a + i);build(root[0], 1, n);for (int i = 1; i <= m; ++i) {int opt, v, loc, val;//opt为操作种类,v为版本,loc为修改/查询点位置,val为修改值scanf("%d%d%d", &v, &opt, &loc);if (opt == 1) {scanf("%d", &val);insert(root[i], 1, n, loc, val, root[v]);}elseprintf("%d\n", query(root[i] = root[v], 1, n, loc));//查询,同时因为查询生成不变的新版本所以Root[i]=Root[v]}return 0;
}牛客\多校\2022河南萌新联赛第(二)场:河南理工大学\数对.cpp
//给定2e5的数列,x,y
//1<=l<=r<=n
//求多少对(l,r)满足al+...+ar<=x+y*(r-l+1) (-1e9<=ai<=1e9)
//思路:转化成(al-y)+....+(ar-y)<=x,令bi=ai-y,求前缀和
//进一步转化成sumr-suml<=x,sumr-x<=suml,枚举右端点,每次累加树状数组大于等于sumr-x的个数
//值域很大,树状数组装不下,考虑离散化
#include<bits/stdc++.h>#include<iostream>#include<algorithm>#include<map>#include<set>#include<queue>#include<cstring>#include<math.h>#include<map>#include<vector>#include<stack>using namespace std;#define endl '\n'typedef pair<int,int> pr;#define int long long#define ll long long#define fr(i,l,r) for(int i=l;i<=r;i++)#define ufr(i,n,z) for(int i = n;i >= z; i--)#define pb(x) push_back(x)#define all(a) a.begin(),a.end()#define fi first#define se secondconst int N = 1e6+10;const int mod=998244353,inf=LONG_LONG_MAX;int n,m;int a[N];int tree[N];int sum[N];vector<int>v;int lowbit(int x){return x&(-x);}void add(int x){for(int i=x;i<N;i+=i&-i){tree[i]+=1;}}int query(int x){int ans=0;for(int i=x;i;i-=i&-i){ans+=tree[i];}return ans;}int get(int x){return lower_bound(v.begin(),v.end(),x)-v.begin()+1;}void solve(){int x,y;cin>>n>>x>>y;fr(i,1,n){cin>>sum[i];sum[i]+=sum[i-1]-y;}fr(i,0,n){v.push_back(sum[i]);v.push_back(sum[i]-x);}sort(v.begin(),v.end());v.erase(unique(v.begin(),v.end()),v.end());int ans=0;fr(i,0,n){ans+=i-query(get(sum[i]-x)-1);add(get(sum[i]));}cout<<ans<<'\n';}signed main(){int t=1;// cin>>t;while(t--) solve();return 0;}相关文章:

2023.8.6
2022河南萌新联赛第(三)场:河南大学\区间操作.cpp //题意:定义一个f[x]函数表示一个数分解质因数后各个质因子的幂次和,给定一个长度为n的数组, //有m个操作,第一种操作是输出[l, r]范围内的a…...

kubernetes网络之网络策略-----Network Policies - Default
默认情况下,如果名称空间中没有配置 NetworkPolicy,则该名称空间中,所有Pod的所有入方向流量和所有出方向流量都是被允许的。 那么如果我们想改变名称空间中默认的网络策略,又该怎么做呢? 默认拒绝所有的入方向流量 …...
奥威BI系统|秒分析,更适合分析大数据
根据以往的经验,当数据量多到一定程度就容易导致系统卡顿、崩溃。这种现象给企业级数据分析造成了极大的困扰。随着业务发展扩大和分析需求精细化,企业需要一套能秒分析大数据的系统。而奥威BI系统就是这样一款可以秒分析大数据的商业智能系统。 奥威BI…...
安全作业-Race竞争型漏洞、原型链污染
1.race漏洞一直卡在虚拟机安装上(待研究) 2.原型链污染 一、第一题js代码 const express require(express) var hbs require(hbs); var bodyParser require(body-parser); const md5 require(md5); var morganBody require(morgan-body); const app express(); var use…...

对微服务网关的一些总结
对微服务网关的一些总结 一. 什么是网关 网关是位于NGINX(或没有)与真实微服务间的转发服务。 用户通过HTTP接口,连接到NGINX,然后NGINX反向到M个网关。 网关根据[服务注册与发现],进行转发请求到具体的微服务上。 由于网关可编码&#…...
该选择WPF 还是 Winform?
WPF和WinForms都是.NET平台下的桌面应用程序开发框架,它们各有特点,适用于不同的场景和需求。下面是对WPF和WinForms的一些比较和优劣势:WPF(Windows Presentation Foundation):WPF具有强大的图形渲染能力&…...

概念解析 | ChatGPT技术概览
注1:本文系“概念解析”系列之一,致力于简洁清晰地解释、辨析复杂而专业的概念。本次辨析的概念是:ChatGPT技术概览 参考资料:Deng J, Lin Y. The benefits and challenges of ChatGPT: An overview[J]. Frontiers in Computing and Intelligent Systems, 2022, 2(2): 81-83. …...

用Rust实现23种设计模式之 代理模式
关注我,学习Rust不迷路!! 代理模式是一种结构型设计模式,它允许通过代理对象来控制对真实对象的访问。以下是代理模式的优点和使用场景: 优点: 控制访问:代理模式可以控制对真实对象的访问&a…...

【nlp pytorch】基于标注信息从句子中提取命名实体内容
基于标注信息从句子中提取实体内容 1 需求2 代码实现3 代码封装1 需求 给定一个句子和已经通过模型训练标注好的信息,从而提取出句子中的实体内容,如下 输入: (1)句子信息 每个糖尿病患者,无论是病情轻重,不论是注射胰岛素,还是口服降糖药,都必须合理地控制饮食。(2)…...

图为科技加入深圳市智能交通行业协会 ,打 …
图为科技加入深圳市智能交通行业协会,打造智能交通新生态! 交通是国民经济发展的“大动脉”,交通拥堵、事故频发等问题不仅影响了人们的出行体验,也对经济的发展产生了负面影响。安全、高效、便捷的出行,一直是人们的…...

大模型排行榜及相关基础技术
大模型排行榜 测试集CEval中文多个学科测试集排名MMLU大规模多任务语言理解英文排名,介绍斯坦福排行榜 强人工智能AGI相关基础技术 标题简介分类稳定扩散模型The Illustrated Stable Diffusion图示化讲解Jay讲解Stable Diffusion计算机技术资料Transformer图示化讲解…...

Python入门【try和except结构、常见异常、with上下文管理 、traceback模块和生成异常日志、自定义异常类】(十八)
👏作者简介:大家好,我是爱敲代码的小王,CSDN博客博主,Python小白 📕系列专栏:python入门到实战、Python爬虫开发、Python办公自动化、Python数据分析、Python前后端开发 📧如果文章知识点有错误…...

windows脚本获取管理员权限修改host
很多时候我们常常需要通过管理员权限执行脚本,脚本可能涉及到一些受保护信息的访问,我们写个简单的脚本来更改host文件,host文件就是需要管理员权限才能访问的启动脚本时先检查是否有管理员权限,如果没有就调用授权脚本进行管理员…...

Flask简介与基础入门
一、了解框架 Flask作为Web框架,它的作用主要是为了开发Web应用程序。那么我们首先来了解下Web应用程序。Web应用程序 (World Wide Web)诞生最初的目的,是为了利用互联网交流工作文档。 1、一切从客户端发起请求开始。 所有Flask程序都必须创建一个程序…...
Stable Diffusion 硬核生存指南:WebUI 中的 GFPGAN
本篇文章聊聊 Stable Diffusion WebUI 中的核心组件,强壮的人脸图像面部画面修复模型 GFPGAN 相关的事情。 写在前面 本篇文章的主角是开源项目 TencentARC/GFPGAN,和上一篇文章《Stable Diffusion 硬核生存指南:WebUI 中的 CodeFormer》提…...
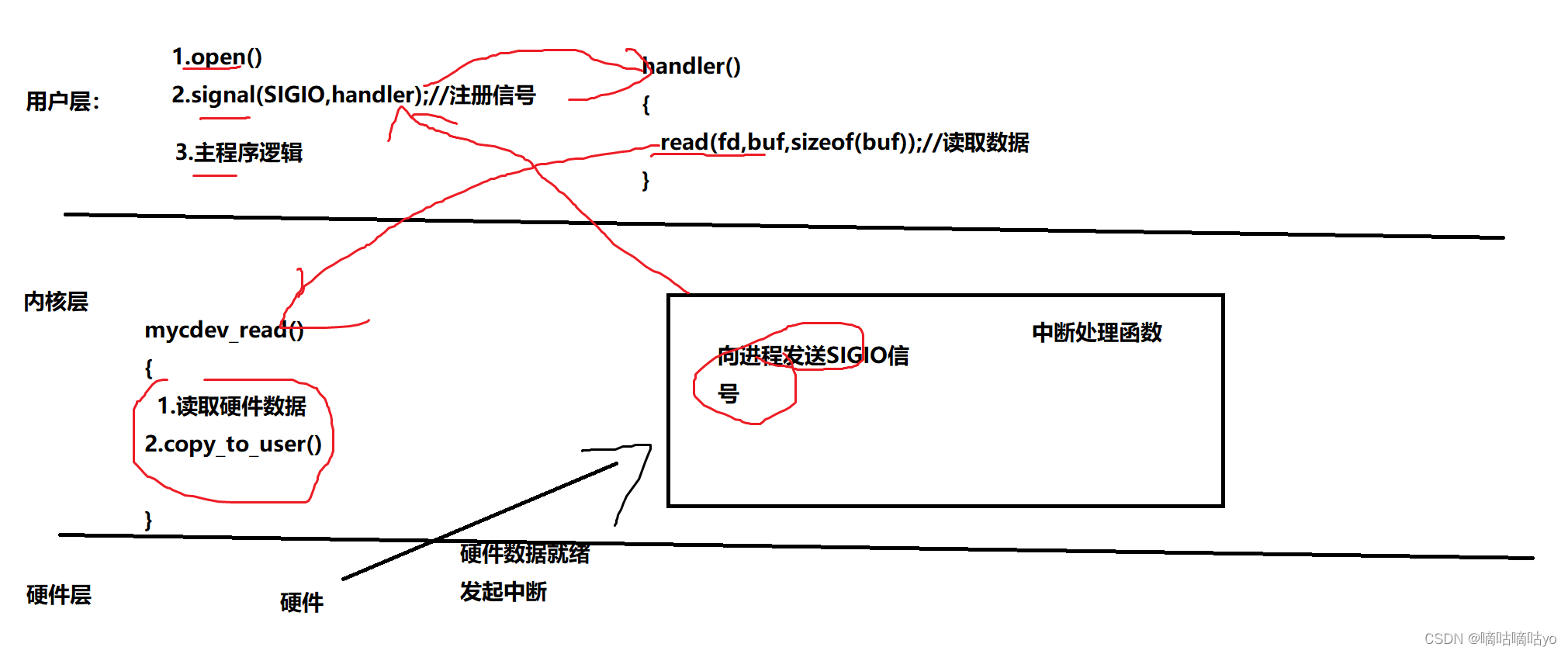
IO模型-信号驱动IO
linux内核中存在一个信号SIGIO,这个信号就是用于实现信号驱动IO的。当应用程序中想要以信号驱动IO的模型读写硬件数据时,首先注册一个SIGIO信号的信号处理函数,当硬件数据就绪,硬件会发起一个中断,在硬件的中断处理函数中向当前进…...
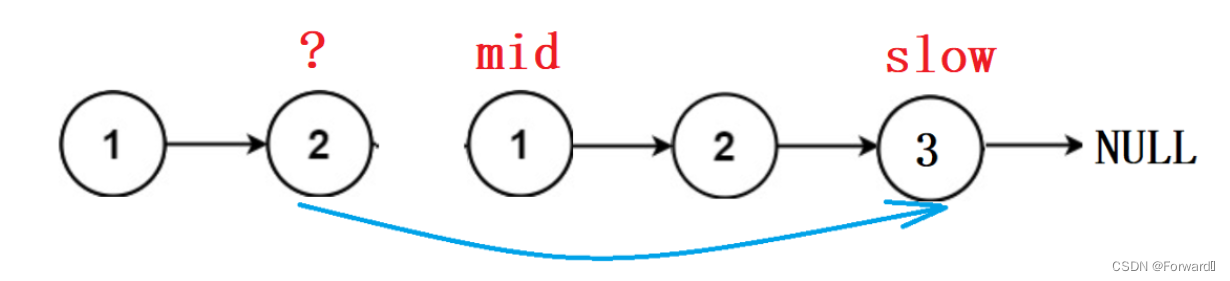
每日一题——回文链表
回文链表 题目链接 回文结构即字符串正序逆序完全一致,如“1 2 3 4 3 2 1”,那么我们就要想办法同时比较链表头和链表尾的元素,看其是否相等。 下面介绍一种最常用的方法: 思路 如果我们仔细观察回文结构,就会得到一…...

OPENCV C++(一) 二进制和灰度原理 处理每个像素点值的方法
#include <opencv2/opencv.hpp> using namespace std; using namespace cv;必须包含的头文件! 才能开始编写代码 读取相片 一般来说加个保护程序 不至于出error和卡死 Mat image imread("test.webp"); //存放自己图像的路径 if (image.empty()){p…...
Python GUI编程(Tkinter)
Python GUI编程(Tkinter) Python 提供了多个图形开发界面的库,几个常用 Python GUI 库如下: Tkinter: Tkinter 模块(Tk 接口)是 Python 的标准 Tk GUI 工具包的接口 .Tk 和 Tkinter 可以在大多数的 Unix 平台下使用,同样可以应用在 Windows …...

K8S简介
目录 前言K8S 简介K8S 是什么作用Kubernetes 主要功能如下:Kubernetes 集群架构与组件 核心组件Master 组件Kube-apiserverKube-controller-managerKube-scheduler配置存储中心 etcd Node 组件KubeletKube-Proxydocker 或 rocket Kubernetes 核心概念PodPod控制器La…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...

在golang中如何将已安装的依赖降级处理,比如:将 go-ansible/v2@v2.2.0 更换为 go-ansible/@v1.1.7
在 Go 项目中降级 go-ansible 从 v2.2.0 到 v1.1.7 具体步骤: 第一步: 修改 go.mod 文件 // 原 v2 版本声明 require github.com/apenella/go-ansible/v2 v2.2.0 替换为: // 改为 v…...
