自监督去噪:Neighbor2Neighbor原理分析与总结

文章目录
- 1. 方法原理
- 1.1 先前方法总结
- 1.2 Noise2Noise回顾
- 1.3 从Noise2Noise到Neighbor2Neighbor
- 1.4 框架结构
- 2. 实验结果
- 3. 总结
文章链接:https://arxiv.org/abs/2101.02824
参考博客:https://arxiv.org/abs/2101.02824
1. 方法原理
1.1 先前方法总结
- 监督学习的方法:noisy-clean训练方法数据集构建存在问题、泛化性不好,真实场景基本用不了。
- Noise2Noise系列:每个场景需要配对的噪声数据。应用上会有局限性,比如室内静态场景。
- 现有的自监督学习方法:
- 从单张图片上挖掘信息:DIP系列,Self2Self,Noisy-as-Clean
- Noise2Noise系列:N2N,Noise2Void,Noise2Self,问题在于网络训练困难、会损失有用信息、依赖于噪声模型
- 噪声建模方法:Probabilistic Noise2Void,Laine19,Dilated Blind-Spot预测噪声分布,在实际中很难应用
1.2 Noise2Noise回顾
Noise2Noise不需要噪声图片,基于多张独立的噪声图像就去噪, 具体内容可以参考:Noise2Noise 笔记
-
Noise2Noise的局限在于:需要采集同一个场景下多个图像,着对于动态场景(户外或者自拍)是非常困难的。
-
Neighbor2Nieghbor的动机就是解决上述问题,有两个假设/想法:
- Noise2Noise是对同一场景进行多次采样训练 --> 对相似的场景进行多个采样然后进行训练 --> 降低数据采集的难度
- 是否能够只使用一张含噪声图像就训练网络
1.3 从Noise2Noise到Neighbor2Neighbor
Noise2Noise的最大似然估计
a r g m i n θ E x , y , z ∣ ∣ f θ ( y ) − z ∣ ∣ \underset{\theta}{argmin} E_{x,y,z}||f_{\theta}(y) - z|| θargminEx,y,z∣∣fθ(y)−z∣∣
由于Noise2Noise要求一个场景(x)至少两个独立含噪的图片( y , z y,z y,z),这在真实场景中很难满足,所以需要考虑扩展理论:
- 同一场景两个独立含噪图像 --> 相似场景两张独立含噪声图像
- 每个场景多张含噪图像–> 每个场景单张含噪图像
相似场景配对噪声图片进行去噪
将 Noise2Noise的概念拓展一下:假设有一张干净图片 x x x, 一张含噪图像是 y y y,另一张含噪图像z上还有一些别的偏差
ϵ : = E z ∣ x ( z ) − E y ∣ x ( y ) ≠ 0 \epsilon := E_{z|x}(z) - E_{y|x}(y) \neq 0 ϵ:=Ez∣x(z)−Ey∣x(y)=0
第一个定理:用 y和z表示x上的两个噪声数据,并且考虑 ϵ ≠ 0 \epsilon \neq 0 ϵ=0: E y ∣ x ( y ) = x E_{y|x}(y) = x Ey∣x(y)=x 和 E z ∣ x ( z ) = x + ϵ E_{z|x}(z) = x + \epsilon Ez∣x(z)=x+ϵ, 其中z的方差为 σ z 2 \sigma_z^2 σz2。那么有:
E x , y ∣ ∣ f θ ( y ) − x ∣ ∣ 2 2 = E x , y , z ∣ ∣ f θ ( y ) − z ∣ ∣ 2 2 − σ z 2 + 2 ϵ E x , y ( f θ ( y ) − x ) E_{x,y}||f_{\theta}(y) - x||_2^2 = E_{x,y,z}||f_{\theta}(y) - z||_2^2 - \sigma_z^2 + 2\epsilon E_{x,y}(f_{\theta}(y) - x) Ex,y∣∣fθ(y)−x∣∣22=Ex,y,z∣∣fθ(y)−z∣∣22−σz2+2ϵEx,y(fθ(y)−x)
- 当噪声图片之间的偏差 ϵ ≠ 0 \epsilon \neq 0 ϵ=0的时候(也就是 E x , y ( f θ ( y ) − x ) ≠ 0 E_{x,y}(f_{\theta}(y) - x) \neq 0 Ex,y(fθ(y)−x)=0),优化Noise2Noise网络的 E x , y , z ∣ ∣ f θ ( y ) − z ∣ ∣ 2 2 E_{x,y,z}||f_{\theta}(y) - z||_2^2 Ex,y,z∣∣fθ(y)−z∣∣22不会得到和监督学习 E x , y ( f θ ( y ) − x ) E_{x,y}(f_{\theta}(y) - x) Ex,y(fθ(y)−x) 相同的结果。
- 但是当 ϵ → 0 \epsilon \rightarrow 0 ϵ→0时, 2 ϵ E x , y ( f θ ( y ) − x ) → 0 2\epsilon E_{x,y}(f_{\theta}(y) - x) \rightarrow 0 2ϵEx,y(fθ(y)−x)→0, 也就是说Noise2Noise网络训练的结果和监督学习训练的结果是近似的。(这里需要注意一个点, σ z \sigma_z σz是一个常数,优化过程不影响)
上面其实是Noise2Noise工作的原理,但是需要一对噪声数据
对于单张含噪图像而言,构造两张"相似但不相同"的图像的一种可行方法是采样。在原图的相邻但不相同的位置采样出来的子图很显然满足了相互之间的差异很小,但是其对应的干净图像并不相同的条件( ϵ → 0 \epsilon \rightarrow 0 ϵ→0)。给定含噪图像y,我们从中采样两次得到噪声对( g 1 ( y ) , g 2 ( y ) g_1(y),g_2(y) g1(y),g2(y)),用Noise2Noise的方式训练有:
a r g m i n θ E x , y ∣ ∣ f θ ( g 1 ( y ) ) − g 2 ( y ) ∣ ∣ 2 \underset{\theta}{argmin} E_{x,y} ||f_{\theta}(g_1(y)) - g_2(y)||^2 θargminEx,y∣∣fθ(g1(y))−g2(y)∣∣2
这种方法称为 Pseudo Noise2Noise ,但是由于 g 1 ( y ) , g 2 ( y ) g_1(y), g_2(y) g1(y),g2(y) 采样的位置不同,其偏差不等于0:
ϵ = E y ∣ x ( g 2 ( y ) ) − E y ∣ x ( g 1 ( y ) ) ≠ 0 \epsilon = E_{y|x}(g_2(y)) - E_{y|x}(g_1(y)) \neq 0 ϵ=Ey∣x(g2(y))−Ey∣x(g1(y))=0
直接用Noise2Noise的方法训练得到的结果不是理想结果,且容易导致过度平滑。因此Neighbor2Neighbor考虑在其上加正则项进行约束。假设一个理想的降噪网络 f θ ∗ f_{\theta}^* fθ∗,其具有理想降噪能力
f θ ∗ ( y ) = x f_{\theta}^* (y) = x fθ∗(y)=x
f θ ∗ ( g l ( y ) ) = g l ( x ) f_{\theta}^* (g_l(y)) = g_l(x) fθ∗(gl(y))=gl(x)
这个理想的降噪网络满足:
E y ∣ x { f θ ∗ ( g 1 ( y ) ) − g 2 ( y ) − ( g 1 ( f θ ∗ ( y ) ) − g 2 ( f θ ∗ ( y ) ) ) } = g 1 ( x ) − E y ∣ x { g 2 ( y ) } − ( g 1 ( x ) − g 2 ( x ) ) = g 2 ( x ) − E y ∣ x { g x ( y ) } = 0 \begin{aligned} &E_{y|x} \{ f_{\theta}^* (g_1(y)) - g_2(y) - (g_1(f_{\theta}^*(y)) -g_2(f_{\theta}^*(y))) \}\\ &= g_1(x) - E_{y|x}\{ g_2(y)\} - (g_1(x) - g_2(x)) \\ &= g_2(x) - E_{y|x}\{ g_x(y)\} \\ &= 0 \end{aligned} Ey∣x{fθ∗(g1(y))−g2(y)−(g1(fθ∗(y))−g2(fθ∗(y)))}=g1(x)−Ey∣x{g2(y)}−(g1(x)−g2(x))=g2(x)−Ey∣x{gx(y)}=0
因此考虑在 Pseudo Noise2Noise网络中添加一个约束
a r g m i n θ E y ∣ x ∣ ∣ f θ ( g 1 ( y ) ) − g 2 ( y ) ∣ ∣ 2 2 \underset{\theta}{argmin} E_{y|x} ||f_{\theta}(g_1(y)) - g_2(y)||_2^2 θargminEy∣x∣∣fθ(g1(y))−g2(y)∣∣22
s . t . E y ∣ x { f θ ( g 1 ( y ) ) − g 2 ( y ) − ( g 1 ( f θ ( y ) ) − g 2 ( f θ ( y ) ) ) } = 0 s.t. \;\; E_{y|x} \{ f_{\theta} (g_1(y)) - g_2(y) - (g_1(f_{\theta}(y)) -g_2(f_{\theta}(y))) \} = 0 s.t.Ey∣x{fθ(g1(y))−g2(y)−(g1(fθ(y))−g2(fθ(y)))}=0
最后将带约束的优化转换为带正则的优化问题:
a r g m i n θ E y ∣ x ∣ ∣ f θ ( g 1 ( y ) ) − g 2 ( y ) ∣ ∣ 2 2 + γ E y ∣ x ∣ ∣ f θ ( g 1 ( y ) ) − g 2 ( y ) − ( g 1 ( f θ ( y ) ) − g 2 ( f θ ( y ) ) ) ∣ ∣ 2 2 \underset{\theta}{argmin} E_{y|x} ||f_{\theta}(g_1(y)) - g_2(y)||_2^2 + \gamma E_{y|x} || f_{\theta} (g_1(y)) - g_2(y) - (g_1(f_{\theta}(y)) -g_2(f_{\theta}(y))) ||_2^2 θargminEy∣x∣∣fθ(g1(y))−g2(y)∣∣22+γEy∣x∣∣fθ(g1(y))−g2(y)−(g1(fθ(y))−g2(fθ(y)))∣∣22
1.4 框架结构
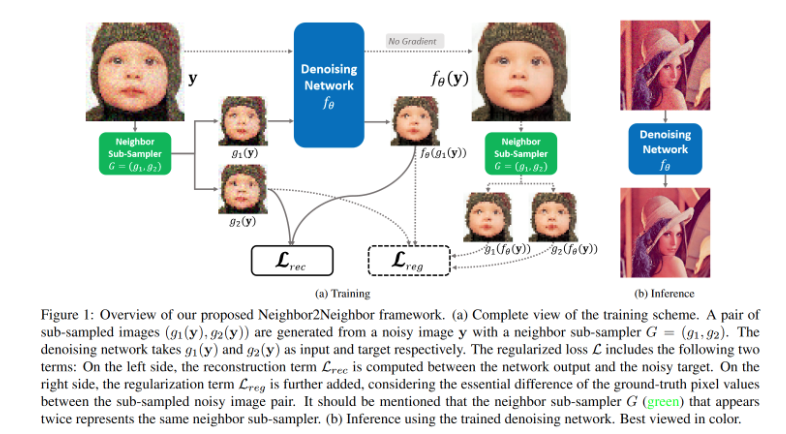
具体而言:
- 从单张含噪图像上通过采样器G构造两个子图( g 1 ( y ) , g 2 ( y ) g_1(y),g_2(y) g1(y),g2(y)),通过着两个子图构建重构损失函数(1.3推导)
- 对原图进行推理降噪,得到的降噪图像再通过相同的采样方法得到两张子图,计算正则项
对于采样器G:设计了近邻采样,即将图像分为2*2的单元,再每个单元中随机选择两个紧邻像素分别划分到两个子图之中,这样构建处两个“相似但是不同”的子图。
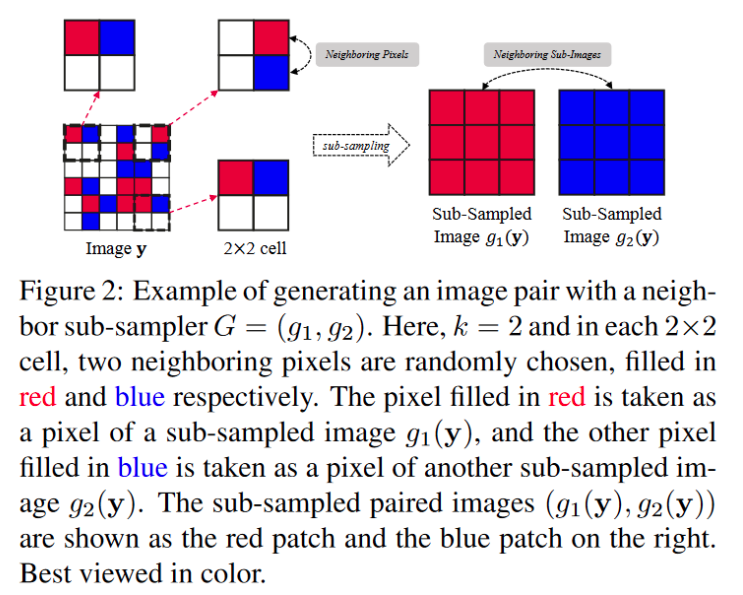
2. 实验结果
分别测试了Gaussian和Poisson噪声,每种噪声分别尝试了固定噪声水平和动态噪声水平两种情况。结果表明,在多个测试集上,本方法在性能上比使用配对数据训练的方法(N2C)低0.3dB左右,超越了现有的自监督降噪方法。在动态噪声水平的场景下,显著超越其他自监督方法,甚至与自监督+后处理的Laine19不相上下。

消融实验说明正则化的有效性:当权重为0时,Neighbor2Neighbor退化为pseudo Noise2Noise,此时模型的PSNR/SSIM水平较低,而网络输出的图像过于模糊而损失了大部分的细节信息;随着权重增加,模型的PSNR/SSIM开始提高,此时降噪的图像开始保留更多的细节,但是噪声也被更多地保留下来。而当权重太大的时候,模型的PSNR/SSIM开始降低,而降噪图像也变得更加Noisy。由此可见,正则项起到了平衡降噪能力和细节保留的作用。针对不同的场景,选择合适的权重,可以发挥出Neighbor2Neighbor的最佳效果。

3. 总结
- 提出了基于采样配对的 Noise2Noise去噪训练方法,使用添加正则化的方法消除不同采样之间的偏差( ϵ \epsilon ϵ)
- 采样的策略后续也被应用到 Blind2Unblid工作之中了
- 强假设仍然存在,影响方法的泛化性
- 噪声是零均值的
相关文章:

自监督去噪:Neighbor2Neighbor原理分析与总结
文章目录 1. 方法原理1.1 先前方法总结1.2 Noise2Noise回顾1.3 从Noise2Noise到Neighbor2Neighbor1.4 框架结构2. 实验结果3. 总结 文章链接:https://arxiv.org/abs/2101.02824 参考博客:https://arxiv.org/abs/2101.02824 1. 方法原理 1.1 先前方法总…...
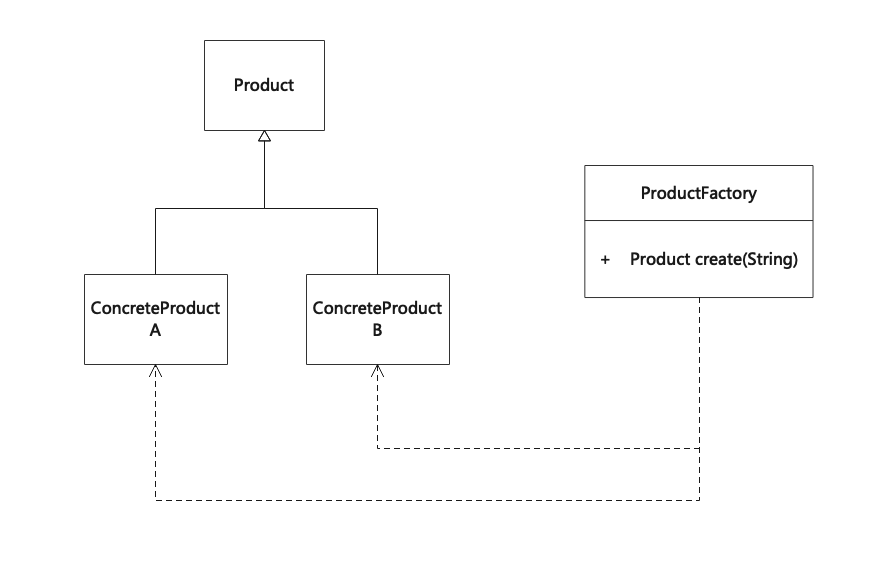
简单工厂模式(Simple Factory)
简单工厂模式,又称为静态工厂方法(Static Factory Method)模式。在简单工厂模式中,可以根据参数的不同返回不同类的实例。简单工厂模式专门定义一个类来负责创建其他类的实例,被创建的实例通常都具有共同的父类。简单工厂模式不属于GoF的23个…...

Agent:OpenAI的下一步,亚马逊云科技站在第5层
什么是Agent?在大模型语境下,可以理解成能自主理解、规划、执行复杂任务的系统。Agent也将成为新的起点,成为各行各业构建新一代AI应用必不可少的组成部分。 对此,初创公司Seednapse AI创始人提出构建AI应用的五层基石理论&#…...
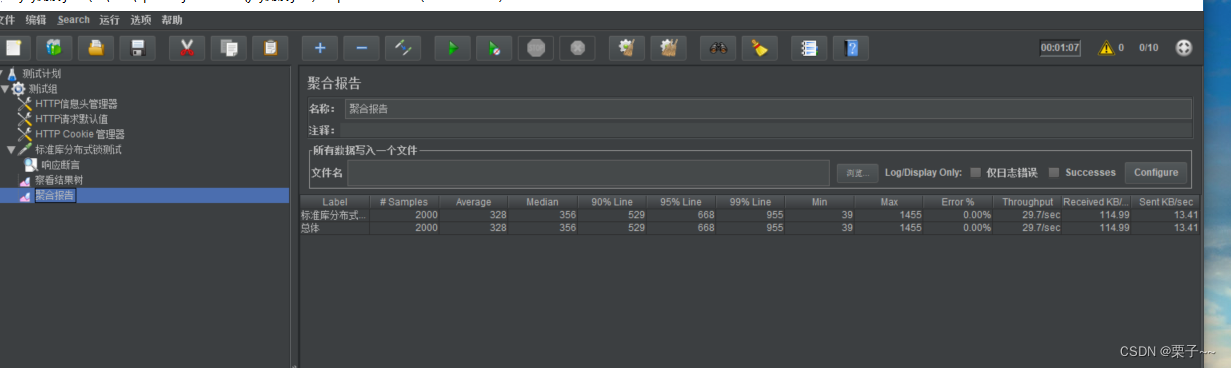
JMeter 4.x 简单使用
文章目录 前言JMeter 4.x 简单使用1. 启动2. 设置成中文3. 接口测试3.1. 设置线程组3.2. HTTP信息请求头管理器3.3. 添加HTTP请求默认值3.4. 添加HTTP cookie 管理3.5. 添加http请求3.5.1. 添加断言 3.6. 添加监听器-查看结果树3.7. 添加监听器-聚合报告 4. 测试 前言 如果您觉…...

深入NLTK:Python自然语言处理库高级教程
在前面的初级和中级教程中,我们了解了NLTK库中的基本和进阶功能,如词干提取、词形还原、n-gram模型和词云的绘制等。在本篇高级教程中,我们将深入探索NLTK的更多高级功能,包括句法解析、命名实体识别、情感分析以及文本分类。 一…...

React 用来解析html 标签的方法
在React中,解析HTML标签通常是使用JSX(JavaScript XML)语法的一部分。JSX允许您在JavaScript代码中编写类似HTML的标记,然后通过React进行解析和渲染。 以下是React中解析HTML标签的几种常见方式: 直接在JSX中使用标…...
【C++】做一个飞机空战小游戏(五)——getch()控制两个飞机图标移动(控制光标位置)
[导读]本系列博文内容链接如下: 【C】做一个飞机空战小游戏(一)——使用getch()函数获得键盘码值 【C】做一个飞机空战小游戏(二)——利用getch()函数实现键盘控制单个字符移动【C】做一个飞机空战小游戏(三)——getch()函数控制任意造型飞机图标移动 【C】做一个飞…...
Flask 是什么?Flask框架详解及实践指南
Flask 是一个轻量级的 Python Web 框架,它被广泛用于构建 Web 应用程序和 API。Flask 简单易用,具有灵活性和可扩展性,是许多开发者喜欢用其构建项目的原因。本文将介绍 Flask 是什么以及如何使用它来构建 Web 应用程序,同时提供一…...
C. Mark and His Unfinished Essay - 思维
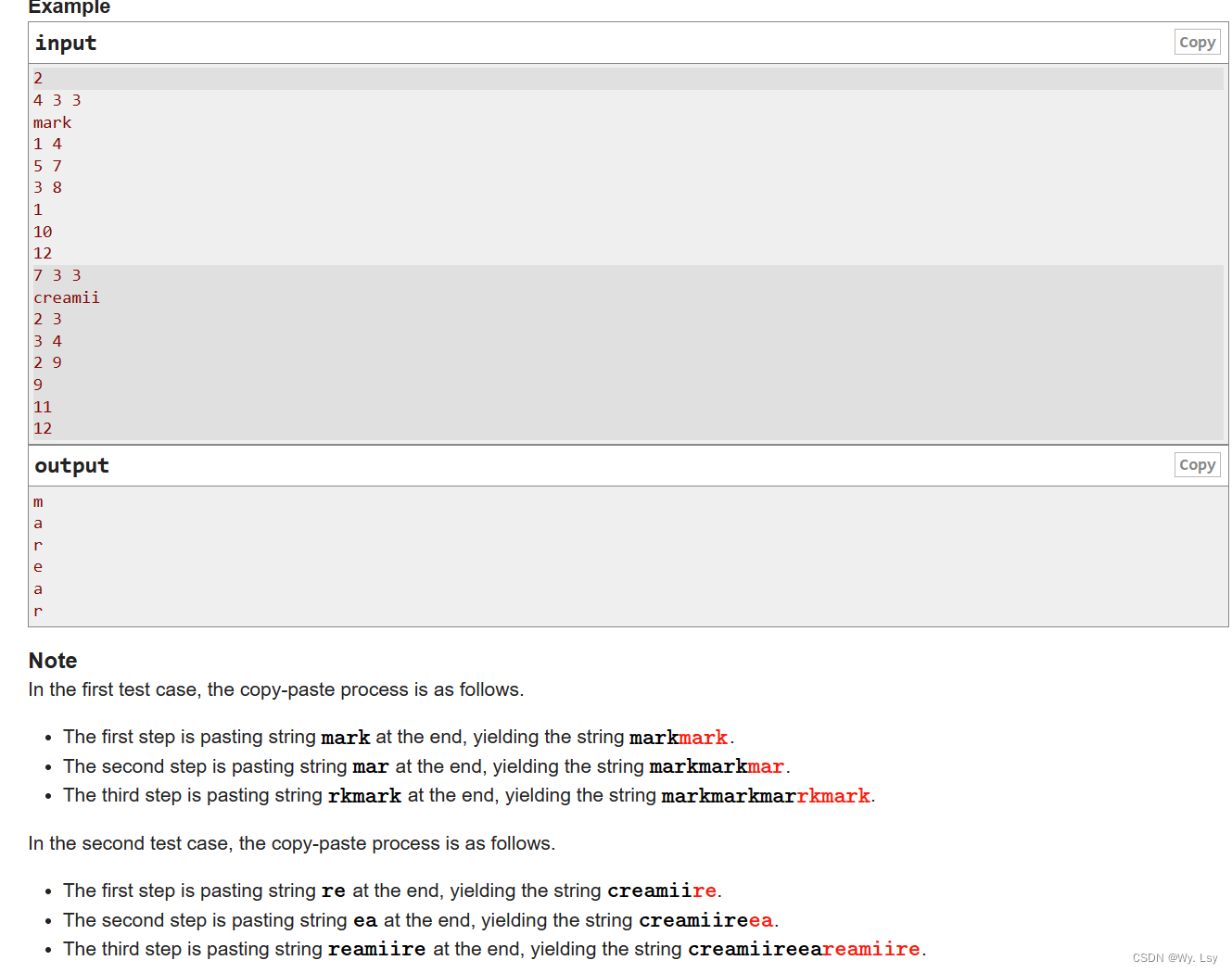
分析: 直接模拟操作会mle,可以每次复制记录对应源字符串的下标,可以记录每次字符串增加的长度的左右端点下标,可以发现左端点与读入的l是对应的,因此就可以向前移到l的位置,这样层层递归,就能找…...

Java的变量与常量
目录 变量 声明变量 变量的声明类型 变量的声明方式:变量名 变量名的标识符 初始化变量 常量 关键字final 类常量 总结 变量和常量都是用来存储值和数据的基本数据类型存储方式,但二者之间有一些关键差别。 变量 在Java中,每个变…...
C# Blazor 学习笔记(6):热重置问题解决
文章目录 前言热重置问题描述解决方法演示 总结 前言 我最近在使用Blazor的时候,使用了BootstrapBlazor(以下简称BB)创建模板的时候,发现热重置无效。经过了一上午的折腾,我终于解决了这个问题。 热重置 问题描述 …...

一百四十六、Xmanager——Xmanager5连接Xshell7并控制服务器桌面
一、目的 由于kettle安装在Linux上,Xshell启动后需要Xmanager。而Xmanager7版本受限、没有免费版,所以就用Xmanager5去连接Xshell7 二、Xmanager5安装包来源 (一)注册码 注册码:101210-450789-147200 (…...

用Rust实现23种设计模式之 模板方法模式
关注我,学习Rust不迷路!! 模板方法模式是一种行为型设计模式,它定义了一个算法的骨架,将一些步骤的实现延迟到子类中。以下是模板方法模式的优点和使用场景: 优点: 提高代码复用性࿱…...
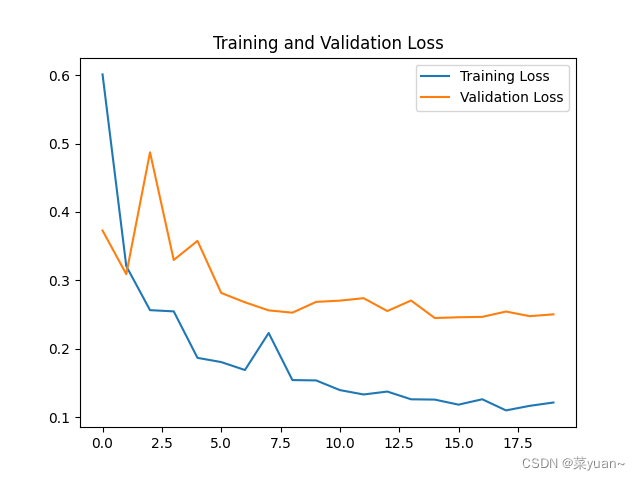
python与深度学习(十三):CNN和IKUN模型
目录 1. 说明2. IKUN模型2.1 导入相关库2.2 建立模型2.3 模型编译2.4 数据生成器2.5 模型训练2.6 模型保存2.7 模型训练结果的可视化 3. IKUN的CNN模型可视化结果图4. 完整代码 1. 说明 本篇文章是CNN的另外一个例子,IKUN模型,是自制数据集的例子。之前…...

题目:2283.判断一个数的数字计数是否等于数位的值
题目来源: leetcode题目,网址:2283. 判断一个数的数字计数是否等于数位的值 - 力扣(LeetCode) 解题思路: 两次遍历。第一次对字符串中每个出现的数字计数。第二次比较数字计数与数位的值是否相等。 解…...

任务14、无缝衔接,MidJourney瓷砖(Tile)参数制作精良贴图
14.1 任务概述 在这个实验任务中,我们将深入探索《Midjourney Ai绘画》中的Tile技术和其在艺术创作中的具有挑战性的应用。此任务将通过理论学习与实践操作相结合的方式,让参与者更好地理解Tile的核心概念,熟练掌握如何在Midjourney平台上使用Tile参数,并实际运用到AI绘画…...

【uniapp APP如何优化】
以下是一些可以进行优化的建议: 1. 减少网络请求次数:尽量避免在首页加载时请求大量数据,可以考虑使用分页加载,或者使用下拉刷新和上拉加载更多的方式。 2. 减小图片大小:使用压缩图片的工具,可以尽可能…...
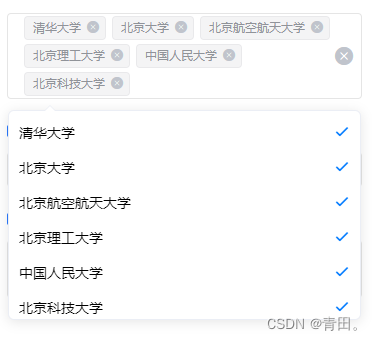
uni-app——下拉框多选
一、组件components/my-selectCheckbox.vue <template><view class"uni-stat__select"><span v-if"label" class"uni-label-text">{{label :}}</span><view class"uni-stat-box" :class"…...
从excel中提取嵌入式图片的解决方法
1 发现问题 我的excel中有浮动图片和嵌入式图片,但是openpyxl的_image对象只提取到了浮动图片,通过阅读其源码发现,这是因为openpyxl只解析了drawing文件导致的,所以确定需要自己解析 2 解决思路 1、解析出media资源 2、解析…...

python socket 网络编程的基本功
python socket逻辑思维整理 UDP发送步骤: 1 、先建立udp套接字 udp_socket socket.socket(socket.AF_INET, socket.SOCK_DGRAM) 2、利用sendto把数据并指定对端IP和端口,本端端口可以不用指定用自动随机的 udp_socket.sendto(“发送的内容”.encode(“…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...
