数据结构——搜索二叉树
文章目录
- 一. 概念
- 二. 二叉搜索树的操作
- 1.查找
- 2.插入
- 3.删除(重点)
- 4.遍历
- 5.拷贝构造与析构
- 三.二叉搜索树的递归实现
- 1.递归查找
- 2.递归插入
- 3.递归删除
- 四.二叉搜索树的性能分析
- 五.二叉树搜索的应用
- 六.源码
前言:
本章我们将认识一种新的二叉树——搜索二叉树。这棵树有个神奇的功能就是会对数据自动排序且有着非常高的查找效率。搜索二叉树作为set、map的基础结构,同样又是接下来将要学到的AVL树以及红黑树的实现基础非常值得我们去深入学习~
一. 概念
叉搜索树本质上也是一种二叉树,只不过多了一个约束规则——
若一棵二叉树不为空,则:
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为搜索二叉树
所以构建一个搜索二叉树,只需要在插入结点时满足约束规则即可。
二. 二叉搜索树的操作
与二叉树相同,二叉搜索树由一个个结点链接而成。每个结点包含三个成员——
template <class K>
struct BSTreeNode
{BSTreeNode<K>* _left; //左孩子BSTreeNode<K>* _right; //右孩子K _key; //键值BSTreeNode(const K& key):_left(nullptr), _right(nullptr), _key(key){}
};
所以再定义出BSTNode(Binary Search Tree简写)结构体——
template <class K>
class BSTree
{typedef BSTreeNode<K> Node;
public:// 成员函数的实现// 插入、删除、查找...
private:Node* _root = nullptr;
};
接着就是各种成员函数的实现了
1.查找
搜索二叉树的查找比较简单而且更容易帮助我们理解搜索二叉树的性质,所以先从查找入手。
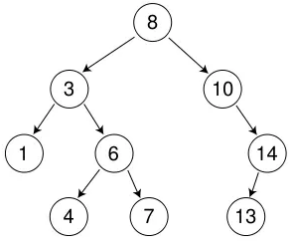
以上图为例,倘若我们要查找 7,具体的思路是这样的——
- 7 < 8,因此去 8 的左子树去查找
- 7 > 3,因此去 3 的右子树去查找
- 7 > 6,因此去 6 的右子树去查找
- 7 = 7,找到了,返回
true
于是我们试着着手实现一个Find函数
bool Find(const K& key)
{Node* cur = _root;while (cur){if (cur->_key < key) // 大于则去右子树查找cur = cur->_right;else if (cur->_key > key) // 小于则去左子树查找cur = cur->_left;elsereturn true; // 找到返回true}return false; // 未找到返回false
}
2.插入
理解了如何查找,插入也就非常简单。
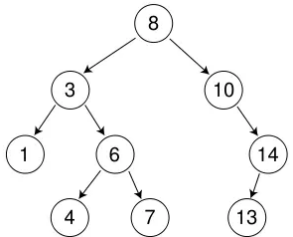
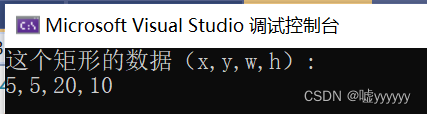
还是以此图为例,倘若我们要插入 9 ,具体步骤为——
- 首先确定
cur的位置,并随时更新parent - 最终,
cur走到10的左节点的位置,即cur = nullptr,循环结束 - 此时
patent = Node*(10) - 最后一步,
new一个结Node*(key)并赋值给parent->_left即可。
bool Insert(const K& key)
{// 如果是第一次插入,直接new一个新结点给_rootif (_root == nullptr){_root = new Node(key);return true;}Node* cur = _root; // cur用来定位插入的位置Node* parent = cur; // 记录parent的父亲while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if(cur->_key > key){parent = cur;cur = cur->_left;}else{return false;}}// 插入cur = new Node(key);// 插入时依旧要进行判断if (parent->_key < key)parent->_right = cur;elseparent->_left = cur;return true;
}
3.删除(重点)
二叉搜索树的删除是最精华的部分。对与叶子节点,例如4、7、13,删除非常简单,只需将自身的位置替换为nullptr即可。
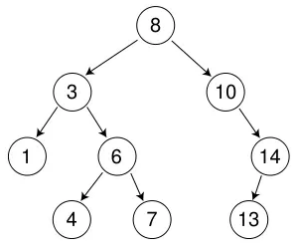
如果要删除14或者10,也是比较简单的,因为10的左右子树只有一方为nullptr(10的左子树为空),所以只需要载删除的时候让父结点接管自己不为空的子树即可。
倘若要删除6或者3,由于它们的左右子树都不为空,删除时无法将两个子树都交给父结点,情况就较为复杂。
所以此种情况,我们只能想办法请一个人来接替自己的位置,但是并不是谁来都能胜任这个位置的。这个接替者必须满足二叉搜索树的条件——左子树都比它小,右子树都比它大。那么这个接替者的人选只能有这两个——
- 左子树的最大(最右)节点
- 或右子树的最小(最左)节点
例如,倘若要删除3,此时有两种做法都可行——
- 用1替换3
- 用7替换3
综上所述,删除操作共分为一下几种情况——
- 左子树为空
- 右子树为空
- 左右子树都不为空
- (左右子树都为空其实可以归并到1或2的情况中)
bool Erase(const K& key)
{Node* cur = _root;Node* parent = cur;while (cur){// 找到值为key的结点if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else // 找到了{ // 删除if (cur->_left == nullptr) // 1.左子树为空{if (cur == _root) // 根节点的删除{_root = cur->_right;return true;}else{if (parent->_left == cur)parent->_left = cur->_right;elseparent->_right = cur->_right;delete cur;}}else if (cur->_right == nullptr) // 2.右子树为空{if (cur == _root) // 根节点的删除{_root = cur->_left;return true;}else{if (parent->_left == cur)parent->_left = cur->_left;elseparent->_right = cur->_left;delete cur;}}else // 左右子树都不为空{// 找左子树的最大结点 或者 右子树的最小结点Node* minRight = cur->_right;Node* pminRight = cur;while (minRight->_left){pminRight = minRight;minRight = minRight->_left;}cur->_key = minRight->_key; // 替换if (pminRight->_left == minRight){pminRight->_left = minRight->_right;}else{pminRight->_right = minRight->_right;}delete minRight;}return true;}}return false;
}
4.遍历
二叉搜索树的遍历非常简单,就是之前学习过的二叉树的中序遍历。
void InOrder()
{_InOrder(_root);cout << endl;
}void _InOrder(Node* root)
{if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << ' ';_InOrder(root->_right);
}
注:由于调用函数时C++封装的特性,需设计两个函数,InOrder接口对外提供,_InOrder不对外提供。
5.拷贝构造与析构
//采用前序遍历拷贝构造BSTree(const BSTree<K>& t){_root = _Copy(t._root);}Node* _Copy(Node* root){if (root ==nullptr){return nullptr;}Node* CopyRoot = new Node(root->_key);CopyRoot->_left = _Copy(root->_left);CopyRoot->_right = _Copy(root->_right);return CopyRoot;}//采用后序遍历的方式来删除,从下往上删。void _Destroy(Node*& root){if (root == nullptr){return;}_Destroy(root->_left);_Destroy(root->_right);delete root;root = nullptr;}~BSTree(){_Destroy(_root);}因为拷贝构造二叉搜索树时要保证树的结构与原来树的结构一致,因此采用前序遍历进行拷贝构造。
但如果写了拷贝构造之后编译器就不会生成默认的构造函数了,因为拷贝构造也属于构造,因此可以利用一下C++11的特性,强制编译器生成一个默认的拷贝构造
//强制编译器生成一个默认的拷贝构造
BSTree() = default;
三.二叉搜索树的递归实现
对于搜索二叉树来说,上面实现的非递归版本是比递归版本更优的。此处的递归实现完全属于多余了,但是作为拓展内容看一看也未尝不可。
1.递归查找
bool FindR(const K& key)
{return _FindR(_root, key);
}bool _FindR(Node* root, const K& key)
{if (root == nullptr)return false;if (root->_key == key)return true;if (root->_key > key)_FindR(root->_left, key);else_FindR(root->_right, key);
}
2.递归插入
bool InsertR(const K& key)
{return _EraseR(_root, key);
}bool _InsertR(Node*& root, const K& key)
{if (root == nullptr){root = new Node(key);return true;}if (root->_key < key)return _InsertR(root->_right, key);else if (root->_key > key)return _InsertR(root->_left, key);elsereturn false;
}
3.递归删除
bool EraseR(const K& key)
{return _EraseR(_root, key);
}bool _EraseR(Node*& root, const K& key)
{if (root == nullptr)return false;if (root->_key < key)return _EraseR(root->_right, key);else if(root->_key>key)return _EraseR(root->_left, key);else{Node* del = root;//1.右为空if (root->_right == nullptr)root = root->_left;//2.左为空else if (root->_left)root = root->_right;//3.左右都不为空else{//找左子树最大节点交换Node* maxleft = root->_left;while (maxleft->_right)maxleft = maxleft->_right;//找到后先交换要删除的值与左子树最大节点的值swap(root->_key, maxleft->_key);//再递归到左子树中去删除return _EraseR(root->_left, key);}delete del;return true;}
}
四.二叉搜索树的性能分析
插入和删除操作都必须先查找,查找效率代表了二叉搜索树中各个操作的性能。
对有n个结点的二叉搜索树,若每个元素查找的概率相等,则二叉搜索树平均查找长度是结点在二
叉搜索树的深度的函数,即结点越深,则比较次数越多。
但对于同一个关键码集合,如果各关键码插入的次序不同,可能得到不同结构的二叉搜索树:

- 最优情况下,二叉搜索树为完全二叉树(或者接近完全二叉树),其平均比较次数为: l o g 2 N log_2 N log2N
- 最差情况下,二叉搜索树退化为单支树(或者类似单支),其平均比较次数为: N 2 \frac{N}{2} 2N
如果退化成单支树,二叉搜索树的性能就失去了。那能否进行改进,不论按照什么次序插 入关键码,二叉搜索树的性能都能达到最优? 那么我们后续章节学习的AVL树和红黑树就可以上场了。
五.二叉树搜索的应用
K模型:K模型即只有key作为关键码,结构中只需要存储Key即可,关键码即为需要搜索到的值。
比如:给一个单词word,判断该单词是否拼写正确,具体方式如下:- 以词库中所有单词集合中的每个单词作为
key,构建一棵二叉搜索树 - 在二叉搜索树中检索该单词是否存在,存在则拼写正确,不存在则拼写错误。
- 以词库中所有单词集合中的每个单词作为
KV模型:每一个关键码key,都有与之对应的值Value,即<Key, Value>的键值对。该种方式在现实生活中非常常见:- 比如英汉词典就是英文与中文的对应关系,通过英文可以快速找到与其对应的中文,英文单词与其对应的中文
<word, chinese>就构成一种键值对 - 再比如统计单词次数,统计成功后,给定单词就可快速找到其出现的次数,单词与其出现次数就是
<word, count>就构成一种键值对
- 比如英汉词典就是英文与中文的对应关系,通过英文可以快速找到与其对应的中文,英文单词与其对应的中文
六.源码
namespace dianxia
{template <class K>struct BSTreeNode{BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;BSTreeNode(const K& key):_left(nullptr), _right(nullptr), _key(key){}};template <class K>class BSTree{typedef BSTreeNode<K> Node;public://强制编译器生成构造函数BSTree() = default;//拷贝构造BSTree(const BSTree<K>& t){_root = Copy(t._root);}//赋值重载BSTree<k>& operator=(BSTree<K> t){swap(_root, t._root);return *this;}~BSTree(){Destroy(_root);}//插入节点bool Insert(const K& key){//直接插入根if (_root == nullptr){_root = new Node(key);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{returen false;}}cur = new Node(key);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}bool Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{returen true;}}return false;}bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{//1.左为空if (cur->_left == nullptr){if (cur == _root){_root = cur->_right;}else{if (parent->_left == cur){parent->_left = cur->_right;}else{parent->_right == cur->_right;}}delete cur;}//2.右为空else if (cur->_right == nullptr){if (cur == _root){_root = cur->_left;}else{if (parent->_left == cur){parent->_left = cur->_left;}else{parent->_right == cur->_left;}}delete cur;}//3.左右都不为空,找右树最小节点或左树最大节点替代curelse{Node* pminRight = cur;Node* minRight = cur->_right;while (minRight->_left){pminRight = minRight;minRight = minRight->_left;}cur->_key = minRight->_key;if (pminRight->_left == minRight){pminRight->_left = minRight->_right;}else{pminRight->_right = minRight->_right;}delete minRight}return true;}}return false;}//递归版bool FindR(const K& key){return _FindR(_root, key);}bool InsertR(const K& key){return _InsertR(_root, key);}bool Erase(const K& key){return _Erase(_root, key);}bool Insorder(){_Insorder(_root);cout << endl;}protected:Node* Copy(Node* root){if (root == nullptr)return nullptr;Node* newRoot = new Node(root->_key);newRoot->_left = Copy(root->_left);newRoot->_right = Copy(root->_right);return newRoot;}void Destroy(Node*& root){if (root == nullptr)return;Destroy(root->_left);Destroy(root->_right);delete root;root = nullptr;}bool _FindR(Node* root, const K& key){if (root == nullptr)return false;if (root->_key == key)return true;if (root->_key < key)return _FindR(root->_right, key);else return _FindR(root->_left, key);}bool _InsertR(Node*& root, const K& key){if (root == nullptr){root = new Node(key);return true;}if (root->_key < key){return _InsertR(root->_right, key);}else if (root->_key > key){return _InsertR(root->_left, key);}else{return false;}}bool _EraseR(Node*& root, const K& key){if (root == nullptr)return false;if (root->_key < key)return _EraseR(root->_right, key);else if(root->_key>key)return _EraseR(root->_left, key);else{Node* del = root;//1.右为空if (root->_right == nullptr)root = root->_left;//2.左为空else if (root->_left)root = root->_right;//3.左右都不为空else{//找左子树最大节点交换Node* maxleft = root->_left;while (maxleft->_right)maxleft = maxleft->_right;//找到后先交换要删除的值与左子树最大节点的值swap(root->_key, maxleft->_key);//再递归到左子树中去删除return _EraseR(root->_left, key);}delete del;return true;}}private:Node* _root;};
}
本文到此结束,码文不易,还请多多支持!!!
相关文章:

数据结构——搜索二叉树
文章目录 一. 概念二. 二叉搜索树的操作1.查找2.插入3.删除(重点)4.遍历5.拷贝构造与析构 三.二叉搜索树的递归实现1.递归查找2.递归插入3.递归删除 四.二叉搜索树的性能分析五.二叉树搜索的应用六.源码 前言: 本章我们将认识一种新的二叉树—…...

3.3 Makefile的嵌套包含
一、Makefile包含子Makefile的示例 下面是一个示例Makefile和sub.mk的内容。 首先是sub.mk文件的内容: VAR := Hello from sub.mksay_hello:@echo $(VAR)然后是Makefile文件的内容: include sub.mkall: say_hellosay_hello:@echo "Hello from Makefile"在这个例…...

爬虫获取电影数据----以沈腾参演电影为例
数据可视化&分析实战 1.1 沈腾参演电影数据获取 文章目录 数据可视化&分析实战前言1. 网页分析2. 构建数据获取函数2.1 网页数据获取函数2.2 网页照片获取函数 3. 获取参演影视作品基本数据4. 电影详细数据获取4.1 导演、演员、描述、类型、投票人数、评分信息、电影海…...

网页版Java(Spring/Spring Boot/Spring MVC)五子棋项目(二)前后端实现用户的登录和注册功能【用户模块】
网页版Java五子棋项目(二)前后端实现用户的登录和注册功能【用户模块】 在用户模块我们要清楚要完成的任务一、MyBatis后端操作数据库1. 需要在数据库创建用户数据库1. 用户id2. 用户名3. 密码4. 天梯积分5. 总场数6. 获胜场数 2. 创建用户类User和数据库…...

2023年华数杯数学建模A题思路代码分析 - 隔热材料的结构优化控制研究
# 1 赛题 A 题 隔热材料的结构优化控制研究 新型隔热材料 A 具有优良的隔热特性,在航天、军工、石化、建筑、交通等 高科技领域中有着广泛的应用。 目前,由单根隔热材料 A 纤维编织成的织物,其热导率可以直接测出;但是 单根隔热…...
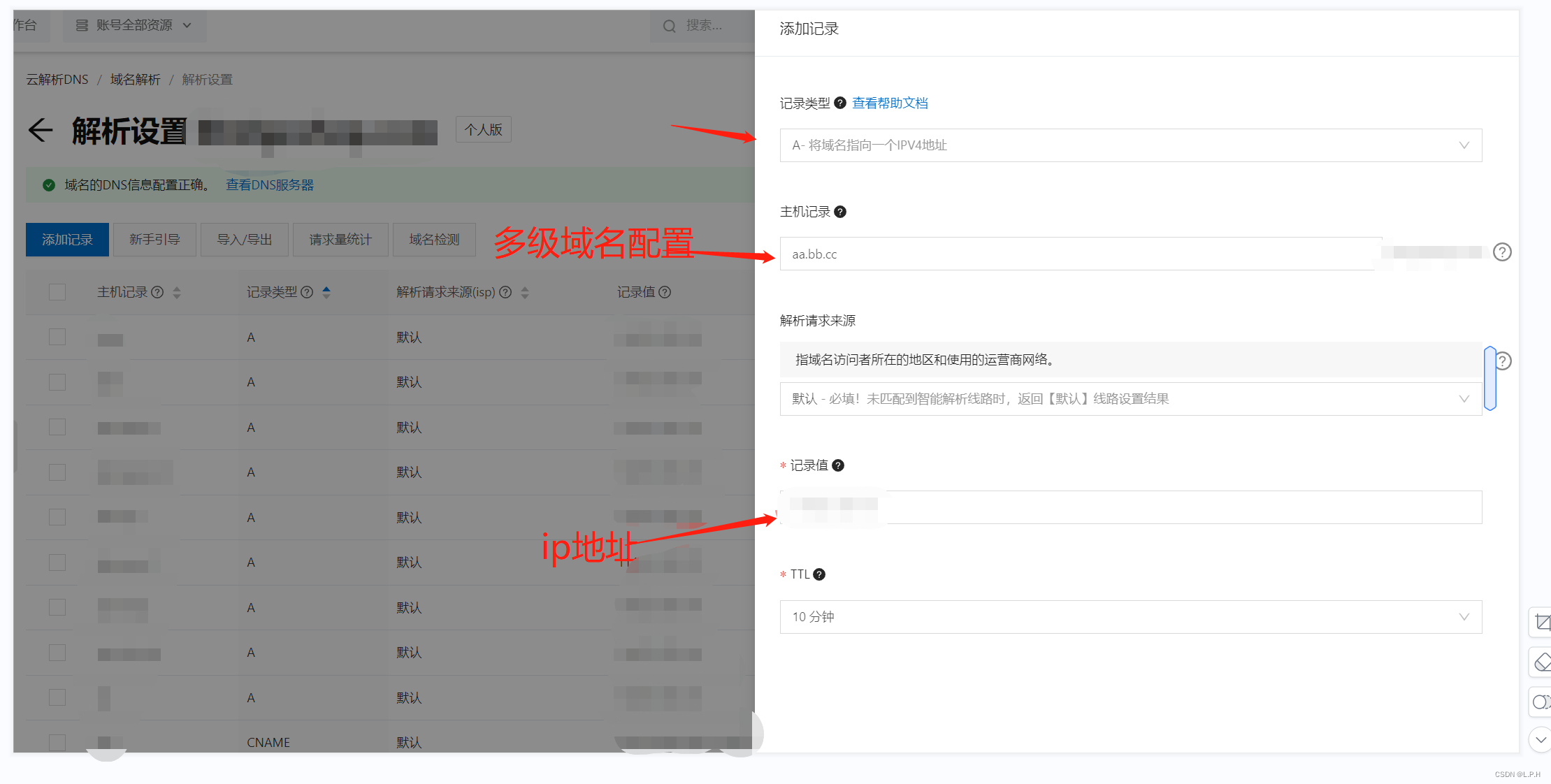
阿里云二级域名配置
阿里云二级域名配置 首先需要进入阿里云控制台的域名管理 1.选择域名点击解析 2.添加记录 3.选择A类型 4.主机记录设置【可以aa.bb或者aa.bb.cc】 到时候会变成:aa.bb.***.com 5.解析请求来源设置为默认 6.记录值 设置为要解析的服务器的ip地址 7.TTL 默认即…...

Webpack5 动态导入按需加载
文章目录 一、 什么是动态导入和按需加载?二、 具体用法示例二、 总结 一、 什么是动态导入和按需加载? 传统上,在Webpack中,我们使用import语句可以在代码中静态地导入模块。这意味着所有的模块都会在构建时被打包到bundle中。然…...

【Linux操作系统】Ubuntu和center两个Linux发行版本中指令的区别
Ubuntu和center是Linux的两个发行版本,本文将详细介绍两个发行版的使用命令区别,分析两者的优缺点。 文章目录 常见的区别:细节差异:两个发行版本各自的优点和缺点Ubuntu 的优点:Ubuntu 的缺点:CentOS 的优…...
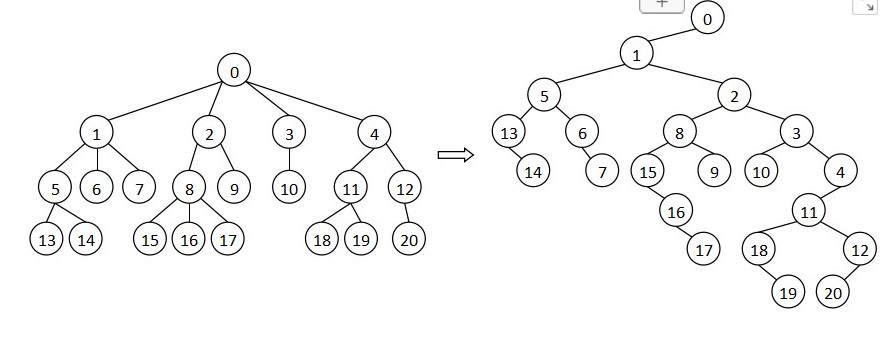
c++基本数据结构
void insert(const node *head, node *p) {node *x, *y;yhead;do{xy;yx->next;} while ((y!NULL) && (y->value < p->value);x->nextp;p->nexty; } 二.栈 (1) 栈的实现! 操作规则:先进后出,先出后进。 int stack[N], top0; /…...
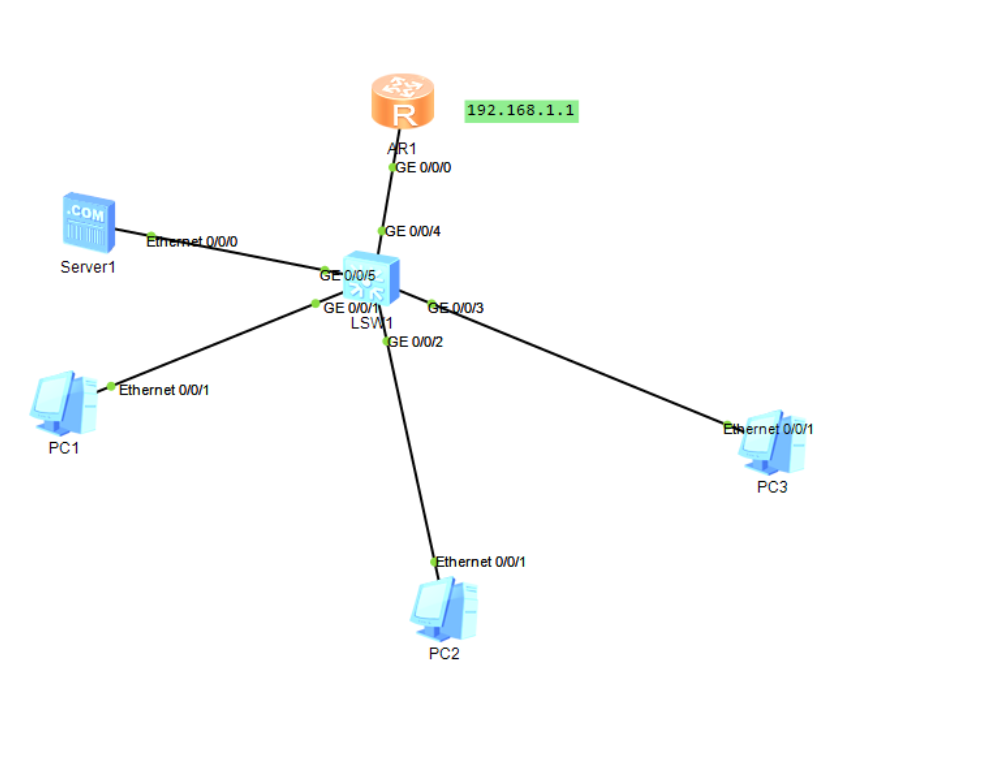
路由器DHCP实验
拓扑图 配置 # 配置ip地址并开启dhcp [Huawei]int g0/0/0 [Huawei-GigabitEthernet0/0/0]ip addr 192.168.1.1 255.255.255.0 [Huawei-GigabitEthernet0/0/0]dhcp enable## 配置dns地址 [Huawei-GigabitEthernet0/0/0]dhcp dns-list 192.168.1.5## 指定某个接口开通DHCP 功能…...

Linux 电源子系统之充电、放电、低功耗
在嵌入式产品中,有三个重要模块:充电、放电、低功耗。 1、充电 charging 1、开关电源基本原理 2、线性充电和开关电源硬件电路图分析 3、Battery_Charging_v1.2 spec 4、typec spec 5、typec-PD spec 6、Uevent 在 Android 层的实现 7、battery service 监听 uevent 事件以…...

捕捉时刻:将PDF文件中的图像提取为个性化的瑰宝(从pdf提取图像)
应用场景: 该功能的用途是从PDF文件中提取图像。这在以下情况下可能会很有用: 图片提取和转换:可能需要将PDF文件中的图像提取出来,并保存为单独的图像文件,以便在其他应用程序中使用或进行进一步处理。例如ÿ…...

【基础类】—HTTP协议类
一、HTTP协议的主要特点 简单快速:每个资源URI是固定的,访问某个资源输入URI即可灵活:在每一个HTTP协议中,请求头部分有一个数据类型,通过一个HTTP协议可以完成不同的数据类型传输无连接:连接一次就会断开…...

【Qt高级】QThread与QTimer组合使用引出的信号槽执行在哪个线程的思考【2023.08.06】
源码见 testQThread_QTimer… Qt 版本5.6.3 视频讲解:https://www.bilibili.com/video/BV15P411C79i/ 链接: 视频讲解 简介 想法很单纯,就是主线程启动一个子线程,子线程里启动一个定时器,定时执行一些任务,然鹅实际开…...
用于大型图像模型的 CNN 内核的最新内容
一、说明 由于OpenAI的ChatGPT的巨大成功引发了大语言模型的繁荣,许多人预见到大图像模型的下一个突破。在这个领域,可以提示视觉模型分析甚至生成图像和视频,其方式类似于我们目前提示 ChatGPT 的方式。 用于大型图像模型的最新深度学习方法…...

索尼电视怎么完全关机
索尼电视怎么完全关机 当用户想要关闭索尼电视时,可能会遇到一些问题。例如,他们可能会遇到如何完全关闭电视的问题。在本文中,我们将介绍如何完全关闭索尼电视。 首先,您需要找到索尼电视的电源按钮。通常,该按钮位…...
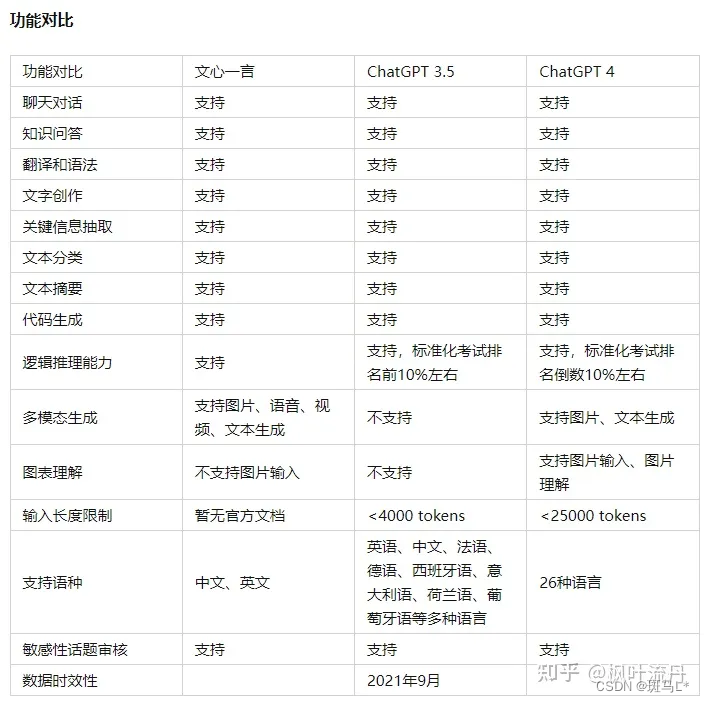
AI介绍——chat gpt/文心一言/claude/bard/星火大模型/bing AI
AI体验 1. AI 介绍(注册和使用)1.1 Chat GPT1.2 文心一言1.3 Slack 上的 Claude1.3.1 Claude 介绍1.3.2 Claude 使用 1.4 Google的Bard1.4.1 Bard 介绍1.4.2 Bard 使用 1.5 科大讯飞的星火大模型1.5.1 星火大模型 介绍1.5.2 星火大模型 使用 1.6 new bin…...
C++ 访问控制——公有继承、私有继承、保护继承
派生类继承了基类的全部数据成员和除了构造函数和析构函数之外的全部函数成员,但是这些成员的访问属性在派生的过程中是可以调整的。从基类继承的成员,其访问属性由继承方式控制。 基类的成员有public(公有)、protectedÿ…...

python性能调试
py-spy生成cpu火焰图 ft5.svg env/xxxx/bin pid26443$env/py-spy record -o /tmp/$f --pid $pid --nativememray实时查看内存 env/xxxx/bin$env/python -m memray run --live --trace-python-allocators --native run_demo.pymemray生成内存火焰图报告 frun_demo_042.bin en…...

738. 单调递增的数字
738. 单调递增的数字 当且仅当每个相邻位数上的数字 x 和 y 满足 x < y 时,我们称这个整数是单调递增的。 给定一个整数 n ,返回 小于或等于 n 的最大数字,且数字呈 单调递增 。 示例 1: 输入: n 10 输出: 9示例 2: 输入: n 1234 输出…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...
