数据结构——红黑树
文章目录
- 一.红黑树的定义
- 二.红黑树的插入
- 1.红黑树节点的定义
- 2.红黑树的插入操作
- 3.总结:
- 三.红黑树与AVL树的比较
- 四.检验手写的红黑树
- 五.源码
一.红黑树的定义
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是
Red或Black。通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的。
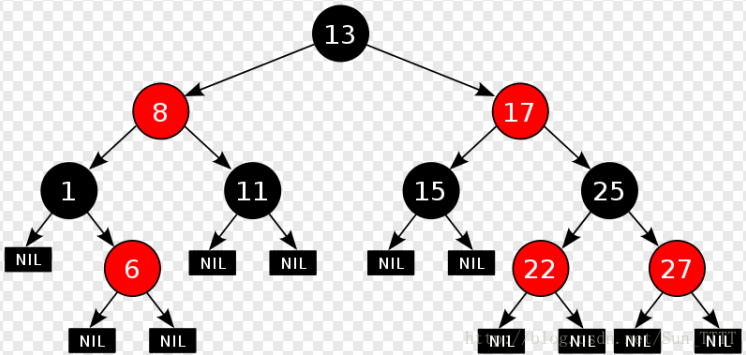
红黑树的性质:
- 每个结点不是红色就是黑色
- 根节点是黑色的
- 如果一个节点是红色的,则它的两个孩子结点是黑色的
- 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均 包含相同数目的黑色结点
- 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)
解读:
性质三:保证树中没有连续的红色节点
性质四:每条路径上黑色节点的数目相同
满足以上性质,红黑树就能保证:其最长路径中节点个数不会超过最短路径节点个数的两倍
其中,其极限最短:全黑。极限最长:一黑一红……
可以发现,最坏情况的时间复杂度和AVL树一样,都是O(logN),但是红黑树这种近似平衡的结构减少了大量旋转,综合性能优于AVL树。
二.红黑树的插入
1.红黑树节点的定义
enum Colour
{Red,Black
};template<class K, class V>
struct RBTreeNode
{RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;pair<K, V> _kv;Colour _col;RBTreeNode():_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv){}
};
2.红黑树的插入操作
插入步骤:
-
按照二叉搜索的树规则插入新节点
-
检测新节点插入后,红黑树的性质是否造到破坏
-
因为新节点的默认颜色是红色,因此:如果其双亲节点的颜色是黑色,没有违反红黑树任何性质,则不需要调整;但当新插入节点的双亲节点颜色为红色时,就违反了性质三不能有连在一起的红色节点,此时需要对红黑树分情况来讨论:
约定:cur为当前节点,p为父节点,g为祖父节点,u为叔叔节点-
情况一:
cur为红,p为红,g为黑,u存在且为红
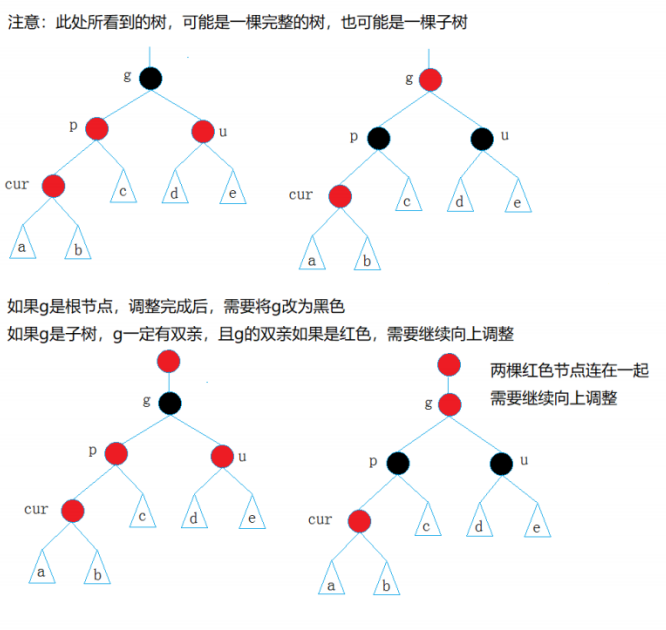
解决方式:将p,u改为黑,g改为红,然后把g当成cur,继续向上调整 -
情况二:
cur为红,p为红,g为黑,u不存在/u存在且为黑
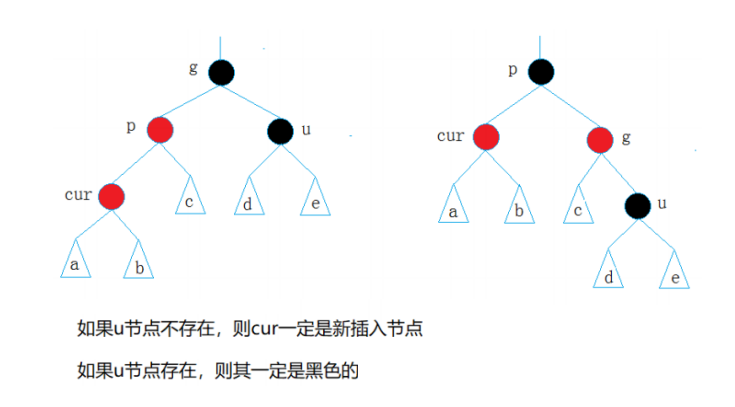
解决方式:
p为g的左孩子,cur为p的左孩子,则进行右单旋转;相反,p为g的右孩子,cur为p的右孩子,则进行左单旋转。p、g变色–p变黑,g变红- 情况三:
cur为红,p为红,g为黑,u不存在/u存在且为黑
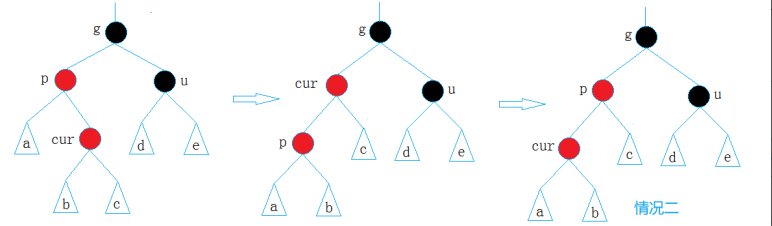
解决方式:p为g的左孩子,cur为p的右孩子,则针对p做左单旋转;相反,p为g的右孩子,cur为p的左孩子,则针对p做右单旋转
-
3.总结:
插入新节点时,父节点为红,看叔叔的颜色。
- 叔叔存在且为红,变色,向上调整(可能变为三种情况中的任意一种)
- 叔叔不存在/存在且为黑,直线。单旋+变色
- 叔叔不存在/存在且为黑,折线,两次单旋+变色
三.红黑树与AVL树的比较
红黑树和AVL树都是高效的平衡二叉树,增删改查的时间复杂度都是O( l o g 2 N log_2 N log2N)
红黑树不追求绝对平衡,其只需保证最长路径不超过最短路径的2倍,相对而言,降低了插入和旋转的次数,所以在经常进行增删的结构中性能比AVL树更优,而且红黑树实现比较简单,所以实际运用中红黑树更多。
四.检验手写的红黑树
//检查有没有连续红节点
bool Check(Node* root,int blackNum,const int ref)
{if (root == nullptr){if (blackNum != ref){cout << "路径上黑节点数量不一致" << endl;return false;}return true;}if (root->_col == BLACK){++blackNum;}if (root->_col == RED && root->_parent->_col == RED){cout << "违反规则,父子均为红" << endl;return false;}return Check(root->_left, blackNum,ref) && Check(root->_right, blackNum, ref);
}
//统计某条路径的黑色节点数量,然后计算所有路径的黑色节点数量与该路径比对
bool _IsBalance()
{if (_root == nullptr)return true;if (_root->_col != BLACK){return false;}int ref = 0;Node* left = _root;while (left != nullptr){if (left->_col == BLACK){++ref;}left = left->_left;}return Check(_root,0,ref);
}
五.源码
namespace dianxia
{enum Colour{Red,Black};template<class K,class V>struct RBTreeNode{RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;pair<K, V> _kv;Colour _col; //节点颜色RBTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv){}};template<class K,class V>class RBTree{typedef RBTreeNode<K,V> Node;public:bool Insert(const pair<K, V>& kv){//直接插入根节点if (_root == nullptr){_root = new Node(kv);_root->_col = Black;return true;}Node* parent = nullptr;Node* cur = _root;while(cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}//找到新结点cur = new Node(kv);cur->_col = Red;//连接节点if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;//检查是否满足红黑树的要求while (parent && parent->_col == Red){//p为红则gp一定存在且为黑Node* grandparent = parent->_parent;assert(grandparent);assert(grandparent->_col==Black);if (parent == grandparent->_left){Node* uncle = grandparent->_right;//1.u存在且为红,变色并继续向上更新if (uncle && uncle->_col == Red){parent->_col = uncle->_col = Black;grandparent->_col = Red;cur = grandparent;parent = cur->_parent;}//2.u不存在或u为黑 变色加旋转else{if (cur == parent->_left){// g// p u// c//右旋RotateR(grandparent);parent->_col = Black;grandparent->_col = Red;}else{// g// p u// c//先左旋再右旋RotateL(parent);RotateR(grandparent);cur->_col = Black;grandparent->_col = Red;}break;}}else //grandparent->_right==parent{Node* uncle = grandparent->_left;//1.u存在且为红,变色并继续向上更新if (uncle && uncle->_col == Red){parent->_col = uncle->_col = Black;grandparent->_col = Red;cur = grandparent;parent = cur->_parent;}//2.u不存在或u为黑 变色加旋转else{if (cur == parent->_right){// g// u p// c//左RotateL(grandparent);parent->_col = Black;grandparent->_col = Red;}else{// g// u p// c//先右旋再左旋RotateR(parent);RotateL(grandparent);cur->_col = Black;grandparent->_col = Red;}break;}}}_root->_col = Black;return true;}~RBTree(){_Destroy(_root);_root = nullptr;}void Inorder(){_InOrder(_root);}//检查红黑树:1.检查以根节点为根的每条路径黑色节点的数目是否都相等// 2.检查某条路径上是否有连续的红色节点bool Isbalance(){if (_root && _root->_col == Red){cout << "根节点是红色的" << endl;return false;}int benchmark = 0;Node* cur = _root;while (cur){if (cur->_col == Black)++benchmark;cur = cur->_left;}return _Check(_root, 0, benchmark);}int Height(){return _Height(_root);}private:void _Destroy(Node* root){if (root == nullptr){return;}_Destroy(root->_left);_Destroy(root->_right);delete root;}int _Height(Node* root){if (root == nullptr)return 0;int leftH = _Height(root->_left);int rightH = _Height(root->_right);return leftH > rightH ? leftH + 1 : rightH + 1;}void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_kv.first << " ";_InOrder(root->_right);}bool _Check(Node* root, int blacknum, int benchmark){if (root == nullptr){if (benchmark != blacknum){cout << "某条路径黑色节点的数量不相等" << endl;return false;}return true;}if (root->_col == Black)++blacknum;if (root->_col == Red && root->_parent && root->_parent->_col == Red){cout << "某条路径存在连续的红色节点" << endl;return false;}return _Check(root->_left, blacknum, benchmark)&& _Check(root->_right, blacknum, benchmark);}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;Node* ppnode = parent->_parent;subR->_left = parent;parent->_parent = subR;if (ppnode == nullptr){_root = subR;_root->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subR;}else{ppnode->_right = subR;}subR->_parent = ppnode;}}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* ppnode = parent->_parent;subL->_right = parent;parent->_parent = subL;if (parent == _root){_root = subL;_root->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subL;}else{ppnode->_right = subL;}subL->_parent = ppnode;}}private:Node* _root = nullptr;};
}
本文到此结束,码文不易,还请多多支持!!
相关文章:

数据结构——红黑树
文章目录 一.红黑树的定义二.红黑树的插入1.红黑树节点的定义2.红黑树的插入操作3.总结: 三.红黑树与AVL树的比较四.检验手写的红黑树五.源码 一.红黑树的定义 红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色ÿ…...

【C++】数据结构与算法:常用排序算法
😏★,:.☆( ̄▽ ̄)/$:.★ 😏 这篇文章主要介绍常用排序算法。 学其所用,用其所学。——梁启超 欢迎来到我的博客,一起学习,共同进步。 喜欢的朋友可以关注一下,下次更新不迷路…...

【C++】Bullet3代码存档
之前试了一下Bullet3物理引擎,但在linux上编译失败,于是放弃了。令我不满的还有另外一个原因,下载的发行包竟然有500M。C的Bullet3代码根本用不了,大部分教程实际都是用的老版本。而且此项目还整了python版本,各种蹭人…...

弘扬“两弹一星”精神,勇攀科学技术高峰——道本科技商业大学党日活动圆满落幕
2023年8月2日,道本科技与商业大学携手举办了一场主题为“弘扬‘两弹一星’精神,勇攀科学技术高峰”的党日活动。本次活动旨在了解党领导下的中国核工业发展历程,传承和弘扬“两弹一星”精神,同时展示道本科技创新产品,…...

Java中创建对象的几种方式
背景 面试的时候有些面试官喜欢问这些, 这里简单记录一下. 常见方式 方式1: new XXXX(); 使用new关键字:这是最常见的创建对象的方式,使用new关键字后面跟上类名和参数列表(如果有),可以调用类的构造方法来创建对象…...

Python(三)
诚信像一面镜子,一旦打破,你的人格就会出现裂痕。 存在短路的情景 谢谢观看 Python(三)...

android 如何分析应用的内存(十五)——Visual Studio Code 调试Android应用
android 如何分析应用的内存(十五)——Visual Studio Code 调试Android 应用 在上一篇文章介绍了jdb调试java应用 接下来介绍用UI界面调试java应用,达到同jdb一样的效果。 同样的UI界面有很多选择,如Eclipse,Android …...

宁波银行最新内推码 MK4913
宁波银行最新内推码 MK4913 内推码: MK4913 内推二维码 : 网申路径: 网页端:登录宁波银行招聘官网: https://zhaopin.nbcb.com.cn 选择【校园招聘】-【招聘岗位】手机端:关注【宁波银行招聘】公众号&a…...
postgresql|数据库|MySQL数据库向postgresql数据库迁移的工具pgloader的部署和初步使用
前言: MySQL数据库和postgresql数据库之间的差异并不多,这里的差异指的是对SQL语言的支持两者并不大,但底层的东西差异是非常多的,例如,MySQL的innodb引擎概念,数据库用户管理,这些和postgresq…...

【Python从小白到高手】---函数基础
个人主页:平行线也会相交 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 平行线也会相交 原创 收录于专栏【Python小白从入门到精通】🎈 本专栏旨在分享学习Python的一点学习心得,欢迎大家在评论区讨论💌 目录…...
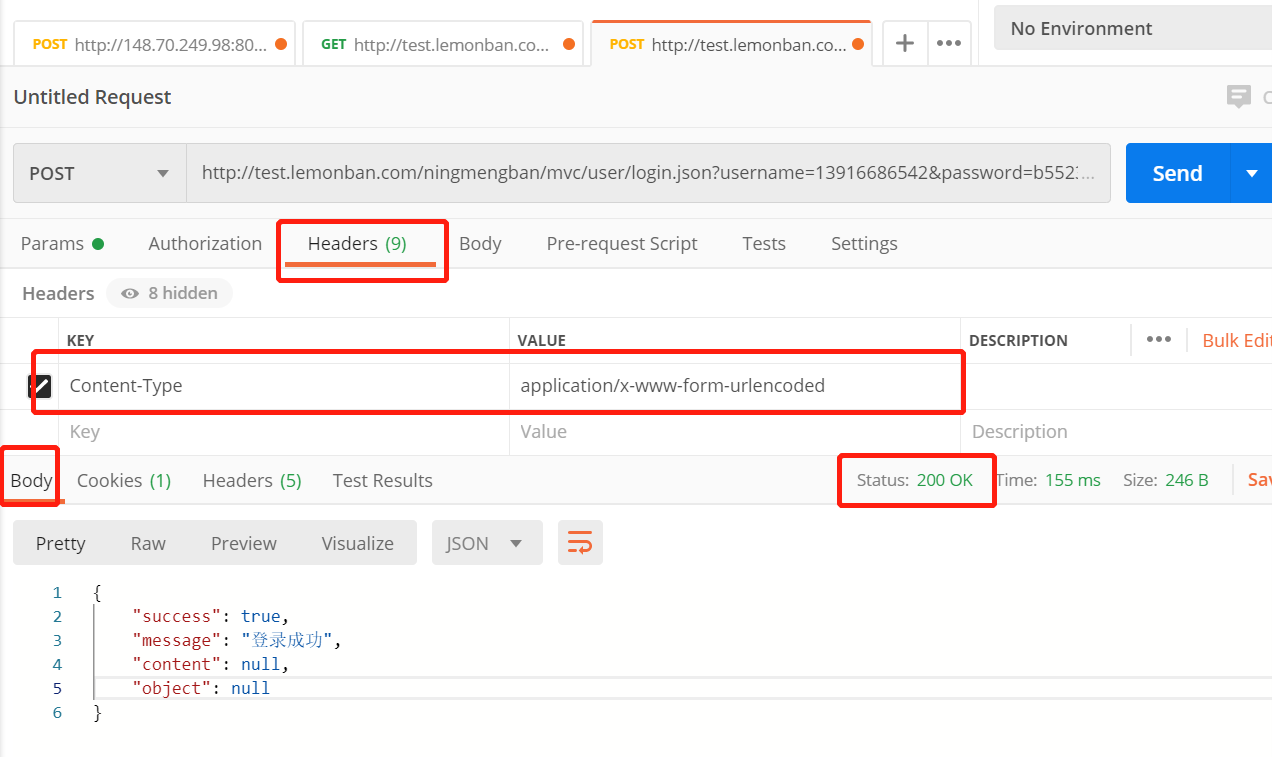
postman----传参格式(json格式、表单格式)
本文主要讲解postman使用post请求方法的2中传参方式:json格式、表单格式 首先了解下,postman进行接口测试,必须条件是: ♥请求地址 ♥请求协议 ♥请求方式 ♥请求头 ♥参数 json格式 先看一下接口文档,根据接口文档&…...
Uni-Dock:GPU 分子对接使用教程
github文件下载: git clone https://github.com/dptech-corp/Uni-Dock.git cd Uni-Dock/example/screening_test wget https://github.com/dptech-corp/Uni-Dock/releases/download/1.0.0/unidock 将此文件加入到全局变量中 chmod x unidock sudo mv unidock /…...
【Python】数据分析+数据挖掘——掌握Python和Pandas中的单元格替换操作
1. 前言 数据处理和清洗是数据分析和机器学习中至关重要的步骤。在数据处理过程中,我们经常需要对数据集进行清洗和转换,其中单元格替换是一个常用的技术。Python作为一种功能强大且灵活的编程语言,为数据处理提供了丰富的工具和库。Pandas库…...

Godot 4 源码分析 - 增加格式化字符串功能
Godot 4的主要字符串类型为String,已经设计得比较完善了,但有一个问题,格式化这块没怎么考虑。 String中有一个format函数,但这个函数只有两个参数,这咋用? String String::format(const Variant &va…...
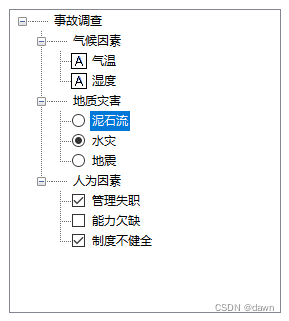
C#中XML文档与Treeview控件操作的数据同步
在前文《C#使用XML和Treeview结合实现复杂数据采集功能》中,使用Treeview展示了XML的数据,问题是如果在Treeview上进行了操作,怎样同步更改XML数据的内容呢? 这个问题看似简单,实现起来有一点小麻烦。 要实现的操作功能…...
【Java Web基础】mvn命令、Maven的安装与配置
本文极大程度上来自Maven安装(超详解),但是担心安的过程中遇到什么不一样的问题,顺便加深印象,所以还是打算自己弄一篇。 目录 第一步:Download Maven第二步:解压与安装2.1 解压2.2 安装 第一步:Download …...
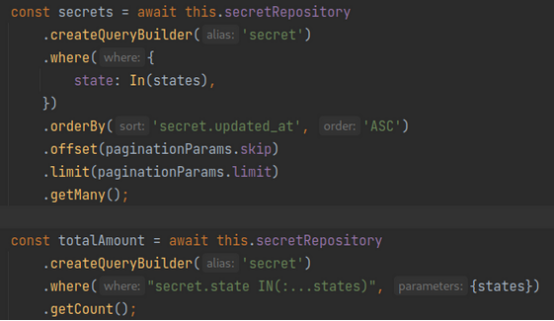
加强Web应用程序安全:防止SQL注入
数据库在Web应用程序中存储和组织数据时起着至关重要的作用,它是存储用户信息、内容和其他应用程序数据的中央存储库。而数据库实现了高效的数据检索、操作和管理,使Web应用程序能够向用户提供动态和个性化的内容。然而,数据库和网络应用程序…...

【云原生】k8s中Contrainer 生命周期回调/策略/指针学习
个人主页:征服bug-CSDN博客 kubernetes专栏:kubernetes_征服bug的博客-CSDN博客 目录 1 容器生命周期 2 容器生命周期回调/事件/钩子 3 容器重启策略 4 自定义容器启动命令 5 容器探针 1 容器生命周期 Kubernetes 会跟踪 Pod 中每个容器的状态&am…...
electron+vue3全家桶+vite项目搭建【25】使用electron-updater自动更新应用
文章目录 引入实现效果实现步骤引入依赖配置electron-buidler文件封装版本升级工具类主进程调用版本更新校验渲染进程封装方法调用 测试版本更新 引入 demo项目地址 electron-updater官网 我们不可能每次发布新的版本都让用户去手动下载安装最新的包,而是应用可以…...
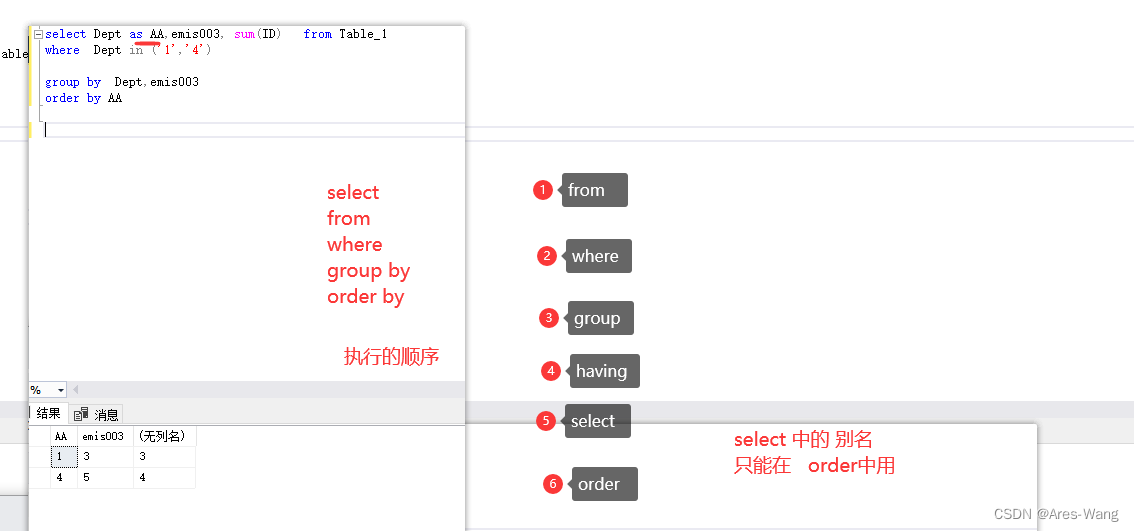
SQL 表别名 和 列别名
列表名 列表名之后 order by 可以用别名 也可以用原名, where 中不能用别名的 SQL语句执行顺序: from–>where–>group by -->having — >select --> order 第一步:from语句,选择要操作的表。 第二步࿱…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...
