POJ 3169 Layout BellmanFord Dijkstra
一、心路历程
这一个题目写了三天,可以说是非常挣扎了,明明是例题,但是就是倔强着不去看书上的题解,WA了7次,TLE了4次。
写了不知道多少条测试用例,一遍一遍的过,一点一点的调试。

最后终于找到了规则
二、思路
1、题目要求1到N,必须按照顺序排,那么我们就可以认为 对每个 i >1,存在 i -1 到 i 的 0 的斥力
2、我们每一条A到B的排斥力P,看作B到A引力力 P * (-1)
3、规则1中 斥力,和 输入的斥力,都按照第二条规则,转化引力,然后不考虑斥力
4、用 BellmanFord算法,对转换成的和输入的引力集合,判断是否存在负圈,存在直接输出-1
5、不存在负圈,则直接对转换成的和输入的引力集合使用dijkstra算法,起点是1,如果d[N]大于1000000007(每条边最大值乘以边数,加7是为了防止边界出错),则输出-2,否则输出d[N]。
三、代码
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
struct Node
{int from, to, cost;Node(int from = 0, int to = 0, int cost = 0) : from(from), to(to), cost(cost) {}
};
vector<Node> nodes;
typedef pair<int, int> P;
vector<P> edges[1007];
int d[1007], N, inf = 0x3f3f3f3f, ML, MD, area[1007][1007];
bool used[1007];
void input()
{int from, to, cost;for (int i = 1; i <= ML; i++){scanf("%d%d%d", &from, &to, &cost);edges[from].push_back(P(cost, to));nodes.push_back(Node(from, to, cost));}for (int i = 1; i <= MD; i++){scanf("%d%d%d", &from, &to, &cost);edges[to].push_back(P(-cost, from));nodes.push_back(Node(to, from, -cost));}for (int i = 2; i <= N; i++){edges[i].push_back(P(0, i - 1));nodes.push_back(Node(i, i - 1, -1));}
}
bool bellmanFord(int s)
{bool flag = false;for (int i = 1; i <= N; i++){d[i] = inf;}d[s] = 0;for (int i = 1; i <= N; i++){for (int j = 0; j < nodes.size(); j++){if (d[nodes[j].from] + nodes[j].cost < d[nodes[j].to]){d[nodes[j].to] = d[nodes[j].from] + nodes[j].cost;if (i == N){flag = true;}}}}return flag;
}
void dijkstra(int s)
{for (int i = 1; i <= N; i++){d[i] = inf;used[i] = false;}d[s] = 0;priority_queue<P, vector<P>, greater<P>> que;que.push(P(0, s));while (!que.empty()){P current = que.top();que.pop();if (used[current.second] || current.first > d[current.second]){continue;}for (int i = 0; i < edges[current.second].size(); i++){P toEdge = edges[current.second][i];if (d[current.second] + toEdge.first < d[toEdge.second]){d[toEdge.second] = toEdge.first + d[current.second];que.push(P(d[toEdge.second], toEdge.second));}}}
}
void solve()
{if (bellmanFord(1)){printf("%d\n", -1);}else{dijkstra(1);if (d[N] > 1000000007){printf("%d\n", -2);}else{printf("%d\n", d[N]);}}
}
int main()
{scanf("%d%d%d", &N, &ML, &MD);input();solve();return 0;
}
相关文章:

POJ 3169 Layout BellmanFord Dijkstra
一、心路历程 这一个题目写了三天,可以说是非常挣扎了,明明是例题,但是就是倔强着不去看书上的题解,WA了7次,TLE了4次。 写了不知道多少条测试用例,一遍一遍的过,一点一点的调试。 最后终于找到…...

数据库管理员知识图谱
初入职场的程序猿,需要为自己做好职业规划,在职场的赛道上,需要保持学习,并不断点亮自己的技能树。 成为一名DBA需要掌握什么技能呢,先让Chat-GPT为我们回答一下: 数据库管理系统 (DBMS)知识ÿ…...

中兴服务器支持百度“文心一言”,助力AI产业发展
前段时间,中兴和百度正式对外宣布中兴服务器将会支持百度“文心一言”,为其提供更加强劲的算力支撑,从而加速“文心一言”的完事升级与更新迭代,助力AI产业化应用和生态的繁荣发展。 “文心一言”是百度基于文心大模型技术推出…...

STM 如何通过网络 time.windows.com获取时间
STM 如何通过网络 time.windows.com获取时间 在STM32中,你可以使用STM32Cube HAL库提供的网络套接字API来通过网络获取时间。以下是一个示例代码,演示如何通过time.windows.com获取时间: #include "stm32xxxx.h" #include "lwip/sockets.h" #include …...
数据结构——红黑树
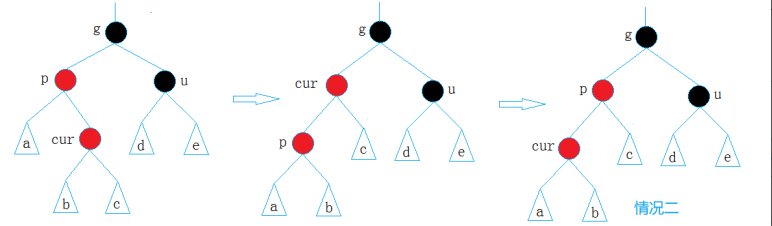
文章目录 一.红黑树的定义二.红黑树的插入1.红黑树节点的定义2.红黑树的插入操作3.总结: 三.红黑树与AVL树的比较四.检验手写的红黑树五.源码 一.红黑树的定义 红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色ÿ…...

【C++】数据结构与算法:常用排序算法
😏★,:.☆( ̄▽ ̄)/$:.★ 😏 这篇文章主要介绍常用排序算法。 学其所用,用其所学。——梁启超 欢迎来到我的博客,一起学习,共同进步。 喜欢的朋友可以关注一下,下次更新不迷路…...

【C++】Bullet3代码存档
之前试了一下Bullet3物理引擎,但在linux上编译失败,于是放弃了。令我不满的还有另外一个原因,下载的发行包竟然有500M。C的Bullet3代码根本用不了,大部分教程实际都是用的老版本。而且此项目还整了python版本,各种蹭人…...

弘扬“两弹一星”精神,勇攀科学技术高峰——道本科技商业大学党日活动圆满落幕
2023年8月2日,道本科技与商业大学携手举办了一场主题为“弘扬‘两弹一星’精神,勇攀科学技术高峰”的党日活动。本次活动旨在了解党领导下的中国核工业发展历程,传承和弘扬“两弹一星”精神,同时展示道本科技创新产品,…...

Java中创建对象的几种方式
背景 面试的时候有些面试官喜欢问这些, 这里简单记录一下. 常见方式 方式1: new XXXX(); 使用new关键字:这是最常见的创建对象的方式,使用new关键字后面跟上类名和参数列表(如果有),可以调用类的构造方法来创建对象…...

Python(三)
诚信像一面镜子,一旦打破,你的人格就会出现裂痕。 存在短路的情景 谢谢观看 Python(三)...

android 如何分析应用的内存(十五)——Visual Studio Code 调试Android应用
android 如何分析应用的内存(十五)——Visual Studio Code 调试Android 应用 在上一篇文章介绍了jdb调试java应用 接下来介绍用UI界面调试java应用,达到同jdb一样的效果。 同样的UI界面有很多选择,如Eclipse,Android …...

宁波银行最新内推码 MK4913
宁波银行最新内推码 MK4913 内推码: MK4913 内推二维码 : 网申路径: 网页端:登录宁波银行招聘官网: https://zhaopin.nbcb.com.cn 选择【校园招聘】-【招聘岗位】手机端:关注【宁波银行招聘】公众号&a…...
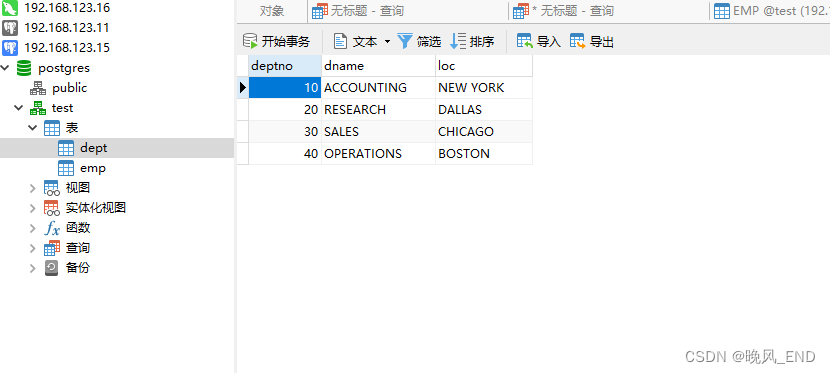
postgresql|数据库|MySQL数据库向postgresql数据库迁移的工具pgloader的部署和初步使用
前言: MySQL数据库和postgresql数据库之间的差异并不多,这里的差异指的是对SQL语言的支持两者并不大,但底层的东西差异是非常多的,例如,MySQL的innodb引擎概念,数据库用户管理,这些和postgresq…...

【Python从小白到高手】---函数基础
个人主页:平行线也会相交 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 平行线也会相交 原创 收录于专栏【Python小白从入门到精通】🎈 本专栏旨在分享学习Python的一点学习心得,欢迎大家在评论区讨论💌 目录…...
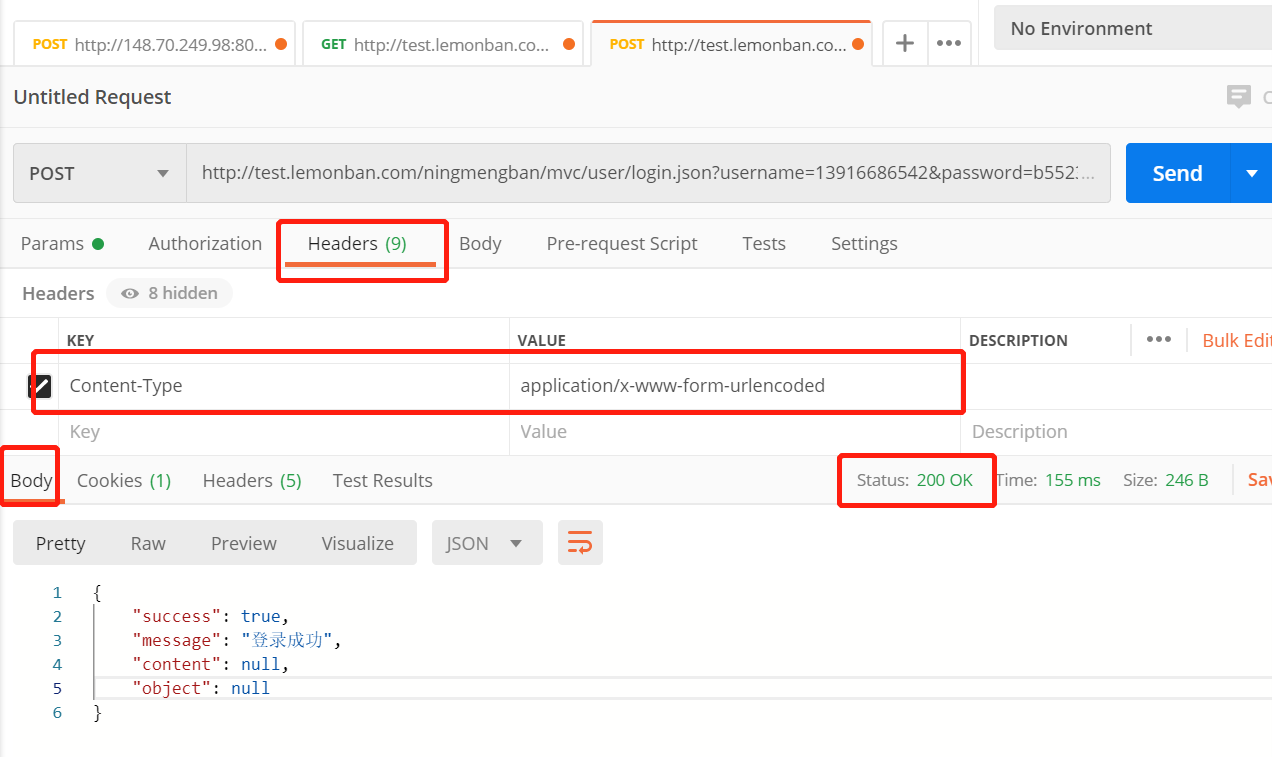
postman----传参格式(json格式、表单格式)
本文主要讲解postman使用post请求方法的2中传参方式:json格式、表单格式 首先了解下,postman进行接口测试,必须条件是: ♥请求地址 ♥请求协议 ♥请求方式 ♥请求头 ♥参数 json格式 先看一下接口文档,根据接口文档&…...
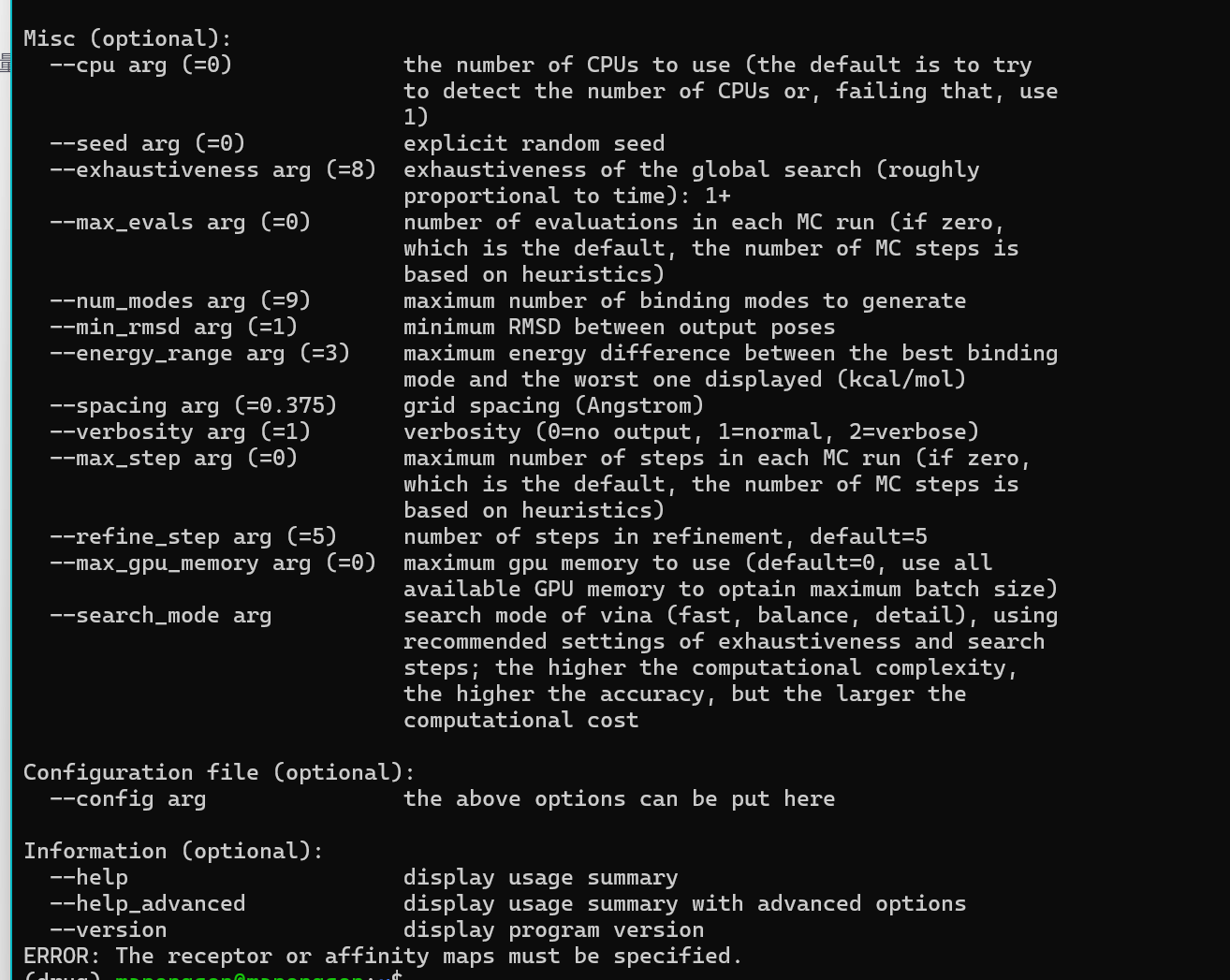
Uni-Dock:GPU 分子对接使用教程
github文件下载: git clone https://github.com/dptech-corp/Uni-Dock.git cd Uni-Dock/example/screening_test wget https://github.com/dptech-corp/Uni-Dock/releases/download/1.0.0/unidock 将此文件加入到全局变量中 chmod x unidock sudo mv unidock /…...
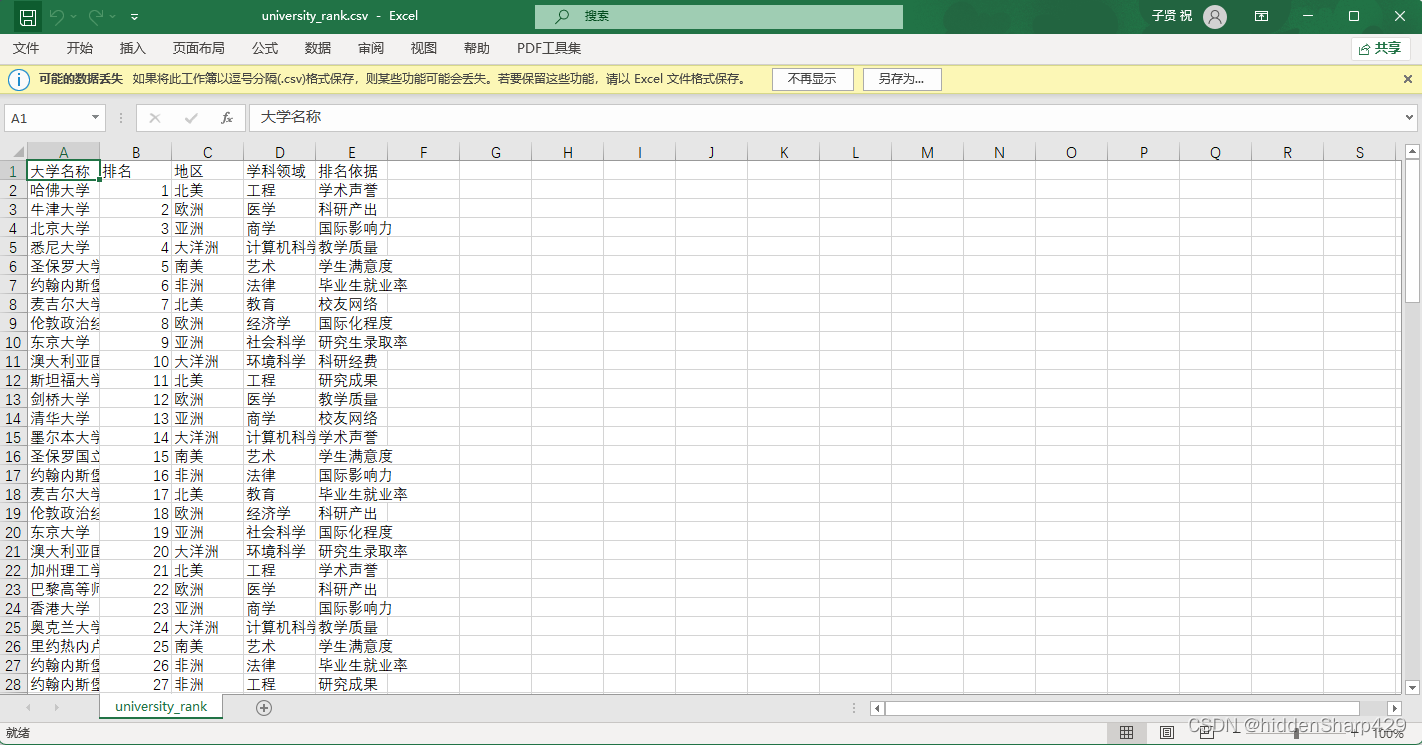
【Python】数据分析+数据挖掘——掌握Python和Pandas中的单元格替换操作
1. 前言 数据处理和清洗是数据分析和机器学习中至关重要的步骤。在数据处理过程中,我们经常需要对数据集进行清洗和转换,其中单元格替换是一个常用的技术。Python作为一种功能强大且灵活的编程语言,为数据处理提供了丰富的工具和库。Pandas库…...

Godot 4 源码分析 - 增加格式化字符串功能
Godot 4的主要字符串类型为String,已经设计得比较完善了,但有一个问题,格式化这块没怎么考虑。 String中有一个format函数,但这个函数只有两个参数,这咋用? String String::format(const Variant &va…...
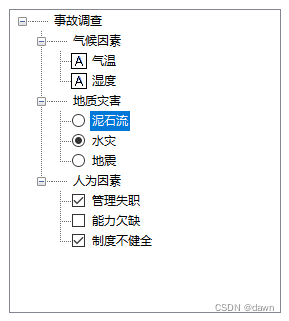
C#中XML文档与Treeview控件操作的数据同步
在前文《C#使用XML和Treeview结合实现复杂数据采集功能》中,使用Treeview展示了XML的数据,问题是如果在Treeview上进行了操作,怎样同步更改XML数据的内容呢? 这个问题看似简单,实现起来有一点小麻烦。 要实现的操作功能…...
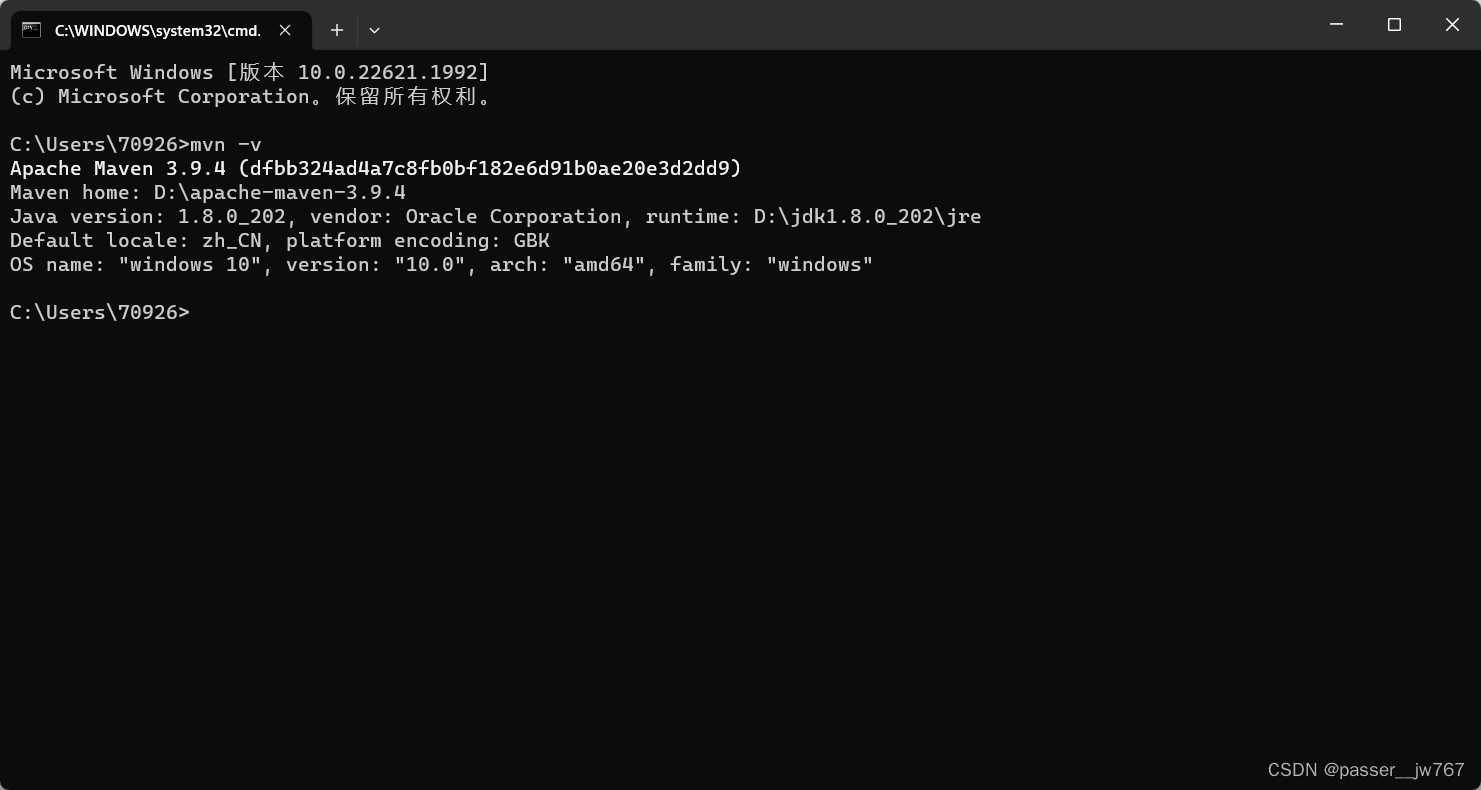
【Java Web基础】mvn命令、Maven的安装与配置
本文极大程度上来自Maven安装(超详解),但是担心安的过程中遇到什么不一样的问题,顺便加深印象,所以还是打算自己弄一篇。 目录 第一步:Download Maven第二步:解压与安装2.1 解压2.2 安装 第一步:Download …...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...
