matlab离散系统仿真分析——电机
目录
1.电机模型
2.数字PID控制
3.MATLAB数字仿真分析
3.1matlab程序
3.2 仿真结果
4. SIMULINK仿真分析
4.1simulink模型
4.2仿真结果
1.电机模型
即:
其中:J = 0.0067;B = 0.10
2.数字PID控制
首先我们来看一下连续PID:
![]()

简单说来,PID控制器各校正环节的作用如下:
(1)比例环节:成比例地反映控制系统的偏差信号error(t),偏差一旦产生,控制器立即产生控制作用,以减少偏差。
(2)积分环节:主要用于消除静差,提高系统的无差度。积分作用的强弱取决于积分时间常数T,T越大,积分作用越弱,反之则越强。
(3)微分环节:反映偏差信号的变化趋势(变化速率),并能在偏差信号变得太大之前,在系统中引入一个有效的早期修正信号,从而加快系统的动作速度,减少调节时间。
按模拟PID控制算法,以一系列的采样时刻点kT代表连续时间t,以矩形法数值积分近似代替积分,以一阶后向差分近似代替微分,即:

3.MATLAB数字仿真分析
3.1matlab程序
主程序:
clear all
clc;
xk = zeros(2,1);%定义初始状态
ts = 0.001;
e_1 = 0;
u_1 = 0;
for k = 1:2000 %仿真时间=k*tstime(k)= k*ts;xd(k) = 0.5*sin(2*pi*k*ts);%跟踪位移信号,即x1跟踪xdtspan = [(k-1)*ts k*ts];%当前时刻求解的积分区间para = u_1;%控制输入[tt,x] = ode45('Plant',tspan,xk,[],para);xk = x(length(x),:);%取求解向量的最后一行,且作为下一时刻的初始状态x1(k) = xk(1);%选位移信息作为输出向量e(k) = xd(k)-x1(k);%误差比例 de(k) = (e(k)-e_1)/ts;%误差微分P = 20;D = 0.5;u(k) = P*e(k)+D*de(k);u_1 = u(k);%更新当前时刻的控制输入e_1 = e(k);%更新当前时刻的跟踪误差
end
figure(1)
plot(time,x1,'k',time,xd,'r','linewidth',1)
legend('x1','xd')
xlabel('t');ylabel('x1(转速)')
figure(2)
plot(time,u,'k','linewidth',1)
xlabel('t');ylabel('PD控制输入')
figure(3)
plot(time,e,'k','linewidth',1)
xlabel('t');ylabel('跟踪误差e')
figure(4)
plot(time,de,'k','linewidth',1)
xlabel('t');ylabel('跟踪误差变化率de')
% function dx = Plant(tspan,x,flag,para)
% u = para;
% J = 0.0067;B = 0.1;
% dx = zeros(2,1);%注意要将状态变量定位列向量,否则系统默认为行向量
% dx(1) = x(2);
% dx(2) = -(B/J)*x(2)+u/J;
% end电机模型:
function dx = Plant(tspan,x,flag,para)
% tspan:积分时间段、x当前求解微分方程时刻的初始状态、para:当前时刻的控制输入
u = para;
J = 0.0067;B = 0.1;
dx = zeros(2,1);%注意要将状态变量定位列向量,否则系统默认为行向量
dx(1) = x(2);
dx(2) = -(B/J)*x(2)+u/J;
end3.2 仿真结果




4. SIMULINK仿真分析
对比一下纯数字仿真和simulink建模仿真效果:
4.1simulink模型
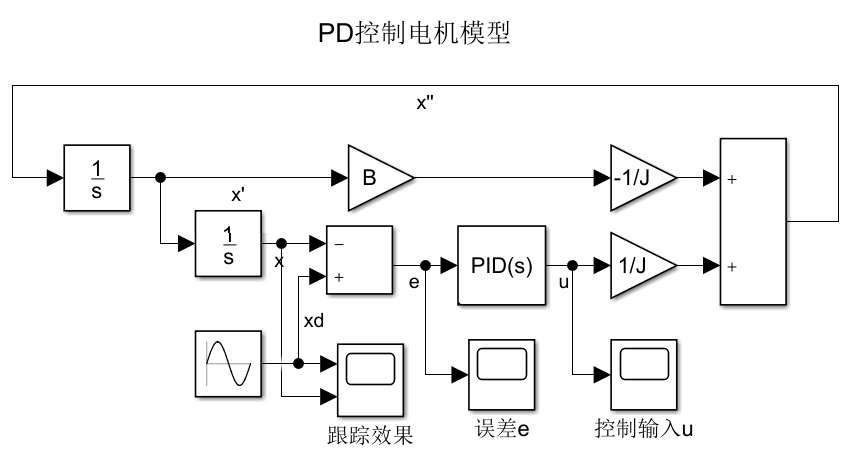
4.2仿真结果
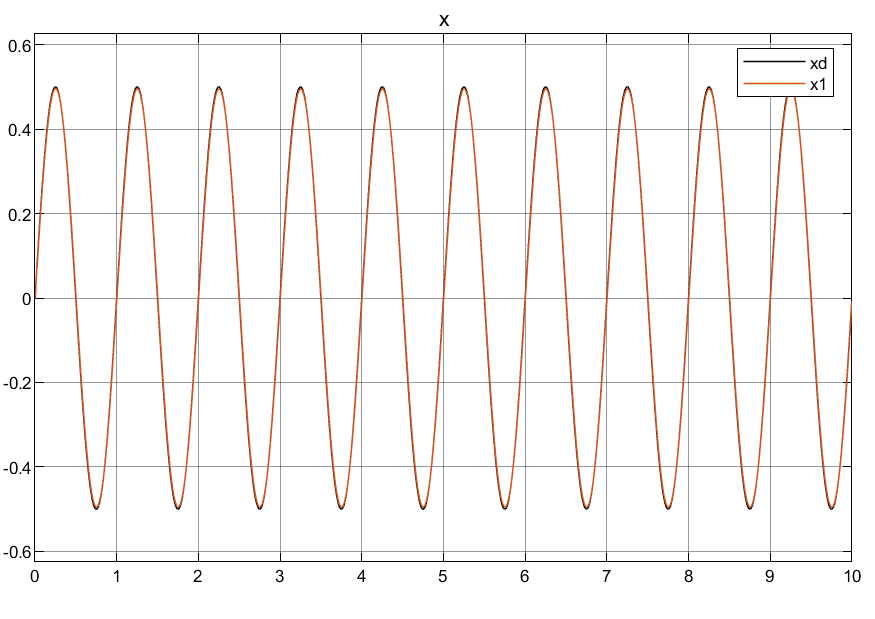

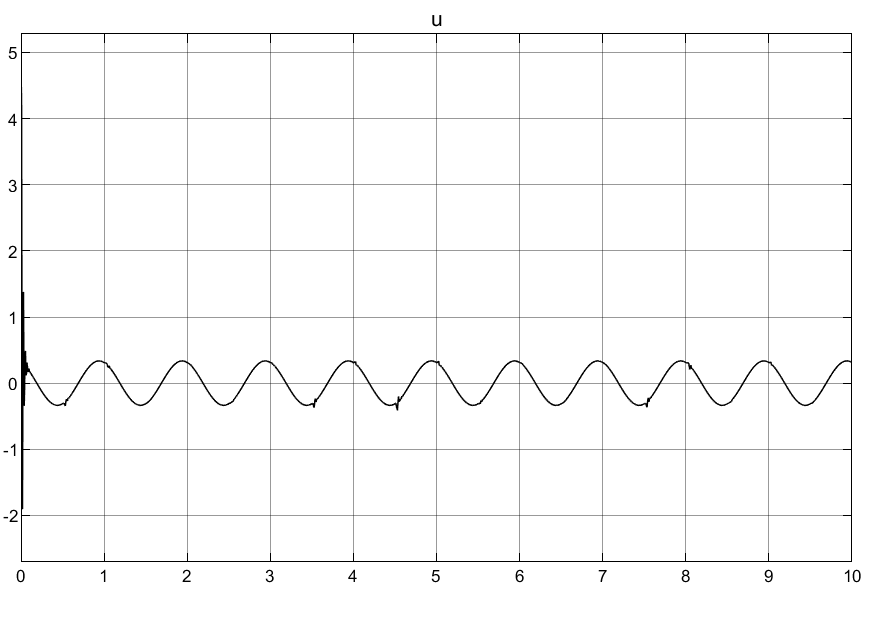
相关文章:

matlab离散系统仿真分析——电机
目录 1.电机模型 2.数字PID控制 3.MATLAB数字仿真分析 3.1matlab程序 3.2 仿真结果 4. SIMULINK仿真分析 4.1simulink模型 4.2仿真结果 1.电机模型 即: 其中:J 0.0067;B 0.10 2.数字PID控制 首先我们来看一下连续PID࿱…...
一文学会进程控制
目录进程的诞生fork函数fork的本质fork的常规用法fork调用失败的原因进程的死亡进程退出的场景常见的进程退出方法正常终止(代码跑完)echo $?main函数返回调用exit调用_exitexit和_exit的区别进程等待进程等待的重要性进程等待的函数waitwaitpid进程退出…...

5.2 BGP水平分割
5.2.2实验2:BGP水平分割 1. 实验目的 熟悉BGP水平分割的应用场景掌握BGP水平分割的配置方法 2. 实验拓扑 实验拓扑如图5-2所示: 图5-2:BGP水平分割 3. 实验步骤 (1)配置IP地址 R1的配置 <Huawei>…...

华为OD机试 - TLV 编码 | 备考思路,刷题要点,答疑 【新解法】
最近更新的博客 【新解法】华为OD机试 - 关联子串 | 备考思路,刷题要点,答疑,od Base 提供【新解法】华为OD机试 - 停车场最大距离 | 备考思路,刷题要点,答疑,od Base 提供【新解法】华为OD机试 - 任务调度 | 备考思路,刷题要点,答疑,od Base 提供【新解法】华为OD机试…...
【C语言每日一题】——猜名次
【C语言每日一题】——猜名次😎前言🙌猜名次🙌解题思路分享:😍解题源码分享:😍总结撒花💞😎博客昵称:博客小梦 😊最喜欢的座右铭:全神…...

Agilent E4982A、Keysight E4982A、LCR 表,1 MHz 至 3 GHz
Agilent E4982A、Keysight E4982A、HP E4982A LCR 表,1 MHz 至 3 GHz 产品概览 KEYSIGHT E4982A(安捷伦) Keysight E4982A LCR 表为需要高频(1 MHz 至 3 GHz)阻抗测试的无源元件制造行业提供一流的性能,…...

SAP 系统的配置传输
在SAP项目的实施过程中,经常会遇到关于配置传输的问题。即我们在某个client下面做系统配置,配好了之后再传到其他系统之中。 配置传输分为两种情况:同服务器配置传输,异服务器配置传输。同服务器配置传输: 在DEV配置cl…...
)
华为OD机试 - 喊七(Python)
喊七 题目 喊 7,是一个传统的聚会游戏, N 个人围成一圈,按顺时针从1 - 7编号, 编号为1的人从1开始喊数, 下一个人喊得数字是上一个人喊得数字+1, 但是当将要喊出数字7的倍数或者含有7的话, 不能喊出,而是要喊过。 假定N个人都没有失误。 当喊道数字k时, 可以统计每…...
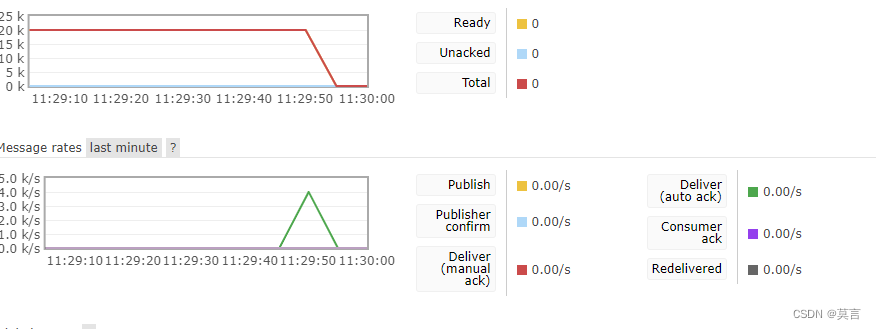
Docker下快速搭建RabbitMQ单例及集群
引子生命在于折腾,为上数据实时化用到了消息传送的内容,当时也和总公司人员商量选型,kafka不能区分分公司就暂定用了RbtMQ刚好个人也在研究容器及分布式部署相关内容就在docker上实践单机 docker(要想快 先看问题 避免踩坑&#x…...

python代码写开心消消乐
♥️作者:小刘在C站 ♥️个人主页:小刘主页 ♥️每天分享云计算网络运维课堂笔记,努力不一定有收获,但一定会有收获加油!一起努力,共赴美好人生! ♥️夕阳下,是最美的绽放,树高千尺,落叶归根人生不易,人间真情 目录 一.python是什么 二.游戏代码效果呈现 三.主代...
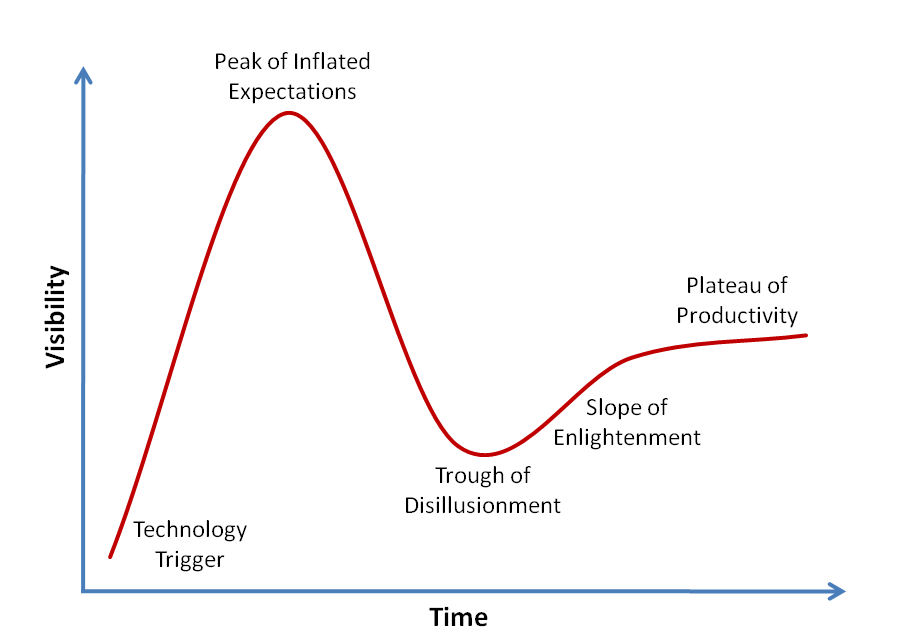
【郭东白架构课 模块一:生存法则】09|法则四:为什么要顺应技术的生命周期?
你好,我是郭东白。今天我们来讲架构师的第四条生存法则,那就是尊重技术的生命周期。 人类的各种活动都要遵循事物的客观生命周期。不论是农业社会种田打渔,还是资本社会投资创业,行动太早或太晚,都会颗粒无收。技术也…...
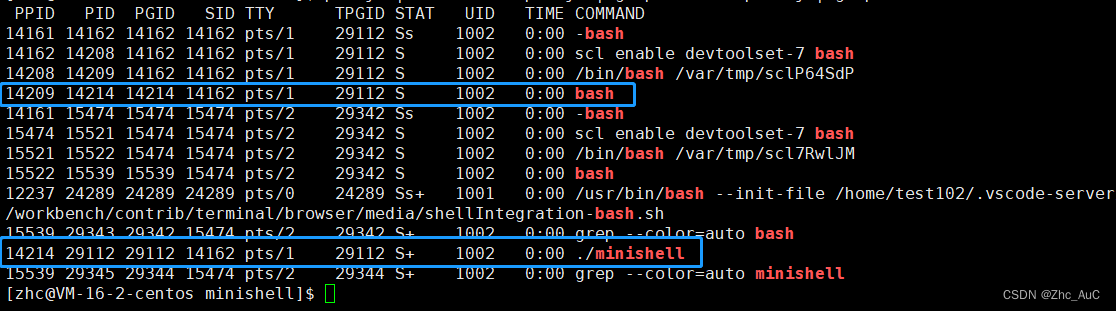
Linux之进程控制
一.进程创建 1.1 fork函数 我们创建进程的方式有./xxx和fork()两种 在linux中fork函数时非常重要的函数,它从已存在进程中创建一个新进程。新进程为子进程,而原进程为父进程。 #include <unistd.h> pid_t fork(void); 返回值:自进程…...

SpringBoot社区版专业版带你配置热部署
💟💟前言 友友们大家好,我是你们的小王同学😗😗 今天给大家打来的是 SpringBoot社区版专业版带你配置热部署 希望能给大家带来有用的知识 觉得小王写的不错的话麻烦动动小手 点赞👍 收藏⭐ 评论…...

影响AFE采样精度的因素有哪些?
**AFE(Analog Front End)**是模拟前端电路的缩写,它是模拟信号传感器和数字信号处理器之间的连接点。AFE采样精度是指模拟信号被数字化后的准确度,对于很多电子设备来说,这是一个至关重要的性能指标。本文将介绍影响AF…...

mysqlbackup备份报error:redo log was overwritten
问题原因 备份时redo log被覆盖 解决方案 方法1:增加innodb_log_file_size、innodb_log_files_in_group大小,需要重启数据库 vi my.cnf innodb_log_file_size 2G innodb_log_files_in_group 4 方法2: 动态配置redo log archive,不需要重启…...

Android支持库
# 支持库 注意:Android 9.0(API 级别 28)发布后,新版支持库 AndroidX 也随之诞生,它属于 Jetpack。除了现有的支持库,AndroidX 库还包含最新的 Jetpack 组件。 您可以继续使用此支持库以往的工件(这里指的是版本 27 及更早版本,且已打包为 android.support.*)在 Googl…...
Vue:filters过滤器
日期、时间格式化是Vue前端项目中较为常遇到的一个需求点,此处,围绕Vue的过滤器来介绍如何更为优雅的解决此类需求。 过滤器filters使用注意点 Vue允许开发者自定义过滤器,可以实现一些常见的文本格式化等需求。 使用时要注意的点在于&#…...
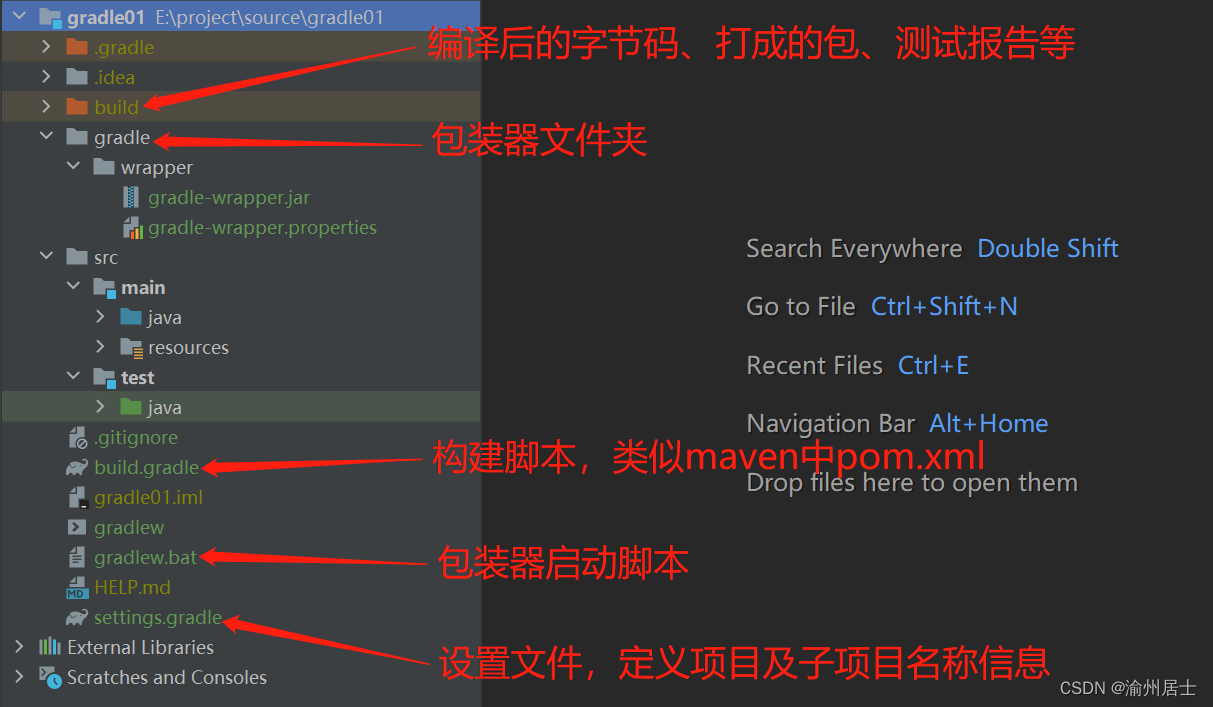
Windows环境下安装和配置Gradle
1. 概述 Gradle是Google公司基于JVM开发的一款项目构建工具,支持Maven,JCenter多种第三方仓库,支持传递性依赖管理,使用更加简洁和支持多种语言的build脚步文件,更多详情可以参阅Gradle官网 2. 下载 由于Gradle与S…...

数据结构时间空间复杂度笔记
🕺作者: 迷茫的启明星 本篇内容:数据结构时间空间复杂度笔记 😘欢迎关注:👍点赞🙌收藏✍️留言 🏇家人们,码字不易,你的👍点赞🙌收藏❤…...
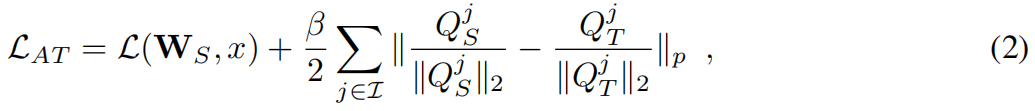
基于注意力的知识蒸馏Attention Transfer原理与代码解析
paper:Paying More Attention to Attention: Improving the Performance of Convolutional Neural Networks via Attention Transfercode:https://github.com/megvii-research/mdistiller/blob/master/mdistiller/distillers/AT.py背景一个流行的假设是存…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...

CppCon 2015 学习:Time Programming Fundamentals
Civil Time 公历时间 特点: 共 6 个字段: Year(年)Month(月)Day(日)Hour(小时)Minute(分钟)Second(秒) 表示…...
