第三章 图论 No.3 flody之多源汇最短路,传递闭包,最小环与倍增
文章目录
- 多源汇最短路:1125. 牛的旅行
- 传递闭包:343. 排序
- 最小环:344. 观光之旅
- 345. 牛站
flody的四个应用:
- 多源汇最短路
- 传递闭包
- 找最小环
- 恰好经过k条边的最短路 倍增
多源汇最短路:1125. 牛的旅行
1125. 牛的旅行 - AcWing题库

直径概念:同一连通块中,两个距离最远的点之间的距离
如何求直径?由于图中存在着两个连通块,所以直接对全图做一个flody,就能更新出任意两点间的距离,距离大于正无穷的一半时,说明两点处于不同连通块中
题目要连接两个连通块,并计算所有连接方法下,原连通块与新连通块中,最大直径的最小值
可以枚举所有的连接方式,维护出新连通块的直径最小值,将其与原连通块的两个直径比较,取三者的最小值即可
假设连接了属于不同连通块的i和j,那么经过这条边的直径等于get_dis(i, j) + dmax(i) + dmax(j),其中get_dis表示两点间的距离,dmax(i)表示在原连通块中,i与距离i最远的点的距离
那么新连通块的直径是原连通块的直径与经过连接两连通块的边的直径中的最大值
最终要在原连通块的直径与新连通块的直径最大值中取min
在计算新连通块的直径最大值时,需要在原连通块与当前新连通块的直径中取max,由于每中不同连接方式都要与原连通块的直径取max,我们可以放到最后在与之取max
先计算经过连接两连通块的边的直径的最大值,在与原连通块的直接取max
#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>#define x first
#define y secondusing namespace std;typedef pair<double, double> PDD;const int N = 155;
const double INF = 1e20;int n;
PDD q[N];
double d[N][N];
double maxd[N];
char g[N][N];double get_dist(PDD a, PDD b)
{double dx = a.x - b.x;double dy = a.y - b.y;return sqrt(dx * dx + dy * dy);
}int main()
{cin >> n;for (int i = 0; i < n; i ++ ) cin >> q[i].x >> q[i].y;for (int i = 0; i < n; i ++ ) cin >> g[i];for (int i = 0; i < n; i ++ )for (int j = 0; j < n; j ++ )if (i == j) d[i][j] = 0;else if (g[i][j] == '1') d[i][j] = get_dist(q[i], q[j]);else d[i][j] = INF;for (int k = 0; k < n; k ++ )for (int i = 0; i < n; i ++ )for (int j = 0; j < n; j ++ )d[i][j] = min(d[i][j], d[i][k] + d[k][j]);double r1 = 0;for (int i = 0; i < n; i ++ ){for (int j = 0; j < n; j ++ )if (d[i][j] < INF / 2)maxd[i] = max(maxd[i], d[i][j]);r1 = max(r1, maxd[i]);}double r2 = INF;for (int i = 0; i < n; i ++ )for (int j = 0; j < n; j ++ )if (d[i][j] > INF / 2)r2 = min(r2, maxd[i] + maxd[j] + get_dist(q[i], q[j]));
cout << r1 << ' ' << r2 << endl;printf("%.6lf\n", max(r1, r2));return 0;
}
传递闭包:343. 排序
343. 排序 - AcWing题库

将简洁相连的点连接起来,成为传递闭包
用flody可以在 O ( n 3 ) O(n^3) O(n3)的时间复杂度内计算出传递闭包
用邻接矩阵g存储图,传递闭包保存在矩阵d上
g[i][j]为1,表示存在一条从i到j的边,g[i][j]为0表示不存在
初始化:d[i][j] = g[i][j]
flody的更新换为:
d[i][j] |= d[i][k] && d[k][j]
题目中的小于关系就是一条边,每次读取一个小于关系,就在图中添加一条边,然后求传递闭包
三种情况:
- 矛盾:此时
d[i][[i] = 1,表示i存在自环。因为d[i][j] == 1 && d[j][i] == 1,求完传递闭包后d[i][i] = 1 - 情况未确定,
d[i][j]和d[j][i]都为0,表示i和j之间没有边,即没有小于关系 - 情况确定,遍历完d数组,无以上情况,此时情况确定
当情况确定时,如何按小于关系输出变量? O ( n 2 ) O(n^2) O(n2)地暴力搜索所有点,将已经输出的变量进行标记,若当前点是某一条边的终点并且起点未被标记,说明存在小于当前变量的变量,且未被输出
若当前变量不是任意一条边的终点或者起点已经被标记,那么输出该变量并标记
#include <cstring>
#include <iostream>
#include <algorithm>using namespace std;const int N = 26;int n, m;
bool g[N][N], d[N][N];
bool st[N];void floyd()
{memcpy(d, g, sizeof d);for (int k = 0; k < n; k ++ )for (int i = 0; i < n; i ++ )for (int j = 0; j < n; j ++ )d[i][j] |= d[i][k] && d[k][j];
}int check()
{for (int i = 0; i < n; i ++ )if (d[i][i])return 2;for (int i = 0; i < n; i ++ )for (int j = 0; j < i; j ++ )if (!d[i][j] && !d[j][i])return 0;return 1;
}char get_min()
{for (int i = 0; i < n; i ++ )if (!st[i]){bool flag = true;for (int j = 0; j < n; j ++ )if (!st[j] && d[j][i]){flag = false;break;}if (flag){st[i] = true;return 'A' + i;}}
}int main()
{while (cin >> n >> m, n || m){memset(g, 0, sizeof g);int type = 0, t;for (int i = 1; i <= m; i ++ ){char str[5];cin >> str;int a = str[0] - 'A', b = str[2] - 'A';if (!type){g[a][b] = 1;floyd();type = check();if (type) t = i;}}if (!type) puts("Sorted sequence cannot be determined.");else if (type == 2) printf("Inconsistency found after %d relations.\n", t);else{memset(st, 0, sizeof st);printf("Sorted sequence determined after %d relations: ", t);for (int i = 0; i < n; i ++ ) printf("%c", get_min());printf(".\n");}}return 0;
}
最小环:344. 观光之旅
344. 观光之旅 - AcWing题库
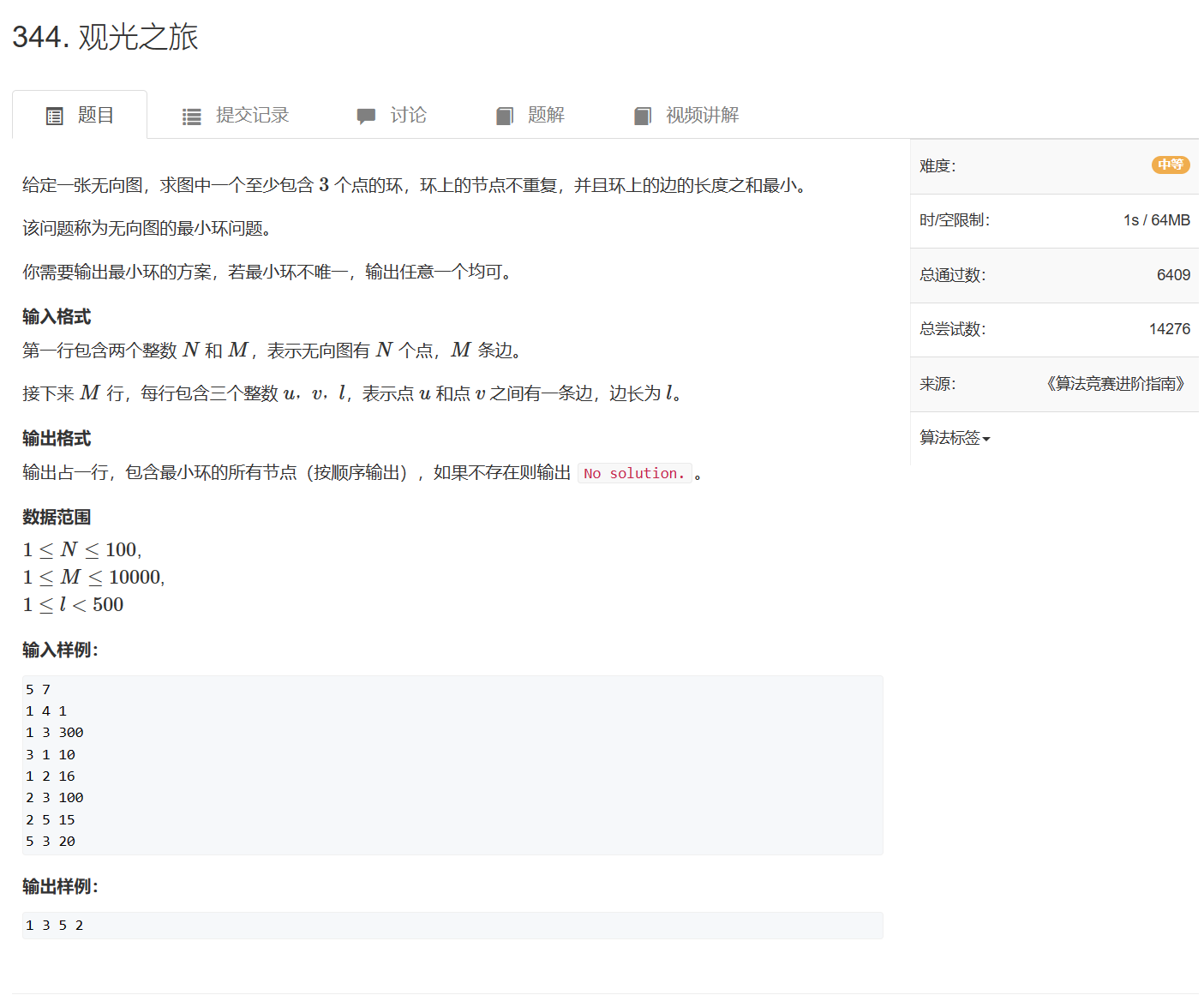
如何求第k类的最小环?
思考flody的三重循环,在第一重k循环时,我们已经知道从i到j只经过1~k-1这些点的最短路径
若i,j,k三者能构成环,那么i和k直接相连,i和j也直接相连
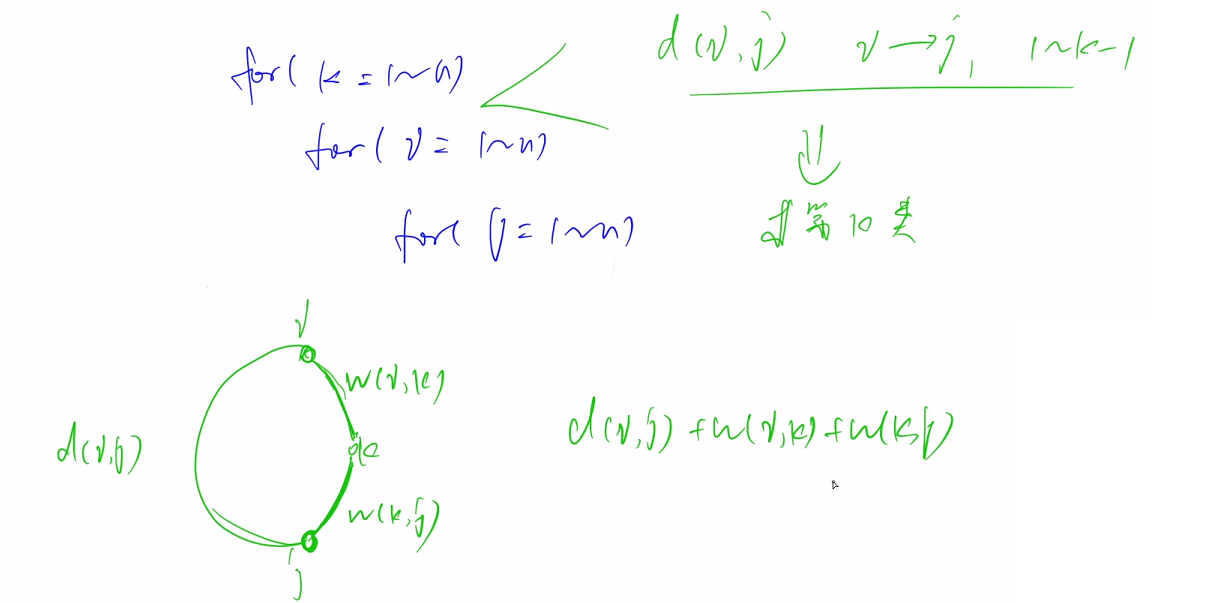
此时i,j,k构成的最小环的长度就等于d[i][j] + g[i][k] + g[k][j]
d[i][j]为i到j的最短距离
所以在循环k时,就可以枚举所有的i和j,得到包含i,j,k三点的最小环,在这些最小环中取min即可
此外,还需要求具体方案
只需要在更新的时候:d[i][j] > d[i][k] + d[k][j]时,记录i到j的最短路经过了k即可,即pos[i][j] = k
求i到j的最短路时,采用递归的方式,get_path(i, j),该函数将顺序输出i到j的最短路中,除了i和j的所有中间点
get_path(i, j),通过pos[i][j]的值,将i到j划分称i到k到j,递归get_path(i, k)与get_path(k, j),直到pos[i][j]为0,说明i到j之间无之间点,即两点之间相连
#include <iostream>
#include <cstring>
using namespace std;typedef long long LL;
const int N = 110, M = 20010, INF = 0x3f3f3f3f;
int g[N][N], d[N][N];
int path[N], cnt;
int pos[N][N];
int n, m;void get_path(int i, int j)
{if (pos[i][j] == 0) return;int k = pos[i][j];get_path(i, k);path[cnt ++ ] = k;get_path(k, j);
}int main()
{scanf("%d%d", &n, &m);memset(g, 0x3f, sizeof(g));for (int i = 1; i <= n; ++ i ) g[i][i] = 0;for (int i = 1; i <= m; ++ i ){int x, y, d;scanf("%d%d%d", &x, &y, &d);g[x][y] = g[y][x] = min(g[x][y], d);}memcpy(d, g, sizeof(g));int res = INF;for (int k = 1; k <= n; ++ k ){for (int i = 1; i < k; ++ i )for (int j = i + 1; j < k; ++ j ){if (res > (LL)d[i][j] + g[i][k] + g[k][j]){res = d[i][j] + g[i][k] + g[k][j];cnt = 0;path[cnt ++ ] = k; // 从k开始记录环path[cnt ++ ] = i;get_path(i, j);path[cnt ++ ] = j;}}for (int i = 1; i <= n; ++ i )for (int j = 1; j <= n; ++ j)if (d[i][j] > d[i][k] + d[k][j]){d[i][j] = d[i][k] + d[k][j];pos[i][j] = k;}}if (res == INF) puts("No solution.");else for (int i = 0; i < cnt; ++ i ) printf("%d ", path[i]);return 0;
}
一些需要注意的地方:res > (LL)d[i][j] + g[i][k] + g[k][j]
不开LL的话,可能三个INF相加会导致爆int
枚举最小环时,j从i+1开始,保证j比i的同时,也保证最小环中至少有三个点
没看懂,先跳过
345. 牛站
345. 牛站 - AcWing题库
flody的变形,表示的状态发生变化, f ( k , i , j ) f(k, i, j) f(k,i,j)表示从i到j,恰好经过k条边的最短路
d [ a + b , i , j ] = d [ a , i , k ] + d [ b , k , j ] d[a+b, i, j] = d[a, i, k] + d[b, k, j] d[a+b,i,j]=d[a,i,k]+d[b,k,j]
从i到j恰好经过a+b条边的最短路径,假设中间点为k,将路径划分称两段,经过a条边从i到k,经过b条边从k到j。两段分别取最短路径,相加得到我们需要的最短路径
枚举所有的k,取min后就能得到 d [ a + b , i , j ] d[a+b, i, j] d[a+b,i,j]
枚举所有的k后,枚举不同的i和j,转换成代码就是flody的形式
相关文章:

第三章 图论 No.3 flody之多源汇最短路,传递闭包,最小环与倍增
文章目录 多源汇最短路:1125. 牛的旅行传递闭包:343. 排序最小环:344. 观光之旅345. 牛站 flody的四个应用: 多源汇最短路传递闭包找最小环恰好经过k条边的最短路 倍增 多源汇最短路:1125. 牛的旅行 1125. 牛的旅行 …...
Leetcode-每日一题【剑指 Offer 17. 打印从1到最大的n位数】
题目 输入数字 n,按顺序打印出从 1 到最大的 n 位十进制数。比如输入 3,则打印出 1、2、3 一直到最大的 3 位数 999。 示例 1: 输入: n 1输出: [1,2,3,4,5,6,7,8,9] 说明: 用返回一个整数列表来代替打印 n 为正整数 解题思路 前置知识 M…...
远程调试MySQL内核
1 vscode 需要安装remote-ssh插件 安装成功后,登录: 默认远程服务器的登录 ssh rootip注意,Linux需要设置root远程登录; 2 安装debug扩展 C\C extemsion Pack C\C3 设置Attach进程 {// Use IntelliSense to learn about poss…...
前端学习---vue2--选项/数据--data-computed-watch-methods-props
写在前面: vue提供了很多数据相关的。 文章目录 data 动态绑定介绍使用使用数据 computed 计算属性介绍基础使用计算属性缓存 vs 方法完整使用 watch 监听属性介绍使用 methodspropspropsData data 动态绑定 介绍 简单的说就是进行双向绑定的区域。 vue实例的数…...
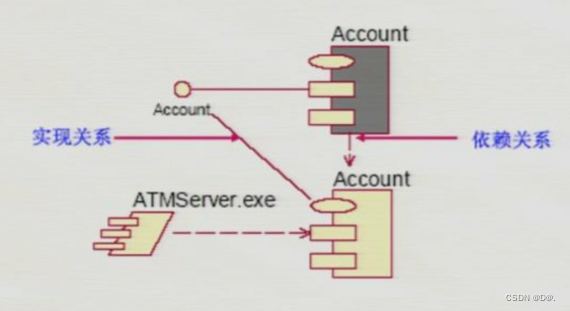
UML-构件图
目录 1.概述 2.构件的类型 3.构件和类 4.构件图 1.概述 构件图主要用于描述各种软件之间的依赖关系,例如,可执行文件和源文件之间的依赖关系,所设计的系统中的构件的表示法及这些构件之间的关系构成了构件图 构件图从软件架构的角度来描述…...

uniapp使用视频地址获取视频封面
很多时候我们都需要使用视频的第一帧当作视频的封面,今天我们从uni-app的安卓app这个环境来实现下这个需求。文中需要你对uniapp的renderjs有一定了解,可以先看我的这篇文章初识renderjs uniapp 安卓APP端(ios未测试) 方法&…...

java操作PDF:转换、合成、切分
将PDF每一页切割成图片 PDFUtils.cutPNG("D:/tmp/1.pdf","D:/tmp/输出图片路径/"); 将PDF转换成一张长图片 PDFUtils.transition_ONE_PNG("D:/tmp/1.pdf"); 将多张图片合并成一个PDF文件 PDFUtils.merge_PNG("D:/tmp/测试图片/"); 将多…...
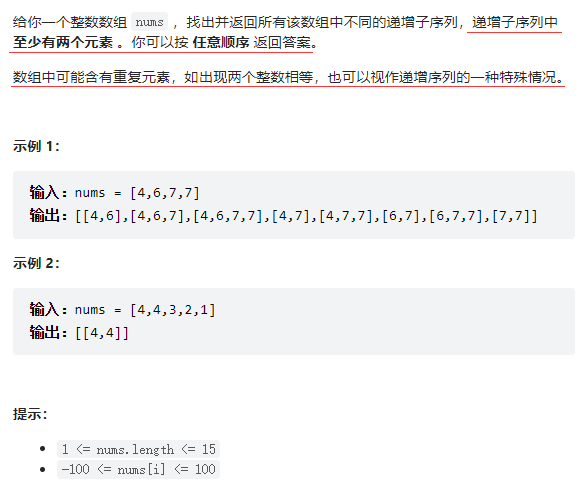
递增子序列——力扣491
文章目录 题目描述递归枚举 + 减枝题目描述 递归枚举 + 减枝 递归枚举子序列的通用模板 vector<vector<int>> ans; vector<int> temp; void dfs(int cur...

解密!品牌独立站为何能成为外国消费者的心头爱?
中国人做事强调要知其然、知其所以然、知其所以必然。这一理念非常符合新时代中国跨境出海品牌独立站的发展思路。在做好品牌独立站之前,我们也必须知其然(什么是独立站?),知其所以然(为什么要建独立站&…...
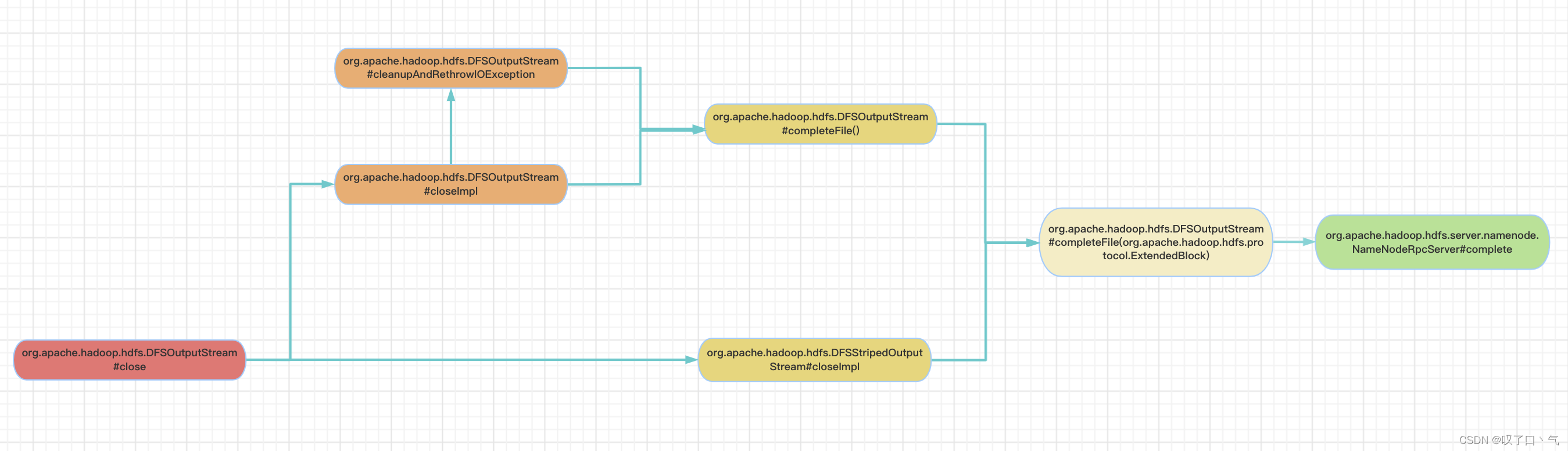
【HDFS】每天一个RPC系列----complete(二):客户端侧
上图给出了最终会调用到complete RPC的客户端侧方法链路(除去Router那条线了)。 org.apache.hadoop.hdfs.DFSOutputStream#completeFile(org.apache.hadoop.hdfs.protocol.ExtendedBlock): 下面这个方法在complete rpc返回true之前,会进行重试,直到超过最大重试次数抛异…...
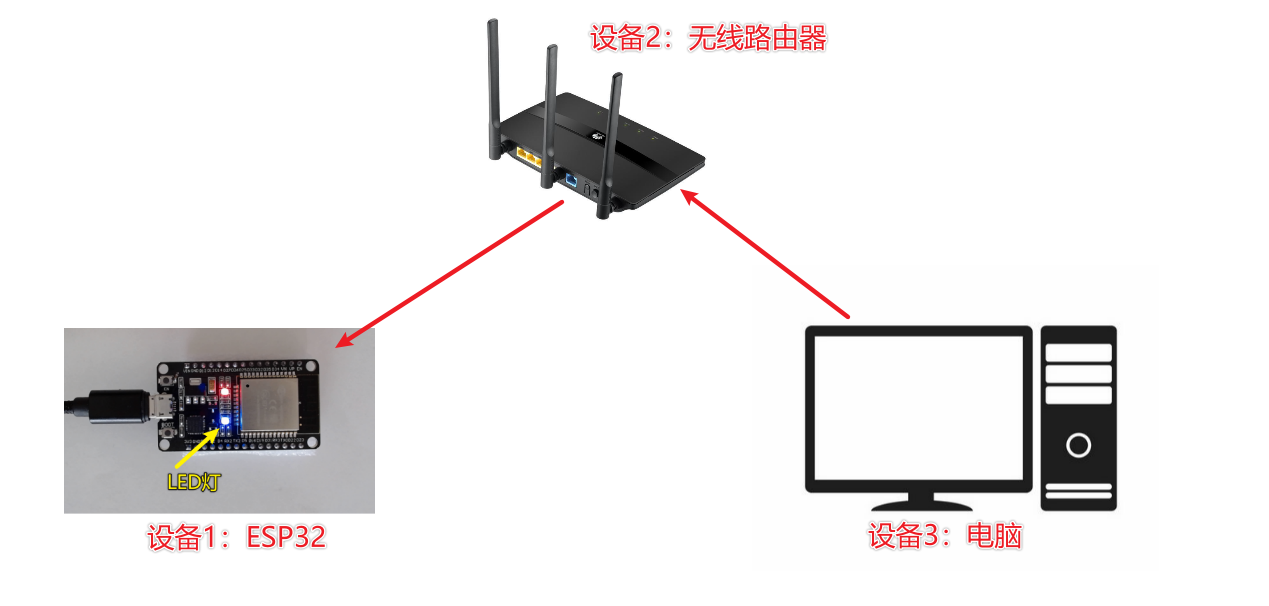
五、PC远程控制ESP32 LED灯
1. 整体思路 2. 代码 # 整体流程 # 1. 链接wifi # 2. 启动网络功能(UDP) # 3. 接收网络数据 # 4. 处理接收的数据import socket import time import network import machinedef do_connect():wlan = network.WLAN(network.STA_IF)wlan.active(True)if not wlan.isconnected(…...

详解PHP反射API
PHP中的反射API就像Java中的java.lang.reflect包一样。它由一系列可以分析属性、方法和类的内置类组成。它在某些方面和对象函数相似,比如get_class_vars(),但是更加灵活,而且可以提供更多信息。反射API也可与PHP最新的面向对象特性一起工作&…...

打开虚拟机进行ip addr无网络连接
打开虚拟机进行ip addr无网络连接 参考地址:https://www.cnblogs.com/Courage129/p/16796390.html 打开虚拟机进行ip addr无网络连接。 输入下面的命令, sudo dhclient ens33 会重新分配一个新的ip地址,但是此时的ip地址已经不是我原先在虚…...
Spring Boot如何整合mybatisplus
文章目录 1. 相关配置和代码2. 整合原理2.1 spring boot自动配置2.2 MybatisPlusAutoConfiguration2.3 debug流程2.3.1 MapperScannerRegistrar2.3.2MapperScannerConfigurer2.3.3 创建MybatisPlusAutoConfiguration2.3.4 创建sqlSessionFactory2.3.5 创建SqlSessionTemplate2.…...
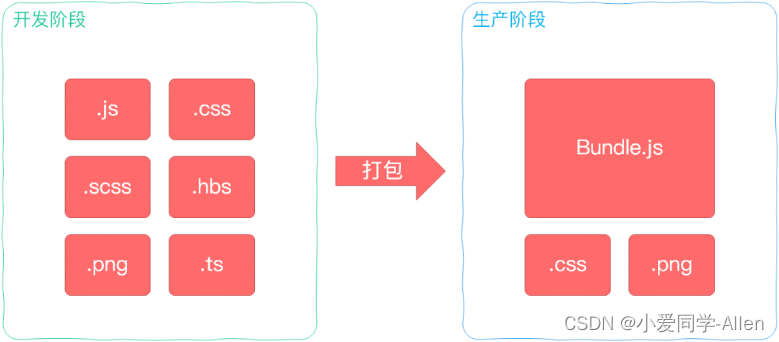
webpack基础知识一:说说你对webpack的理解?解决了什么问题?
一、背景 Webpack 最初的目标是实现前端项目的模块化,旨在更高效地管理和维护项目中的每一个资源 模块化 最早的时候,我们会通过文件划分的形式实现模块化,也就是将每个功能及其相关状态数据各自单独放到不同的JS 文件中 约定每个文件是一…...
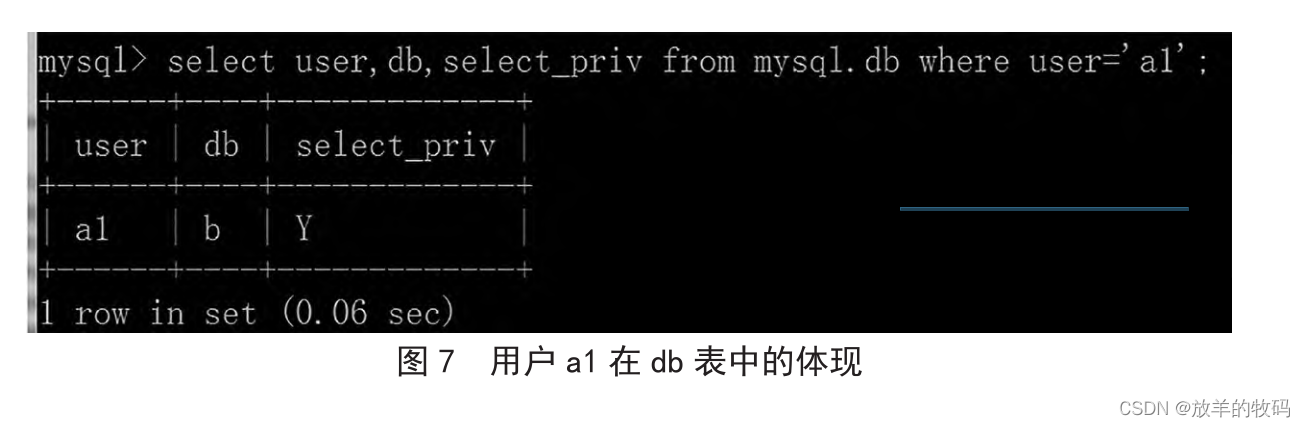
小研究 - 基于 MySQL 数据库的数据安全应用设计(二)
信息系统工程领域对数据安全的要求比较高,MySQL 数据库管理系统普遍应用于各种信息系统应用软件的开发之中,而角色与权限设计不仅关乎数据库中数据保密性的性能高低,也关系到用户使用数据库的最低要求。在对数据库的安全性进行设计时…...

大数据-数据内容分类
大数据-数据内容分类 结构化数据 可以使用关系型数据库表示和存储,可以用二维表来逻辑表达实现的数据 结构化数据:二维表(关系型) 结构化数据:先有结构、再有数据 数据以行为单位,一行数据表示一个实体…...

Babel编译与Webpack
目录 Babel初识BabelBabel 使用方式使用 Babel 前的准备工作 WebpackWebpack介绍Webpack初体验Webpack核心概念入口(entry)出口(output)加载 (loader)插件(plugins) Babel Babel官网: https://babeljs.io/…...

0805hw
1. #include <myhead.h> void Bub_sort(int *arr,int n)//冒泡排序 {for(int i1;i<n;i){int count0;for(int j0;j<n-i;j){if(arr[j]>arr[j1]){int temparr[j];arr[j]arr[j1];arr[j1]temp;count;}}if(count0){break;}}printf("冒泡排序后输出结果:\n"…...

ROS实现机器人移动
开源项目 使用是github上六合机器人工坊的项目。 https://github.com/6-robot/wpr_simulation.git 机器人运动模型 运动模型如下所示:👇 机器人运动的消息包: 实现思路:👇 为什么要使用/cmd_vel话题。因为这…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...
