题解 | #C.idol!!# 2023牛客暑期多校6
C.idol!!
数学
题目大意
正整数 n n n 的双阶乘 n ! ! n!! n!! 表示不超过 n n n 且与 n n n 有相同奇偶性的所有正整数乘积
求对于给定 n n n , ∏ i = 1 n i ! ! \prod\limits_{i=1}^n i!! i=1∏ni!! 的后缀 0 0 0 个数
解题思路
根据双阶乘的性质,可以得到: ( n − 1 ) ! ! × n ! ! = n ! (n-1)!!\times n!!=n! (n−1)!!×n!!=n!
因此对于给定的 n n n ,原式可化为:
∏ i = 1 n i ! ! = { ∏ i = 1 n 2 ( 2 i ) ! , n 为偶数 ∏ i = 1 n + 1 2 ( 2 i − 1 ) ! , n 为奇数 \prod\limits_{i=1}^n i!!=\begin{cases} \prod\limits_{i=1}^\frac{n}{2} (2i)! &,n为偶数 \\ \prod\limits_{i=1}^\frac{n+1}{2} (2i-1)! &,n为奇数 \end{cases} i=1∏ni!!=⎩ ⎨ ⎧i=1∏2n(2i)!i=1∏2n+1(2i−1)!,n为偶数,n为奇数
显而易见的,阶乘中因子 2 2 2 的个数一定多于因子 5 5 5 的个数,因此题目等价于求上式中因子 5 5 5 的个数//
考虑某单一阶乘 n ! n! n! 中所含因子 5 5 5 的个数。
可以发现,每个 5 5 5 的倍数项会提供 1 1 1 个因子 5 5 5 ,共有 ⌊ n 5 ⌋ \lfloor \dfrac{n}{5} \rfloor ⌊5n⌋ 项
除此之外每个 25 = 5 2 25=5^2 25=52 的倍数项会额外提供一个因子 5 5 5 ,共有 ⌊ n 5 2 ⌋ \lfloor \dfrac{n}{5^2} \rfloor ⌊52n⌋ 项
再除此之外每个 125 = 5 3 125=5^3 125=53 的倍数项会额外提供一个因子 5 5 5 ,共有 ⌊ n 5 3 ⌋ \lfloor \dfrac{n}{5^3} \rfloor ⌊53n⌋ 项……
因此对于单一阶乘 n ! n! n! ,其提供因子 5 5 5 的数量 c n t 5 = ∑ i = 1 N ⌊ n 5 i ⌋ ( 5 N > n ) cnt_5=\sum\limits_{i=1}^N \lfloor \dfrac{n}{5^i} \rfloor (5^N>n) cnt5=i=1∑N⌊5in⌋(5N>n)
接着考虑连乘积中因子 5 5 5 个数的总和。
a n s = { ∑ i = 1 n 2 ∑ j = 1 N ⌊ 2 i 5 j ⌋ = ∑ i = 1 N ∑ j = 1 n 2 ⌊ 2 j 5 i ⌋ , n 为偶数 ∑ i = 1 n + 1 2 ∑ j = 1 N ⌊ 2 i − 1 5 j ⌋ = ∑ i = 1 N ∑ j = 1 n + 1 2 ⌊ 2 j − 1 5 i ⌋ , n 为奇数 ans=\begin{cases} \sum\limits_{i=1}^\frac{n}{2} \sum\limits_{j=1}^N \lfloor \dfrac{2i}{5^j} \rfloor=\sum\limits_{i=1}^N \sum\limits_{j=1}^\frac{n}{2} \lfloor \dfrac{2j}{5^i} \rfloor &,n为偶数 \\ \sum\limits_{i=1}^\frac{n+1}{2} \sum\limits_{j=1}^N \lfloor \dfrac{2i-1}{5^j} \rfloor=\sum\limits_{i=1}^N \sum\limits_{j=1}^\frac{n+1}{2} \lfloor \dfrac{2j-1}{5^i} \rfloor &,n为奇数 \end{cases} \\ ans=⎩ ⎨ ⎧i=1∑2nj=1∑N⌊5j2i⌋=i=1∑Nj=1∑2n⌊5i2j⌋i=1∑2n+1j=1∑N⌊5j2i−1⌋=i=1∑Nj=1∑2n+1⌊5i2j−1⌋,n为偶数,n为奇数
对于某一 i i i ,发现不论 n n n 的奇偶, j = 1 j=1 j=1 开始的每 5 i 5^i 5i 项之和构成公差为 2 × 5 i 2\times5^i 2×5i 的等差数列//
例: i = 1 i=1 i=1 , n n n 为偶数且足够大时, ⌊ 2 j 5 i ⌋ \lfloor \dfrac{2j}{5^i} \rfloor ⌊5i2j⌋ 的前 15 15 15 项如下,其中每 5 5 5 项之和构成公差为 5 × 2 5\times 2 5×2 的等差数列: 0 , 0 , 1 , 1 , 2 ∣ ∣ 2 , 2 , 3 , 3 , 4 ∣ ∣ 4 , 4 , 5 , 5 , 6 … … 0,0,1,1,2||2,2,3,3,4||4,4,5,5,6…… 0,0,1,1,2∣∣2,2,3,3,4∣∣4,4,5,5,6……
经计算,对于某一 i i i ,等差数列的首项为
a 1 = { ⌊ 5 i 2 ⌋ + 2 , n 为偶数 ⌊ 5 i 2 ⌋ + 1 , n 为奇数 a_1=\begin{cases} \lfloor \dfrac{5^i}{2} \rfloor+2 &,n为偶数 \\ \lfloor \dfrac{5^i}{2} \rfloor+1 &,n为奇数 \end{cases} a1=⎩ ⎨ ⎧⌊25i⌋+2⌊25i⌋+1,n为偶数,n为奇数
完整的段用等差数列求和,非完整的段手算一下//
若此前完整段的数量记为 m m m ,则非完整段:
前 ⌊ 5 i 2 ⌋ \lfloor \dfrac{5^i}{2} \rfloor ⌊25i⌋ 项的值为 2 m 2m 2m ,
第 ⌊ 5 i 2 ⌋ + 1 \lfloor \dfrac{5^i}{2} \rfloor+1 ⌊25i⌋+1 至 $2\times\lfloor \dfrac{5^i}{2} \rfloor $ 项的值为 2 m + 1 2m+1 2m+1(手搓一下就知道了)
求和即可
令 N = ⌊ log 5 n ⌋ + 1 N=\lfloor \log_5n \rfloor+1 N=⌊log5n⌋+1 ,对 i ∈ [ 1 , N ] i\in[1,N] i∈[1,N] 遍历求和得到答案
由于答案数据极其庞大,超出了C++ %lld(64bits)的范围,因此需要使用更高位数的整数类型(如int128)//或者直接转战Python
时间复杂度
O ( log n ) O(\log n) O(logn)
参考代码
import math
# while 1:
n=int(input())
N=int(math.log(n,5)+1)
re=0
if n%2==0 :for i in range(1,N+1) :#print("i="+str(i))a1=(5**i)//2+2 #首项#print("a1="+str(a1))d=(5**i)*2 #公差#print("d="+str(d))m=(n//2)//(5**i) #完整段数#print("m="+str(m))re+=(2*a1+(m-1)*d)*m//2 #完整段等差数列求和#print("re1:" + str(re))re+=(n//2-m*(5**i))*2*m #最后一段余项求和#print("re2:" + str(re))#print("pl1=" + str((n//2-m*(5**i))*2*m))if n//2-m*(5**i)>(5**i)//2 :re+=n//2-m*(5**i)-(5**i)//2#print("pl2=" + str(n//2-m*(5**i)-(5**i)//2))if n%2 :for i in range(1,N+1) :#print("i="+str(i))a1=(5**i)//2+1 #首项#print("a1="+str(a1))d=(5**i)*2 #公差#print("d="+str(d))m=((n+1)//2)//(5**i) #完整段数#print("m="+str(m))re+=(2*a1+(m-1)*d)*m//2 #完整段等差数列求和#print("re1:" + str(re))re+=((n+1)//2-m*(5**i))*2*m #最后一段余项求和#print("re2:" + str(re)) #print("pl1=" + str(((n+1)//2-m*(5**i))*2*m))if (n+1)//2-m*(5**i)>(5**i)//2 :re+=(n+1)//2-m*(5**i)-(5**i)//2#print("pl2=" + str((n+1)//2-m*(5**i)-(5**i)//2))print(re)
相关文章:

题解 | #C.idol!!# 2023牛客暑期多校6
C.idol!! 数学 题目大意 正整数 n n n 的双阶乘 n ! ! n!! n!! 表示不超过 n n n 且与 n n n 有相同奇偶性的所有正整数乘积 求对于给定 n n n , ∏ i 1 n i ! ! \prod\limits_{i1}^n i!! i1∏ni!! 的后缀 0 0 0 个数 解题思路 根据双阶乘的性质&…...

使用filebeat收集并解析springboot日志
序 本文主要研究一下如何使用filebeat收集并解析springboot日志 安装 在官网的下载页面filebeat/downloads提供了一些特定平台的安装包,不过对应linux最为省事的安装方式就是直接下载x86_64压缩包,然后解压即可 wget https://artifacts.elastic.co/d…...

P1993 小 K 的农场
小 K 的农场 题目描述 小 K 在 MC 里面建立很多很多的农场,总共 n n n 个,以至于他自己都忘记了每个农场中种植作物的具体数量了,他只记得一些含糊的信息(共 m m m 个),以下列三种形式描述:…...
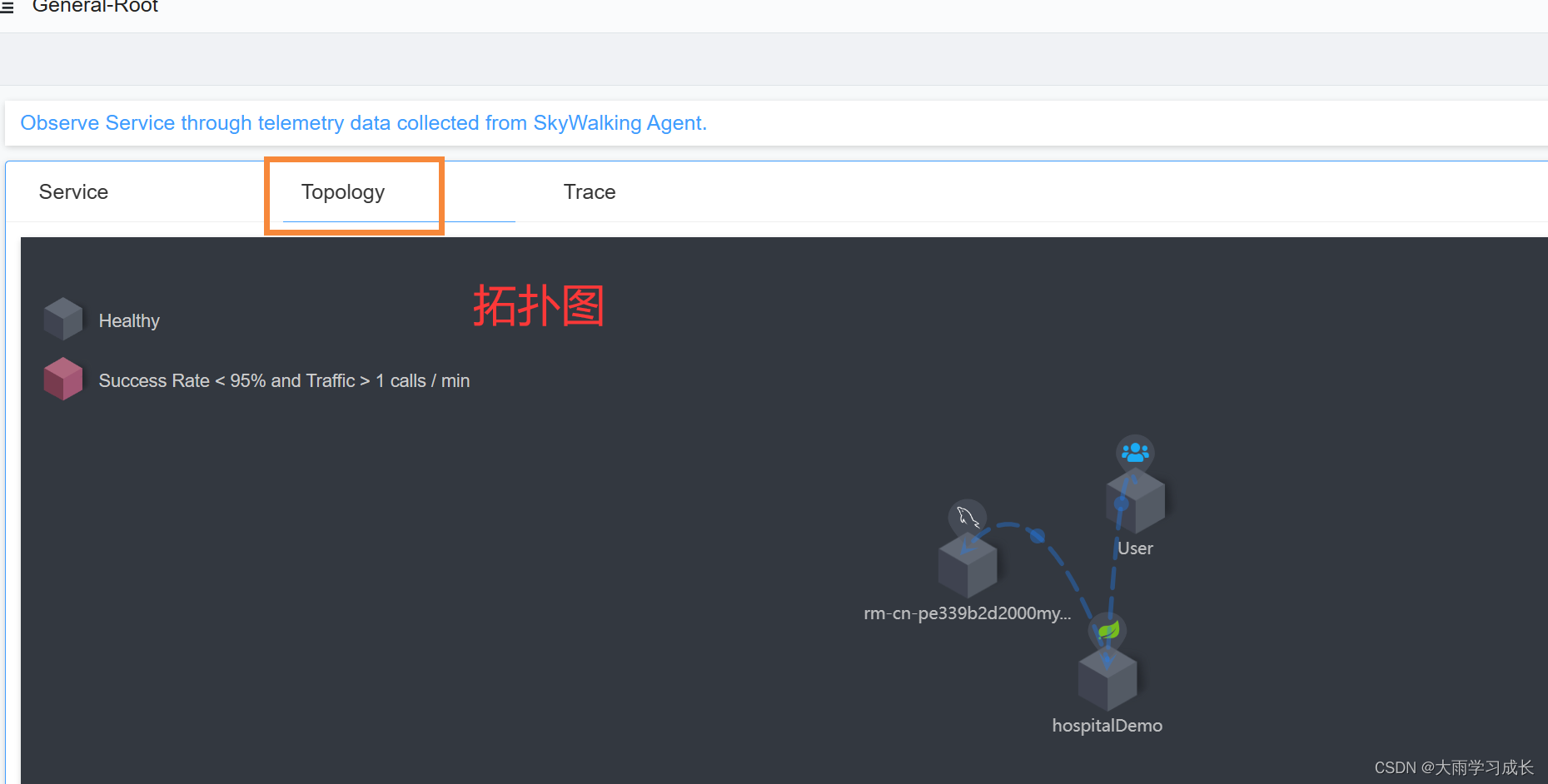
Spring boot 集成 Skywalking 配置 || Skywalking 打不开【已解决】
一、Skywalking官网 Apache SkyWalking 1.下载Skywalking APM (如果下载最新的,双击打开闪退,选老点的版本) 2. 下载 Skywalking Agents 如果下载太慢,建议复制下载链接,然后用下载器下载,比…...

手把手教你使用 ftrace 对 Linux 系统进行 debug
1、简介 strace:用来跟踪 Linux 进程执行时的系统调用和接收所接收的信号,可以跟踪到一个进程产生的系统调用,包括参数,返回值,执行消耗的时间。 ftrace:是一个 Linux 内核函数跟踪器,function tracer,旨在帮助开发人员和系统设计者可以找到内核内部发生的事情,从 L…...
【练】要求定义一个全局变量 char buf[] = “1234567“,创建两个线程,不考虑退出条件,打印buf
要求定义一个全局变量 char buf[] "1234567",创建两个线程,不考虑退出条件,另: A线程循环打印buf字符串,B线程循环倒置buf字符串,即buf中本来存储1234567,倒置后buf中存储7654321. 不…...

iOS Viper架构(中文版)【看懂这篇就够了】
完整源码地址 一、iOS_Viper iOS的Viper架构,作为一个从业多年的iOS开发者,我个人认为应该要会一点viper 二、前言 viper的设计模式在iOS开发中不流行,甚至是Swift中,也没有用,我认为比较可惜。作为iOSer,当你掌握…...

深入理解缓存 TLB 原理
今天分享一篇TLB的好文章,希望大家夯实基本功,让我们一起深入理解计算机系统。 TLB 是 translation lookaside buffer 的简称。首先,我们知道 MMU 的作用是把虚拟地址转换成物理地址。 MMU工作原理 虚拟地址和物理地址的映射关系存储在页表…...

获取k8s scale资源对象的命令
kubectl get --raw /apis/<apiGroup>/<apiVersion>/namespaces/<namespaceName>/<resourceKind>/<resourceName>/scale 说明:scale资源对象用来水平扩展k8s资源对象的副本数,它是作为一种k8s资源对象的子资源存在…...

基于ChatYuan-large-v2 语言模型 Fine-tuning 微调训练 广告生成 任务
一、ChatYuan-large-v2 ChatYuan-large-v2是一个开源的支持中英双语的功能型对话语言大模型,与其他 LLM 不同的是模型十分轻量化,并且在轻量化的同时效果相对还不错,仅仅通过0.7B参数量就可以实现10B模型的基础效果,正是其如此的…...
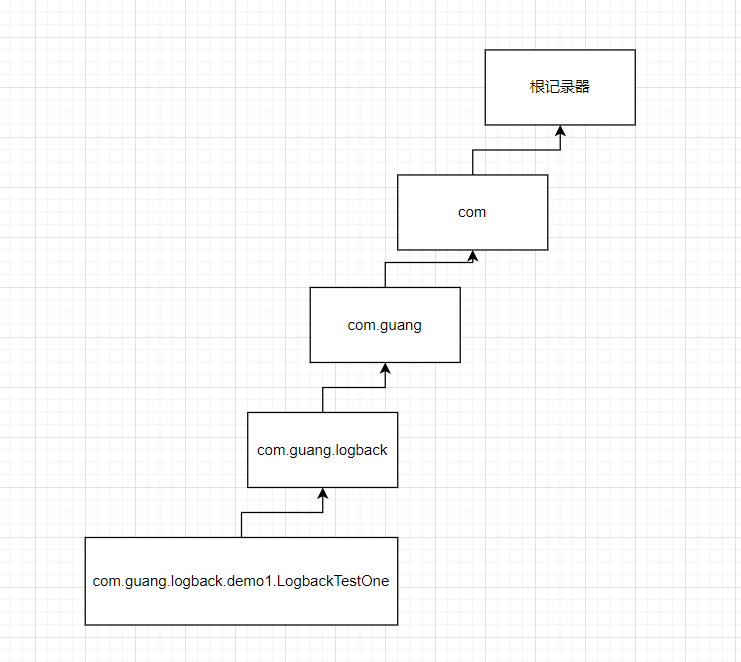
SpringBoot集成Logback日志
SpringBoot集成Logback日志 文章目录 SpringBoot集成Logback日志一、什么是日志二、Logback简单介绍三、SpringBoot项目中使用Logback四、概念介绍一、日志记录器Logger1.1、日志记录器对象生成1.2、记录器的层级结构1.3、过滤器1.4、logger设置日志级别1.5、java代码演示1.6、…...
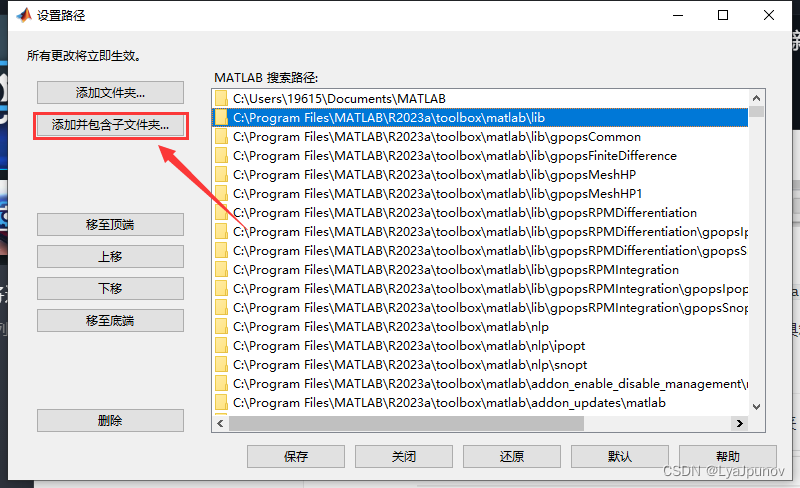
MATLAB(R2023a)添加工具箱TooLbox的方法-以GPOPS为例
一、找到工具箱存放位置 首先我们需要找到工具箱的存放位置,点击这个设置路径可以看到 我们的matlab工具箱的存放位置 C:\Program Files\MATLAB\R2023a\toolbox\matlab 从资源管理器中打开这个位置,可以看到里面各种工具箱 二、放入工具箱 解压我们…...
助力618-Y的混沌实践之路 | 京东云技术团队
一、写在前面 1、混沌是什么? 混沌工程(Chaos Engineering)的概念由 Netflix 在 2010 年提出,通过主动向系统中引入异常状态,并根据系统在各种压力下的行为表现确定优化策略,是保障系统稳定性的新型手段。…...

Python系统学习1-4-物理行、逻辑行、选择语句
一、行 (1) 物理行:程序员编写代码的行。 (2) 逻辑行:python解释器需要执行的指令。 (3) 建议: 一个逻辑行在一个物理行上。 如果一个物理行中使用多个逻辑行,需要使用分号;隔开。 (4) 换行: 如果…...
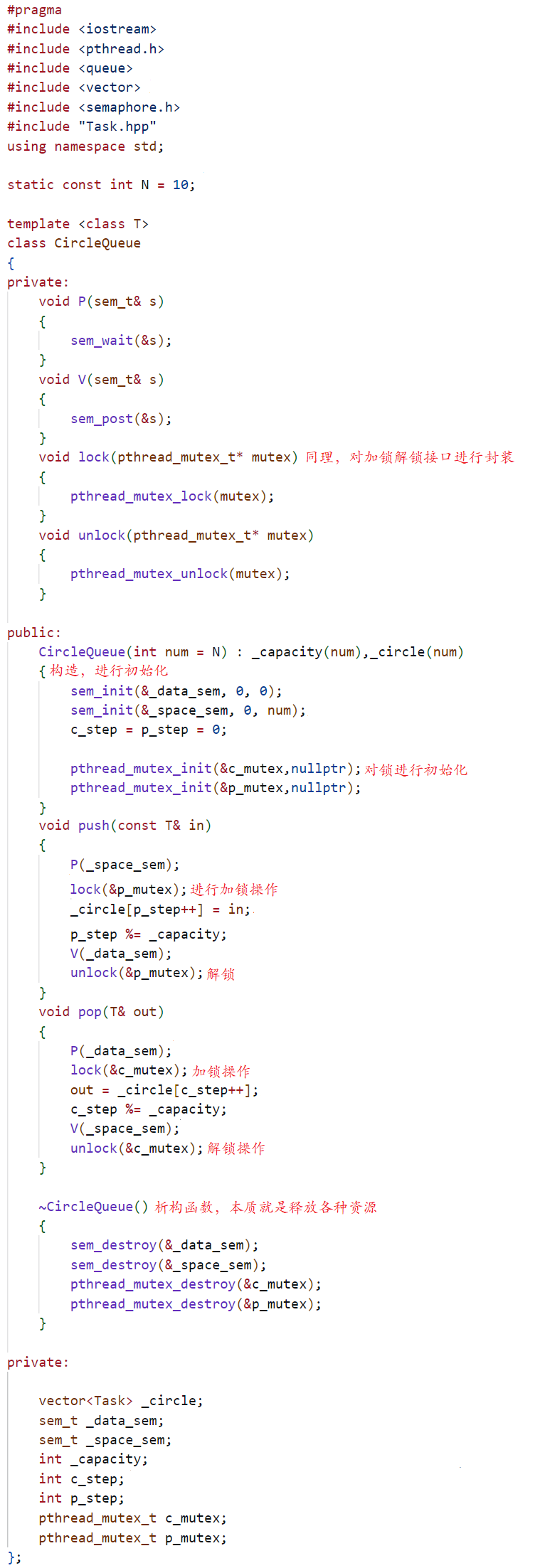
学习系统编程No.35【基于信号量的CP问题】
引言: 北京时间:2023/8/2/12:52,时间飞逝,恍惚间已经来到了八月,给我的第一感觉就是快开学了,别的感觉其实没有,哈哈!看着身边的好友网络相关知识都要全部学完了,就好像…...
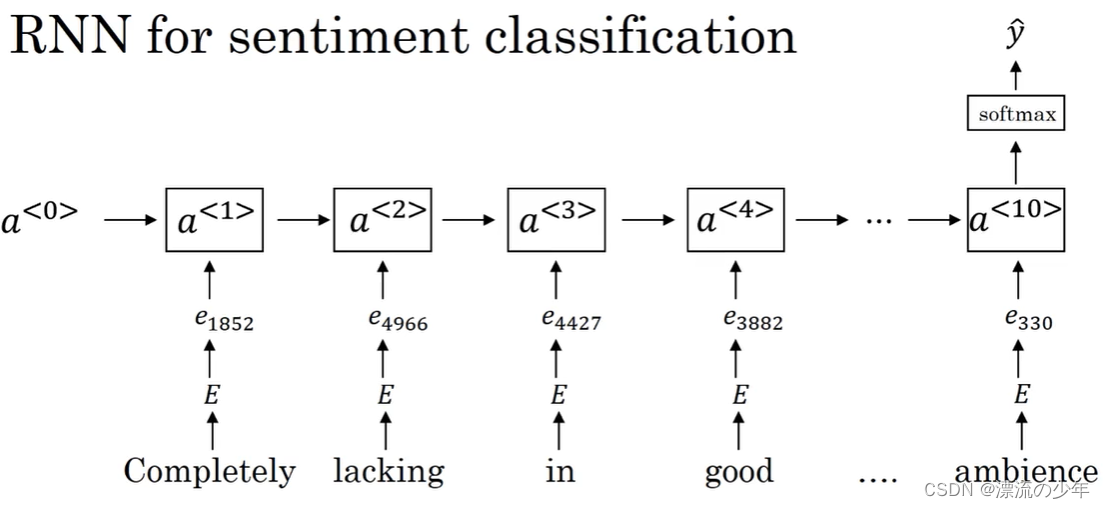
词嵌入、情感分类任务
目录 1.词嵌入(word embedding) 对单词使用one-hot编码的缺点是难以看出词与词之间的关系。 所以需要使用更加特征化的表示(featurized representation),如下图所示,我们可以得到每个词的向量表达。 假设…...

TypeScript使用技巧
文章目录 使用技巧TypeScript内置的工具类型keyofextends 限定泛型interface 与 type 区别 TypeScript作为JavaScript的超集,通过提供静态类型系统和对ES6新特性的支持,使JavaScript开发变得更加高效和可维护。掌握TypeScript的使用技巧,可以帮助我们更好地开发和组织JavaScrip…...
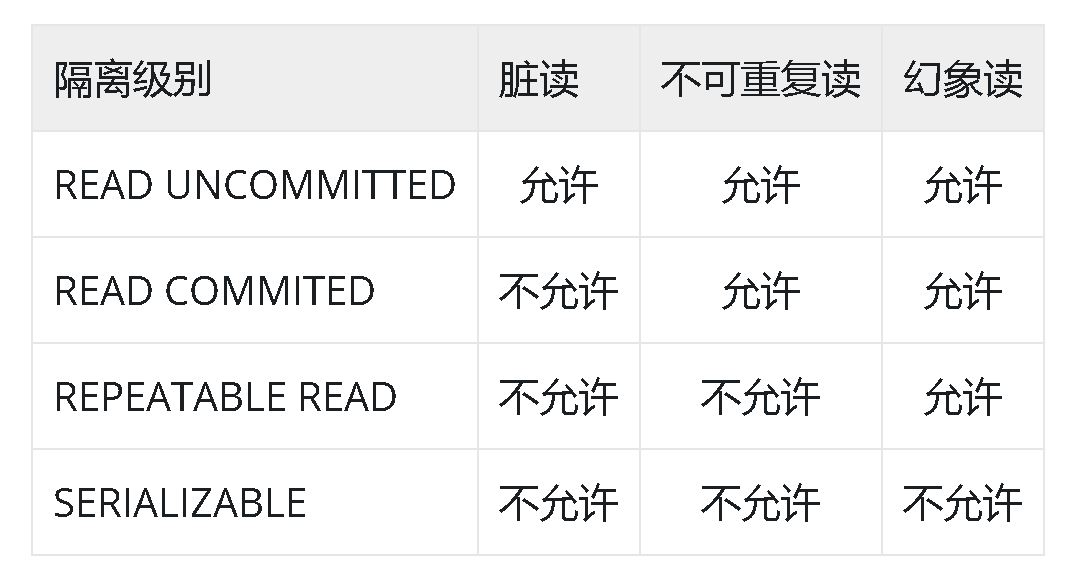
MySQL — InnoDB事务
文章目录 事务定义事务特性事务隔离级别READ UNCOMMITTEDREPEATABLE READREAD COMMITTEDSERIALIZABLE 事务存在的问题脏读(Dirty Read)不可重复读(Non-repeatable Read)幻读(Phantom Read) 事务定义 数据库…...
LeetCode 42. 接雨水(动态规划 / 单调栈)
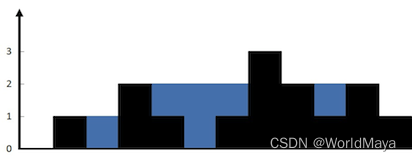
题目: 链接:LeetCode 42. 接雨水 难度:困难 给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。 示例 1: 输入:height [0,1,0,2,1,0,1,3,2,1,2…...

顺序表、链表刷题指南(力扣OJ)
目录 前言 题目一:删除有序数组中的重复项 思路: 题解: 题目二:合并两个有序数组 思路: 分析: 题解: 题目三:反转链表 思路: 分析: 题解: 题目四&…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...

数据结构第5章:树和二叉树完全指南(自整理详细图文笔记)
名人说:莫道桑榆晚,为霞尚满天。——刘禹锡(刘梦得,诗豪) 原创笔记:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 上一篇:《数据结构第4章 数组和广义表》…...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...
