排序进行曲-v2.0
小程一言
这篇文章是在排序进行曲1.0之后的续讲,
由于在上一篇讲的排序的基本概念与分类,所以这篇主要是对几个
简单的排序进行细致的分析,有直接插入排序、希尔排序以及堆排序。
直接插入排序
直接插入排序是一种简单直观的排序算法,它的基本思想是将待排序的元素依次插入到已排序的序列中的合适
位置,从而逐步形成有序序列。
步骤
1、将待排序的元素序列分为已排序区和未排序区。一开始已排序区只有一个元素,就是待排序序列的第一个元素。
2、从未排序区取出第一个元素,将其与已排序区的元素逐个比较,找到合适的位置插入。
3、比较的过程是从已排序区的最后一个元素开始,如果该元素大于待插入元素,则将该元素后移一位,直到找到一个小于等于待插入元素的元素位置。
4、将待插入元素插入到找到的位置后,已排序区的元素个数加一。
5、重复步骤2~4,直到未排序区的元素全部插入到已排序区。
举例
原始序列:5 3 8 6 4第一轮插入:3 5 8 6 4第二轮插入:3 5 6 8 4第三轮插入:3 4 5 6 8通过例子可以看出,直接插入排序每次将一个元素插入到已排序序列中的合适位置,通过不断地插入操作,最终将序列排序完成。
复杂度分析
直接插入排序的时间复杂度为O(n^2),其中n是待排序序列的长度。直接插入排序的最好情况时间复杂度为O(n),即当待排序序列已经有序时,只需要比较n-1次即可完成排序。最坏情况时间复杂度为O(n^2),即当待排序序列逆序排列时,需要比较和移动的次数最多。平均情况下,直接插入排序的时间复杂度也是O(n^2)。直接插入排序的空间复杂度为O(1),即只需要常数级别的额外空间。直接插入排序是一种稳定的排序算法,即相等元素的相对顺序在排序前后不会改变。
应用场景
小规模数据排序:直接插入排序对于小规模的数据排序效果较好,因为它的时间复杂度为O(n^2),在数据规模较小的情况下,其性能优于其他复杂度较高的排序算法。例如,对于一个包含100个元素的数组进行排序,直接插入排序的效率较高。部分有序数据排序:如果待排序的数据已经部分有序,即每个元素距离它的最终位置不远,那么直接插入排序的效果会很好。这是因为直接插入排序每次将一个元素插入到已经有序的部分中,插入的操作比较快速。例如,对于一个近乎有序的数组进行排序,直接插入排序的效率较高。数据量较小且基本有序的在线排序:直接插入排序可以在不断接收新数据的情况下,实时对数据进行排序。例如,一个在线的股票交易系统,需要对新到达的交易数据进行排序,直接插入排序可以满足实时性的要求。
实际举例
假设有一个学生成绩的数组,需要按照成绩从低到高进行排序。可以使用直接插入排序来实现。首先,将第一个元素视为有序的部分,然后从第二个元素开始,逐个将元素插入到已经有序的部分中。具体的操作是,从第二个元素开始,将其与已经有序的部分比较,找到合适的位置插入,然后再将下一个元素插入,直到所有元素都被插入完成。这样就可以得到按照成绩从低到高排序的数组。
代码实现
public class InsertionSort {public static void main(String[] args) {int[] arr = {5, 2, 8, 3, 1};insertionSort(arr);for (int num : arr) {System.out.print(num + " ");}}public static void insertionSort(int[] arr) {int n = arr.length;for (int i = 1; i < n; i++) {int key = arr[i];int j = i - 1;while (j >= 0 && arr[j] > key) {arr[j + 1] = arr[j];j--;}arr[j + 1] = key;}}
}

希尔排序
希尔排序(Shell Sort)是插入排序的一种改进算法,也被称为缩小增量排序。希尔排序通过将待排序的元素按照一定的间隔分组,对每组进行插入排序,然后逐渐减小间隔,直到间隔为1时进行最后一次插入排序。
步骤
1、初始化间隔gap的值为数组长度的一半,然后不断将gap缩小为原来的一半,直到gap为1。
2、对于每个gap,将数组分为gap个子序列,分别对每个子序列进行插入排序。
3、在每个子序列中,从第gap个元素开始,依次与前面的元素比较,如果前面的元素较大,则将其后移gap个位置,直到找到合适的位置插入当前元素。
4、继续对每个子序列进行插入排序,直到所有子序列都排好序。
5、缩小gap的值为原来的一半,重复步骤2-4,直到gap为1时完成排序。
举例
假设有一个数组 [9, 5, 7, 1, 3],我们将使用希尔排序对其进行排序。首先,选择一个增量(gap),可以是数组长度的一半。在这个例子中,数组长度为5,所以我们选择增量为2。然后,我们将数组分为若干个子数组,每个子数组相隔增量个元素。对于这个例子,我们将数组分为两个子数组:[9, 7, 3] 和 [5, 1]。接下来,对每个子数组进行插入排序。在插入排序中,我们将每个元素与它前面的元素进行比较,并将它插入到正确的位置。对于这个例子,我们得到以下两个子数组:[3, 7, 9] 和 [1, 5]。然后,我们将增量减小一半,即变为1。此时,我们将整个数组作为一个子数组进行插入排序。对于这个例子,我们得到最终的排序结果:[1, 3, 5, 7, 9]。
复杂度分析
希尔排序是一种改进的插入排序算法,它通过将数组分成多个子序列进行排序,然后逐步缩小子序列的长度,最终使整个数组有序。希尔排序的时间复杂度取决于步长序列的选择。常用的步长序列有希尔增量序列和Hibbard增量序列。希尔增量序列是将数组长度不断除以2得到的序列,直到序列的最后一个元素为1。例如,对于一个长度为N的数组,希尔增量序列可以是N/2, N/4, N/8, ..., 1。Hibbard增量序列是将2^k - 1作为步长,其中k从1开始递增,直到2^k - 1大于等于数组长度N。例如,对于一个长度为N的数组,Hibbard增量序列可以是1, 3, 7, 15, ..., 2^k - 1。希尔排序的平均时间复杂度为O(n^1.3),其中n是数组的长度。这个时间复杂度是基于希尔增量序列的选择得出的。然而,希尔排序的时间复杂度并不是确定的,它可能会受到输入数据的影响。对于某些特定的输入数据,希尔排序的时间复杂度可能会更低,甚至接近O(n)。这是因为希尔排序在每一轮排序中,对于相隔较远的元素进行了交换,从而提前将较小或较大的元素移动到了正确的位置,减少了后续排序的次数。总结起来,希尔排序的时间复杂度是不确定的,但平均情况下为O(n^1.3)。
应用场景
数组规模较大:希尔排序在大规模数组排序时具有较好的性能表现,比如对百万级别的数据进行排序。数据分布较均匀:希尔排序对于数据分布较均匀的情况下,排序效率较高。如果数据分布不均匀,可能会导致排序效率下降。对稳定性没有要求:希尔排序是一种不稳定的排序算法,即相同元素的相对位置可能会发生变化。如果对排序结果的稳定性有要求,不适合使用希尔排序。对内存空间要求较低:希尔排序是一种原地排序算法,不需要额外的内存空间,适合在内存空间有限的情况下使用。
实际举例
排序算法:希尔排序可以用于对大规模数据进行排序,尤其是在数据量较大且无序程度较高的情况下,相比于其他排序算法,希尔排序具有较高的效率。数据库索引:在数据库中,索引是对表中的数据进行快速查找的一种数据结构。希尔排序可以用于对索引进行排序,提高数据库查询的效率。编程语言中的排序函数:许多编程语言中的排序函数底层实现使用了希尔排序算法,例如C++中的std::sort函数就是使用希尔排序作为默认实现。数据压缩:希尔排序可以用于对数据进行压缩,通过对数据进行排序,可以使得相同的数据连续出现,从而提高数据的压缩率。图像处理:希尔排序可以用于对图像进行排序,例如对像素点的颜色值进行排序,从而实现图像的特效处理。
代码实现
public class ShellSort {public static void shellSort(int[] arr) {int n = arr.length;for (int gap = n / 2; gap > 0; gap /= 2) {for (int i = gap; i < n; i++) {int temp = arr[i];int j = i;while (j >= gap && arr[j - gap] > temp) {arr[j] = arr[j - gap];j -= gap;}arr[j] = temp;}}}public static void main(String[] args) {int[] arr = {9, 5, 2, 7, 1, 8, 6, 3, 4};shellSort(arr);System.out.println("排序结果:");for (int num : arr) {System.out.print(num + " ");}}
}//排序结果:1 2 3 4 5 6 7 8 9
堆排序
堆排序是一种基于堆数据结构的排序算法,它的时间复杂度为O(nlogn)。堆排序的基本思想是将待排序的序列构建成一个大顶堆(或小顶堆),然后依次将堆顶元素与最后一个元素交换,再重新调整堆,重复这个过程直到整个序列有序。
步骤
堆排序是一种基于二叉堆的排序算法,1、构建最大堆(或最小堆):将待排序的数组看作是一个完全二叉树,根据堆的性质,可以通过从最后一个非叶子节点开始,依次向上调整每个节点,使得每个节点都满足堆的性质。这样就可以得到一个最大堆(或最小堆)。2、将堆顶元素与最后一个元素交换:将最大堆(或最小堆)的堆顶元素与数组的最后一个元素交换位置,这样最大(或最小)的元素就被放到了最后的位置。3、调整堆:将交换后的堆顶元素向下调整,使得堆的性质仍然成立。具体操作是将堆顶元素与其左右子节点中较大(或较小)的元素交换位置,然后继续向下调整交换后的节点,直到堆的性质满足。4、重复步骤2和步骤3直到完成排序:重复执行步骤2和步骤3,每次都将堆顶元素与当前未排序的部分的最后一个元素交换,并调整堆,直到所有元素都被交换到了正确的位置。这样就完成了堆排序。
举例
待排序序列:[4, 10, 3, 5, 1]建堆:从最后一个非叶子节点开始,依次向上调整,使得每个节点的值都大于等于其子节点的值。调整后的堆为:[10, 5, 3, 4, 1]排序:将堆顶元素10与最后一个元素1交换位置,并将堆的大小减1。交换后的堆为:[1, 5, 3, 4]。然后再对堆顶元素1进行一次向下调整,使得堆重新满足堆的定义。调整后的堆为:[5, 4, 3, 1]。再次排序:将堆顶元素5与最后一个元素1交换位置,并将堆的大小减1。交换后的堆为:[1, 4, 3]。然后再对堆顶元素1进行一次向下调整,使得堆重新满足堆的定义。调整后的堆为:[4, 1, 3]。再次排序:将堆顶元素4与最后一个元素3交换位置,并将堆的大小减1。交换后的堆为:[3, 1]。然后再对堆顶元素3进行一次向下调整,使得堆重新满足堆的定义。调整后的堆为:[1, 3]。最后排序:将堆顶元素1与最后一个元素3交换位置,并将堆的大小减1。交换后的堆为:[3]。堆的大小为1,排序完成。
最终排序结果:[1, 3, 4, 5, 10]
复杂度分析
建堆:建堆的时间复杂度为O(n),其中n为待排序序列的长度。调整堆:调整堆的时间复杂度为O(logn)。在堆排序过程中,需要调整堆的次数为n-1次,每次调整堆的时间复杂度为O(logn)。堆排序:堆排序的时间复杂度为O(nlogn)。在堆排序过程中,需要进行n-1次调整堆的操作,每次调整堆的时间复杂度为O(logn)。因此,堆排序的总时间复杂度为O(nlogn)。综上所述,堆排序的时间复杂度为O(nlogn)。
应用场景
需要对大量数据进行排序的场景,堆排序的时间复杂度为O(nlogn),效率较高。需要稳定性较差的排序算法,堆排序是一种不稳定的排序算法,适用于不要求相同元素的相对位置保持不变的场景。需要对数据进行动态排序的场景,堆排序可以在不断插入新元素的情况下,快速对数据进行排序。需要找出最大或最小的前k个元素的场景,堆排序可以通过构建最大堆或最小堆,快速找到最大或最小的元素。
实际举例
优先级队列:堆排序可以用于实现优先级队列,其中每个元素都有一个优先级。通过使用最大堆,可以确保优先级最高的元素始终位于堆的根节点,从而可以快速找到并删除具有最高优先级的元素。任务调度:在任务调度中,每个任务都有一个优先级和执行时间。通过使用最小堆,可以按照任务的优先级和执行时间对任务进行排序,从而实现高效的任务调度。多路归并排序:堆排序可以用于多路归并排序,其中有多个有序序列需要合并成一个有序序列。通过使用最小堆,可以选择每个有序序列的最小元素进行合并,从而实现高效的多路归并排序。求Top K问题:在一组数据中,找到最大或最小的K个元素。通过使用最大堆,可以维护一个大小为K的堆,每次从数据中取出一个元素与堆顶元素比较,如果比堆顶元素大,则替换堆顶元素并重新调整堆,最终堆中的元素就是最大的K个元素。中位数问题:在一组数据中,找到中间位置的元素。通过使用最大堆和最小堆,可以将数据分为两部分,其中最大堆存储较小的一半数据,最小堆存储较大的一半数据。这样可以快速找到中位数,并支持动态添加和删除元素。代码实现
public class HeapSort {public void heapSort(int[] arr) {int n = arr.length;// 建立最大堆for (int i = n / 2 - 1; i >= 0; i--)heapify(arr, n, i);// 逐个将堆顶元素移到数组末尾for (int i = n - 1; i >= 0; i--) {// 将当前堆顶元素(最大值)与数组末尾元素交换int temp = arr[0];arr[0] = arr[i];arr[i] = temp;// 重新调整堆,找出剩下元素的最大值heapify(arr, i, 0);}}// 调整堆void heapify(int[] arr, int n, int i) {int largest = i; // 初始化最大值为根节点int left = 2 * i + 1; // 左子节点int right = 2 * i + 2; // 右子节点// 如果左子节点大于根节点,将最大值设为左子节点if (left < n && arr[left] > arr[largest])largest = left;// 如果右子节点大于当前最大值,将最大值设为右子节点if (right < n && arr[right] > arr[largest])largest = right;// 如果最大值不是根节点,交换根节点与最大值,并继续调整堆if (largest != i) {int swap = arr[i];arr[i] = arr[largest];arr[largest] = swap;heapify(arr, n, largest);}}// 测试代码public static void main(String[] args) {int[] arr = {9, 5, 2, 7, 1, 8, 3};HeapSort heapSort = new HeapSort();heapSort.heapSort(arr);System.out.println("排序结果:");for (int num : arr) {System.out.print(num + " ");}}
}
//输出结果为:1 2 3 5 7 8 9。相关文章:

排序进行曲-v2.0
文章目录 小程一言直接插入排序步骤举例复杂度分析应用场景实际举例代码实现 希尔排序步骤举例复杂度分析应用场景实际举例代码实现 堆排序步骤举例复杂度分析应用场景实际举例代码实现 小程一言 这篇文章是在排序进行曲1.0之后的续讲, 由于在上一篇讲的排序的基本…...
反弹shell的N种姿势
预备知识1. 关于反弹shell 就是控制端监听在某TCP/UDP端口,被控端发起请求到该端口,并将其命令行的输入输出转到控制端。reverse shell与telnet,ssh等标准shell对应,本质上是网络概念的客户端与服务端的角色反转。2. 反弹shel…...
创意视频剪辑教程:快速合并视频并标题,让你的作品更吸睛!
想要让你的视频作品脱颖而出,引人注目?不再担心,我们为你带来了一款创意视频剪辑教程,教你如何快速合并视频并添加令人惊艳的标题效果!让你的作品在分钟内变得酷炫而精彩,向世界展示你的创意! …...
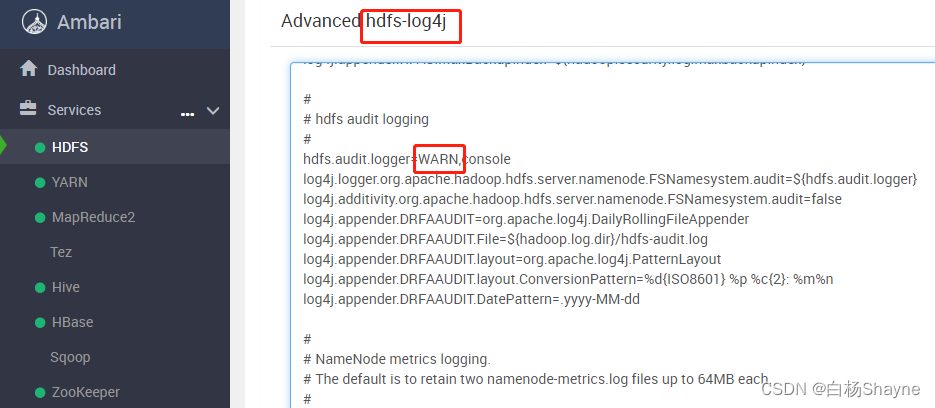
解决Hadoop审计日志hdfs-audit.log过大的问题
【背景】 新搭建的Hadoop环境没怎么用,就一个环境天天空跑,结果今天运维告诉我说有一台服务器磁盘超过80%了,真是太奇怪了,平台上就跑了几个spark测试程序,哪来的数据呢? 【问题调查】 既然是磁盘写满了&…...

【Java】java和kotlin关于Json写文件
Java写json文件 public class WriterJson {public static void main(String[] args) {// 创建一个 JSON 对象JSONObject jsonObject new JSONObject();jsonObject.put("case", "testtest");JSONObject jsonObjects new JSONObject();jsonObjects.put(&q…...
【深度学习】采用自动编码器生成新图像
一、说明 你知道什么会很酷吗?如果我们不需要所有这些标记的数据来训练 我们的模型。我的意思是标记和分类数据需要太多的工作。 不幸的是,大多数现有模型从支持向量机到卷积神经网,没有它们,卷积神经网络就无法训练。无监督学习不…...

华为云交付
文章目录 一、华为云-公有云架构华为公有云的主要服务1.华为云服务—计算类2.华为云服务——存储类3.华为云服务—网络类4.华为云服务—管理和监督类5.华为云数据库 二、待续 一、华为云-公有云架构 华为公有云的主要服务 ECS:弹性云服务器( Elastic Cl…...
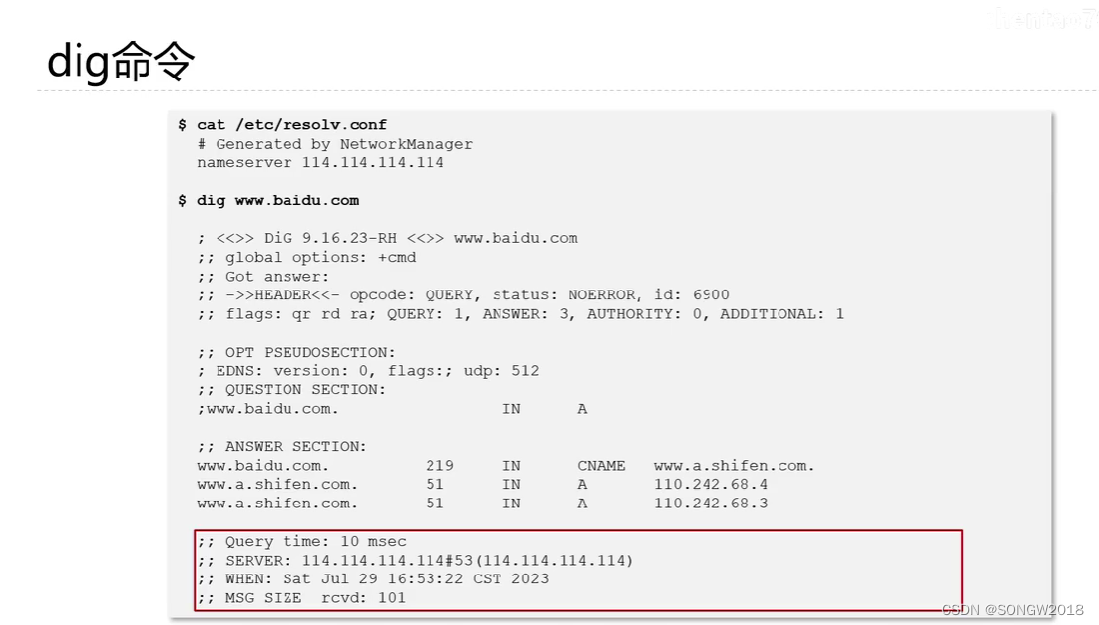
dns瞅一瞅
正向解析—域名到ip 反向解析–ip到域名 域名本身是从又往左来解释的 根域—最顶层的域,用null字符标识,通常会省略最后的点和null字符,但是应用程序会在解析dns之前添加这些字符 顶级域— 两种类型,一种国家、地区代码的顶级域…...
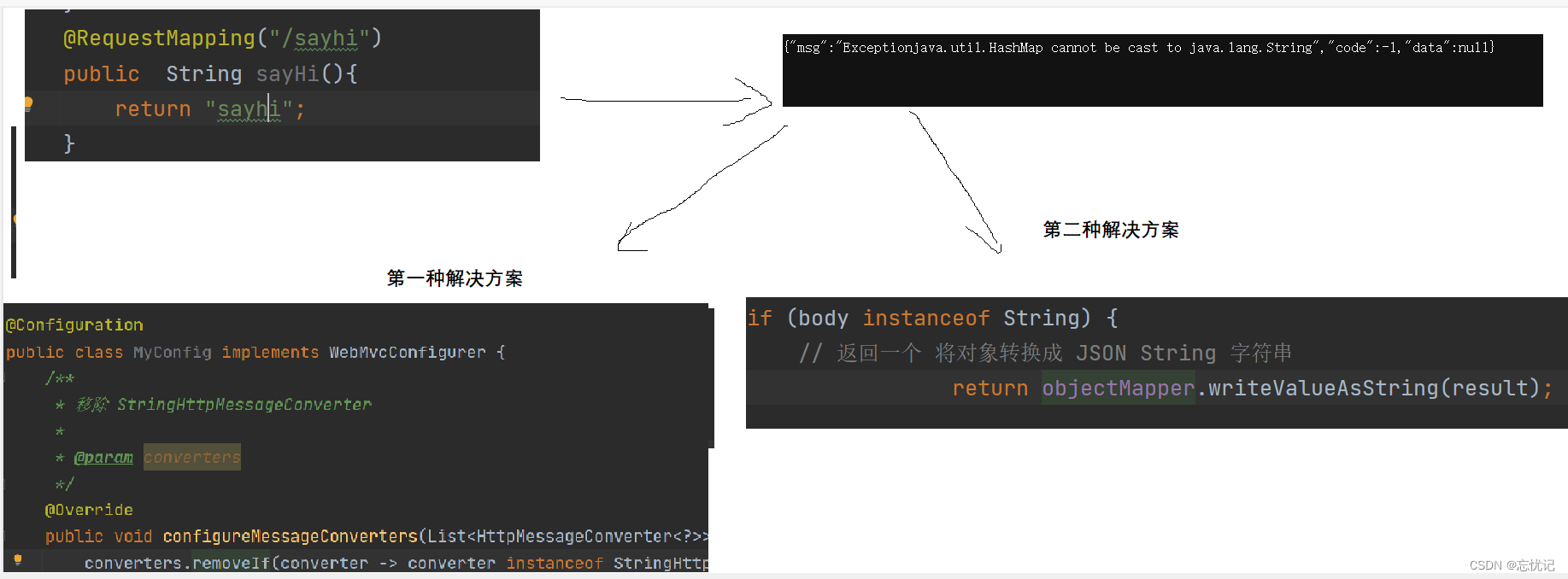
springAOP的实例
文章目录 前言一.用户登录权限校验1.1 spring 拦截器1.2 传统的用户登录权限验证1.3 使用拦截器的方式1.4 案例1.5 拦截器实现原理 三.统一异常处理3.1 什么是统一异常处理3.2 具体步骤 四.统⼀数据返回格式4.1 为什么需要统一的数据返回4.2 统一返回数据的格式4.3 统一移除处理…...
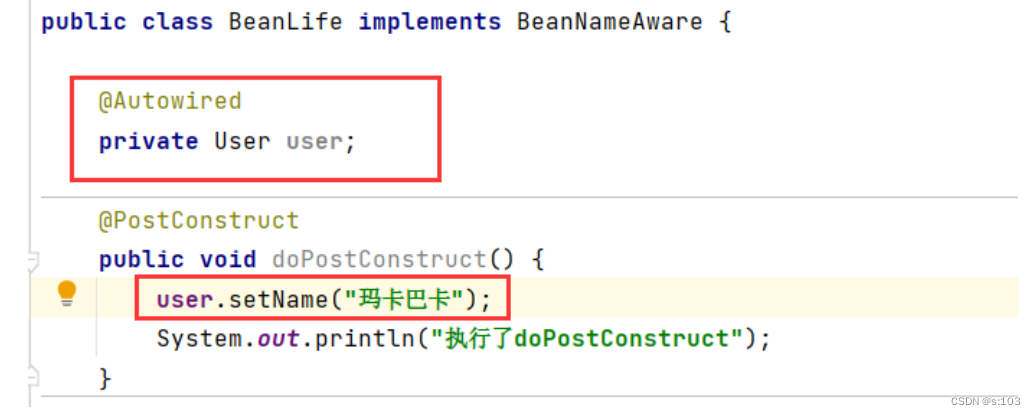
【JavaEE】深入了解Spring中Bean的可见范围(作用域)以及前世今生(生命周期)
【JavaEE】Spring的开发要点总结(4) 文章目录 【JavaEE】Spring的开发要点总结(4)1. Bean的作用域1.1 一个例子感受作用域的存在1.2 通过例子说明作用域的定义1.3 六种不同的作用域1.3.1 singleton单例模式(默认作用域…...
)
P1320 压缩技术(续集版)
题目描述 设某汉字由 N N N \times N NN 的 0 \texttt 0 0 和 1 \texttt 1 1 的点阵图案组成。 我们依照以下规则生成压缩码。连续一组数值:从汉字点阵图案的第一行第一个符号开始计算,按书写顺序从左到右,由上至下。第一个数表示连续有…...
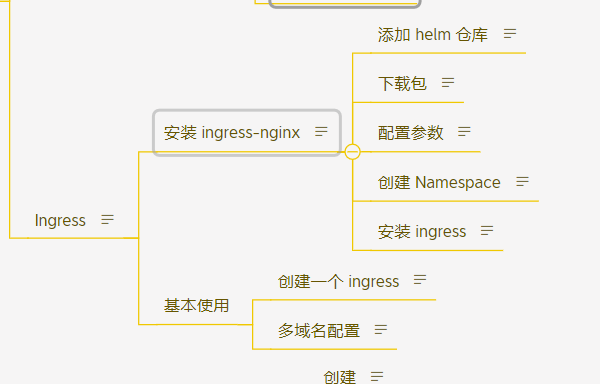
k8s(七) 叩丁狼 service Ingress
负责东西流量(同层级/内部服务网络通信)的通信 service的定义 apiVersion: v1 kind: Service metadata:name: nginx-svclabels:app: nginx-svc spec:ports:- name: http # service 端口配置的名称protocol: TCP # 端口绑定的协议,支持 TCP、…...
Android Studio 关于BottomNavigationView 无法预览视图我的解决办法
一、前言:最近在尝试一步一步开发一个自己的软件,刚开始遇到的问题就是当我们引用 com.google.android.material.bottomnavigation.BottomNavigationView出现了无法预览视图的现象,我也在网上查了很多中解决方法,最后在执行了如下…...
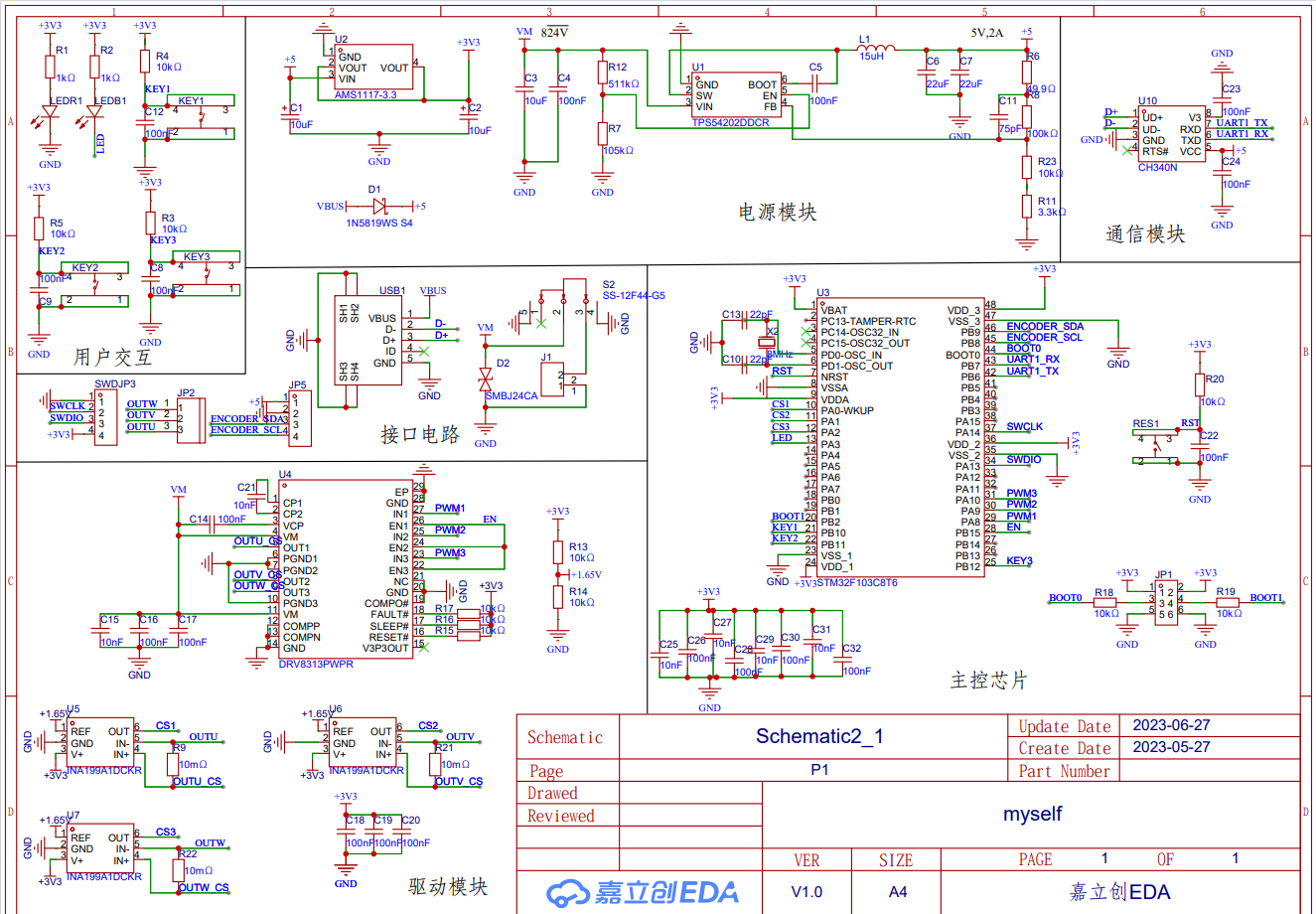
【STM32】小电流FOC驱控一体板(开源)
FOC驱控一体板 主控芯片stm32f103c8t6 驱动芯片drv8313 三相电流采样 根据B站一个UP主的改的(【【自制】年轻人的第一块FOC驱动器】),大多数元器件是0805,实验室具备且便于自己动手焊接 。 晶振用的是无源晶振,体…...
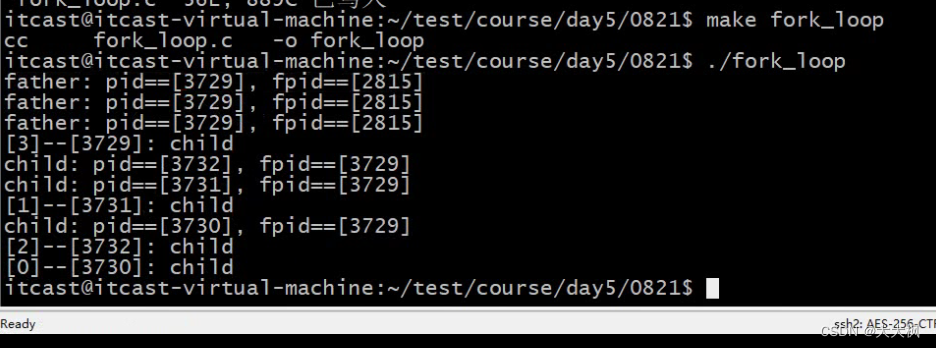
代码分析:循环创建N个子进程——为什么最后一个属于父进程?
黑马C/C 2018年32期代码分析 //循环创建n个子进程 #include <stdio.h> #include <stdlib.h> #include <string.h> #include <sys/types.h> #include <unistd.h>int main() {int i 0;for(i0; i<3; i){//创建子进程pid_t pid fork();if(pid&…...

【SpringBoot面试题整理-超级有效】
文章目录 1.SpringBoot如何解决跨域问题?2.为什么要用Spring Boot?3. Spring Boot的约定优于配置,你的理解是什么?4. SpringBoot有哪些优点?5. Spring Boot中自动装配机制的原理?6.SpringBoot支持哪些日志框…...

岩土工程仪器多通道振弦传感器信号转换器应用于隧道安全监测
岩土工程仪器多通道振弦传感器信号转换器应用于隧道安全监测 多通道振弦传感器信号转换器VTI104_DIN 是轨道安装式振弦传感器信号转换器,可将振弦、温度传感器信号转换为 RS485 数字信号和模拟信号输出,方便的接入已有监测系统。 传感器状态 专用指示灯方…...

西瓜书读书笔记整理(五)—— 第四章 决策树
第四章 决策树 4.1 基本流程4.1.1 什么是决策树算法4.1.2 决策树学习的目的4.1.3 决策树学习基本过程4.1.4 决策树学习基本算法4.1.5 递归结束的三种情况 4.2 划分选择4.2.1 信息增益(information gain)—— ID3 决策树学习算法属性划分准则4.2.2 信息增…...
STM32 4G学习
硬件连接 ATK-IDM750C模块可直接与正点原子 MiniSTM32F103开发板板载的ATK模块接口(ATK-MODULE)进行连接。 功能说明 ATK-IDM750C是正点原子(ALIENTEK)团队开发的一款高性能4G Cat1 DTU产品,支持移动4G、联通4G和…...

Golang 中实现实时聊天通讯
客户端代码 package mainimport ("fmt""log""net/url""os""os/signal""time""github.com/gorilla/websocket" )func main() {interrupt : make(chan os.Signal, 1)signal.Notify(interrupt, os.Interr…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

WEB3全栈开发——面试专业技能点P7前端与链上集成
一、Next.js技术栈 ✅ 概念介绍 Next.js 是一个基于 React 的 服务端渲染(SSR)与静态网站生成(SSG) 框架,由 Vercel 开发。它简化了构建生产级 React 应用的过程,并内置了很多特性: ✅ 文件系…...

[USACO23FEB] Bakery S
题目描述 Bessie 开了一家面包店! 在她的面包店里,Bessie 有一个烤箱,可以在 t C t_C tC 的时间内生产一块饼干或在 t M t_M tM 单位时间内生产一块松糕。 ( 1 ≤ t C , t M ≤ 10 9 ) (1 \le t_C,t_M \le 10^9) (1≤tC,tM≤109)。由于空间…...

《Offer来了:Java面试核心知识点精讲》大纲
文章目录 一、《Offer来了:Java面试核心知识点精讲》的典型大纲框架Java基础并发编程JVM原理数据库与缓存分布式架构系统设计二、《Offer来了:Java面试核心知识点精讲(原理篇)》技术文章大纲核心主题:Java基础原理与面试高频考点Java虚拟机(JVM)原理Java并发编程原理Jav…...
