浙大数据结构第七周之07-图4 哈利·波特的考试
基础知识:(最短路的前提都是在图中两条边之间的权值非定值)
(一)Dijkstra方法
算法实现:
dist[v]:表示从起点s到当前点v最短路径的长度
path[w]:表示到w顶点的上一个父顶点
(1)假设用带权的邻接矩阵G表示有向图,先初始化该邻接矩阵,其中与起点s之间有边的顶点i的G[s][i]初始化为权值,无边初始化为最初设定好的最大值INFINITY,path先全部初始化为-1
(2)将起点s加入集合S(S表示存放已找到最短路径的顶点)后,在T(T = V(V表示全体顶点)- S)里找与s之间距离最小的顶点v,将其加入S,标准是该顶点之前没有访问过(用一个作为全局变量的数组collect来记录是否访问过)且在集合T中与起点s之间加权距离最短
(3)加入v后,遍历整个图,寻找v的邻接点,如果w是v的邻接点且没有加入集合S,判断是否要修改dist[w],修改的标准是将原先从起点s不经过v到w的路径长度与从s经过v到w的路径长度比较,如果从s经过v到w的路径长度更小,就要更新dist[w],同时也要更新path[w]为v
c语言代码实现
/* 邻接矩阵存储 - 有权图的单源最短路算法 */Vertex FindMinDist( MGraph Graph, int dist[], int collected[] )
{ /* 返回未被收录顶点中dist最小者 */Vertex MinV, V;int MinDist = INFINITY;for (V=0; V<Graph->Nv; V++) {if ( collected[V]==false && dist[V]<MinDist) {/* 若V未被收录,且dist[V]更小 */MinDist = dist[V]; /* 更新最小距离 */MinV = V; /* 更新对应顶点 */}}if (MinDist < INFINITY) /* 若找到最小dist */return MinV; /* 返回对应的顶点下标 */else return ERROR; /* 若这样的顶点不存在,返回错误标记 */
}bool Dijkstra( MGraph Graph, int dist[], int path[], Vertex S )
{int collected[MaxVertexNum];Vertex V, W;/* 初始化:此处默认邻接矩阵中不存在的边用INFINITY表示 */for ( V=0; V<Graph->Nv; V++ ) {dist[V] = Graph->G[S][V];if ( dist[V]<INFINITY )path[V] = S;elsepath[V] = -1;collected[V] = false;}/* 先将起点收入集合 */dist[S] = 0;collected[S] = true;while (1) {/* V = 未被收录顶点中dist最小者 */V = FindMinDist( Graph, dist, collected );if ( V==ERROR ) /* 若这样的V不存在 */break; /* 算法结束 */collected[V] = true; /* 收录V */for( W=0; W<Graph->Nv; W++ ) /* 对图中的每个顶点W *//* 若W是V的邻接点并且未被收录 */if ( collected[W]==false && Graph->G[V][W]<INFINITY ) {if ( Graph->G[V][W]<0 ) /* 若有负边 */return false; /* 不能正确解决,返回错误标记 *//* 若收录V使得dist[W]变小 */if ( dist[V]+Graph->G[V][W] < dist[W] ) {dist[W] = dist[V]+Graph->G[V][W]; /* 更新dist[W] */path[W] = V; /* 更新S到W的路径 */}}} /* while结束*/return true; /* 算法执行完毕,返回正确标记 */
}二)Floyd算法:针对每一对顶点之间最短路径
Floyd算法怎么说呢,有点只可意会不可言传(可能我还没理解透),这篇文章写得挺好的
我的理解是最外层循环是中转点,中间一层循环是起点,最里面一层循环是终点,每次不断比较从起点不经过中转点到终点与从起点经过中转点到终点的路径,取最小值,并更改path对应的父顶点
/* 邻接矩阵存储 - 多源最短路算法 */bool Floyd( MGraph Graph, WeightType D[][MaxVertexNum], Vertex path[][MaxVertexNum] )
{Vertex i, j, k;/* 初始化 */for ( i=0; i<Graph->Nv; i++ )for( j=0; j<Graph->Nv; j++ ) {D[i][j] = Graph->G[i][j];path[i][j] = -1;}for( k=0; k<Graph->Nv; k++ )(中转点)for( i=0; i<Graph->Nv; i++ )(起点)for( j=0; j<Graph->Nv; j++ )(终点)if( D[i][k] + D[k][j] < D[i][j] ) {D[i][j] = D[i][k] + D[k][j];if ( i==j && D[i][j]<0 ) /* 若发现负值圈 */return false; /* 不能正确解决,返回错误标记 */path[i][j] = k;}return true; /* 算法执行完毕,返回正确标记 */
}Floyd算法好写(死记硬背)doge~但理解还是有点难度)
题目详情:
哈利·波特要考试了,他需要你的帮助。这门课学的是用魔咒将一种动物变成另一种动物的本事。例如将猫变成老鼠的魔咒是haha,将老鼠变成鱼的魔咒是hehe等等。反方向变化的魔咒就是简单地将原来的魔咒倒过来念,例如ahah可以将老鼠变成猫。另外,如果想把猫变成鱼,可以通过念一个直接魔咒lalala,也可以将猫变老鼠、老鼠变鱼的魔咒连起来念:hahahehe。
现在哈利·波特的手里有一本教材,里面列出了所有的变形魔咒和能变的动物。老师允许他自己带一只动物去考场,要考察他把这只动物变成任意一只指定动物的本事。于是他来问你:带什么动物去可以让最难变的那种动物(即该动物变为哈利·波特自己带去的动物所需要的魔咒最长)需要的魔咒最短?例如:如果只有猫、鼠、鱼,则显然哈利·波特应该带鼠去,因为鼠变成另外两种动物都只需要念4个字符;而如果带猫去,则至少需要念6个字符才能把猫变成鱼;同理,带鱼去也不是最好的选择。
输入格式:
输入说明:输入第1行给出两个正整数N (≤100)和M,其中N是考试涉及的动物总数,M是用于直接变形的魔咒条数。为简单起见,我们将动物按1~N编号。随后M行,每行给出了3个正整数,分别是两种动物的编号、以及它们之间变形需要的魔咒的长度(≤100),数字之间用空格分隔。
输出格式:
输出哈利·波特应该带去考场的动物的编号、以及最长的变形魔咒的长度,中间以空格分隔。如果只带1只动物是不可能完成所有变形要求的,则输出0。如果有若干只动物都可以备选,则输出编号最小的那只。
输入样例:
6 11
3 4 70
1 2 1
5 4 50
2 6 50
5 6 60
1 3 70
4 6 60
3 6 80
5 1 100
2 4 60
5 2 80
输出样例:
4 70主要思路:
题目要求找出任意两顶点之间最短路径,所以用Floyd算法
首先代码整体分为两部分:(1)读入图 (2)寻找动物
读入图就是前面常规
寻找动物是首先用Floyd求出任意两顶点之间最短路径,然后以各顶点为起点求出到其他顶点距离最大值,再在这些最大值里挑一个最小值,即是所要带的动物
第一次写错误:
(1)注意动物是从1开始标号的,所以在处理下标时要分两种情况,初始化的范围是从[0,vertexnums], 实际操作是[1, vertexnums]
(2)判断动物时如果找到的最大值就是默认的INFINITY,说明这个图里面存在不止一个连通集,输出0
代码实现:
#include <stdio.h>
#include <stdlib.h>
#define MAX_NODE_NUMS 105
#define FALSE 0
#define TRUE 1
#define NONE -1
#define INFINITY 1000
typedef int bool;
typedef struct MatrixGraphNode MatrixGraphNode;
typedef MatrixGraphNode* MGraph;
struct MatrixGraphNode {int VertexNums, EdgeNums;int Weight[MAX_NODE_NUMS][MAX_NODE_NUMS];
};
MGraph CreateEmptyGraph(int vertexNums, int edgeNums) {MGraph graph = (MGraph)malloc(sizeof(MatrixGraphNode));graph->VertexNums = vertexNums;graph->EdgeNums = edgeNums;for(int i = 0; i <= vertexNums; i++) {for(int j = 0; j <= vertexNums; j++) {graph->Weight[i][j] = NONE;}}return graph;
}
void InsertEdge(int start, int end, int weight, MGraph graph) {graph->Weight[start][end] = weight;graph->Weight[end][start] = weight;return;
}
MGraph BuildGraph(int vertexNums, int edgeNums) {MGraph graph = CreateEmptyGraph(vertexNums, edgeNums);for(int i = 0; i < edgeNums; i++) {int start, end, weight;scanf("%d %d %d", &start, &end, &weight);InsertEdge(start, end, weight, graph);}return graph;
}
void Floyd(int dis[][MAX_NODE_NUMS], MGraph graph) {for(int i = 1; i <= graph->VertexNums; i++) {for(int j = 1; j <= graph->VertexNums; j++) {if(i == j) {dis[i][j] = FALSE;}else if(graph->Weight[i][j] != NONE){dis[i][j] = graph->Weight[i][j];}else if(graph->Weight[i][j] == NONE) {dis[i][j] = INFINITY;}}}for(int i = 1; i <= graph->VertexNums; i++) {for(int j = 1; j <= graph->VertexNums; j++) {for(int k = 1; k <= graph->VertexNums; k++) {if(dis[j][k] > dis[j][i] + dis[i][k]) {dis[j][k] = dis[j][i] + dis[i][k];}}}}
}
int FindLongestDistance(int dis[][MAX_NODE_NUMS], int start, int vertexNums) {int ret = FALSE;for(int i = 1; i <= vertexNums; i++) {if(i != start && dis[start][i] > ret) {ret = dis[start][i];}}return ret;
}
void FindAnimal(MGraph graph) {int dis[MAX_NODE_NUMS][MAX_NODE_NUMS];Floyd(dis, graph);int animal = FALSE;int longestDistance = FALSE;int minInLongestDistance = INFINITY;for(int i = 1; i <= graph->VertexNums; i++) {longestDistance = FindLongestDistance(dis, i, graph->VertexNums);if(longestDistance == INFINITY) {printf("%d", FALSE);return;}else {if(longestDistance < minInLongestDistance) {animal = i;minInLongestDistance = longestDistance;}}}printf("%d %d", animal, minInLongestDistance);return;
}
int main() {int vertexNums, edgeNums;scanf("%d %d", &vertexNums, &edgeNums);MGraph graph = BuildGraph(vertexNums, edgeNums);FindAnimal(graph);free(graph);return 0;
}相关文章:

浙大数据结构第七周之07-图4 哈利·波特的考试
基础知识:(最短路的前提都是在图中两条边之间的权值非定值) (一)Dijkstra方法 算法实现: …...
vue2-vue项目中你是如何解决跨域的?
1、跨域是什么? 跨域本质是浏览器基于同源策略的一种安全手段。 同源策略(sameoriginpolicy),是一种约定,它是浏览器最核心也是最基本的安全功能。 所谓同源(即指在同一个域)具有以下三个相同点…...

【Paper Reading】DETR:End-to-End Object Detection with Transformers
背景 Transformer已经在NLP领域大展拳脚,逐步替代了LSTM/GRU等相关的Recurrent Neural Networks,相比于传统的RNN,Transformer主要具有以下几点优势 可解决长时序依赖问题,因为Transformer在计算attention的时候是在全局维度进行…...

【rust/入门】windows安装rust gnu环境(折腾)
说在前面 首先说明,我是rust入门选手,之前都是在wsl写rust,突然想在windows下装下rust。windows版本:windows11 22H2原文换源 心路历程 看到教程我陷入了沉默,(官方推荐) 打开Microsoft C Build Tools我开始不解&…...

java面试---字符串相关内容
字符串 1. 什么是Java中的字符串池(String Pool)?2. String、StringBuilder和StringBuffer之间的区别是什么?3. 如何比较两个字符串的内容是否相等?4、equals和的区别5. String类有哪些常用的方法? 1. 什么…...
MYSQL进阶-事务的基础知识
1.什么是数据库事务? 就是把好几个sql语句打包成一个整体执行,要么全部成功,要么全部失败!!! 事务是一个不可分割的数据库操作序列,也是数据库并发控制的基本单位,其执 行的结果必…...
【C++】C++面向对象,泛型编程总结篇(封装,继承,多态,模板)|(秋招篇)
文章目录 前言如何理解面向对象?如何理解泛型编程?C面向对象的三大特性是什么构造函数有哪几种?讲一下移动构造函数当我们定义一个类 系统会自动帮我们生成哪些函数?标题讲一下类中三类成员(公有私有保护)三…...
【Github】作为程序员不得不知道的几款Github加速神器
文章目录 背景推荐1:FastGithub推荐2:dev-sidecar推荐3:Watt Toolkit推荐4:篡改猴插件用户脚本1)下载安装-->篡改猴 Tampermonkey 插件2)下载安装-->Github 增强 - 高速下载 用户脚本 推荐5ÿ…...

react18之08自定义hook (简单的axios-get、修改浏览器title、localStorage、获取滚动条位置、img转换为base64)
目录 react18之自定义hook ()01:自定义一个 简单的axios hook 发起get请求useHttp.jsx使用useHttp hook效果 02:自定义一个 修改浏览器title hook03:自定义一个 localStorage(获取、存储、移除) hookuseLocalStorage.jsx使用hook效果 04&…...

对CommonJS、AMD、CMD、ES Module的理解
CommonJS 常用于:服务器端,node,webpack 特点:同步/运行时加载,磁盘读取速度快 语法: // 1. 导出:通过module.exports或exports来暴露模块 module.exports { attr1, attr2 } ex…...
)
JVM之类加载与字节码(二)
3. 编译期处理 什么是语法糖 所谓的 语法糖 ,其实就是指 java 编译器把 *.java 源码编译为 *.class 字节码的过程中,自动生成 和转换的一些代码,主要是为了减轻程序员的负担,算是 java 编译器给我们的一个额外福利(给…...
安装linux操作系统
安装虚拟机的步骤: 安装linux系统 之后开启虚拟机 之后重启,打开虚拟机,登录root账号...
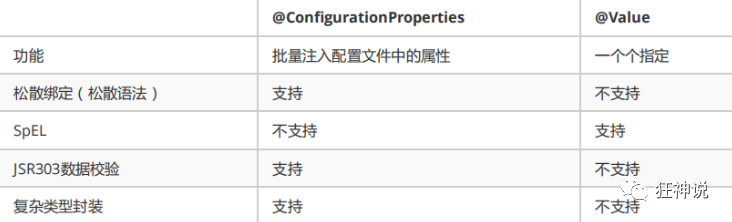
【SpringBoot】知识
.第一个程序HelloWorld 项目创建方式:使用 IDEA 直接创建项目 1、创建一个新项目 2、选择spring initalizr , 可以看到默认就是去官网的快速构建工具那里实现 3、填写项目信息 4、选择初始化的组件(初学勾选 Web 即可) 5、填…...
react ant add/change created_at
1.引入ant的 Table import { Table, Space, Button, message } from antd; 2.获得接口的数据的时候增加上创建时间 const response await axios.get(${Config.BASE_URL}/api/v1/calculation_plans?token${getToken()});if (response.data.message ok) {const data respon…...
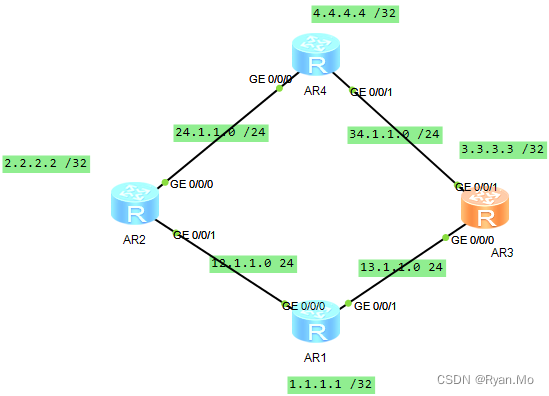
OSPF 动态路由协议 路由传递
影响OSPF路由选择的因素: 1.OSPF路由的开销值:宽带参考值默认为100. COST1000/接口带宽。此时接口 带宽的值可更改,更改后只改变参考数值,带宽仍然为初始值。 注意:更改COST需要 在路由的入方向,数据的出方…...

5.kubeadm安装
文章目录 kubeadm部署环境初始化所有的节点安装Docker所有节点安装kubeadm,kubelet和kubectl初始化方法一,配置文件初始化方法二,命令初始化 网络插件node节点总结 证书过期方法一方法二总结 部署Dashboard kubeadm部署 环境初始化 ###所有…...

【雕爷学编程】Arduino动手做(180)---Seeeduino Lotus开发板2
37款传感器与执行器的提法,在网络上广泛流传,其实Arduino能够兼容的传感器模块肯定是不止这37种的。鉴于本人手头积累了一些传感器和执行器模块,依照实践出真知(一定要动手做)的理念,以学习和交流为目的&am…...

6.5 池化层
是什么:池化层跟卷积层类似有个滑动窗口,用来取一个区域内的最大值或者平均值。 作用:卷积神经网络的最后的部分应该要看到整个图像的全局,通过池化(汇聚)操作,逐渐汇聚要取的像素,最终实现学习全局表示的…...
etcd
文章目录 etcd单机安装设置键值对watch操作读取键过往版本的值压缩修订版本lease租约(过期机制)授予租约撤销租约keepAlive续约获取租约信息 事务基于etcd实现分布式锁原生实现官方 concurrency 包实现 服务注册与发现Go 操作 Etcd 参考 etcd etcd 是一…...
W5500-EVB-PICO做DNS Client进行域名解析(四)
前言 在上一章节中我们用W5500-EVB-PICO通过dhcp获取ip地址(网关,子网掩码,dns服务器)等信息,给我们的开发板配置网络信息,成功的接入网络中,那么本章将教大家如何让我们的开发板进行DNS域名解析…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

相关类相关的可视化图像总结
目录 一、散点图 二、气泡图 三、相关图 四、热力图 五、二维密度图 六、多模态二维密度图 七、雷达图 八、桑基图 九、总结 一、散点图 特点 通过点的位置展示两个连续变量之间的关系,可直观判断线性相关、非线性相关或无相关关系,点的分布密…...

Java后端检查空条件查询
通过抛出运行异常:throw new RuntimeException("请输入查询条件!");BranchWarehouseServiceImpl.java // 查询试剂交易(入库/出库)记录Overridepublic List<BranchWarehouseTransactions> queryForReagent(Branch…...
