当前位置： 首页 > news >正文

Typescript中的元组与数组的区别

news 2026/2/9 5:33:52

Typescript中的元组与数组的区别

元组可以应用在经纬度这样明确固定长度和类型的场景下

//元组和数组类似，但是类型注解时会不一样//元组赋值的类型、位置、个数需要和定义的类型、位置、个数完全一致，不然会报错。 // 数组 某个位置的值可以是注解中的任何一个,且个数没有限制
const arr: (string | number)[] = ["aaa", 111, "bbb"];// 元组 每一项数据类型、数量、位置，必须一致
const arr2: [string, string, number] = ["aaa", "bbb", 111];

如果类型不一致会报错，如下图所示
在这里插入图片描述

如果数量不一致也会报错，如下图所示在这里插入图片描述
如果位置不一致也会报错，如下图所示
在这里插入图片描述

相关文章：

Typescript中的元组与数组的区别

Typescript中的元组与数组的区别 元组可以应用在经纬度这样明确固定长度和类型的场景下 //元组和数组类似，但是类型注解时会不一样//元组赋值的类型、位置、个数需要和定义的类型、位置、个数完全一致，不然会报错。 // 数组 某个位置的值可以是注解中的…...

编程日记 2023/8/7 12:05:20

SpringBoot的index首页的访问、自定义Favicon图标

目录 1. index首页1.1 index首页访问规则的源码1.2 index首页的访问 2. 自定义Favicon图标 1. index首页 1.1 index首页访问规则的源码 package org.springframework.boot.autoconfigure.web.servlet; ......省略部分......// SpringBoot给容器中放WebMvcConfigurationSuppor…...

编程日记 2023/8/7 12:04:19

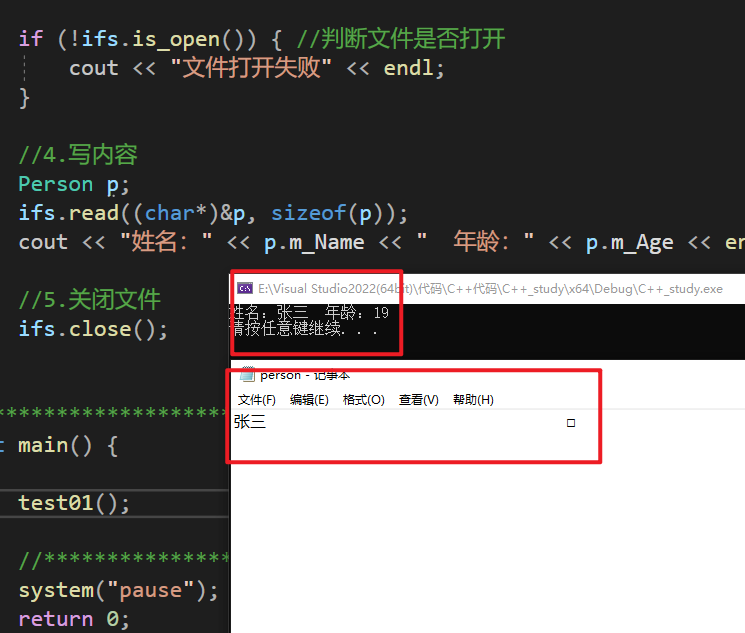
【C++】C++文件操作-文本文件/二进制文件

0.前言 一、文本文件 1.写文件 代码 #include <iostream> using namespace std; #include <fstream> //头文件包含//************************************** //文本文件 写文件 void test01() {//1.包含文件 fstream//2.创建流对象ofstream ofs;//3.指导打开方式…...

编程日记 2023/8/7 12:03:18

java通过http网络url下载文件

Testpublic void test3() throws ParseException {String fileUrl "http://*****/123.pdf";String savePath "C:\\Users\\HHH\\Desktop\\文件\\123.pdf";try {URL url new URL(fileUrl);InputStream inputStream url.openStream();Path outputPath Pa…...

编程日记 2023/8/7 12:02:17

网络安全【黑客】自学

1.什么是网络安全&#xff1f; 网络安全可以基于攻击和防御视角来分类&#xff0c;我们经常听到的 “红队”、“渗透测试” 等就是研究攻击技术&#xff0c;而“蓝队”、“安全运营”、“安全运维”则研究防御技术。 无论网络、Web、移动、桌面、云等哪个领域&#xff0c;都有…...

编程日记 2023/8/7 12:01:14

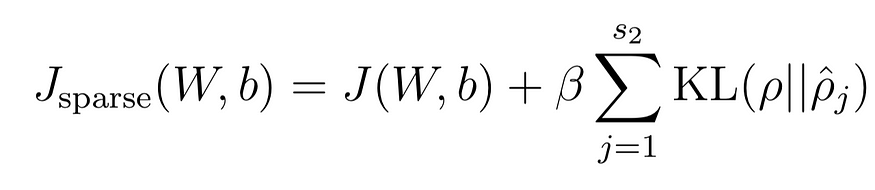
PCA和自动编码器：每个人都能理解的算法

一、说明 本文的主要重点是提供主成分分析 &#xff08;PCA&#xff09; 和自动编码器数据转换技术的直观信息。我不打算深入研究支撑这些模型的数学理论&#xff0c;因为已经有大量的资源可用。 二、pca降维和自编码 2.1 pca和自编码的共同点 自动编码器通过组合数据最重要的特…...

编程日记 2023/8/7 12:00:13

C++——STL容器【priority_queue】模拟实现

本章代码&#xff1a;优先级队列模拟实现、priority_queue文档 文章目录 &#x1f408;1. priority_queue介绍&#x1f984;2. priority_queue模拟实现&#x1f427;2.1 构造函数&#x1f427;2.2 建堆向下调整向上调整 &#x1f427;2.3 仿函数&#x1f427;2.4 push & po…...

编程日记 2023/8/7 11:59:12

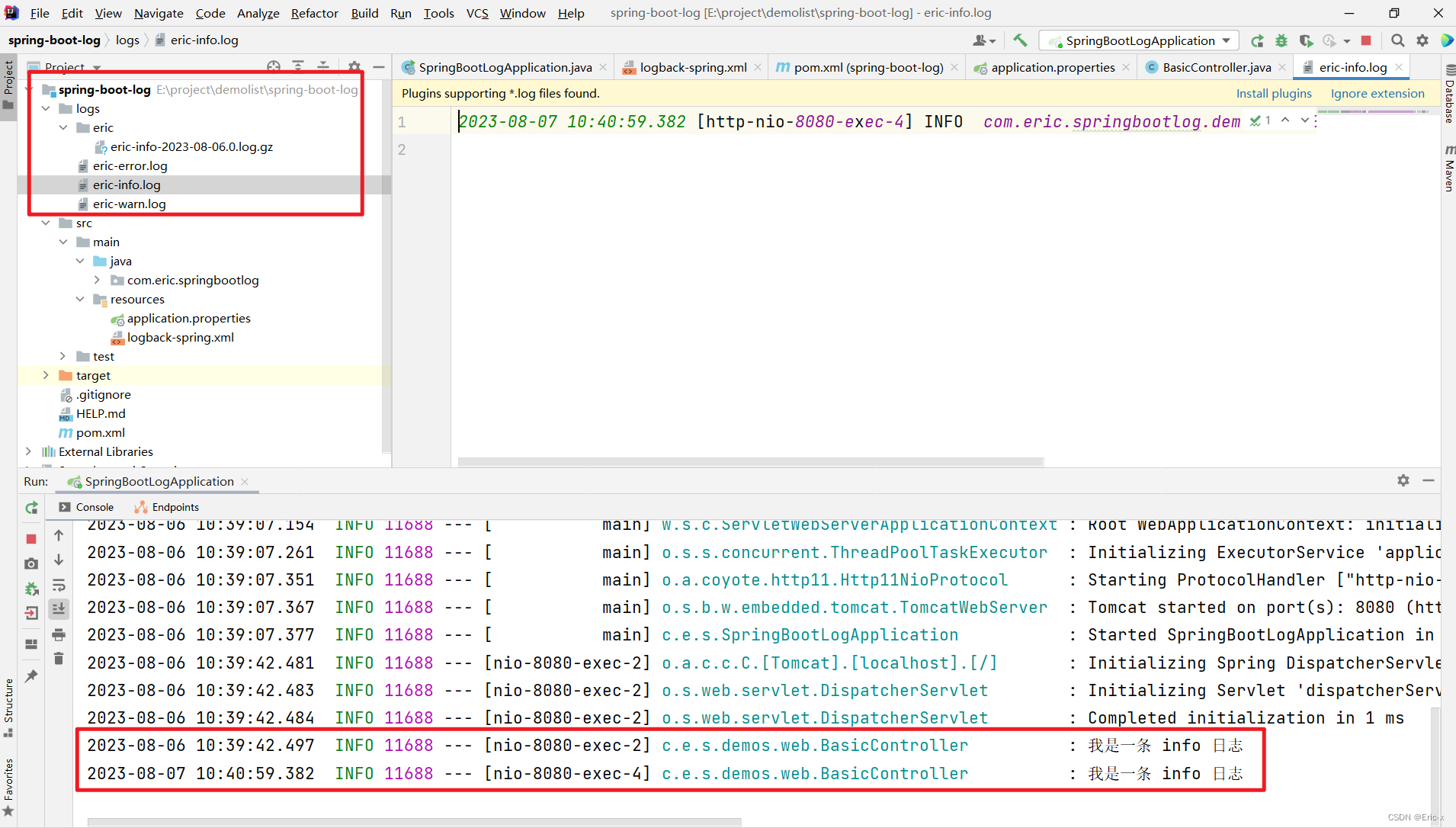
SpringBoot实现文件记录日志，日志文件自动归档和压缩

&#x1f60a; 作者&#xff1a; Eric &#x1f496; 主页&#xff1a; https://blog.csdn.net/weixin_47316183?typeblog &#x1f389; 主题&#xff1a;SpringBoot实现文件记录日志&#xff0c;日志文件自动归档和压缩 ⏱️ 创作时间&#xff1a; 2023年08月06日 文章目…...

编程日记 2023/8/7 11:58:09

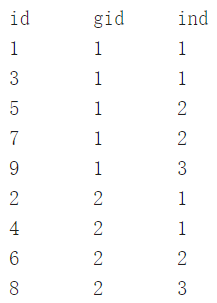
MySQL 窗口函数

聚合函数作为窗口函数 设聚合函数为op语法结构&#xff1a; op(字段名A) over(partition by 字段名B order by 字段名C rows between D1 and D2) 其中&#xff1a; partition by&#xff1a;按照某一字段将数据进行分组 order by&#xff1a;按照某一字段将数据进行排序&…...

编程日记 2023/8/7 11:57:07

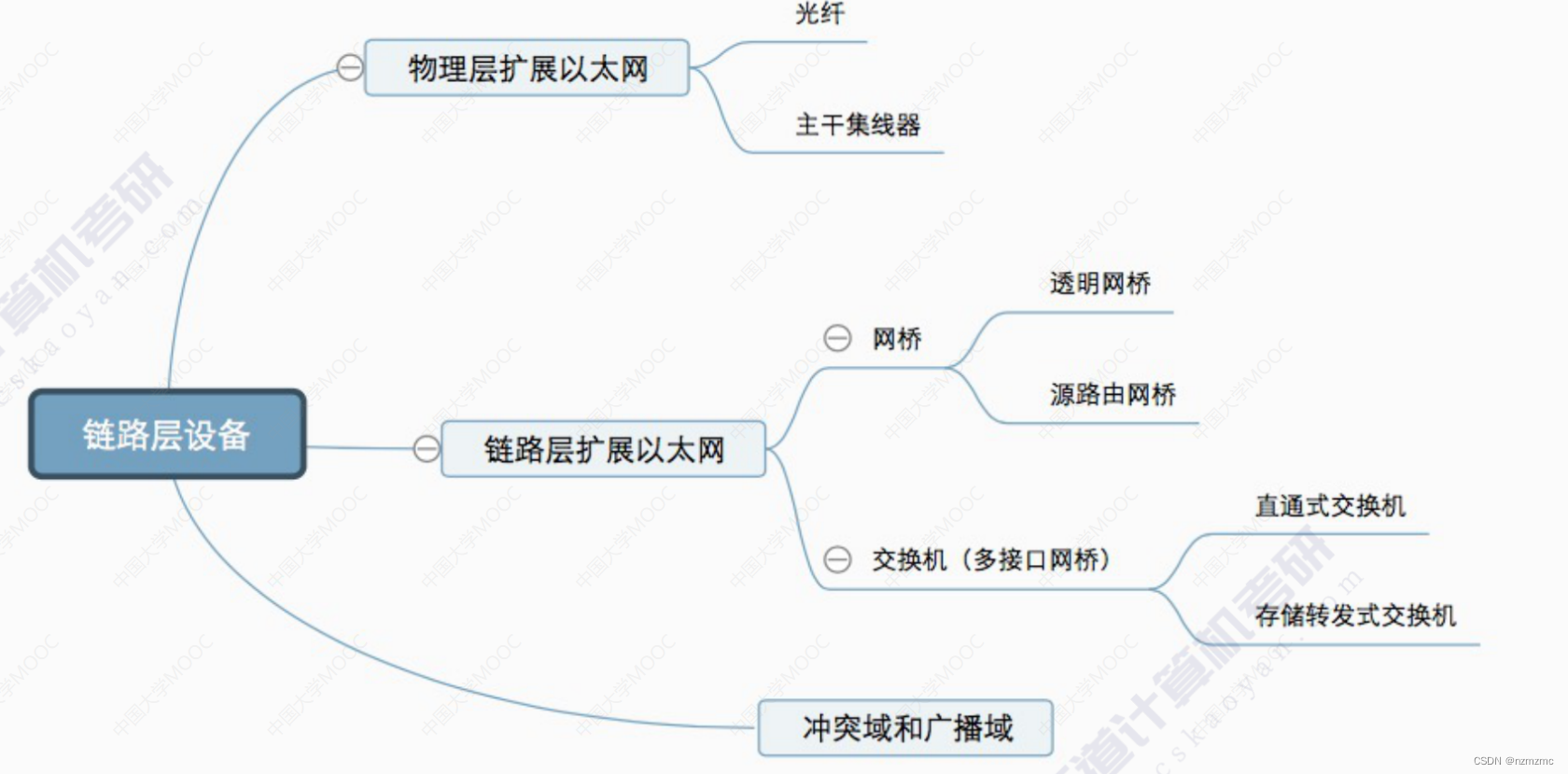
0140 数据链路层2

目录 3.数据链路层 3.6局域网 3.7广域网 3.8数据链路层设备 部分习题 3.数据链路层 3.6局域网 3.7广域网 3.8数据链路层设备 部分习题 1.如果使用5类UTP来设计一个覆盖范围为200m的10BASE-T以太网&#xff0c;需要采用的设备是&#xff08;&#xff09; A.放大器 …...

编程日记 2023/8/7 11:56:06

Python字典的应用场景

Python字典是一种无序、可变的数据类型&#xff0c;它由键值对组成。字典在Python中被广泛应用&#xff0c;以下是一些常见的应用场景&#xff1a; 数据存储和检索&#xff1a;字典可以用来存储和检索大量的数据&#xff0c;通过使用键来快速访问对应的值。例如&#xff0c;可以…...

编程日记 2023/8/7 11:55:06

关于外贸跟进客户过程中需要注意的地方

如果你感觉业务进展困难&#xff0c;多去看一些书&#xff0c;多去链接一些人&#xff0c;特别是优秀的人&#xff0c;多交流会让你思维更加开阔&#xff0c;笔记做好实践起来&#xff0c;就会有收获&#xff01; 我记得汪老师说过&#xff1a;跟进客户&#xff0c;当你准备好…...

编程日记 2023/8/7 11:54:04

AI绘画：两组赛博咒语和ComfyUI使用方法

虽迟但到啊&#xff0c;上次说过要发&#xff0c;必然是要发滴&#xff01; 本来我是可以直接发的&#xff0c;但是我又想着发关键词的同时&#xff0c;最好是讲解一下用法&#xff0c;这样更友好。所以就拖了一天&#xff01; 下面先展示一下两套咒语的效果&#xff1a; 这套…...

编程日记 2023/8/7 11:53:03

Nacos源码 (2) 核心模块

返回目录 整体架构 服务管理&#xff1a;实现服务CRUD&#xff0c;域名CRUD&#xff0c;服务健康状态检查&#xff0c;服务权重管理等功能配置管理&#xff1a;实现配置管CRUD&#xff0c;版本管理&#xff0c;灰度管理&#xff0c;监听管理&#xff0c;推送轨迹&#xff0c;聚…...

编程日记 2023/8/7 11:52:01

MySQL之深入InnoDB存储引擎——Buffer Pool

文章目录 一、空闲链表的管理二、缓冲页的哈希处理三、Flush链表的管理四、LRU链表的管理五、脏页刷新六、多Buffer Pool实例 InnoDB存储引擎是基于磁盘存储的&#xff0c;并将其中的记录按照页的方式进行管理。在数据库系统中&#xff0c;由于CPU速度与磁盘速度之间的鸿沟&…...

编程日记 2023/8/7 11:51:00

网络安全（秋招）如何拿到offer?(含面试题）

以下为网络安全各个方向涉及的面试题&#xff0c;星数越多代表问题出现的几率越大&#xff0c;祝各位都能找到满意的工作。 注&#xff1a;本套面试题&#xff0c;已整理成pdf文档&#xff0c;但内容还在持续更新中&#xff0c;因为无论如何都不可能覆盖所有的面试问题&#xf…...

编程日记 2023/8/7 11:49:58

笙默考试管理系统-MyExamTest----classranking（2）

笙默考试管理系统-MyExamTest----classranking&#xff08;2&#xff09; 目录 笙默考试管理系统-MyExamTest----classranking&#xff08;2&#xff09; 一、 笙默考试管理系统-MyExamTest----classranking 二、 笙默考试管理系统-MyExamTest----classranking 三、 笙…...

编程日记 2023/8/7 11:48:57

基于python的一个元素多种定位方式

基于 Python 的 Page Factory 设计模式测试库, 类似于Java的Page Factory模式&#xff0c;旨在减少代码冗余&#xff0c;简单易用&#xff0c;具有高度的可扩展能力。 支持以annotation的方式定义元素 支持同一个元素多种定位方式 支持动态的定位方式 安装 pip install pyth…...

编程日记 2023/8/7 11:47:57

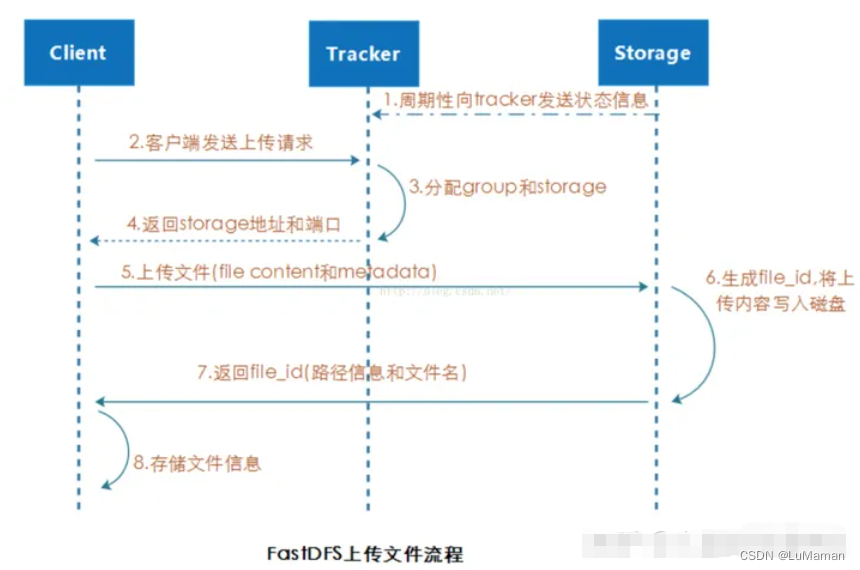
Fastdfs集群搭建

一、简单介绍&#xff1a; FastDFS是一个开源的高性能分布式文件系统&#xff08;DFS&#xff09;。 它的主要功能包括&#xff1a;文件存储&#xff0c;文件同步和文件访问&#xff0c;以及高容量和负载平衡。主要解决了海量数据存储问题&#xff0c;特别适合以中小文件&…...

编程日记 2023/8/7 11:46:55

【深度学习】Vision Transformer论文，ViT的一些见解《 一幅图像抵得上16x16个词：用于大规模图像识别的Transformer模型》

必看文章&#xff1a;https://blog.csdn.net/qq_37541097/article/details/118242600 论文名称&#xff1a; An Image Is Worth 16x16 Words: Transformers For Image Recognition At Scale 论文下载&#xff1a;https://arxiv.org/abs/2010.11929 官方代码&#xff1a;https:…...

编程日记 2023/8/7 11:45:53

stm32G473的flash模式是单bank还是双bank？

今天突然有人stm32G473的flash模式是单bank还是双bank&#xff1f;由于时间太久&#xff0c;我真忘记了。搜搜发现&#xff0c;还真有人和我一样。见下面的链接&#xff1a;https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

编程新知 2026/2/8 20:41:51

Unity3D中Gfx.WaitForPresent优化方案

前言 在Unity中&#xff0c;Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染&#xff08;即CPU被阻塞&#xff09;&#xff0c;这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案&#xff1a; 对惹&#xff0c;这里有一个游戏开发交流小组&…...

编程新知 2026/2/7 17:31:44

Appium+python自动化（十六）- ADB命令

简介 Android 调试桥(adb)是多种用途的工具&#xff0c;该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具&#xff0c;其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利&#xff0c;如安装和调试…...

编程新知 2026/1/21 18:20:51

SCAU期末笔记 - 数据分析与数据挖掘题库解析

这门怎么题库答案不全啊日 来简单学一下子来 一、选择题&#xff08;可多选&#xff09; 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘&#xff1a;专注于发现数据中…...

编程新知 2026/1/24 14:15:43

CMake基础：构建流程详解

目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

编程新知 2026/2/2 7:39:34

【算法训练营Day07】字符串part1

文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接&#xff1a;344. 反转字符串 双指针法&#xff0c;两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

编程新知 2025/8/27 14:38:58

Razor编程中@Html的方法使用大全

文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

编程新知 2026/1/28 4:50:33

解决：Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist

现象&#xff1a; android studio报错&#xff1a; [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决&#xff1a; 不要动CMakeLists.…...

编程新知 2025/12/15 0:46:42

深入理解Optional：处理空指针异常

1. 使用Optional处理可能为空的集合 在Java开发中&#xff0c;集合判空是一个常见但容易出错的场景。传统方式虽然可行&#xff0c;但存在一些潜在问题&#xff1a; // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

编程新知 2025/12/19 19:15:39

redis和redission的区别

Redis 和 Redisson 是两个密切相关但又本质不同的技术&#xff0c;它们扮演着完全不同的角色&#xff1a; Redis: 内存数据库/数据结构存储 本质&#xff1a; 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能&#xff1a; 提供丰…...

编程新知 2025/11/6 1:34:07