【数模】主成分分析PCA
- 主成分分析(Principal Component Analysis,PCA),是一种降维算法,它能将多个指标转换为少数几个主成分,这些主成分是原始变量的线性组合,且彼此之间互不相关,其能反映出原始数据的大部分信息。
- 使用场景:一般来说,当研究的问题涉及到多变量且变量之间存在很强的相关性时,可考虑使用主成分分析的方法来对数据进行简化。
一、主成分分析的简要介绍
1.1 降维
- 主成分分析:把原来多个变量划为少数几个综合指标的一种统计分析方法 → 降维
- 降维的优点:
- 使得数据集更易使用;
- 降低算法的计算开销;
- 去除噪声;
- 使得结果容易理解。
1.2 PCA详细证明过程
- 参考视频(需要基础:多元统计和线性代数)
二、PCA的计算步骤
假设有n个样本,p个指标,则可构成大小为n×p的样本矩阵x: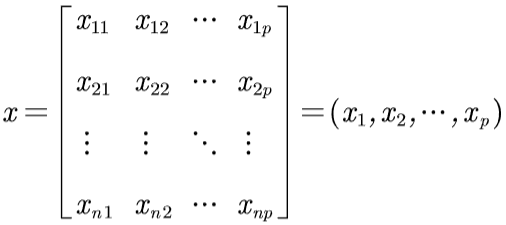
2.1 标准化处理

2.2 计算标准化样本的协方差矩阵
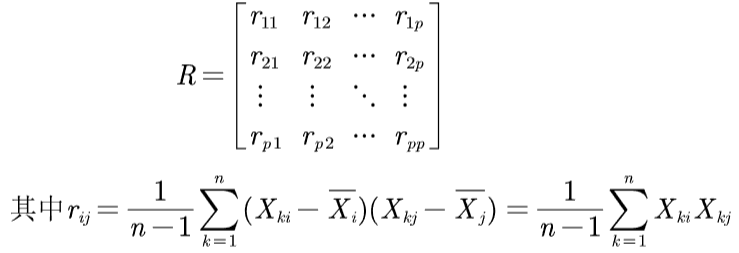
( 2.1和2.2合并:直接计算x矩阵的样本相关系数矩阵 )
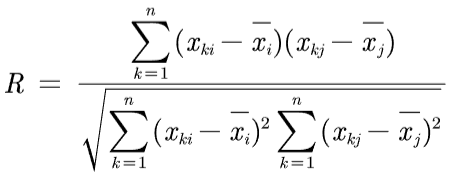
2.3 计算R的特征值和特征向量
- 软件会算好,不必自己算,Matlab中计算特征值和特征向量的函数:
eig(R)函数 - R一定是半正定矩阵 → 则一定非负(线代知识)

2.4 计算主成分贡献率以及累计贡献率

2.5 写出主成分
- 一般取累计贡献率超过80%的特征值所对应的第一、第二、… 、第m(m≤p)个主成分。第i个主成分:F=a1iX1+ a2iX2+…十apiXp(i=1,2,…,m)
2.6 根据系数(api)分析主成分代表的意义
- 对于某个主成分而言,指标前面的系数越大,代表该指标对于该主成分的影响越大
2.7 利用主成分的结果进行后续的分析
- 主成分得分:不能评价类模型!
- 主成分可用于聚类分析→方便画图
- 主成分可用于回归分析
三、主成分分析的应用例题1
3.1 题目
- 在制定服装标准的过程中,对128名成年男子的身材进行了测量,每人测得的指标中含有这样六项:身高(x1)、坐高(x2) 、胸围(x3) 、手臂长(x4) 、肋围(x5)和腰围(x6) 。所得样本相关系数矩阵(对称矩阵)列于下表。
- 注意:本题给我们的数据直接就是样本相关系数矩阵,一般建模时,得到的数据是最原始的数据(每一列是指标,每一行是样本)。
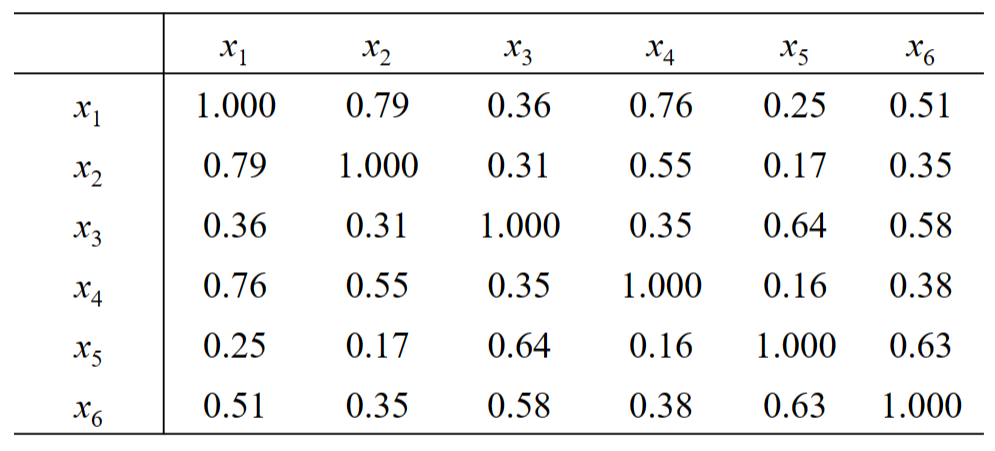
3.2 计算关键变量
- 经过计算,相关系数矩阵的特征值、相应的特征向量以及贡献率列于下表:
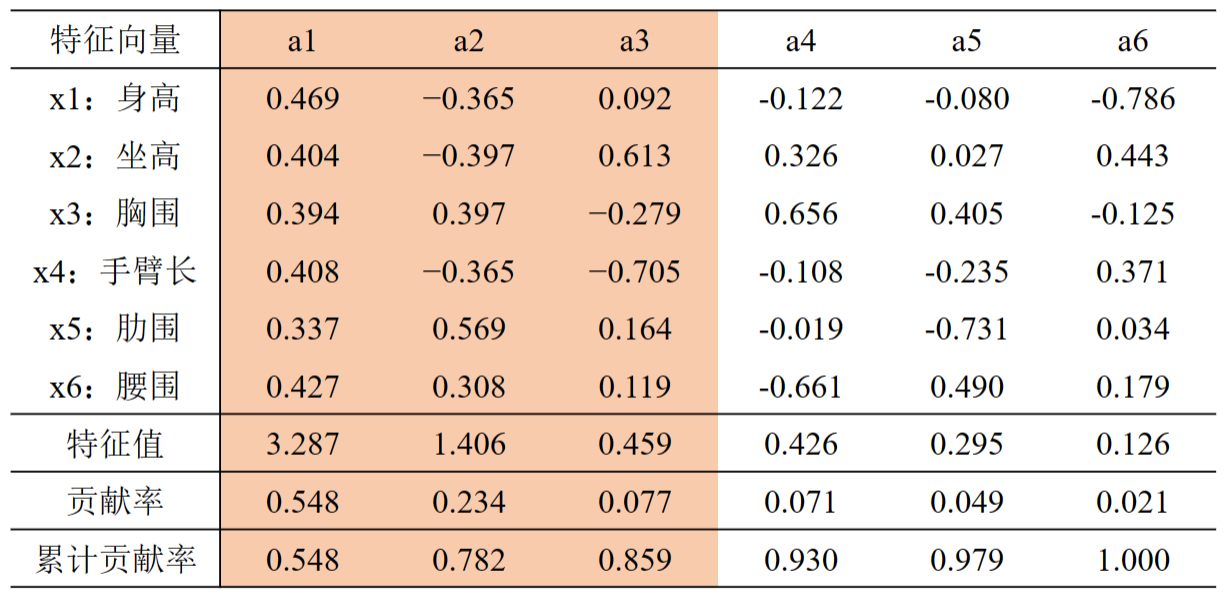
- 从表中可以看到前三个主成分的累计贡献率达85.9%,因此可以考虑只取前面三个主成分,它们能够很好地概括原始变量。
3.3 写出主成分并简要分析

- 第一主成分F1对所有(标准化)原始变量都有近似相等的正载荷,故称第一主成分为(身材)大小成分。
- 第二主成分F2在X3,X5,X6上有中等程度的正载荷,而在X1,X2,X4上有中等程度的负载荷,称第二主成分为形状成分(或胖瘦成分)。
- 第三主成分F3在X2上有大的正载荷,在X4上有大的负载荷,而在其余变量上的载荷都较小,可称第三主成分为臂长成分。
- 注:由于第三主成分的贡献率不高(7.65%)且实际意义也不太重要,因此我们也可以考虑只取前两个主成分进行分析。
3.4 主成分分析的说明
- 在主成分分析中,我们首先应保证所提取的前几个主成分的累计贡献率达到一个较高的水平,其次对这些被提取的主成分必须都能够给出符合实际背景和意义的解释。
- 主成分的解释其含义一般多少带有点模糊性,不像原始变量的含义那么清楚、确切,这是变量降维过程中不得不付出的代价。 因此,提取的主成分个数m通常应明显小于原始变量个数p(除非p本身较小),否则维数降低的“利”可能抵不过主成分含义不如原始变量清楚的“弊”。
- 如果原始变量之间具有较高的相关性,则前面少数几个主成分的累计贡献率通常就能达到一个较高水平,也就是说,此时的累计贡献率通常较易得到满足。
- 主成分分析的困难之处主要在于要能够给出主成分的较好解释,所提取的主成分中如有一个主成分解释不了,整个主成分分析也就失败了。
- 主成分分析是变量降维的一种重要、常用的方法,简单的说,该方法要应用得成功,一是靠原始变量的合理选取,二是靠“运气”。
——参考教材:《应用多元统计分析》王学民
四、主成分分析的应用例题2
4.1 题目
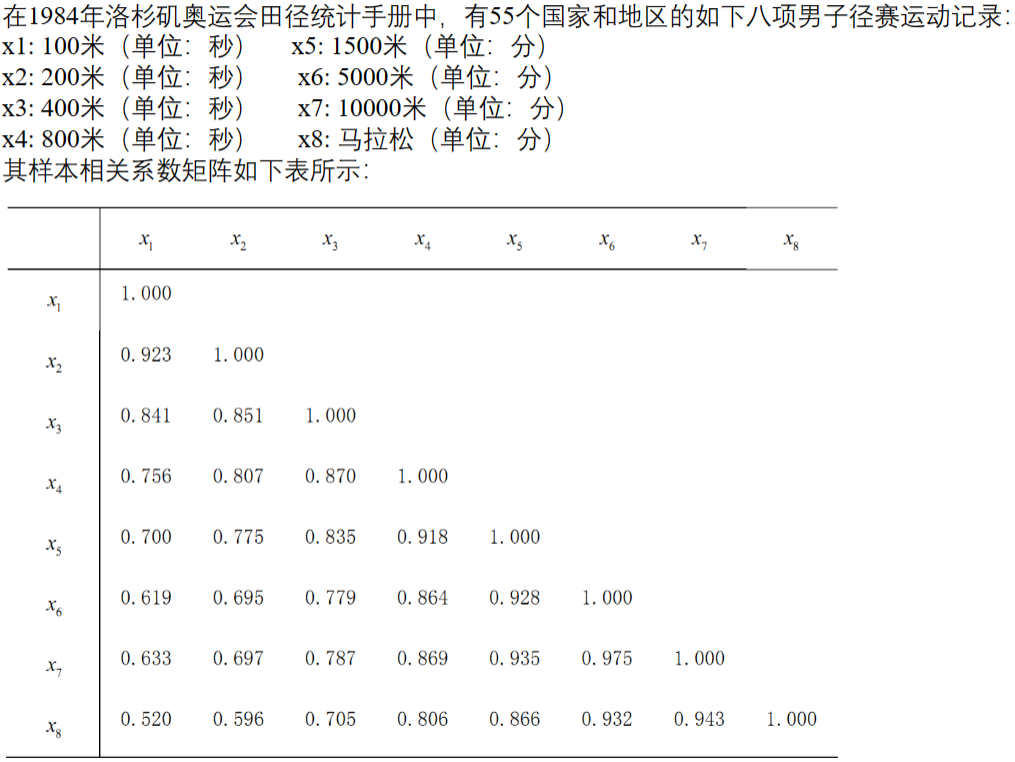
4.2 计算关键变量
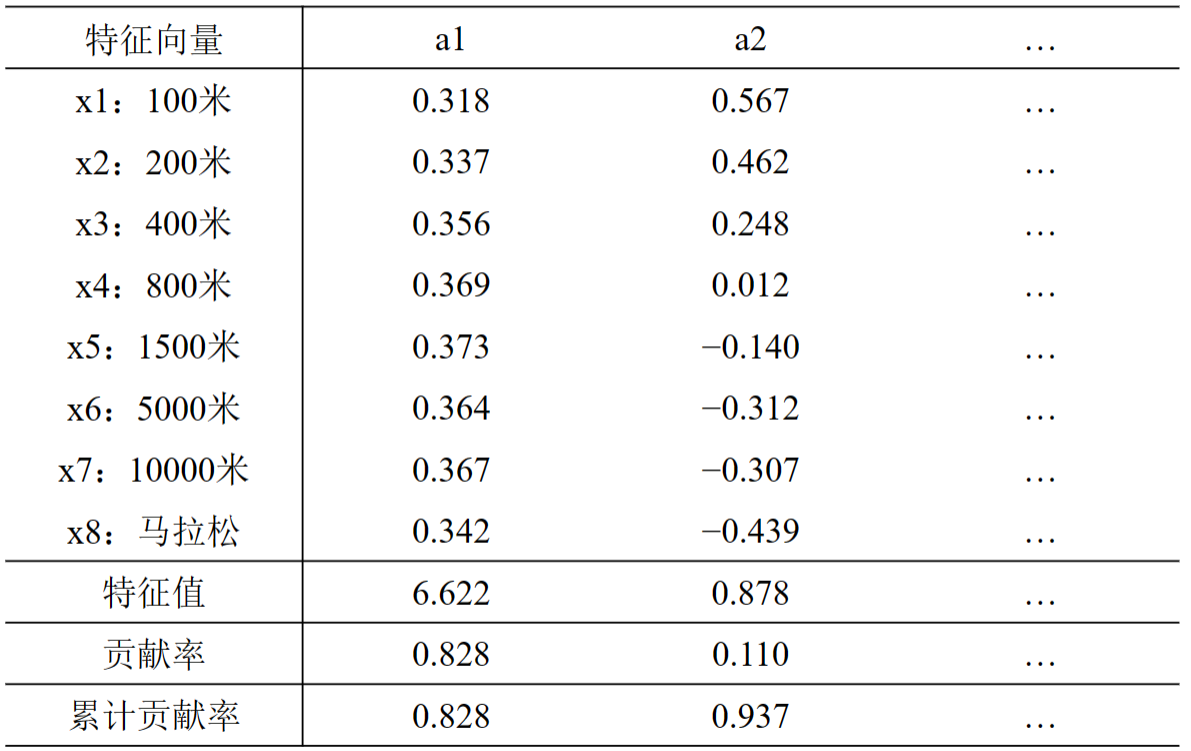
4.3 对主成分的简要分析
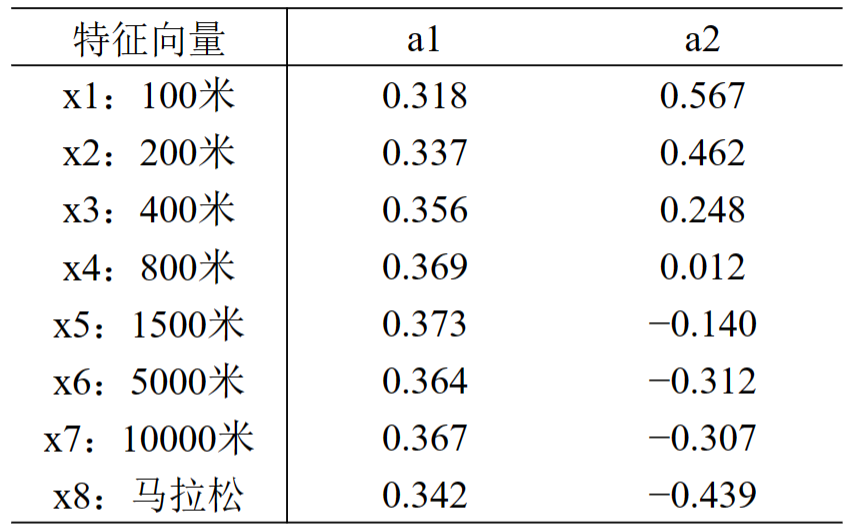
由上表可知,前两个主成分的累计贡献率已高达93.7%,第一主成分F1在所有变量上有几乎相等的正载荷,可称为在径赛项目上的强弱成分。第二主成分F2在各个指标上的载荷基本上逐个递减,反映了速度与耐力成绩的对比
4.4 Matlab代码
PCA.m(更加详细的代码注释可见源代码)
%% 第一步:对数据x标准化为X
X=zscore(x);%% 第二步:计算样本协方差矩阵
R = cov(X);
%% 注意:以上两步可合并为下面一步:直接计算样本相关系数矩阵
R = corrcoef(x);%% 第三步:计算R的特征值和特征向量
[V,D] = eig(R); % V 特征向量矩阵 D 特征值构成的对角矩阵%% 第四步:计算主成分贡献率和累计贡献率
lambda = diag(D); % diag函数用于得到一个矩阵的主对角线元素值(返回的是列向量)
lambda = lambda(end:-1:1); % 因为lambda向量是从小大到排序的,我们将其调个头
% 计算贡献率
contribution_rate = lambda / sum(lambda);
% 计算累计贡献率 cumsum是求累加值的函数
cum_contribution_rate = cumsum(lambda)/ sum(lambda);
% 注意:这里的特征向量要和特征值一一对应,之前特征值相当于颠倒过来了,因此特征向量
的各列需要颠倒过来
% rot90函数可以使一个矩阵逆时针旋转90度,然后再转置,就可以实现将矩阵的列颠倒的效果
V=rot90(V)';
对相关系数R进行可视化
-
①将R的数据复制到Excel表中,并设定行高为50
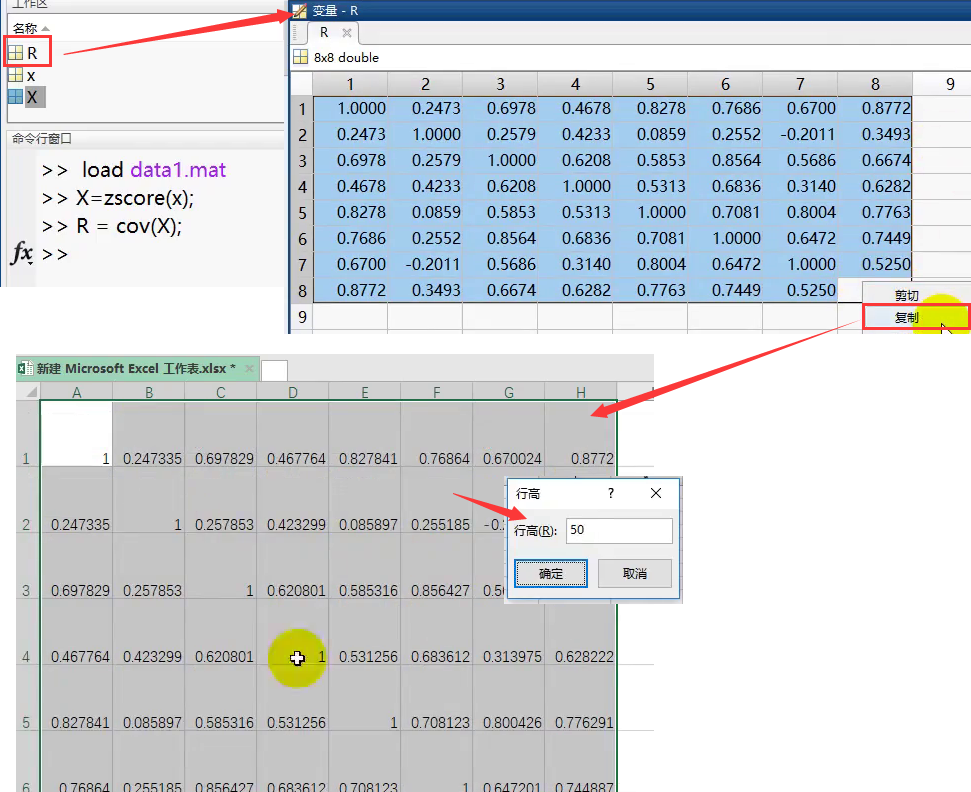
-
③色阶修改
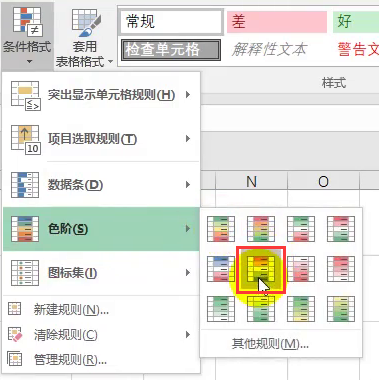
-
④管理规则(颜色越深代表相关性越强)
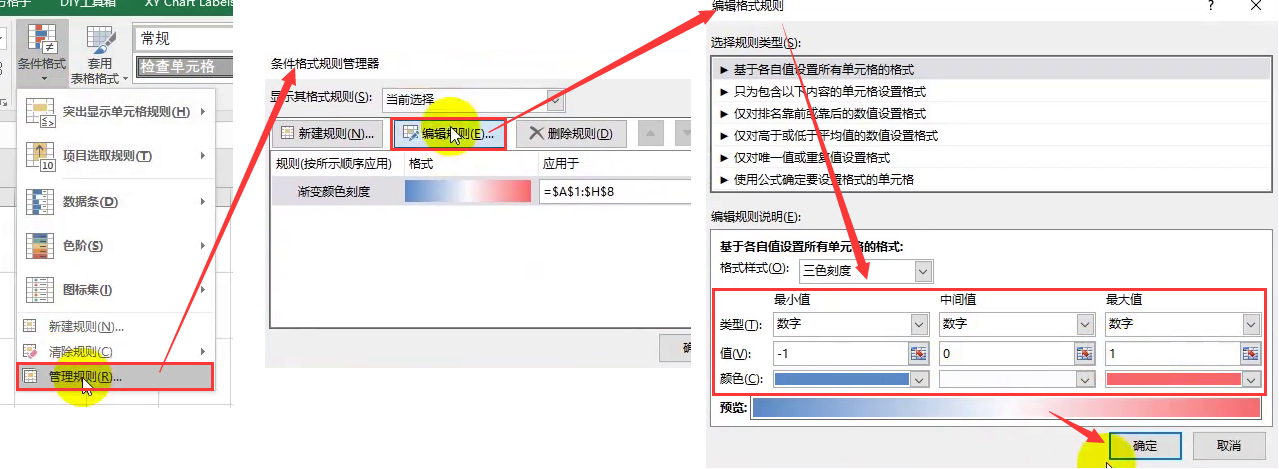
4.5 利用Matlab进行主成分分析
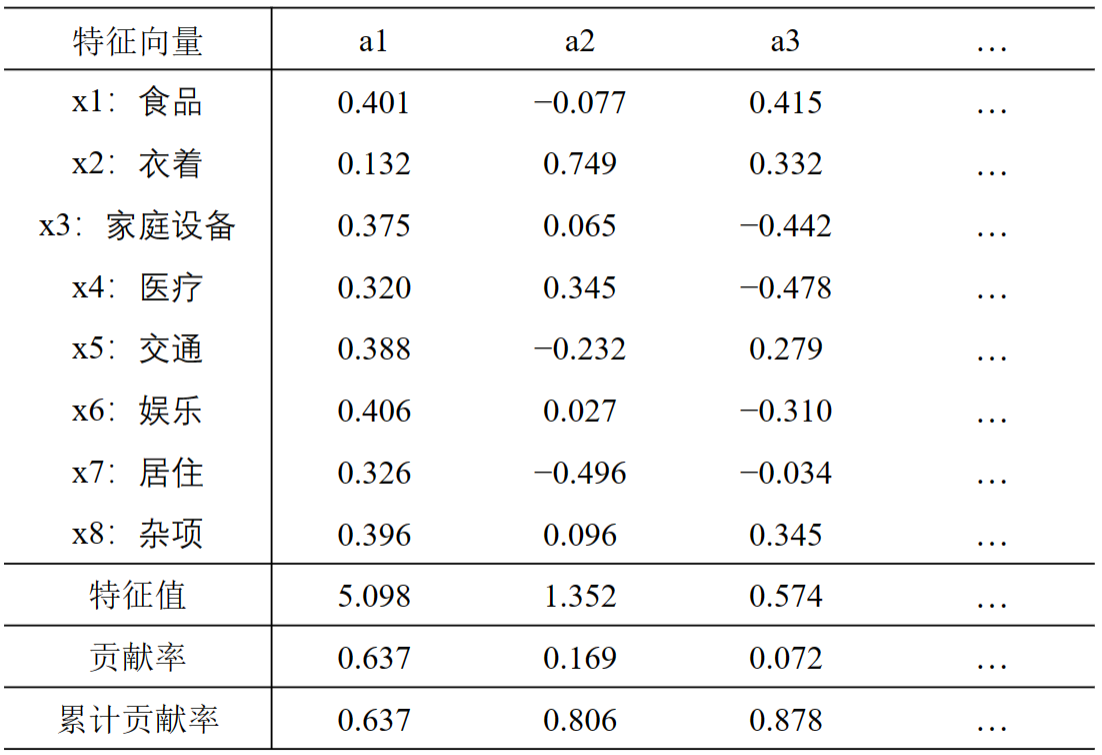
4.6 对结果的解释
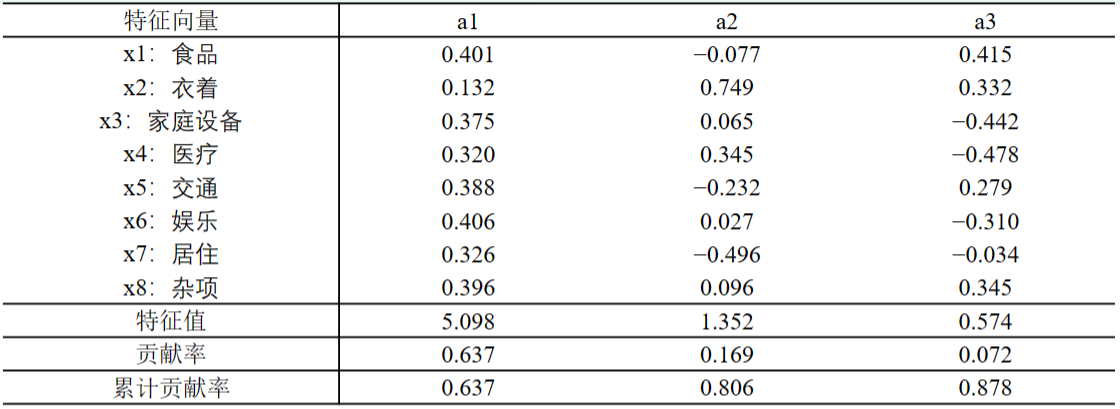
从上表可以看出,前两个和前三个主成分的累计贡献率分别达到80.6%和87.8%,第一主成分F1在所有变量(除在x2上的载荷稍偏小外)上都有近似相等的正载荷,反映了综合消费性支出的水平,因此第一主成分可称为综合消费性支出成分。第二主成分F2在变量x2上有很高的正载荷,在变量x4上有中等的正载荷,而在其余变量上有负载荷或很小的正载荷。可以认为这个主成分度量了受地区气候影响的消费性支出(主要是衣着 ,其次是医疗保健 )在所有消费性支出中占的比重(也可理解为一种消费倾向),第二主成分可称为消费倾向成分。第三主成分很难给出明显的解释,因此我们只取前面两个主成分。
五、主成分分析的滥用:主成分得分
-
①王学民老师

-
②清风老师的补充
- 主成分是降维算法,既然已经有数据了,为什么不把这些数据的信息全部用上呢?主成分分析是会损失原始数据的信息的。
- 指标可能有各种类型(极大、极小、区间等),主成分只有标准化的过程,并没有正向化的过程。
-
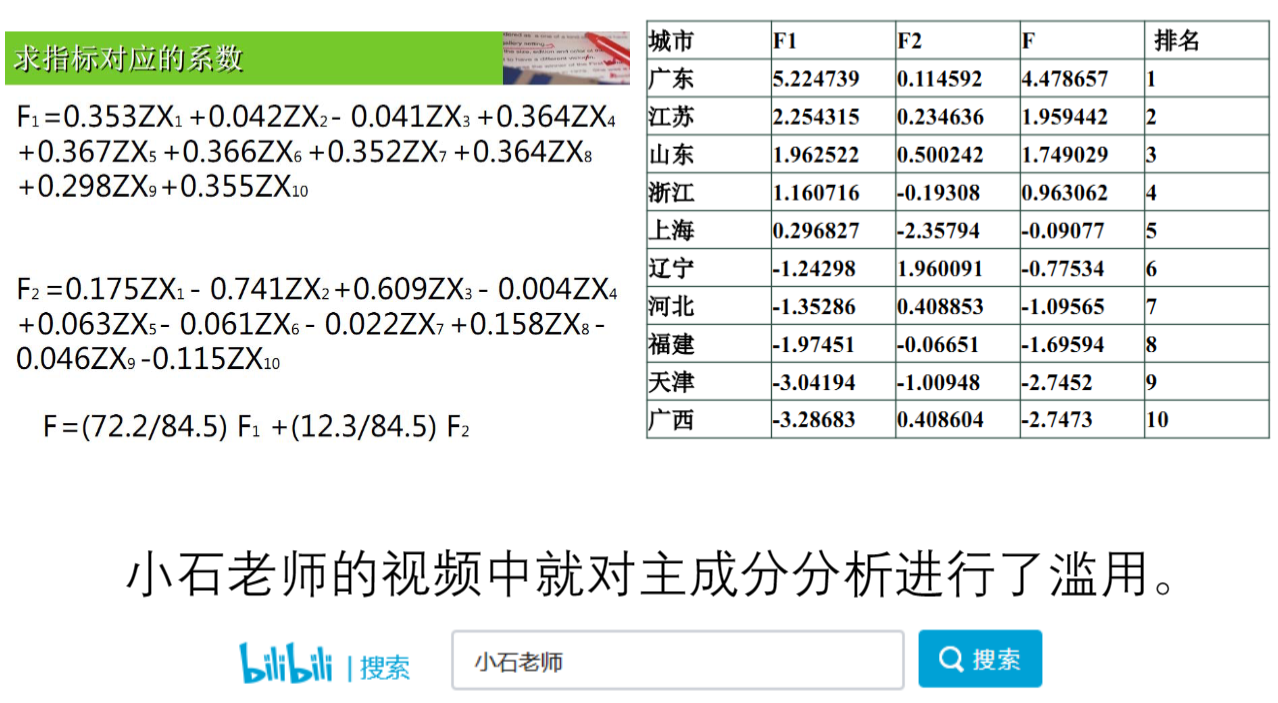
滥用的例子:
六、主成分分析用于聚类
-
Matlab生成结果复制进spss中
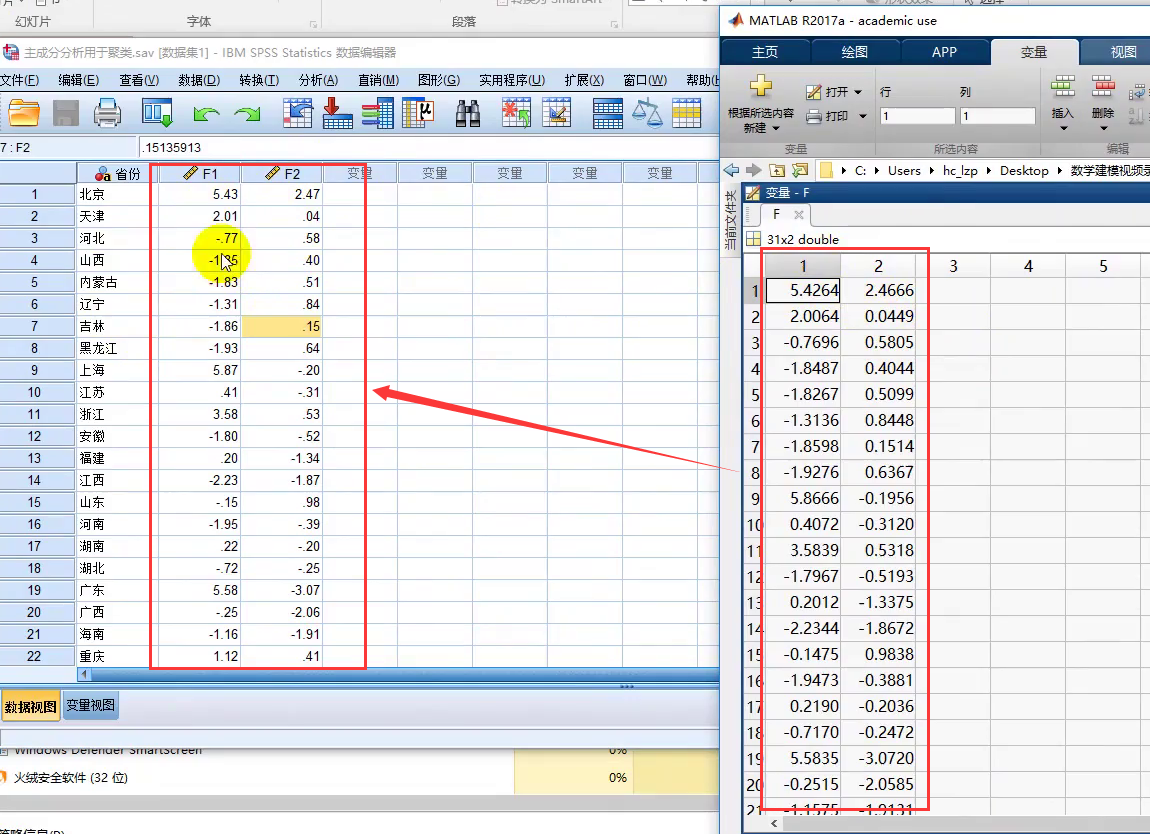
-
查看能大概分成几类:如下为3类
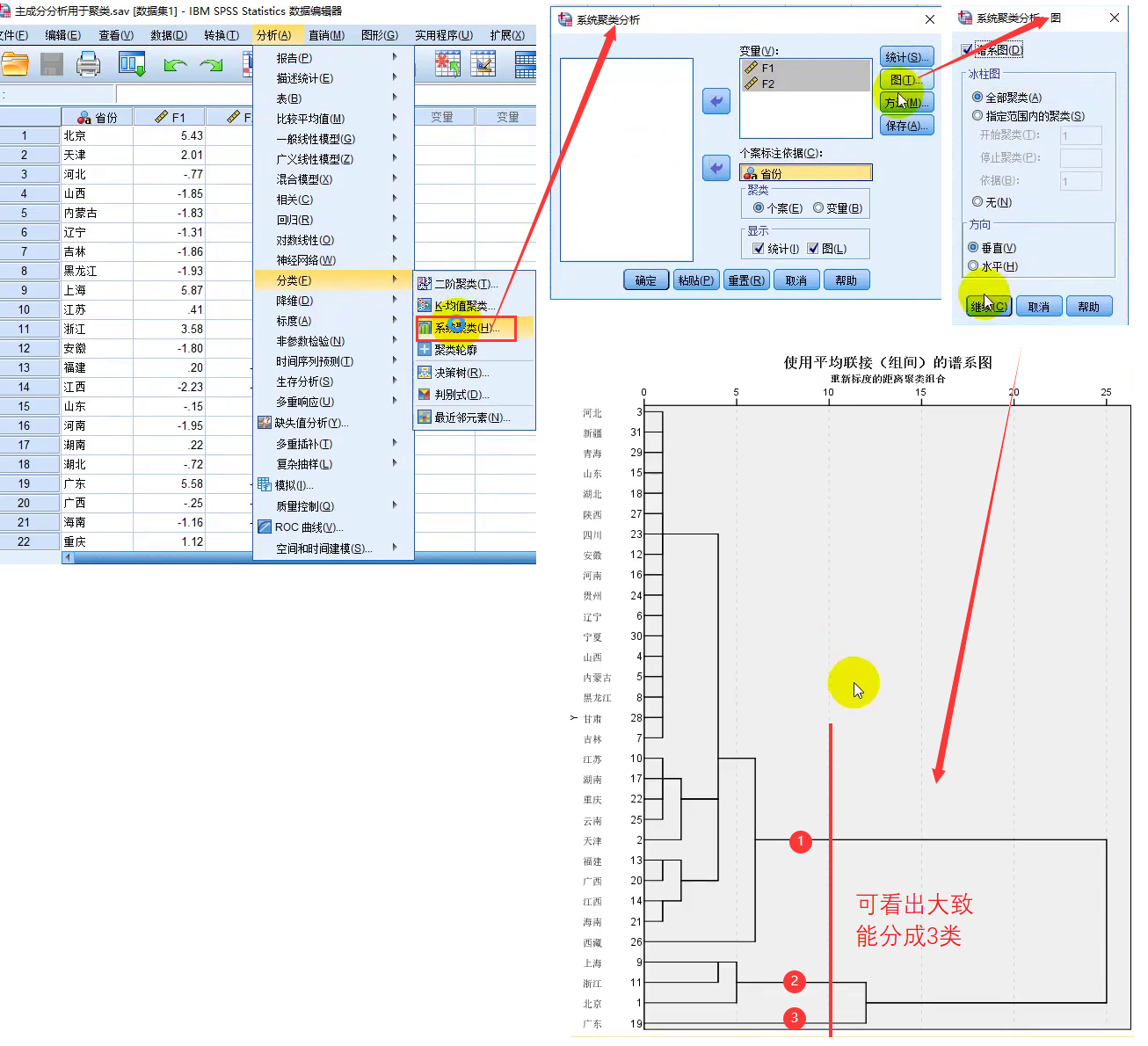
- 主成分和之前聚类模型对比生成的聚类结果:

- 主成分和之前聚类模型对比生成的聚类结果:
-
生成聚类效果图

-
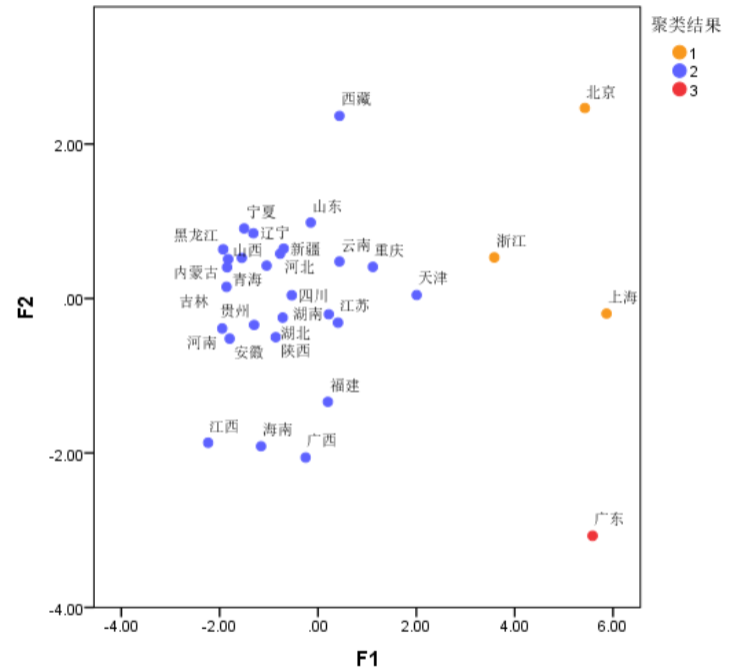
聚类效果图:主成分聚类最大的意义就是可视化最后的聚类效果,毕竟使用主成分是会降低部分信息的。(只有在指标个数特别多,且指标之间存在很强的相关性时才用主成分聚类。)
七、主成分回归
- 主成分回归可用来解决多重共线性的问题。
7.1 例题:探究棉花单产和五个指标之间的关系
7.2 主成分的解释
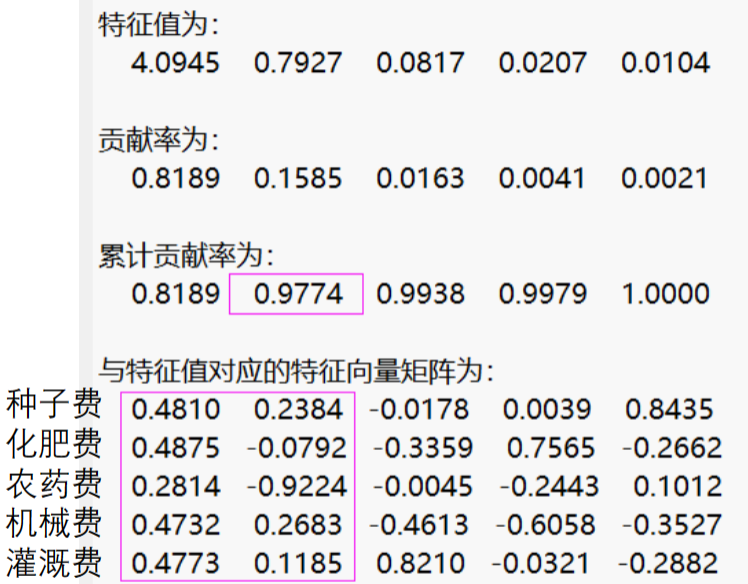
- 从表中可以看出,前两个主成分的累计贡献率为97.74%,第一主成分F1在所有变量(除在x3上的载荷稍偏小外)上都有近似相等的正载荷,反映了在种植投入上较为综合的水平,因此第一主成分可称为综合投入成分。第二主成分F2在变量x3(农药)上有很高的负载荷,在变量x2上有较低的负载荷,而在其余变量上均为正载荷。可以认为这个主成分度量了受土壤环境影响的投入(主要是农药 ,其次是机械费用 )在所有投入中占的比重。
7.3 在Stata中回归结果
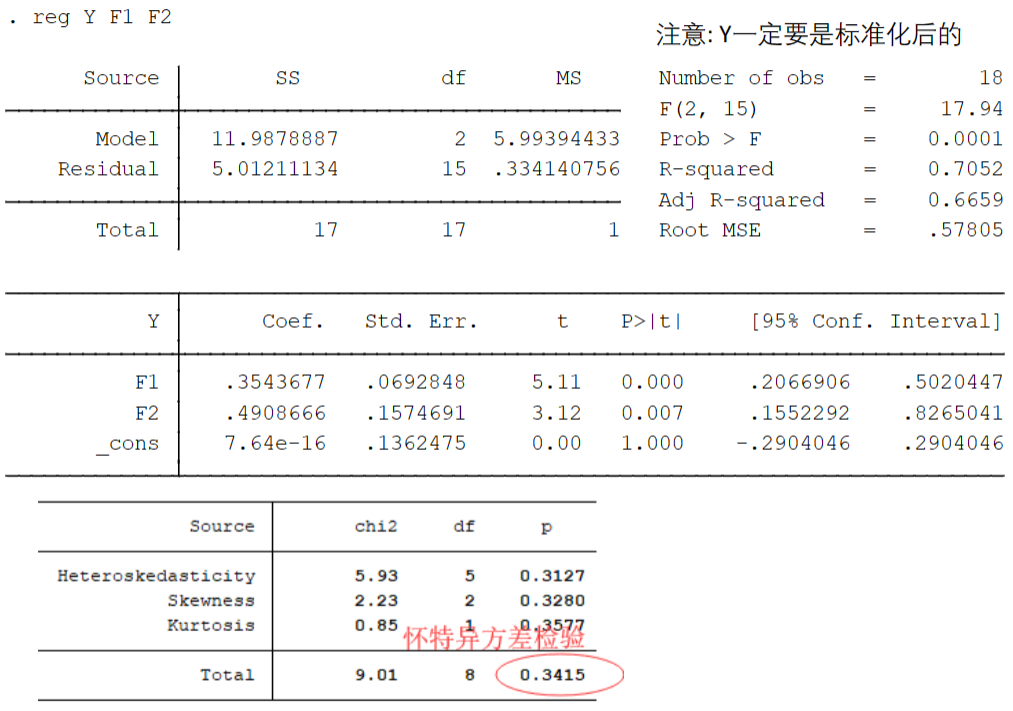
- Stata回归代码:
reg Y F1 F2 - Stata异方差检验代码:
estat imtest,white - 最重要解释回归系数,因为都是显著的
八、思考
- 问题1:之前学过逐步回归,逐步回归也可以用来解决多重共线性问题,该用逐步回归还是今天学习的主成分分析呢?
- 如果能够很好的解释清楚主成分代表的含义,那么建议在正文中既用主成分分析,又用逐步回归(多分析点没啥坏处,只要你能保证你不分析错就行);如果解释不清楚,还是用逐步回归。
- 问题2:主成分回归后,需要将原来的变量带回到回归方程吗?
- 没必要。因为要是代回去了,和普通的回归没什么区别。主成分的核心作用就是降维,代回去了维度也没降。
相关文章:

【数模】主成分分析PCA
主成分分析(Principal Component Analysis,PCA),是一种降维算法,它能将多个指标转换为少数几个主成分,这些主成分是原始变量的线性组合,且彼此之间互不相关,其能反映出原始数据的大部分信息。使用场景:一般…...

全志F1C200S嵌入式驱动开发(从DDR中截取内存)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing @163.com】 linux内核起来的时候,不一定所有的内存都是分配给linux使用的。有的时候,我们是希望能够截留一部分内存的。为什么保留这部分内存呢?这里面可以有很多的用途。比如说,第一,如果…...

C++中点云聚类算法的实现与应用探索
第一部分:C中点云聚类算法的实现与应用 在当今的计算机视觉领域,点云数据是一种重要的三维数据类型,它能有效表达三维物体的形状信息。然而,由于点云数据的无序性和稀疏性,对其进行分析与处理的难度较大。本文将介绍如…...

大数据Flink(五十六):Standalone伪分布环境(开发测试)
文章目录 Standalone伪分布环境(开发测试) 一、架构图 二、环境准备 三、下载安装包</...
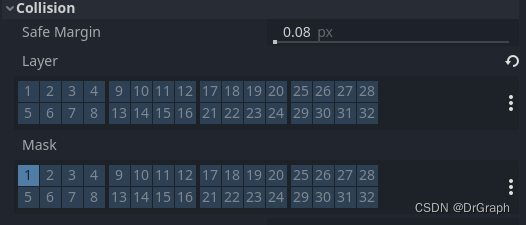
Godot 4 源码分析 - 碰撞
碰撞功能应该是一个核心功能,它能自动产生相应的数据,比如目标对象进入、离开本对象的检测区域。 基于属性设置,能碰撞的都具备这样的属性:Layer、Mask. 在Godot 4中,Collision属性中的Layer和Mask属性是用于定义碰撞…...

前端面试经典算法题
前言 现在面试流行考核算法,做过面试官,也被面试。问算法对面试官来说,是一种解脱,找出了一个看似很高明且能偷懒的办法选择人,避免了不知道问啥的尴尬;被面试者,也找到了一种新的面试八股文&am…...
ospf减少LSA更新
实验及实验要求 一、思路 1.根据区域划分IP地址 2.使公网可通---写缺省 3.使R3成为MGRE中心站点,R5、R6、R7为分支站点 4.一个个去配置ospf区域和RIP区域,确保每个区域配置无误 5.区域0要更改OSPF在接口的工作类型为broadcast ,并使R3为…...
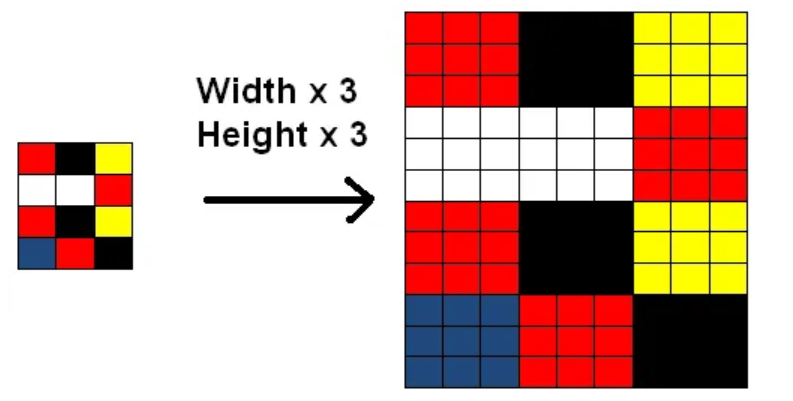
万字长文解析深度学习中的术语
引言 新手在学习深度学习或者在看深度学习论文的过程中,有不少专业词汇,软件翻译不出来,就算是翻译出来也看不懂,因为不少术语是借用其他学科的概念,这里整理了一些在深度学习中常见的术语,并对一些概念进…...

冠达管理投资前瞻:三星加码机器人领域 大信创建设提速
上星期五,沪指高开高走,盘中一度涨超1%打破3300点,但随后涨幅收窄;深成指、创业板指亦强势震动。截至收盘,沪指涨0.23%报3288.08点,深成指涨0.67%报11238.06点,创业板指涨0.95%报2263.37点&…...

24届近5年上海交通大学自动化考研院校分析
今天给大家带来的是上海交通大学控制考研分析 满满干货~还不快快点赞收藏 一、上海交通大学 学校简介 上海交通大学是我国历史最悠久、享誉海内外的高等学府之一,是教育部直属并与上海市共建的全国重点大学。经过120多年的不懈努力,上海交…...
【PDF密码】PDF文件不能打印,为什么?
正常的PDF文件是可以打印的,如果PDF文件打开之后发现文件不能打印,我们需要先查看一下自己的打印机是否能够正常运行,如果打印机是正常的,我们再查看一下,文件中的打印功能按钮是否是灰色的状态。 如果PDF中的大多数功…...

LeetCode-Java(03)
9. 回文数 class Solution {public boolean isPalindrome(int x) {if (x < 0 || (x % 10 0 && x ! 0)) {return false;}int revertedNumber 0;while (x > revertedNumber) {revertedNumber revertedNumber * 10 x % 10;x / 10;}// 当长度为奇数时通过reverte…...

【Linux命令行与Shell脚本编程】第十六章 Shell函数
Linux命令行与Shell脚本编程 第一章 文章目录 Linux命令行与Shell脚本编程六.函数6.1.脚本函数基础6.1.1.创建函数6.1.2.使用函数 6.2.函数返回值6.2.1.默认的退出状态码6.2.2.使用return命令6.2.3.使用函数输出 6.3.函数中使用变量6.3.1.向函数传递参数6.3.2.在函数中处理变量…...
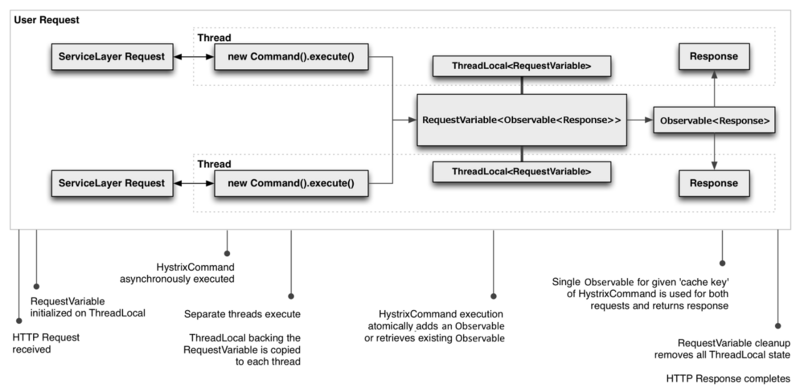
SpringCloud-Hystrix服务熔断与降级工作原理源码 | 京东物流技术团队
先附上Hystrix源码图 在微服务架构中,根据业务来拆分成一个个的服务,服务与服务之间可以相互调用(RPC),在Spring Cloud可以用RestTemplateRibbon和Feign来调用。为了保证其高可用,单个服务通常会集群部署。…...
react脚手架)
(一)react脚手架
1. react脚手架 react提供了一个用于创建react项目的脚手架库:create-react-app 项目的整体技术架构为:react webpack es6 eslint 使用脚手架开发的项目的特点:模块化、组件化、工程化 2. 创建项目并启动 # 第一步: 全局安…...

Typescript中的元组与数组的区别
Typescript中的元组与数组的区别 元组可以应用在经纬度这样明确固定长度和类型的场景下 //元组和数组类似,但是类型注解时会不一样//元组赋值的类型、位置、个数需要和定义的类型、位置、个数完全一致,不然会报错。 // 数组 某个位置的值可以是注解中的…...
SpringBoot的index首页的访问、自定义Favicon图标
目录 1. index首页1.1 index首页访问规则的源码1.2 index首页的访问 2. 自定义Favicon图标 1. index首页 1.1 index首页访问规则的源码 package org.springframework.boot.autoconfigure.web.servlet; ......省略部分......// SpringBoot给容器中放WebMvcConfigurationSuppor…...
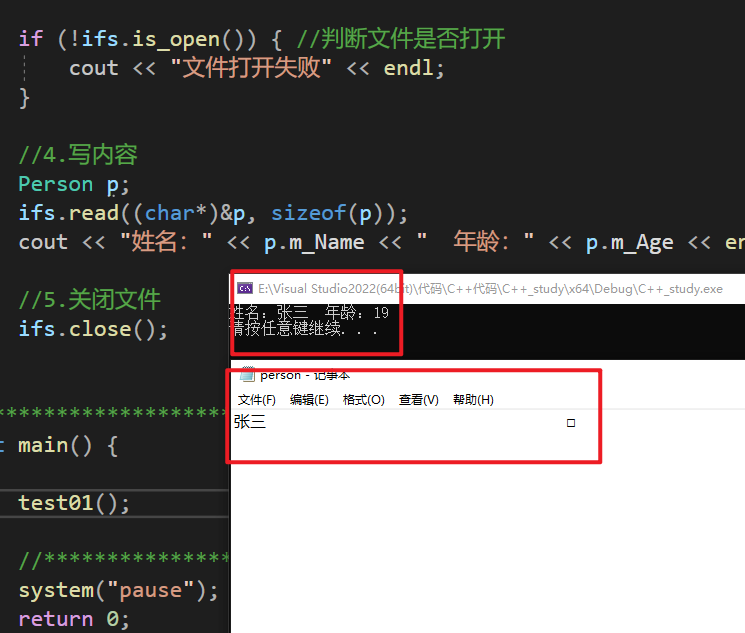
【C++】C++文件操作-文本文件/二进制文件
0.前言 一、文本文件 1.写文件 代码 #include <iostream> using namespace std; #include <fstream> //头文件包含//************************************** //文本文件 写文件 void test01() {//1.包含文件 fstream//2.创建流对象ofstream ofs;//3.指导打开方式…...

java通过http网络url下载文件
Testpublic void test3() throws ParseException {String fileUrl "http://*****/123.pdf";String savePath "C:\\Users\\HHH\\Desktop\\文件\\123.pdf";try {URL url new URL(fileUrl);InputStream inputStream url.openStream();Path outputPath Pa…...

网络安全【黑客】自学
1.什么是网络安全? 网络安全可以基于攻击和防御视角来分类,我们经常听到的 “红队”、“渗透测试” 等就是研究攻击技术,而“蓝队”、“安全运营”、“安全运维”则研究防御技术。 无论网络、Web、移动、桌面、云等哪个领域,都有…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...
