.net core 依赖注入生命周期
在.NET Core中,依赖注入的生命周期用于控制注入的服务实例的生命周期。下面是.NET Core中常用的几种依赖注入生命周期:
-
Singleton(单例):在整个应用程序生命周期内只创建一个实例。每次注入都返回同一个实例。示例代码:
services.AddSingleton<IService, Service>(); -
Scoped(作用域):在每个作用域内创建一个实例。通常是在每个请求或操作中创建一个实例。在同一个作用域内,每次注入都返回同一个实例。示例代码:
services.AddScoped<IService, Service>(); -
Transient(临时):每次注入都创建一个新的实例。没有共享实例,每次注入都会返回一个新的实例。示例代码:
services.AddTransient<IService, Service>();
使用场景:
-
如果服务是无状态的,并且在整个应用程序中共享使用,可以选择 Singleton 生命周期。例如,一些静态配置或连接对象。
-
如果服务需要在每个请求或操作中保持一致性,可以选择 Scoped 生命周期。例如,一些数据库上下文或工作单元。
-
如果服务是轻量级的且可被多次创建,可以选择 Transient 生命周期。例如,简单的计算逻辑或服务代理。
需要注意的是,生命周期的选择会影响应用程序的性能和内存使用。如果使用不当,可能会导致内存泄漏或性能问题。选择适当的生命周期非常重要,确保在不同的场景下使用适当的服务生命周期。
相关文章:

.net core 依赖注入生命周期
在.NET Core中,依赖注入的生命周期用于控制注入的服务实例的生命周期。下面是.NET Core中常用的几种依赖注入生命周期: Singleton(单例):在整个应用程序生命周期内只创建一个实例。每次注入都返回同一个实例。示例代码…...
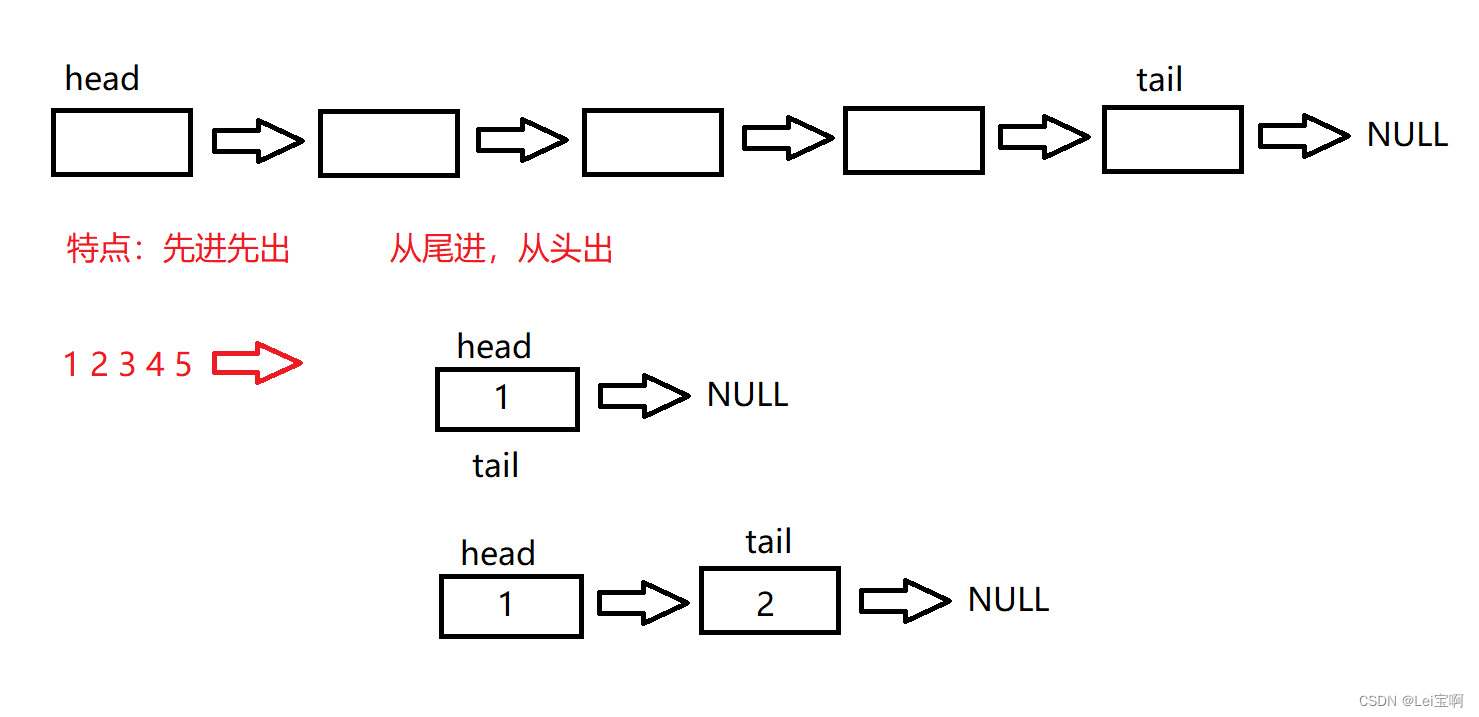
栈和队列的实现
Lei宝啊:个人主页(也许有你想看的) 愿所有美好不期而遇 前言 : 栈和队列的实现与链表的实现很相似,新瓶装旧酒,没什么新东西。 可以参考这篇文章: -------------------------无头单向不循环…...

java中的垃圾收集机制
推荐 1 1 垃圾回收 1.1 java的gc堆中的对象而言,什么时候对象会从待回收状态变为激活状态(垃圾变成非垃圾对象) 当然可以。首先,为了使用 try-with-resources,您需要一个实现了 AutoCloseable 或 Closeable 接口的…...

TCP网络服务器设计
最近设计了一个网络服务器程序,对于4C8G的机器配置,TPS可以达到5W。业务处理逻辑是简单的字符串处理。服务器接收请求后对下游进行类似广播的发送。在此分享一下设计方式,如果有改进思路欢迎大家交流分享。 程序运行在CentOS7.9操作系统上&a…...

4. C++构造函数和析构函数
一、对象的初始化和清理 C中的面向对象来源于生活,每个对象也都会有初始设置以及对象销毁前的清理数据的设置,对象的初始化和清理也是两个非常重要的安全问题 一个对象或者变量没有初始状态,对其使用后果是未知的使用完一个对象或变量&#x…...

【Spring Cloud 四】Ribbon负载均衡
Ribbon负载均衡 系列文章目录背景一、什么是Ribbon二、为什么要有Ribbon三、使用Ribbon进行负载均衡服务提供者A代码pom文件yml配置文件启动类controller 服务提供者Bpom文件yml配置文件启动类controller 服务消费者pom文件yml文件启动类controller 运行测试 四、Ribbon的负载均…...

“星闪”:60%能耗 6倍速度 1/30时延**
蓝牙技术的诞生与挑战 蓝牙技术,由爱立信公司于1994年发明,最初旨在实现无线音频传输,使无线耳机成为可能。这项技术成为过去20多年里最主流的近距离无线通讯技术,广泛应用于手机、耳机、手柄、键盘等设备。然而,尽管…...

cocosCreator 之 i18n多语言插件
版本: v3.4.0 环境: Mac 简介 i18n是国际化的简称, 全名:internationalization;取首尾字符i和n,18代表单词中间的字符数目。 该插件不需要产品做太多的改变,通过语言的设置,实现不…...

redis 如何保证数据一致性
前言 日常开发中常会使用redis作为项目中的缓存,只要我们使用 Redis 缓存,就必然会面对缓存和数据库间的一致性保证问题。而且如果数据不一致,那么应用从缓存中读取的数据就不是最新数据,可能会导致严重的业务问题。 为什么会数…...
因果推断(三)双重差分法(DID)
因果推断(三)双重差分法(DID) 双重差分法是很简单的群体效应估计方法,只需要将样本数据随机分成两组,对其中一组进行干预。在一定程度上减轻了选择偏差带来的影响。 因果效应计算:对照组y在干预…...
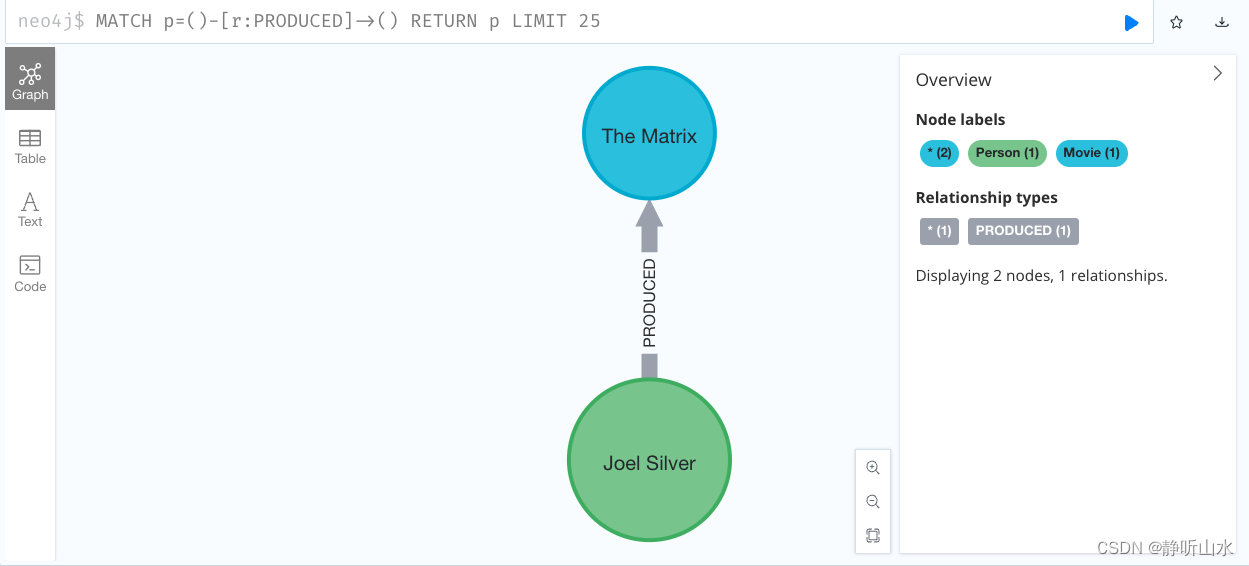
neo4j入门实例介绍
使用Cypher查询语言创建了一个图数据库,其中包含了电影《The Matrix》和演员Keanu Reeves、Carrie-Anne Moss、Laurence Fishburne、Hugo Weaving以及导演Lilly Wachowski和Lana Wachowski之间的关系。 CREATE (TheMatrix:Movie {title:The Matrix, released:1999,…...

CGAL-2D和3D线性几何内核-点和向量-内核扩展
文章目录 1.介绍1.1.鲁棒性 2.内核表示2.1.通过参数化实现泛型2.2.笛卡尔核2.3.同质核2.4.命名约定2.5.内核作为trait类2.6.选择内核和预定义内核 3.几何内核3.1.点与向量3.2.内核对象3.3.方位和相对位置 4.谓语和结构4.1.谓词4.2.结构4.3.交集和变量返回类型4.4.例子4.5.构造性…...

Ubuntu 22.04 安装docker
参考: https://docs.docker.com/engine/install/ubuntu/ 支持的Ubuntu版本: Ubuntu Lunar 23.04Ubuntu Kinetic 22.10Ubuntu Jammy 22.04 (LTS)Ubuntu Focal 20.04 (LTS) 1 卸载旧版本 非官方的安装包,需要先卸载: docker.io…...

电脑维护进阶:让你的“战友”更强大、更持久!
前言 无论是学习还是工作,电脑已经成为了IT人必不可少的得力助手。然而,电脑的性能和寿命需要经过细心的维护来保证。本文将详细探讨如何维护你的电脑,延长它的寿命,以及一些实用建议。 硬件保养篇 内部清洁 灰尘会导致电脑散热…...

【Leetcode】75.颜色分类
一、题目 1、题目描述 给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。 我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。 必须在不使用库内置的 sort 函数的情况下解决这个问…...

Pytesseract学习笔记
函数 pytesseract.image_to_string(image: Any, lang: Any None, …) 识别图像中的文本。 Parameters image(Any):输入图像,不接受bytes类型。...
cnvd通用型证书获取姿势
因为技术有限,只能挖挖不用脑子的漏洞,平时工作摸鱼的时候通过谷歌引擎引擎搜索找找有没有大点的公司有sql注入漏洞,找的方法就很简单,网站结尾加上’,有异常就测试看看,没有马上下一家,效率至上…...

elasticsearch的副本和分片的区别
es/elasticsearch的副本和分片的区别 一:概念 (1)集群(Cluster): ES可以作为一个独立的单个搜索服务器。不过,为了处理大型数据集,实现容错和高可用性,ES可以运行在许多互…...

Docker部署Gitlab
Docker部署Gitlab 文章目录 Docker部署Gitlab前置环境部署步骤初始化配置文件80端口部署方式(二选一)非80端口需要的部署方式(二选一)修改 gitlab.rb修改 gitlab.yml刷新配置 前置环境 docker 19.03.13 es 7.2.0 部署步骤 初始…...

ABeam News | ABeam大中华区新人入社式,开启崭新的职场探索之旅吧!
ABeam News | ABeam大中华区新人入社式,开启崭新的职场探索之旅吧! 隔空投送 很高兴认识你 7月3日,FY24 ABeam大中华区新人入社式在西安隆重举办,ABeam大中华区董事长兼总经理中野洋辅先生专程莅临入社式现场,与89名…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...
