42.利用 牛顿迭代法解非线性高维方程组(matlab程序)
1.简述
若向量记号为X,方程组就可以写成F(X)=0的形式。
我们知道,对于一元函数的牛顿迭代法求根公式
类似的,对于多元函数求根公式
其中X是向量,是非线性方程组对应的雅可比矩阵。
具体求解的时候,我们可以先通过绘图命令绘制图形,看交点。然后将交点附近的值带入迭代
矩阵。最后求出小于误差的收链解。
2.代码
主程序:
function newton%牛顿迭代法解非线性方程组
syms a x;
beta=0.15;
F=[1-beta+sqrt((1-beta)^2+4*a)-2*x;
beta+a+2*x-(beta+x)^3];
eps=10e-6;%精度
num=1;%记步数
tol=1;%给定误差初始值
x0=[1;1];%参数赋初始值
v=[a,x];
while tol>eps
Fx=subs(F,v,transpose(x0));
dF=jacobian(F,v);
c=subs(dF,v,transpose(x0));
x=x0-inv(c)*Fx;
tol=norm(x-x0);
x0=x;
num=num+1;
if (num>10^8)
disp('迭代次数大于最大值,可能不收敛')
return
end
end
%Output
fprintf('解出 a = %g.\n',x0(1))
fprintf('解出 x = %g.\n',x0(2))
fprintf('迭代次数 n = %g次.\n',num)
子程序:
function [y,n]=newton_fun(F,x0)
if nargin==2
eps=1.0e-6;
end
num = 0;
tol = 1;
v=findsym(F);
while tol>eps
Fx = subs(F,v,transpose(x0));
dF=jacobian(F,v);
c=subs(dF,v,transpose(x0));
x=x0-inv(c)*Fx;
tol=norm(x-x0);
x0=x;
num=num+1;
if (num>10^8)
disp('迭代次数大于最大值,可能不收敛')
return
end
end
y = x0;
n = num;
end
子程序:
function solve
syms x
gamma=0.5;
m=5;
theta=12;
a=1-gamma;
F=sin((m+1)*x)-a*sin(m*x);
for i=0:m+1
w0=i*pi/(m+1);
[x,n]=newton_fun(F,w0);
w(i+1)=x;
% beta(i+1)=theta*gama^2/(sqrt(1+a^2-2*a*cos(x))-gama*(1-theta));
b(i+1)=cos((m+1)*x)-a*cos(m*x);%先算出b
beta(i+1)=theta*gamma^2/(b(i+1)-gamma*(1-theta));%再算出beta
num(i+1)=n;
end
w
beta
num
相关文章:
)
42.利用 牛顿迭代法解非线性高维方程组(matlab程序)
1.简述 若向量记号为X,方程组就可以写成F(X)0的形式。 我们知道,对于一元函数的牛顿迭代法求根公式 类似的,对于多元函数求根公式 其中X是向量,是非线性方程组对应的雅可比矩阵。 具体求解的时候,我们可以先通过绘图命令绘制图形…...

我在leetcode用动态规划炒股
事情是这样的,突然兴起的我在letcode刷题 121. 买卖股票的最佳时机122. 买卖股票的最佳时机 II123. 买卖股票的最佳时机 III 以上三题。 1. 121. 买卖股票的最佳时机 1.1. 暴力遍历,两次遍历 1.1.1. 算法代码 public class Solution {public int Ma…...

rust实践-异步并发socket通信
客户端 [package] name = "rust_client" version = "0.1.0" edition = "2021"[dependencies] tokio = {version = "1.14.0", features = ["full"] }use tokio::io::{self, AsyncReadExt, AsyncWriteExt}; use tokio::net::…...

SolidUI社区-根据Prompt打造人设
背景 随着文本生成图像的语言模型兴起,SolidUI想帮人们快速构建可视化工具,可视化内容包括2D,3D,3D场景,从而快速构三维数据演示场景。SolidUI 是一个创新的项目,旨在将自然语言处理(NLP)与计算机图形学相…...
设计模式行为型——观察者模式
目录 什么是观察者模式 观察者模式的实现 观察者模式角色 观察者模式类图 观察者模式举例 观察者模式代码实现 观察者模式的特点 优点 缺点 使用场景 注意事项 实际应用 什么是观察者模式 观察者模式(Observer Pattern)是一种行为型设计模式…...

Kernel Exception导致手机重启案例分析
和你一起终身学习,这里是程序员Android 经典好文推荐,通过阅读本文,您将收获以下知识点: 一、高温触发 Kernel Exception 重启问题二、解决方案三、提高电池温度方案 一、 高温触发 Kernel Exception 重启问题 手机 电池温度 默认60度以上高温…...
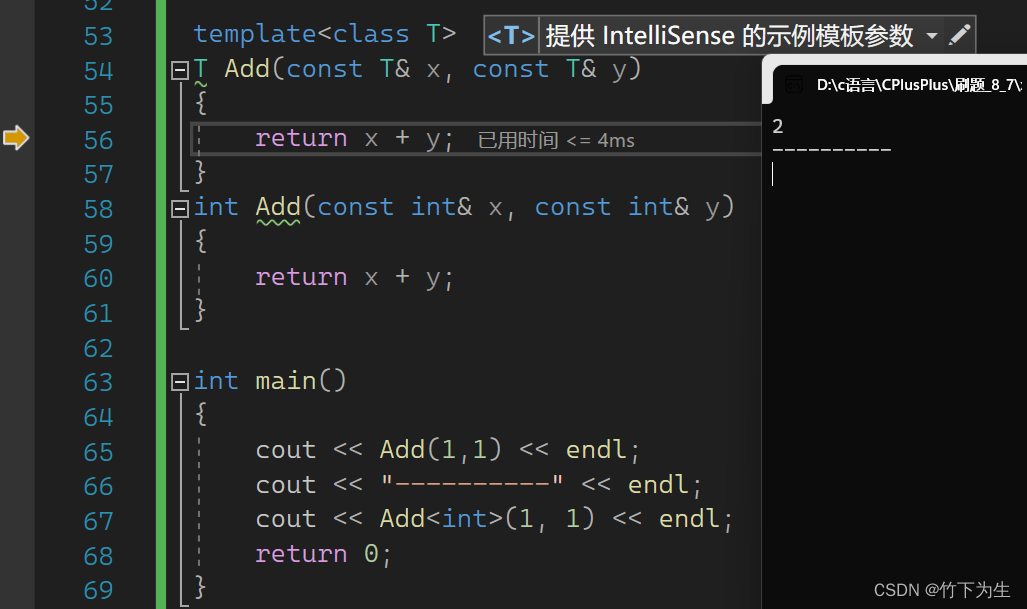
C++入门篇5---模板
相信大家都遇到过这么一种情况,为了满足不同类型的需求,我们要写多个功能相同,参数类型不同的代码,为此,C引入了泛型编程这一概念,而模板就是实现泛型编程的基础,其实本质就是我们写一个类似”模…...

L2CS-Net: 3D gaze estimation
L2CS-Net: Fine-Grained Gaze Estimation in Unconstrained Environments论文解析 摘要1. 简介2. Related Work3. METHOD3.1 Proposed loss function3.2 L2CS-Net 结构3.3 数据集3.4 评价指标 4. 实验4.1 实验结果 论文地址:L2CS-Net: Fine-Grained Gaze Estimation…...

kenernetes/k8s笔试面试
k8s的基础概念 k8s本质是一个容器编排系统,可以管理容器的生命周期,应用部署,更新,维护,应用提供服务,扩容缩容应用,故障自愈。 k8s与docker的关系 docker:是一种轻量级的虚拟化技术。运维层…...

我们真的是在做数据治理吗
我们真的是在做数据治理吗? 什么是数据治理? 数据治理和数据管理有什么区别? 相信即使是考过数据治理工程师的人,面对这2个问题也仍然会有这个疑问。 目前国际和国内对于数据治理没有明确统一的定义,对于数据治理的服…...

聊聊汽车电子的话题
当谈到汽车电子时,有许多有趣的话题可以探讨。以下是一些可能感兴趣的话题: 自动驾驶技术:自动驾驶技术正变得越来越先进,它们如何在汽车中实现?它们将如何改变我们的交通方式以及对道路安全的影响? 电动汽…...

ThinkPHP6企业OA办公系统
有需要请加文章底部Q哦 可远程调试 ThinkPHP6企业OA办公系统 一 介绍 勾股OA基于ThinkPHP6开发,前端Layui,数据库mysql,是一款实用的企业办公系统。可多角色登录,集成了系统设置、人事管理、消息管理、审批管理、日常办公、客户…...
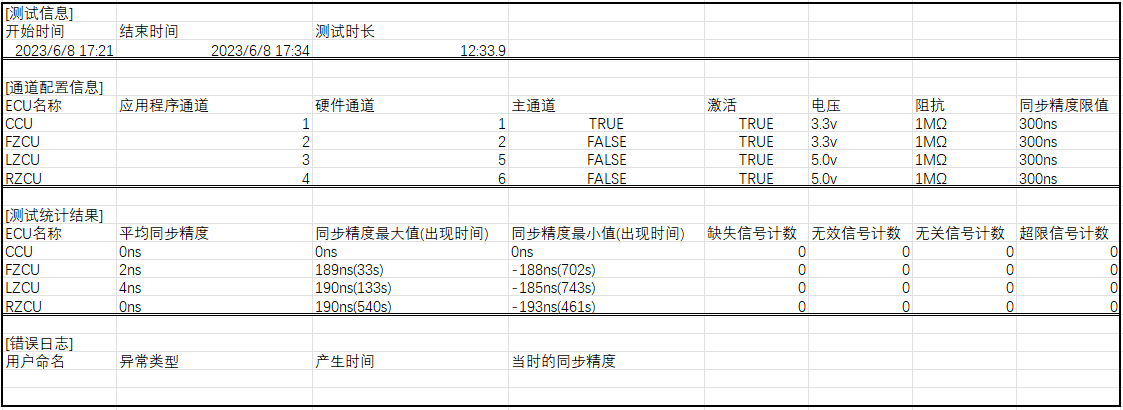
PPS Tester测量原理和实施方法
怿星科技发布了新品PPS Tester,这是一款基于1PPS方法的时间同步精度测试设备。PPS Tester由硬件模块ETS2110和上位机软件ePPSTester构成。本文将围绕此设备的应用场景,介绍相关概念和设备使用方法。 什么是时间同步? 时间同步就是采取某项技…...
浅谈新电改背景下电网企业综合能源服务商业模式研究及发展方向
安科瑞 华楠 摘要: 新电改方案实施后,由于输配电价的改革和售电侧的放开,电网企业的盈利模式也随之发生了变化。这就要求电网企业转变服务理念与经营方式,来寻求竞争优势。基于“魏朱六要素商业模式”模型,对电网企业综合能源服务…...

SpringBoot + Docker 实现一次构建到处运行~
一、容器化部署的好处 图片 Docker 作为一种新兴的虚拟化方式,它可以更高效的利用系统资源,不需要进行硬件虚拟以及运行完整操作系统等额外开销。 传统的虚拟机技术启动应用服务往往需要数分钟,而 Docker 容器应用,由于直接运行…...

clang-format格式化代码
1. clang-format简介 Clang-Format可用于格式化(排版)多种不同语言的代码。其自带的排版格式主要有:LLVM, Google, Chromium, Mozilla, WebKit等; 利用style参数配置风格。通过编写 .clang-format 文件,可以实现代码风格的配置。…...

品牌宣传与媒体传播是声誉管理的主要方式之一
企业声誉是现如今影响品牌信任度、客户忠诚度的重要因素,也被视为企业的一种无形资,更影响着企业未来的发展。因此,企业声誉管理也日渐成为企业管理的重要课题之一,尤其在品牌营销管理领域。 什么是声誉管理?声誉管理有…...
)
2023年8月7日-8月13日,(上午熟悉公司代码,周一到周五晚上优先工作所急视频教程,其他业余时间进行ue视频教程,为独立游戏做准备)
按照规划,上午熟悉公司源码,下午进行filament和ue渲染,晚上写工作代码。回家后泛读pbrt或者其他书籍催眠。 业余学习ue的各种视频教程,为独立游戏做准备(公司也实行末位淘汰,给自己留条后路)。累…...

Vue3 第二节 Vue3的响应式
1.Vue3的响应式原理 2.ref函数和reactive函数的对比 3.setup注意点 一.Vue3的响应式原理 1.Vue2.x中的响应式原理 ① 实现原理 对象类型:通过Object.defineProperty() 对属性的读取,修改进行拦截(数据劫持)数组类型…...
通过easyui实现动态控制表格字段显示、导出表格数据
前言 学过layui前端框架的都知道,layui默认帮我们实现了控制表格字段显示以及数据的导出功能。 1、控制表格字段显示 2、数据导出 3、导出为pdf:导出按钮的右边那个按钮就是打印pdf的 那么,easyui要怎么实现这些功能呢?这篇文章就…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...
