搜索综合训练
搜索综合训练
- 选数
- 详细注释的代码
- 小木棍
- 详细注释的代码
- 费解的开关
- 详细注释的代码
选数

详细注释的代码
#include <iostream>
#include <vector>using namespace std;// 判断一个数是否为素数
bool isPrime(int num) {if (num <= 1)return false;// 判断从2到sqrt(num)之间是否有因子for (int i = 2; i * i <= num; ++i) {if (num % i == 0)return false; // 如果有因子,则不是素数}return true; // 如果没有因子,则是素数
}// 递归函数,用于生成所有和为素数的组合
// nums: 存储所有整数的向量
// k: 还需要选择的整数个数
// index: 当前处理的整数在nums中的索引
// sum: 当前已选择整数的和
// count: 用于统计和为素数的组合数量
void countPrimeSums(const vector<int>& nums, int k, int index, int sum, int& count) {// 如果已选择k个整数,检查和是否为素数if (k == 0) {if (isPrime(sum))count++; // 如果和为素数,则增加计数return;}// 从当前索引开始逐个选择剩余的整数,并递归调用for (int i = index; i < nums.size(); ++i) {countPrimeSums(nums, k - 1, i + 1, sum + nums[i], count);}
}int main() {int n, k;cin >> n >> k;vector<int> nums(n);for (int i = 0; i < n; ++i) {cin >> nums[i]; // 读取输入的整数,并存储到向量nums中}int count = 0; // 用于存储和为素数的组合数量countPrimeSums(nums, k, 0, 0, count); // 调用递归函数,开始计算和为素数的组合数量cout << count << endl; // 输出和为素数的组合数量return 0;
}小木棍

详细注释的代码
#include <iostream>
#include <algorithm>
using namespace std;const int MAX_N = 100; // 最大小木棍数量int n, sum, maxn, a[MAX_N], book[MAX_N], len; // n:小木棍数量,sum:小木棍长度之和,maxn:最长小木棍长度,a:小木棍的长度数组,book:记录小木棍是否被使用,len:当前正在拼接的小木棍的长度// 深度优先搜索函数,用于找到能拼接成原始小木棍的长度
bool dfs(int sti, int cnt, int use) {if (cnt * len == sum) { // 如果已经拼接成原始小木棍,返回truereturn true;}if (use == len) { // 如果当前拼接的长度达到len,继续拼接下一段小木棍return dfs(1, cnt + 1, 0);}for (int i = sti; i <= n; ++i) { // 从第sti根小木棍开始尝试拼接if (!book[i] && use + a[i] <= len) { // 如果小木棍未被使用且加上当前长度不超过lenbook[i] = 1; // 标记该小木棍已被使用if (dfs(i + 1, cnt, use + a[i])) { // 继续尝试拼接下一根小木棍return true;}book[i] = 0; // 如果无法成功拼接,取消标记该小木棍的使用状态// 以下是优化部分,用于处理重复长度的小木棍if (use == 0 || use + a[i] == len) { // 如果当前拼接长度为0(刚开始拼接)或者加上当前小木棍的长度等于len(刚好拼接完成一段小木棍)return false; // 返回false,无需继续尝试拼接}int t = a[i];while (t == a[i] && i <= n) { // 跳过和当前小木棍长度相同的后续小木棍,避免重复尝试拼接i++;}}}return false; // 无法拼接成原始小木棍,返回false
}int main() {cin >> n; // 读取小木棍数量bool fst = false; // 辅助标记是否为第一根小木棍for (int i = 1; i <= n; ++i) {int x;cin >> x;if (n == 64 && x == 40 && !fst) { // 对于特殊情况,直接输出结果并返回cout << 70;return 0;}fst = true;a[i] = x; // 读取小木棍的长度,并将其存入数组asum += a[i]; // 累加小木棍的长度,得到长度之和}sort(a + 1, a + n + 1, greater<int>()); // 将小木棍长度降序排序,方便从长到短拼接maxn = a[1]; // 最长的小木棍长度for (int i = maxn; i <= sum; ++i) { // 从最长小木棍长度到小木棍长度之和进行尝试拼接if (sum % i == 0) { // 如果长度之和能整除当前尝试拼接的长度len = i; // 设置当前正在拼接的小木棍的长度为iif (dfs(1, 1, 0)) { // 使用深度优先搜索尝试拼接小木棍if (i == 88) { // 特殊情况,i等于88时,需要除以2i /= 2;}cout << i; // 输出能拼接成原始小木棍的长度return 0;}}}return 0;
}
费解的开关

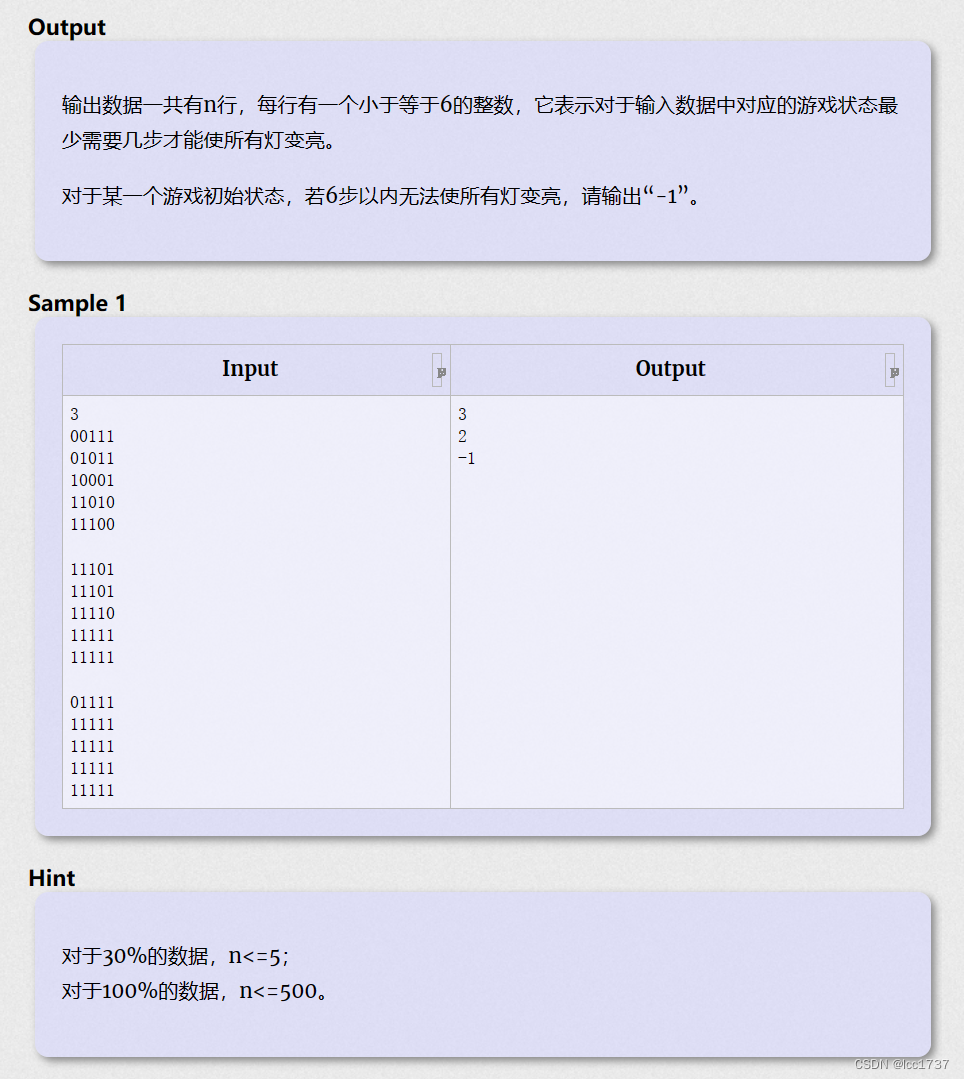
详细注释的代码
#include <iostream>
#include <cstring>
using namespace std;const int N = 5;
char g[N][N], bg[N][N];// 翻转灯的状态
void flip(char& x) {x = (x == '0') ? '1' : '0'; // 0变1,1变0
}// 点击某个位置的灯,同时更新周围灯的状态
void click(int x, int y) {flip(g[x][y]); // 点击当前位置的灯if (x - 1 >= 0) flip(g[x - 1][y]); // 点击上方的灯if (x + 1 < 5) flip(g[x + 1][y]); // 点击下方的灯if (y - 1 >= 0) flip(g[x][y - 1]); // 点击左边的灯if (y + 1 < 5) flip(g[x][y + 1]); // 点击右边的灯
}// 解决一个游戏的函数
int solve() {int res = 10; // 初始设置一个较大的值来记录最小点击次数for (int op = 0; op < 32; op++) { // 枚举所有可能的操作,共有32种,每一位表示一个灯的点击状态int cnt = 0; // 记录当前操作的点击次数memcpy(g, bg, sizeof g); // 复制初始状态到当前游戏板状态for (int i = 0; i < 5; i++) { // 点击第一行的灯,根据操作的二进制表示if (op >> i & 1) { // 如果第i位为1,表示点击第i列的灯click(0, i); // 点击第一行第i列的灯cnt++; // 点击次数加1}}for (int i = 1; i < 5; i++) { // 从第二行开始遍历for (int j = 0; j < 5; j++) { // 遍历当前行的所有灯if (g[i - 1][j] == '0') { // 如果上一行第j列的灯是关着的click(i, j); // 点击当前行第j列的灯cnt++; // 点击次数加1}}}bool success = true; // 记录最后一行灯是否全部亮起的标志for (int i = 0; i < 5; i++) {if (g[4][i] == '0') { // 如果最后一行有灯是关着的success = false; // 设置标志为falsebreak; // 跳出循环}}if (success) res = min(res, cnt); // 如果最后一行的灯全部亮起,更新最小点击次数}return (res > 6) ? -1 : res; // 返回满足条件的最小点击次数,如果无法在6次点击以内使所有灯变亮,则返回-1
}int main() {int T;cin >> T; // 读取数据组数while (T--) { // 处理每一组数据for (int i = 0; i < 5; i++) {cin >> bg[i]; // 读取游戏板的初始状态}int result = solve(); // 使用solve()函数解决游戏,得到结果cout << result << endl; // 输出结果}return 0;
}
相关文章:

搜索综合训练
搜索综合训练 选数详细注释的代码 小木棍详细注释的代码 费解的开关详细注释的代码 选数 详细注释的代码 #include <iostream> #include <vector>using namespace std;// 判断一个数是否为素数 bool isPrime(int num) {if (num < 1)return false;// 判断从2到s…...
sherpa-onnx实现离线语音识别【语音助手】)
snowboy+新一代kaldi(k2-fsa)sherpa-onnx实现离线语音识别【语音助手】
背景 本系列主要目标初步完成一款智能音箱的基础功能,包括语音唤醒、语音识别(语音转文字)、处理用户请求(比如查天气等,主要通过rasa自己定义意图实现)、语音合成(文字转语音)功能。 语音识别、语音合成采用离线方式实现。 语…...
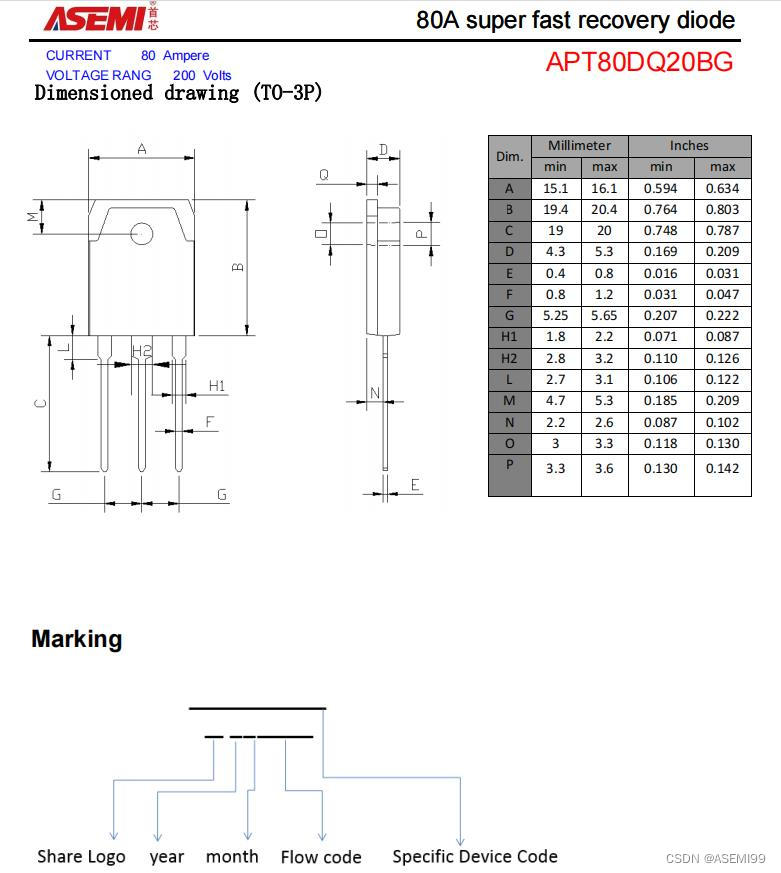
APT80DQ20BG-ASEMI快恢复二极管80A 200V
编辑:ll APT80DQ20BG-ASEMI快恢复二极管80A 200V 型号:APT80DQ20BG 品牌:ASEMI 芯片个数:双芯片 封装:TO-3P 恢复时间:≤50ns 工作温度:-55C~150C 浪涌电流:600A*2 正向电流…...

Go的任务调度单元与并发编程
摘要:本文由葡萄城技术团队于CSDN原创并首发。转载请注明出处:葡萄城官网,葡萄城为开发者提供专业的开发工具、解决方案和服务,赋能开发者。 前言 本文主要介绍Go语言、进程、线程、协程的出现背景原因以及Go 语言如何解决协程的…...

PDFbox教程_编程入门自学教程_菜鸟教程-免费教程分享
教程简介 PDFBox是一个开源Java库,支持PDF文档的开发和转换.使用此库,您可以开发用于创建,转换和操作PDF文档的Java程序.除此之外,PDFBox还包括一个命令行实用程序,用于使用可用的PDF对PDF执行各种操作Jar文件. PDFB…...

Node.js-模块化理解及基本使用
模块化的定义 讲一个复杂的程序文件按照一定的规则拆分成多个独立的小文件,这些小文件就是小模块,这就是模块化。 每个小模块内部的数据是私有的,可以暴露内部数据给外部其他模块使用。 模块化优点 减少命名的冲突提高复用性提高可维护性按需…...

arguments 和 剩余参数
加油 !! 💕 文章目录 前言一、arguments二、arguments转成array三、箭头函数不绑定arguments四、剩余参数 ... 前言 其实在es6之后不推荐使用 arguments , 建议使用剩余参数 一、arguments arguments 是一个 对应于 传递给函数的参数 的 类数…...
)
【BASH】回顾与知识点梳理(十二)
【BASH】回顾与知识点梳理 十二 十二. Linux 文件与目录管理12.1 目录与路径相对路径与绝对路径相对路径的用途绝对路径的用途 12.2 目录的相关操作cd (change directory, 变换目录)pwd (Print Working Directory, 显示目前所在的目录)mkdir (make directory, 建立新目录)rmdir…...
本地构建包含java和maven的镜像
目录 1.前提条件 2.下载 2.1.创建Dockerfile 3.构建镜像 参考文章 1.前提条件 本地环境需要的系统和软件 win10 Docker Desktop Powershell 图1 Win10安装Docker后,直接在Powershell使用Docker命令 有些Developer不习惯win10系统,却想要使用Lin…...

Programming abstractions in C阅读笔记:p76-p83
《Programming Abstractions In C》学习第42天,p76-p73总结。 一、技术总结 1.数组和指针 在C语言中,数组和指针非常相似,相似到必须将它们同时考虑,当看到数组就应该想到指针,当看到指针就应该想到数组。示例…...
|neo4j Failed authentication attempt for ‘meter‘ from 127.0.0.1)
已解决(三个问题)|neo4j Failed authentication attempt for ‘meter‘ from 127.0.0.1
问题1 py2neo.errors.ConnectionUnavailable: Connection has been closed 问题2 neo4j Failed authentication attempt for ‘meter’ from 127.0.0.1 问题3 py2neo.errors,ClientError: [Security.Unauthorized] Invalid username or password. 作者:xiao黄 博客地址:http…...
neo4j查询语言Cypher详解(二)--Pattern和类型
Patterns 图形模式匹配是Cypher的核心。它是一种用于通过应用声明性模式从图中导航、描述和提取数据的机制。在MATCH子句中,可以使用图模式定义要搜索的数据和要返回的数据。图模式匹配也可以在不使用MATCH子句的情况下在EXISTS、COUNT和COLLECT子查询中使用。 图…...

动态规划(用空间换时间的算法)原理逻辑代码超详细!参考自《算法导论》
动态规划(用空间换时间的算法)-实例说明和用法详解 动态规划(DP)思想实例说明钢条切割问题矩阵链乘法问题 应用满足的条件和场景 本篇博客以《算法导论》第15章动态规划算法为本背景,大量引用书中内容和实例࿰…...

Jmeter添加cookie的两种方式
jmeter中添加cookie可以通过配置HTTP Cookie Manager,也可以通过HTTP Header Manager,因为cookie是放在头文件里发送的。 实例:博客园点击添加新随笔 https://i.cnblogs.com/EditPosts.aspx?opt1 如果未登录,跳转登录页…...
【ArcGIS Pro二次开发】(58):数据的本地化存储
在做村规工具的过程中,需要设置一些参数,比如说导图的DPI,需要导出的图名等等。 每次导图前都需要设置参数,虽然有默认值,但还是需要不时的修改。 在使用的过程中,可能会有一些常用的参数,希望…...

React配置代理服务器的5种方法
五种方法的介绍 以下是五种在React项目中配置代理服务器的方法的使用场景和优缺点: 1. 使用 http-proxy-middleware 中间件: 使用场景:适用于大多数React项目,简单易用。优点:配置简单,易于理解和维护。…...

树莓派:5.jar程序自启运行
搞了好长时间才搞定,普通的jar文件好启动。神奇的在于在ssh里启动GPIO可以操作,但是自启动GPIO不能控制。第二天才想明白估计是GPIO的操作权限比较高,一试果然如此,特此记录。 1、copy程序文件和sh文件在Public下 piraspberrypi…...

Vivado中SmartConnect和InterConnect的区别
前言:本文章为FPGA问答系列,我们会定期整理FPGA交流群(包括其他FPGA博主的群)里面有价值的问题,并汇总成文章,如果问题多的话就每周整理一期,如果问题少就每两周整理一期,一方面是希…...

了解HTTP代理日志:解读请求流量和响应信息
嗨,爬虫程序员们!你们是否在了解爬虫发送的请求流量和接收的响应信息上有过困扰?今天,我们一起来了解一下。 首先,我们需要理解HTTP代理日志的基本结构和内容。HTTP代理日志是对爬虫发送的请求和接收的响应进行记录的文…...

排序-堆排序
给你一个整数数组 nums,请你将该数组升序排列。 输入:nums [5,2,3,1] 输出:[1,2,3,5] 输入:nums [5,1,1,2,0,0] 输出:[0,0,1,1,2,5] 思路直接看我录制的视频吧 算法-堆排序_哔哩哔哩_bilibili 实现代码如下所示&…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...
