2019蓝桥杯真题平方序列(填空题) C语言/C++
题目描述
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
小明想找到两个正整数 X 和 Y,满足2019<X<Y;2019^2, X^2, Y^2组成等差数列。
请你求出在所有可能的解中,X+Y 的最小值是多少?
运行限制
最大运行时间:1s
最大运行内存: 128M
所需变量
int a = 2019;//由于是填空题,我直接把2019赋值给a了
int x = 2020;//这是为了满足条件x比a大
int y = 2021;//满足条件y大于x也大于a
首先我们拿到这个题的时候,我们的第一感觉就是很难,而却算法所耗费的时间肯定很大,因为我们要不断的去尝试x和y同时满足!
那么我们的第一想法就是每次让x+1,然后也让y+1!仔细想想是不对的,这样肯定会不满足时间要求,时间复杂度太高了
因此我们想到一个更好的方法!
首先我们分析题目,我们要找的数要满足等差数列!
对于等差数列的性质就是第二个数(即x)与第一个数(a)的差值等于第三个数(y)与第二个数(x)的差值
用数学公式表示就是y*y-x*x = x*x - a*a
得到这个后,我们就可以明白了,当x+1,y不用直接+1,而是可以直接取向上取整(根号(2*x*x-a*a))
代码如下:
if(y < sqrt(2*x*x-2019*2019)){y = ceil(sqrt(2*x*x-2019*2019));}
如果对于y变化过大,那么当我们需要调整x的时候,我们就是(向上取整(开根号((y*y+a*a)/2)))
代码如下:
if(y > sqrt(2*x*x-2019*2019)){x = ceil(sqrt((y*y+2019*2019)/2));}
当然啦,终止条件就是满足等差数列性质,即y*y ==(2*x*x-2019*2019)我们就跳出循环!
该算法本人认为比较优,如果有更好的想法,欢迎q我!
完整代码如下(编译器是dev,语言是C语言):
#include <iostream>
#include<math.h>
using namespace std;
int main()
{int a = 2019,x = 2020,y = 2021;while(true){if(y*y ==(2*x*x-2019*2019)){break;}else if(y > sqrt(2*x*x-2019*2019)){x = ceil(sqrt((y*y+2019*2019)/2));}else if(y < sqrt(2*x*x-2019*2019)){y = ceil(sqrt(2*x*x-2019*2019));}}cout<<x+y<<endl;return 0;
}

相关文章:

2019蓝桥杯真题平方序列(填空题) C语言/C++
题目描述 本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。 小明想找到两个正整数 X 和 Y,满足2019<X<Y;2019^2, X^2, Y^2组成等差数列。 请你求出在所有可能的解中,XY 的最小值是多少?…...
vue中,给一个URL地址,利用FileSaver.js插件下载文件到本地
①首先下载 FileSaver.js 插件 npm install file-saver --save ②在需要的.vue页面引入 import { saveAs } from file-saver 在HTML中引入 <script src"https://cdn.bootcdn.net/ajax/libs/FileSaver.js/2.0.5/FileSaver.min.js"></script> //Fil…...
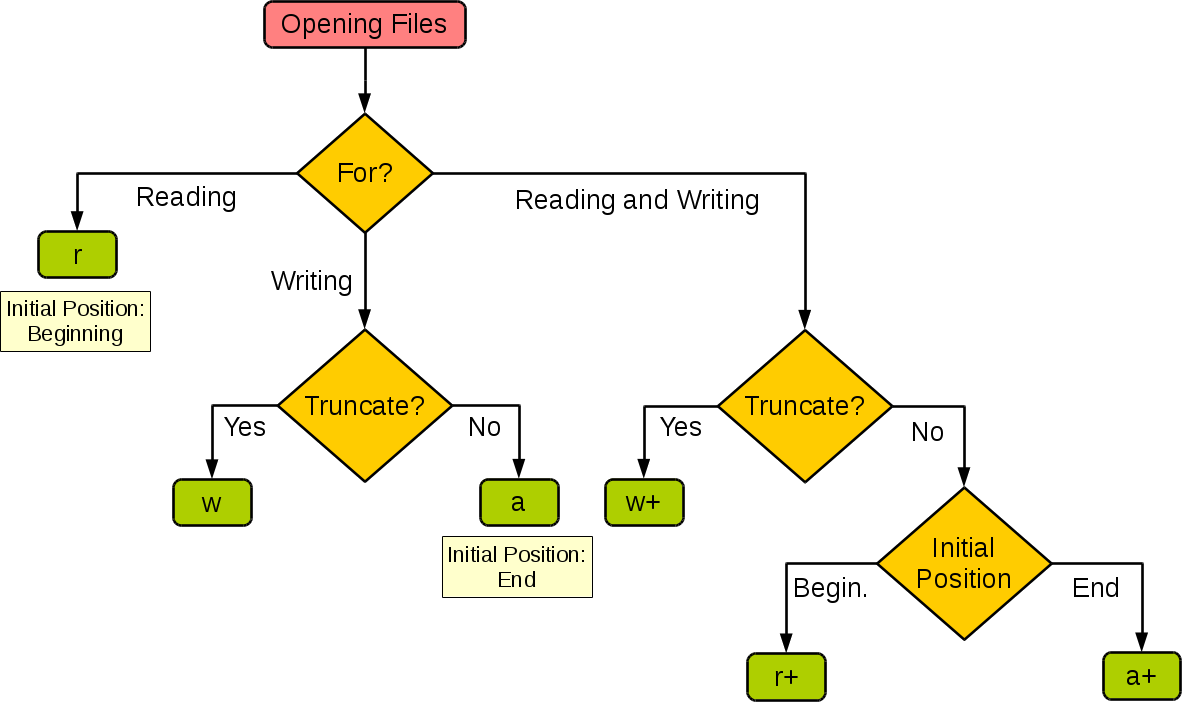
从0开始学python -34
Python3 输入和输出-2 读和写文件 open() 将会返回一个 file 对象,基本语法格式如下: open(filename, mode)filename:包含了你要访问的文件名称的字符串值。mode:决定了打开文件的模式:只读,写入,追加等。…...

瑞典军事研究:从认知心理学的视角探讨军事创新进程
来源:Military Innovation as the Result of Mental Models of Technology 《摘要》 政治紧张局势的加剧和技术发展的进步促使Scandinavian 国家(斯堪的纳维亚半岛,欧洲最大的半岛,有挪威、瑞典两国以及芬兰北端的一小部分。&am…...

【MySQL进阶-08】深入理解innodb存储格式,双写机制,buffer pool底层结构和淘汰策略
MySql系列整体栏目 内容链接地址【一】深入理解mysql索引本质https://blog.csdn.net/zhenghuishengq/article/details/121027025【二】深入理解mysql索引优化以及explain关键字https://blog.csdn.net/zhenghuishengq/article/details/124552080【三】深入理解mysql的索引分类&a…...

5. AOP
一、如何定义一个MethodHandler? 1.Controller注解修饰的类 1.注册成Spring Bean 2.表示它是一个SpringMVC下的Controller 2.在这个类下的方法中,只要被RequestMapping修饰&&方法的形参符合规定(需要看文档) 方法的返回值符合规定…...

ubuntu上尝试libpqxx库链接人大金仓
ubuntu上尝试libpqxx库链接人大金仓 C的项目让使用国产数据库 运维给架了一个人大金仓数据库, Kingbase 8 是基于 PostgreSQL 9.6 做的, 尝试直接使用libpqxx链接数据库。 文章目录ubuntu上尝试libpqxx库链接人大金仓第一步 搭建libpqxx开发环境搜索lib…...
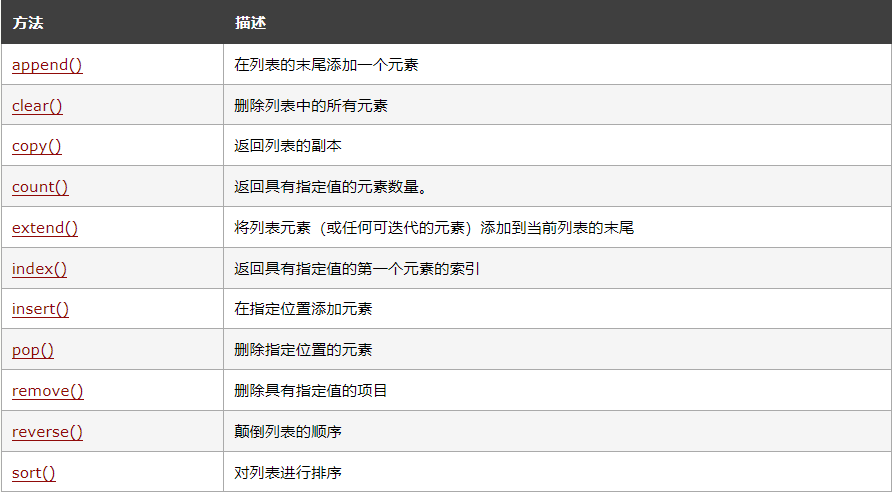
【Python入门第十二天】Python 列表
Python 集合(数组) Python 编程语言中有四种集合数据类型: 列表(List)是一种有序和可更改的集合。允许重复的成员。元组(Tuple)是一种有序且不可更改的集合。允许重复的成员。集合(…...

Android 异步操作库 RxJava
RxJava概述 RxJava 是一种响应式编程,来创建基于事件的异步操作库。基于事件流的链式调用、逻辑清晰简洁。 RxJava 我的理解是将事件从起点(上游)流向终点(下游),中间有很多卡片对数据进操作并传递&#x…...
等级考试试卷(六级)解析)
2021-12-05青少年软件编程(C语言)等级考试试卷(六级)解析
2021-12-05青少年软件编程(C语言)等级考试试卷(六级)解析T1. 电话号码 给你一些电话号码,请判断它们是否是一致的,即是否有某个电话是另一个电话的前缀。比如: Emergency 911 Alice 97 625 999 Bob 91 12 54 26 在这个例子中,我们不可能拨通Bob的电话,因为Emergency的…...
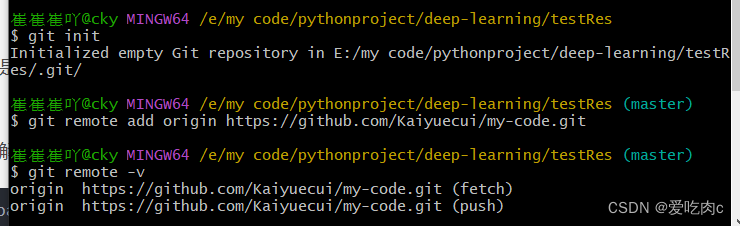
github 使用
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录一、git与github二、出错的地方1.GitHub没有css样式2、git clone出现错误3、明明创建了responsibility 但git 不显示一、git与github 这个博客写的很好!…...
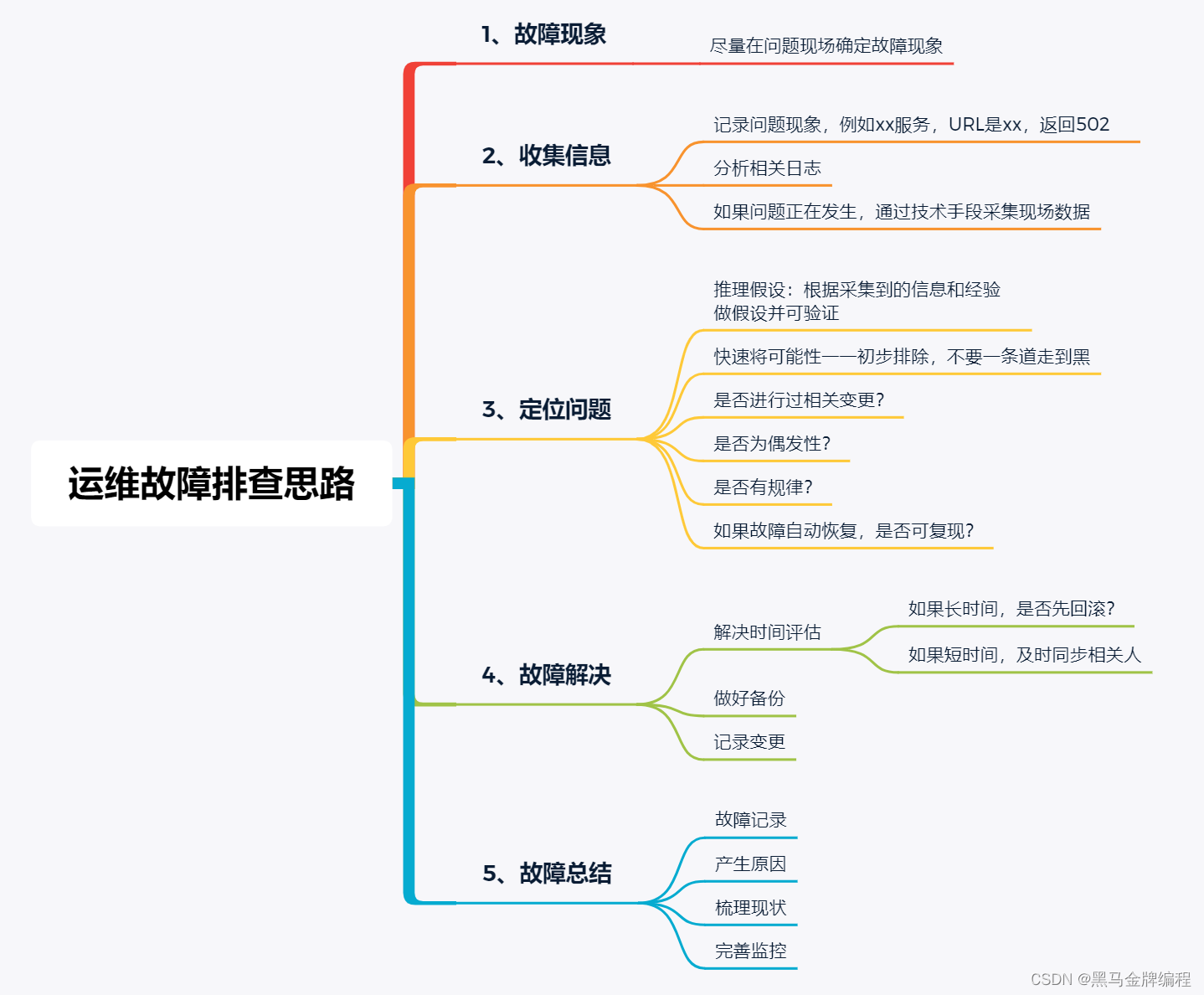
Kubernetes集群维护—备份恢复与升级
Etcd数据库备份与恢复 需要先安装etcd备份工具yum install etcd -y按不同安装方式执行不同备份与恢复kubeadm部署方式: 备份:ETCDCTL_API3 etcdctl snapshot save snap.db --endpointshttps://127.0.0.1:2379 --cacert/etc/kubernetes/pki/etcd/ca.cr…...
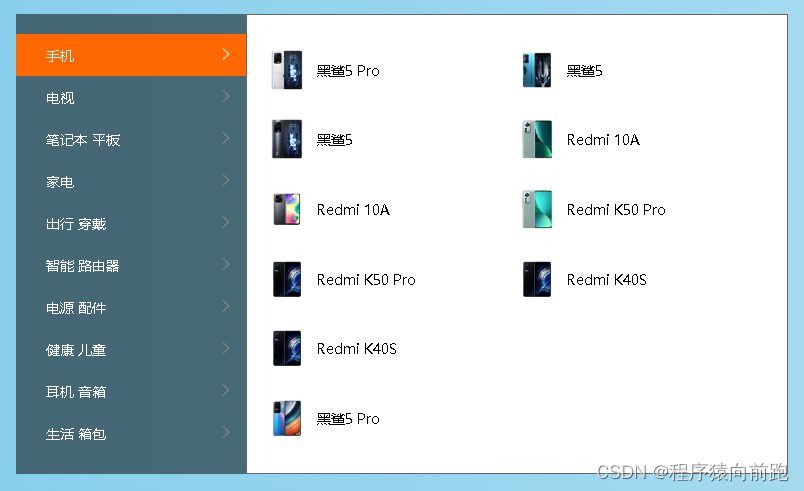
前端开发常用案例(二)
这里写目录标题1.loding加载动画2.全屏加载动画效果3.吃豆豆4.鼠标悬停3D翻转效果5.3D旋转木马效果6.flex弹性布局-酷狗音乐播放列表flex弹性布局-今日头条首页热门视频栏grid网格布局-360图片展示小米商城左侧二级菜单1.loding加载动画 代码如下: <!DOCTYPE h…...

基于springboot+vue的儿科保健计划免疫系统
基于springbootvue的儿科保健计划免疫系统 ✌全网粉丝20W,csdn特邀作者、博客专家、CSDN新星计划导师、java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取项目下载方式🍅 一、项目背…...

1.两数之和
难度简单给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。你可以按任意顺序…...

字符串匹配 - 模式预处理:KMP 算法(Knuth-Morris-Pratt)
Knuth-Morris-Pratt算法(简称KMP)是最常用的字符串匹配算法之一。算法简介如下算法解释主要来源于这里,但是通常很难阅读完全,我推荐你直接进入下一节 图例解释部分。我们来观察一下朴素的字符串匹配算法的操作过程。如下图&#…...
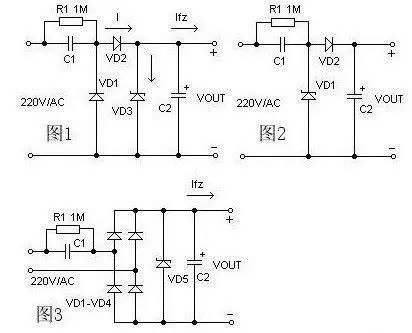
工程师手册:电源设计中的电容选用规则
摘要 电源往往是我们在电路设计过程中最容易忽略的环节。作为一款优秀的设计,电源设计应当是很重要的,它很大程度影响了整个系统的性能和成本。电源设计中的电容使用,往往又是电源设计中最容易被忽略的地方。一、电源设计中电容的工作原理 在…...

【安全开发】专栏文章汇总
安全开发–1–TCP和UDP网络编程 安全开发–2–嗅探邮箱协议口令 安全开发–3–Python实现ARP缓存投毒 安全开发–4–SSH通信工具开发 安全开发–5–编写简单的netcat工具 安全开发–6–一个简单的TCP代理工具开发 安全开发–7–SSH隧道工具开发 安全开发–8–Python实现流量数据…...

视频监控流程图4
<html> <head> <meta http-equiv"Content-Type" content"text/html; charsetUTF-8"/> <link rel"stylesheet" type"text/css" href"visio.css"/> <title> 视频监控流程图 </title> <…...
)
「JVM 编译优化」Java 语法糖(泛型、自动装箱/拆箱、条件编译)
「JVM 编译优化」Java 语法糖(泛型、自动装箱/拆箱、条件编译) 语法糖可以看做事前端编译期的一些小把戏;虽不会提供实质性的功能改进,但它们或能提高效率,或能提升语法的严谨性,或能减少编码出错的机会&a…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...
