字符串匹配 - 模式预处理:KMP 算法(Knuth-Morris-Pratt)
Knuth-Morris-Pratt算法(简称KMP)是最常用的字符串匹配算法之一。
算法简介
如下算法解释主要来源于这里,但是通常很难阅读完全,我推荐你直接进入下一节 图例解释部分。
我们来观察一下朴素的字符串匹配算法的操作过程。如下图(a)中所描述,在模式 P = ababaca 和文本 T 的匹配过程中,模板的一个特定位移 s,q = 5 个字符已经匹配成功,但模式 P 的第 6 个字符不能与相应的文本字符匹配。

此时,q 个字符已经匹配成功的信息确定了相应的文本字符,而知道这 q 个文本字符,就使我们能够立即确定某些位移是非法的。例如上图(a)中,我们可以判断位移 s+1 是非法的,因为模式 P 的第一个字符 a 将与模式的第二个字符 b 匹配的文本字符进行匹配,显然是不匹配的。而图(b)中则显示了位移 s’ = s+2 处,使模式 P 的前三个字符和相应的三个文本字符对齐后必定会匹配。KMP 算法的基本思路就是设法利用这些已知信息,不要把 "搜索位置" 移回已经比较过的位置,而是继续把它向后面移,这样就提高了匹配效率。
The basic idea behind KMP’s algorithm is: whenever we detect a mismatch (after some matches), we already know some of the characters in the text (since they matched the pattern characters prior to the mismatch). We take advantage of this information to avoid matching the characters that we know will anyway match.
已知模式 P[1..q] 与文本 T[s+1..s+q] 匹配,那么满足 P[1..k] = T[s’+1..s’+k] 其中 s’+k = s+q 的最小位移 s’ > s 是多少?这样的位移 s’ 是大于 s 的但未必非法的第一个位移,因为已知 T[s+1..s+q] 。在最好的情况下有 s’ = s+q,因此立刻能排除掉位移 s+1, s+2 .. s+q-1。在任何情况下,对于新的位移 s’,无需把 P 的前 k 个字符与 T 中相应的字符进行比较,因为它们肯定匹配。
可以用模式 P 与其自身进行比较,以预先计算出这些必要的信息。例如上图(c)中所示,由于 T[s’+1..s’+k] 是文本中已经知道的部分,所以它是字符串 Pq 的一个后缀。
此处我们引入模式的前缀函数 π(Pai),π 包含有模式与其自身的位移进行匹配的信息。这些信息可用于避免在朴素的字符串匹配算法中,对无用位移进行测试。
π[q]= max {k : k < q and Pk ⊐ Pq}π[q] 代表当前字符之前的字符串中,最长的共同前缀后缀的长度。(π[q] is the length of the longest prefix of P that is a proper suffix of Pq.)
下图给出了关于模式 P = ababababca 的完整前缀函数 π,可称为部分匹配表(Partial Match Table)。

计算过程:
π[1] = 0,a 仅一个字符,前缀和后缀为空集,共有元素最大长度为 0;
π[2] = 0,ab 的前缀 a,后缀 b,不匹配,共有元素最大长度为 0;
π[3] = 1,aba,前缀 a ab,后缀 ba a,共有元素最大长度为 1;
π[4] = 2,abab,前缀 a ab aba,后缀 bab ab b,共有元素最大长度为 2;
π[5] = 3,ababa,前缀 a ab aba abab,后缀 baba aba ba a,共有元素最大长度为 3;
π[6] = 4,ababab,前缀 a ab aba abab ababa,后缀 babab abab bab ab b,共有元素最大长度为 4;
π[7] = 5,abababa,前缀 a ab aba abab ababa ababab,后缀 bababa ababa baba aba ba a,共有元素最大长度为 5;
π[8] = 6,abababab,前缀 .. ababab ..,后缀 .. ababab ..,共有元素最大长度为 6;
π[9] = 0,ababababc,前缀和后缀不匹配,共有元素最大长度为 0;
π[10] = 1,ababababca,前缀 .. a ..,后缀 .. a ..,共有元素最大长度为 1;
KMP 算法 KMP-MATCHER 中通过调用 COMPUTE-PREFIX-FUNCTION 函数来计算部分匹配表。
KMP-MATCHER(T, P)
n ← length[T]
m ← length[P]
π ← COMPUTE-PREFIX-FUNCTION(P)
q ← 0 //Number of characters matched.
for i ← 1 to n //Scan the text from left to right.do while q > 0 and P[q + 1] ≠ T[i]do q ← π[q] //Next character does not match.if P[q + 1] = T[i]then q ← q + 1 //Next character matches.if q = m //Is all of P matched?then print "Pattern occurs with shift" i - mq ← π[q] //Look for the next match.COMPUTE-PREFIX-FUNCTION(P)
m ← length[P]
π[1] ← 0
k ← 0
for q ← 2 to mdo while k > 0 and P[k + 1] ≠ P[q]do k ← π[k]if P[k + 1] = P[q]then k ← k + 1π[q] ← k
return π预处理过程 COMPUTE-PREFIX-FUNCTION 的运行时间为 Θ(m),KMP-MATCHER 的匹配时间为 Θ(n)。
相比较于 NAIVE-STRING-MATCHER,KMP-MATCHER 的主要优化点就是在当确定字符不匹配时对于 pattern 的位移。
NAIVE-STRING-MATCHER 的位移效果是:文本向后移一位,模式从头开始。
s = s - j +1;j =0;KMP-MATCHER 首先对模式做了获取共同前缀后缀最大长度的预处理操作,位移过程是先将模式向后移 partial_match_length - table[partial_match_length - 1],然后再判断是否匹配。这样通过对已匹配字符串的已知信息的利用,可以有效节省比较数量。
if(j !=0)j = lps[j -1];elses++;下面描述了当发现字符 j 与 c 不匹配时的位移效果。
// partial_match_length - table[partial_match_length - 1]rrababababjjjjjiiooorababababcauuu||||||||-ababababca// 8-6=2rrababababjjjjjiiooorababababcauuuxx||||||-ababababca// 6-4=2rrababababjjjjjiiooorababababcauuuxx||||-ababababca// 4-2=2rrababababjjjjjiiooorababababcauuuxx||-ababababca// 2-0=2rrababababjjjjjiiooorababababcauuuxx-ababababca综上可知,KMP 算法的主要特点是:
需要对模式字符串做预处理;
预处理阶段需要额外的 O(m) 空间和复杂度;
匹配阶段与字符集的大小无关;
匹配阶段至多执行 2n - 1 次字符比较;
对模式中字符的比较顺序时从左到右;
算法图例
如下是阮一峰根据Jake Boxer的文章总结的图例。
下面,我用自己的语言,试图写一篇比较好懂的KMP算法解释。

首先,字符串"BBC ABCDAB ABCDABCDABDE"的第一个字符与搜索词"ABCDABD"的第一个字符,进行比较。因为B与A不匹配,所以搜索词后移一位。

因为B与A不匹配,搜索词再往后移。

就这样,直到字符串有一个字符,与搜索词的第一个字符相同为止。

接着比较字符串和搜索词的下一个字符,还是相同。

直到字符串有一个字符,与搜索词对应的字符不相同为止。

这时,最自然的反应是,将搜索词整个后移一位,再从头逐个比较。这样做虽然可行,但是效率很差,因为你要把"搜索位置"移到已经比较过的位置,重比一遍。

一个基本事实是,当空格与D不匹配时,你其实知道前面六个字符是"ABCDAB"。KMP算法的想法是,设法利用这个已知信息,不要把"搜索位置"移回已经比较过的位置,继续把它向后移,这样就提高了效率。

怎么做到这一点呢?可以针对搜索词,算出一张《部分匹配表》(Partial Match Table)。这张表是如何产生的,后面再介绍,这里只要会用就可以了。

已知空格与D不匹配时,前面六个字符"ABCDAB"是匹配的。查表可知,最后一个匹配字符B对应的"部分匹配值"为2,因此按照下面的公式算出向后移动的位数:
移动位数 = 已匹配的字符数 - 对应的部分匹配值
因为 6 - 2 等于4,所以将搜索词向后移动4位。

因为空格与C不匹配,搜索词还要继续往后移。这时,已匹配的字符数为2("AB"),对应的"部分匹配值"为0。所以,移动位数 = 2 - 0,结果为 2,于是将搜索词向后移2位。

因为空格与A不匹配,继续后移一位。

逐位比较,直到发现C与D不匹配。于是,移动位数 = 6 - 2,继续将搜索词向后移动4位。

逐位比较,直到搜索词的最后一位,发现完全匹配,于是搜索完成。如果还要继续搜索(即找出全部匹配),移动位数 = 7 - 0,再将搜索词向后移动7位,这里就不再重复了。

下面介绍《部分匹配表》是如何产生的。
首先,要了解两个概念:"前缀"和"后缀"。 "前缀"指除了最后一个字符以外,一个字符串的全部头部组合;"后缀"指除了第一个字符以外,一个字符串的全部尾部组合。

"部分匹配值"就是"前缀"和"后缀"的最长的共有元素的长度。以"ABCDABD"为例,
- "A"的前缀和后缀都为空集,共有元素的长度为0;- "AB"的前缀为[A],后缀为[B],共有元素的长度为0;- "ABC"的前缀为[A,AB],后缀为[BC,C],共有元素的长度0;- "ABCD"的前缀为[A,AB,ABC],后缀为[BCD,CD,D],共有元素的长度为0;- "ABCDA"的前缀为[A,AB,ABC,ABCD],后缀为[BCDA,CDA,DA,A],共有元素为"A",长度为1;- "ABCDAB"的前缀为[A,AB,ABC,ABCD,ABCDA],后缀为[BCDAB,CDAB,DAB,AB,B],共有元素为"AB",长度为2;- "ABCDABD"的前缀为[A,AB,ABC,ABCD,ABCDA,ABCDAB],后缀为[BCDABD,CDABD,DABD,ABD,BD,D],共有元素的长度为0。
"部分匹配"的实质是,有时候,字符串头部和尾部会有重复。比如,"ABCDAB"之中有两个"AB",那么它的"部分匹配值"就是2("AB"的长度)。搜索词移动的时候,第一个"AB"向后移动4位(字符串长度-部分匹配值),就可以来到第二个"AB"的位置。
相关文章:

字符串匹配 - 模式预处理:KMP 算法(Knuth-Morris-Pratt)
Knuth-Morris-Pratt算法(简称KMP)是最常用的字符串匹配算法之一。算法简介如下算法解释主要来源于这里,但是通常很难阅读完全,我推荐你直接进入下一节 图例解释部分。我们来观察一下朴素的字符串匹配算法的操作过程。如下图&#…...
工程师手册:电源设计中的电容选用规则
摘要 电源往往是我们在电路设计过程中最容易忽略的环节。作为一款优秀的设计,电源设计应当是很重要的,它很大程度影响了整个系统的性能和成本。电源设计中的电容使用,往往又是电源设计中最容易被忽略的地方。一、电源设计中电容的工作原理 在…...

【安全开发】专栏文章汇总
安全开发–1–TCP和UDP网络编程 安全开发–2–嗅探邮箱协议口令 安全开发–3–Python实现ARP缓存投毒 安全开发–4–SSH通信工具开发 安全开发–5–编写简单的netcat工具 安全开发–6–一个简单的TCP代理工具开发 安全开发–7–SSH隧道工具开发 安全开发–8–Python实现流量数据…...

视频监控流程图4
<html> <head> <meta http-equiv"Content-Type" content"text/html; charsetUTF-8"/> <link rel"stylesheet" type"text/css" href"visio.css"/> <title> 视频监控流程图 </title> <…...
)
「JVM 编译优化」Java 语法糖(泛型、自动装箱/拆箱、条件编译)
「JVM 编译优化」Java 语法糖(泛型、自动装箱/拆箱、条件编译) 语法糖可以看做事前端编译期的一些小把戏;虽不会提供实质性的功能改进,但它们或能提高效率,或能提升语法的严谨性,或能减少编码出错的机会&a…...
Linux下的进程控制
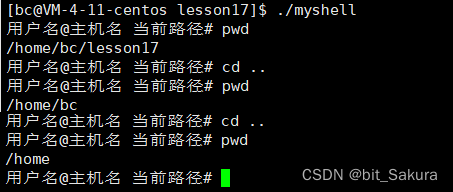
目录 退出码 终止进程 进程等待 进程程序替换 自己实现简易shell命令行 内建命令 退出码 在编写代码时main函数内部我们通常都使用return 0;结尾,以此标识正常退出。这里的return 0就是所谓的退出码,Linux下也是一样: 看这个小程序&…...
QT 文件监视系统QFileSystemWatcher监视目录的改变directoryChanged和监视文件的改变fileChanged
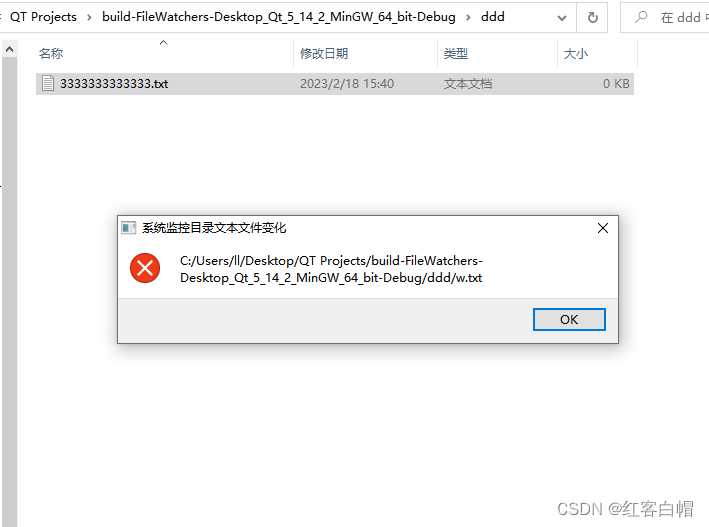
QT 文件监视系统QFileSystemWatcher监视目录的改变相关操作说明mainwindow.hmainwindow.cpp调试结果相关操作说明 添加头文件 Header: #include qmake: QT core bool QFileSystemWatcher::addPath(const QString &path)如果路径存在,则会向文件系统监视器添…...
)
Typescript基础知识(类型断言、类型别名、字符串字面量类型、枚举、交叉类型)
系列文章目录 引入一:Typescript基础引入(基础类型、元组、枚举) 引入二:Typescript面向对象引入(接口、类、多态、重写、抽象类、访问修饰符) 第一章:Typescript基础知识(Typescri…...
Windows系统扩充C盘空间系列方法总结
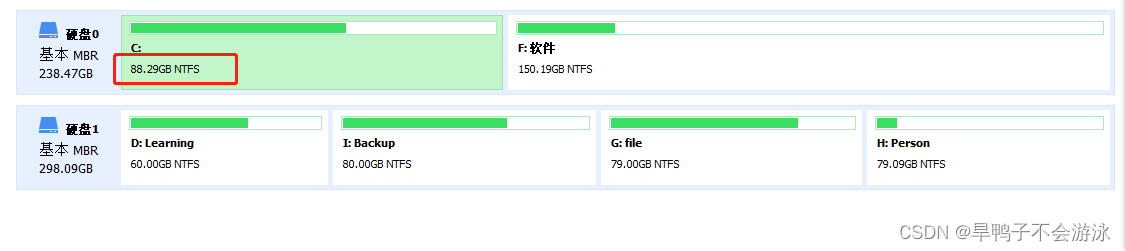
目录前言方法一 使用自带的Windows的DiskPart扩充C盘1. 打开cmd2.三步命令方法二:使用Windows系统内置磁盘管理扩展C盘方法三. 使用专业磁盘分区工具总结前言 本教程是总结Windows系统进行C盘(系统盘)扩充空间的系列方法,一般来讲…...
)
华为OD机试 - 跳格子(Python)
跳格子 题目 地上共有N个格子,你需要跳完地上所有的格子, 但是格子间是有强依赖关系的,跳完前一个格子后, 后续的格子才会被开启,格子间的依赖关系由多组steps数组给出, steps[0]表示前一个格子,steps[1]表示steps[0]可以开启的格子: 比如[0,1]表示从跳完第0个格子以后…...

Java配置文件的值注入
1.平常使用直接在变量头上加上Value就可以把配置文件的值注入进来 Value(“${environment.active}”) private String environment; 2.但是变量使用static修饰时,就不能注入进来了 Value(“${environment.active}”) private static String environment; 这是因…...

SAP 订单BOM与销售BOM的区别
订单BOM与销售BOM的区别 訂單BOM: 是實際生產時用的BOM, 在標準BOM和銷售BOM基礎上增減物料的BOM 銷售BOM: 是為特定客戶設定的BOM, 在主檔數據層次上的BOM, 在生產時是帶到訂單BOM中去的. 標準BOM: 是公司為標準生產的BOM, 在主檔數據層次上的BOM, 在生產時是帶到訂單BOM中去的…...

支付宝支付详细流程
1、二维码的生成二维码生成坐标 <!-- zxing生成二维码 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.3.3</version></dependency><dependency><groupId>co…...

TCP 的演化史-fast retransmit/recovery
工作原因要对一个 newreno 实现增加 sack 支持。尝试写了 3 天 C,同时一遍又一遍梳理 sack 标准演进。这些东西我早就了解,但涉及落地写实现,就得不断抠细节,试图写一个完备的实现。 这事有更简单的方法。根本没必要完全实现 RFC…...
CSS基础选择器,你认识多少?
前言在上一文初识CSS中,我们了解到了其格式:选择器{ }在初步尝试使用时,我们笼统的直接输入了p { }以选择p标签来对其操作,而这一章节里,我们再进一步探索有关基础选择器的相关内容,理解选择器的作用。选择…...

ChatGPT入门案例|商务智能对话客服(三)
本篇介绍智能客服的基本功能架构和基本概念,并利用对话流技术构建商务智能应用。 01、商务智能客服功能结构 互联网的发展已经深入到社会的各个方面,智能化发展已经成为社会发展的大趋势。在大数据和互联网时代,企业和组织愈加重视客户沟通…...
Matlab 最小二乘法拟合平面(SVD)
文章目录 一、简介1.1最小二乘法拟合平面1.2 SVD角度二、实现代码三、实现效果参考资料一、简介 1.1最小二乘法拟合平面 之前我们使用过最为经典的方式对平面进行了最小二乘拟合(点云最小二乘法拟合平面),其推导过程如下所示: 仔细观察一下可以发现...

AtCoder Regular Contest 126 D题题解
思路 首先我们看看假设选中 mmm 个数后的答案。 我们首先现将 mmm 个数移动到一起,在将他们重新排序。 我们知道,mmm 个数移在一起时,当位于中间的那个数不动时交换次数最少,于是可以列出式子(cic_ici 是点 iii 的…...

Android R WiFi热点流程浅析
Android R WiFi热点流程浅析 Android上的WiFi SoftAp功能是用户常用的功能之一,它能让我们分享手机的网络给其他设备使用。 那Android系统是如何实现SoftAp的呢,这里在FWK层面做一个简要的流程分析,供自己记录和大家参考。 以Android R版本为…...
【C++进阶】二、多态详解(总)
目录 一、多态的概念 二、多态的定义及实现 2.1 多态的构成条件 2.2 虚函数 2.3 虚函数的重写 2.4 虚函数重写的两个例外 2.4.1 协变 2.4.2 析构函数的重写 2.5 C11 override 和 final 2.5.1 final 2.5.2 override 2.6 重载、覆盖(重写)、隐藏(重定义)的对比 三、…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...
