(杭电多校)2023“钉耙编程”中国大学生算法设计超级联赛(6)
1001 Count
当k在区间(1+n)/2的左边时,如图,[1,k]和[n-k+1,n]完全相同,所以就m^(n-k)
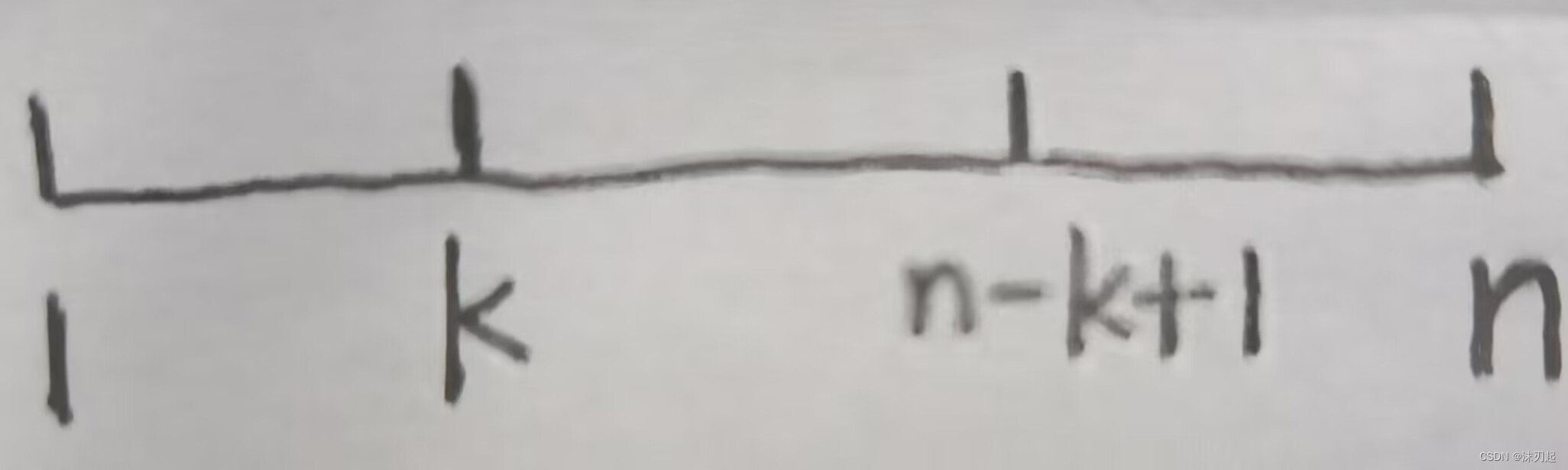
当k在区间(1+n)/2的右边时,如图,[1,n-k+1]和[k,n]完全相同,所以也是m^(n-k)
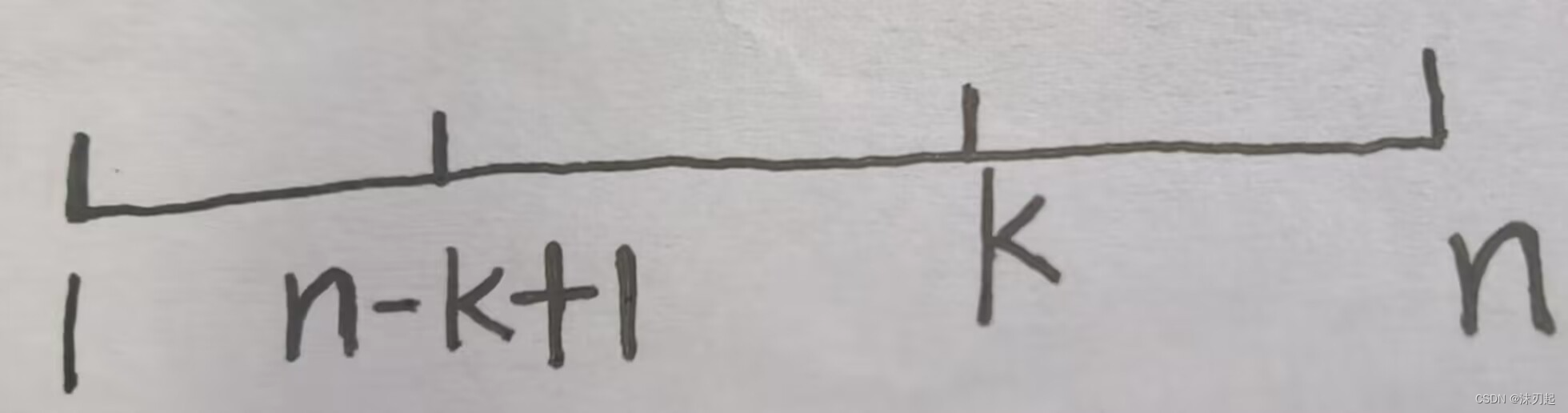
别忘了特判,当k等于n时,n-k为0,然后a1=a1,a2=a2,..an=an,所以没什么限制,那么就是m^n
AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<cstdio>
#define endl '\n'
//#define int long long
using namespace std;
typedef long long ll;
const int mod=998244353;
ll n,m,k;
ll qmi(ll a,ll k){ll res=1;while(k){if(k&1) res=res*a%mod;a=a*a%mod;k>>=1;}return res;
}
void solve() {cin>>n>>m>>k;ll res;if(n==k) res=qmi(m%mod,n)%mod;//m范围过大,可达1e18,取个模防止快速幂时爆long longelse res=qmi(m%mod,n-k)%mod;//m可以取模是因为快速幂本就是乘法运算,乘法运算完全可以一边运算一边取模cout<<res<<endl;
}
int main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t=1;cin>>t;while(t--)solve();return 0;
}参考2023杭电暑假多校6 题解 1 2 6 10 | JorbanS_JorbanS的博客-CSDN博客
1002 Pair Sum and Perfect Square
树状数组
AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
#include<cstdio>
#define endl '\n'
//#define int long long
using namespace std;
typedef long long ll;
typedef pair<int,int>PII;
const int N=1e5+10,M=450;
int p[N],pos[N];
int tr[N];
int sqr[M];
int n,q;
//树状数组
int lowbit(int x){return x & -x;
}
int sum(int x){int res=0;for(int i=x;i;i-=lowbit(i)) res+=tr[i];return res;
}
void add(int x,int c){for(int i=x;i<=n;i+=lowbit(i)) tr[i]+=c;
}
void solve() {cin>>n;memset(tr,0,sizeof tr);for(int i=1;i<=n;i++) cin>>p[i],pos[p[i]]=i;//pos记录值为p[i]的下标int m=0;for(int i=1;i*i<=2*n-1;i++) sqr[m++]=i*i;//将所有可能用到的平方数从小到大全部都记录在sqr数组中cin>>q;vector<vector<PII>>s(n+1);for(int i=0;i<q;i++){int l,r;cin>>l>>r;s[r].push_back({i,l});//右端点为r,然后将第几次询问的编号以及左端点放进去}int res=0;vector<int>ans(q+1);//枚举i从1到n,i作为右端点的编号for(int i=1;i<=n;i++){//从小到大枚举所有平方数,j为编号,sqr[j]即为平方数for(int j=0;j<m;j++){if(p[i]>=sqr[j]) continue;//如果p[i]已经大于等于该平方数了,那么说明该平方数太小了,那么就continue,继续枚举下一个平方数if(sqr[j]-p[i]>n) break;//sqr[j]即为平方数,p[i]即为右端点i的所对应的值,sqr[j]-p[i]即为左端点对应的值,如果大于n,说明该平方数太大了,那么直接break,后面平方数更大,就不用枚举了if(pos[sqr[j]-p[i]]<i) add(pos[sqr[j]-p[i]],1),res++;//如果左端点的下标小于右端点的下标i,那么就是可行的,那么以pos[sqr[j]-p[i]]为左端点的位置上个数+1,res记录有几对可行}//以i为右端点,枚举每一次询问的编号,以及询问区间[l,i],每一次遍历到的编号都是唯一的,res表示枚举到当前所有满足条件的对数,用res减去sum(l-1)算出的就是[l,i]区间里面所有满足条件的对数//首先右端点i是从小到大依次枚举的,然后前面的枚举过的右端点肯定是在i前面的,然后我们需要保证左端点要大于等于l,所以减去sum(l-1)即左端点小于等于l-1的满足条件的对数for(auto [id,l]:s[i]) ans[id]=res-sum(l-1);}for(int i=0;i<q;i++) cout<<ans[i]<<endl;
}
int main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t=1;cin>>t;while(t--)solve();return 0;
}1006 Perfect square number
法一:
将a[x]修改后区间和为平方数的个数=改之前区间和为平方数的个数-改之前含有x的区间和为平方数的区间个数+改之后含有x的区间和为平方数的区间个数
AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
#include<cstdio>
#define endl '\n'
using namespace std;
typedef long long ll;
const int N=310;
int a[N],s[N];
int n;
//判断x是否是平方数
bool check(int x) {if(pow((int)sqrt(x),2)==x) return true;return false;
}
void solve() {cin>>n;for(int i=1; i<=n; i++) {cin>>a[i];s[i]=s[i-1]+a[i];//前缀和}int res=0;int ans=0;//不重不漏地枚举区间for(int i=1; i<=n; i++) {for(int j=1; j<=i; j++) {if(check(s[i]-s[j-1])) ans++;//ans记录一共有几个区间的区间和为平方数,即记录修改前的个数}}res=ans;for(int x=1; x<=n; x++) {int suml=0;int sum=0;//记录含有x的区间和为平方数的区间个数int cnt[90000]= {0};for(int i=x; i>=1; i--) {suml+=a[i];int sumr=0;for(int j=x; j<=n; j++) {sumr+=a[j];int sumn=suml+sumr-2*a[x];//把x删掉后含有x的区间的区间和为sumnif(check(sumn+a[x])) sum++;//如果含有x的区间和为平方数,那么sum++cnt[sumn]++;//记录去掉x后区间和为sumn的个数}}int f[400]= {0}; //f[i]记录将a[x]修改为i之后含有x的区间和为平方数的区间个数for(int i=1; i<=300; i++) {int m=i*i;//枚举所有的平方数//将a[x]修改为m-jfor(int j=m; j>=0&&m-j<=300; j--) {f[m-j]+=cnt[j];}}for(int i=1; i<=300; i++) {res=max(res,ans-sum+f[i]);}}cout<<res<<endl;
}
int main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t=1;cin>>t;while(t--)solve();return 0;
}法二:
同样是将a[i]修改后区间和为平方数的个数=改之前区间和为平方数的个数-改之前含有i的区间和为平方数的区间个数+改之后含有i的区间和为平方数的区间个数
只不过预处理的方式不一样
算改之前区间和为平方数的个数-改之前含有x的区间和为平方数的区间个数:
通过算区间和为平方数的区间个数前缀和以及区间和为平方数的区间个数后缀和,用数组x记录前缀和,用数组y记录后缀和,比如说我们要修改a[i],那么只要将x[i-1]和y[i+1]加起来即可,这样算出来的就是和i无关的区间和为平方数的区间个数,也就是改之前区间和为平方数的个数-改之前含有i的区间和为平方数的区间个数
接下来就只需要算改之后含有i的区间和为平方数的区间个数
for (int j = i; j <= n; j ++) pre(i, j, 1);
for(int j=1; j<=i-1; j++) pre(j,i-1,-1);着重解释以上两句,我们想的是假设我们要修改第i个数,那么我们枚举与i有关的所有区间,即[i,i],[i,i+1],....[i,n]
以及[1,i],[2,i],...[i-1,i],但是由于我们枚举前面的i时,已经算过了,会导致重复,所以我们只要每次加上以i为左端点的区间就行,例如:
当i为1时,我们枚举以1为左端点的所有区间就已经是与1有关的所有区间了,如图,[1,1],[1,2],[1,3],[1,4],[1,5]
然后我们枚举以2为左端点的所有区间,如图,[2,2],[2,3],[2,4],[2,5],实际上呢,我们仍要枚举以2为右端点的所有区间,我们发现前面已经枚举过了,但是呢,我发现多了[1,1]这个与2无关的区间,所以我们要减去与2无关的区间,即[1,1]

AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
#include<cstdio>
#define endl '\n'
using namespace std;
typedef long long ll;
const int N=610,M=300;
int a[N],s[N];
int x[N],y[N];
int f[N];
int n;
//判断x是否是平方数
bool check(int x) {if(pow((int)sqrt(x),2)==x) return true;return false;
}
void pre(int l, int r, int k) {int sum = s[r] - s[l - 1];//i代表变化值,如果将i修改后,与i有关的区间和为平方数,那么就用数组f记录变化值(加一个M,使得原来从-300到300映射为0到600)的个数for (int i = -M; i <= M; i ++)if (check(sum + i)) f[i + M] += k;
}
void solve() {memset(x,0,sizeof x);memset(y,0,sizeof y);memset(f,0,sizeof f);cin>>n;for(int i=1; i<=n; i++) {cin>>a[i];s[i]=s[i-1]+a[i];//前缀和}//不重不漏地枚举区间for(int i=1; i<=n; i++) {for(int j=1; j<=i; j++) {if(check(s[i]-s[j-1])) x[i]++;//如果区间和为完全平方数,那么以i为右端点的区间和为平方数的区间个数+1}x[i]+=x[i-1];//跑一遍前缀和,数组x记录[1,i]中有多少个区间的区间和为平方数,即区间和为平方数的区间个数前缀和}for(int i=n; i>=1; i--) {for(int j=i; j<=n; j++) {if(check(s[j]-s[i-1])) y[i]++;//如果区间和为平方数,那么以i为左端点的区间和为平方数的区间个数+1}y[i]+=y[i+1];//跑一遍后缀和,数组y记录[i,n]中有多少个区间和为平方数,即区间和为平方数的区间个数后缀和}int res=0;for(int i=1; i<=n; i++) {for (int j = i; j <= n; j ++) pre(i, j, 1);for(int j=1; j<=i-1; j++) pre(j,i-1,-1);//以上两个循环是为了算修改第i个数后的与i有关的区间和为平方数的区间个数(假设f[关键字]=值,那么关键字放的是变化值的映射,值为个数)int now=0;for(int j=1; j<=M; j++) now=max(now,f[j-a[i]+M]);res=max(res,x[i-1]+y[i+1]+now);}cout<<res<<endl;
}
int main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t=1;cin>>t;while(t--)solve();return 0;
}1010 Caclulate
倍增的思想:任何一个十进制数都可以表示为若干个2的次幂的和

手上初始的数字为y,到点i,数字变为ki*y+bi,从点i到点j,数字变为ki*kj*y+kj*bi+bj
所以我们可以先预处理从每一个点走很多很多步的y前面的系数以及b(形式为k*y+b,我们需要预处理k以及b),由于走的步数是十进制数,而且可以达到很大,因为任意一个十进制数都可以由若干个2的次幂的和组成,所以对于每一个点,我们直接预处理从该点每次走2的次幂,那么最多走2的几次幂呢?由于最大到1e9,所以最多走2的30次幂




AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
#include<cstdio>
#define endl '\n'
//#define int long long
using namespace std;
const int mod=1e9+7;
const int N=1e5+10,M=31;
typedef long long ll;
int p[N][M];
ll k[N][M],b[N][M];
int n,q;
int query(){int x,l,y;cin>>x>>l>>y;x=p[x][0];//起点为x,先走一步//枚举2的次幂,比如4的二进制为100,然后和l进行与运算,如果l所对应的二进制的这一位也有1的话,那么该2的次幂就可以是l的一部分for(int i=0;i<M;i++){if((1<<i)&l){y=(y*k[x][i]+b[x][i])%mod;x=p[x][i];} }return y;
}
void solve() {cin>>n>>q;for(int i=1;i<=n;i++) cin>>k[i][0];for(int i=1;i<=n;i++) cin>>b[i][0];for(int i=1;i<=n;i++) cin>>p[i][0];for(int j=1;j<=30;j++){for(int i=1;i<=n;i++){p[i][j]=p[p[i][j-1]][j-1];//p[i][j]表示从位置i走2^j可以由位置i走2^(j-1)到达位置p[i][j-1],再从位置p[i][j-1]走2^(j-1)转移而来k[i][j]=k[i][j-1]*k[p[i][j-1]][j-1]%mod;//k[i][j]表示从点i开始包括i数4个数所对应的y前面的系数b[i][j]=(b[i][j-1]*k[p[i][j-1]][j-1]+b[p[i][j-1]][j-1])%mod;//b[i][j]同理,表示从点i开始包括i数4个数所对应的b}}while(q--) cout<<query()<<endl;
}
int main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t=1;cin>>t;while(t--)solve();return 0;
}相关文章:

(杭电多校)2023“钉耙编程”中国大学生算法设计超级联赛(6)
1001 Count 当k在区间(1n)/2的左边时,如图,[1,k]和[n-k1,n]完全相同,所以就m^(n-k) 当k在区间(1n)/2的右边时,如图,[1,n-k1]和[k,n]完全相同,所以也是m^(n-k) 别忘了特判,当k等于n时,n-k为0,然后a1a1,a2a2,..anan,所以没什么限制,那么就是m^n AC代码: #includ…...

【JavaScript 】浏览器事件处理
1. 什么是浏览器事件? 浏览器事件是指在网页中发生的各种交互和动作,例如用户点击按钮、页面加载完成、输入框文本变化等。通过处理这些事件,可以编写相应的JavaScript代码来实现特定的功能和行为。 2. 常见的浏览器事件 以下是一些常见的浏览器事件及其用途的详细介绍: c…...

(力扣)用两个队列实现栈---C语言
分享一首歌曲吧,希望在枯燥的刷题生活中带给你希望和勇气,加油! 题目: 请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty&#…...

使用 RediSearch 在 Redis 中进行全文检索
原文链接: 使用 RediSearch 在 Redis 中进行全文检索 Redis 大家肯定都不陌生了,作为一种快速、高性能的键值存储数据库,广泛应用于缓存、队列、会话存储等方面。 然而,Redis 在原生状态下并不支持全文检索功能,这使…...
[Microsoft][ODBC 驱动程序管理器] 未发现数据源名称并且未指定默认驱动程序
1.今天开发了一套服务程序,使用的是Odbc连接MySql数据库, 在我本机用VS打开程序时,访问一切正常,当发布出来装在电脑上,连接数据库时提示: [Microsoft][ODBC 驱动程序管理器] 未发现数据源名称并且未指定…...
springboot生成表结构和表数据sql
需求 业务背景是需要某单机程序需要把正在进行的任务导出,然后另一台电脑上单机继续运行,我这里选择的方案是同步SQL形式,并保证ID随机,多个数据库不会重复。 实现 package com.nari.web.controller.demo.controller;import cn…...
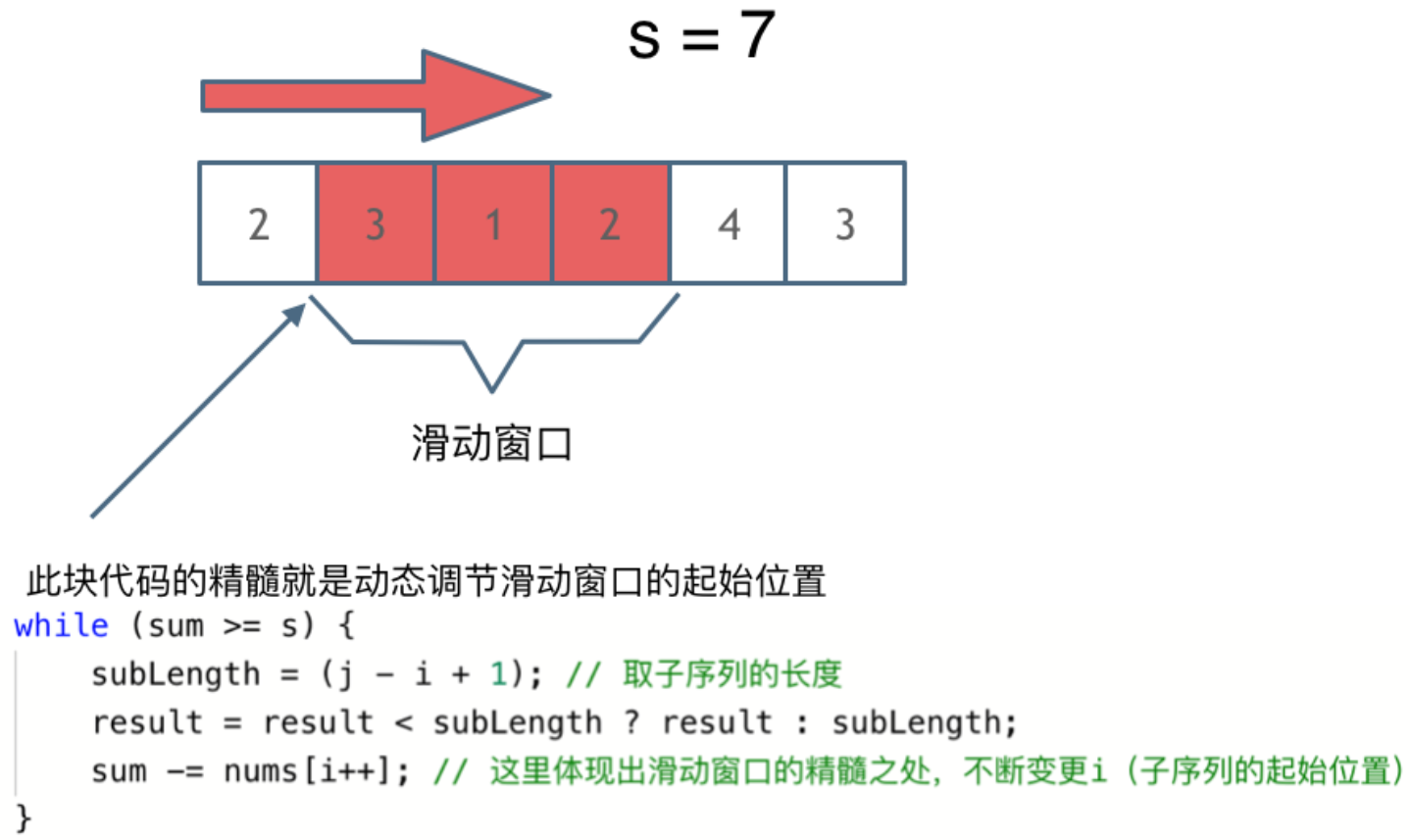
代码随想录—力扣算法题:209长度最小的子数组.Java版(示例代码与导图详解)
版本说明 当前版本号[20230808]。 版本修改说明20230808初版 目录 文章目录 版本说明目录209.长度最小的子数组思路暴力解法滑动窗口 两种方法的区别总结 209.长度最小的子数组 力扣题目链接 更多内容可点击此处跳转到代码随想录,看原版文件 给定一个含有 n 个…...

81 | Python可视化篇 —— Seaborn数据可视化
Seaborn是Python中一个基于Matplotlib的高级数据可视化库,它提供了更简单的API和更美观的图形样式,适用于数据探索和展示。在本教程中,我们将介绍Seaborn的基本概念和用法,并通过一些示例演示如何使用Seaborn来创建各种图表和图形。 文章目录 1. 导入Seaborn库和数据2. 数据…...
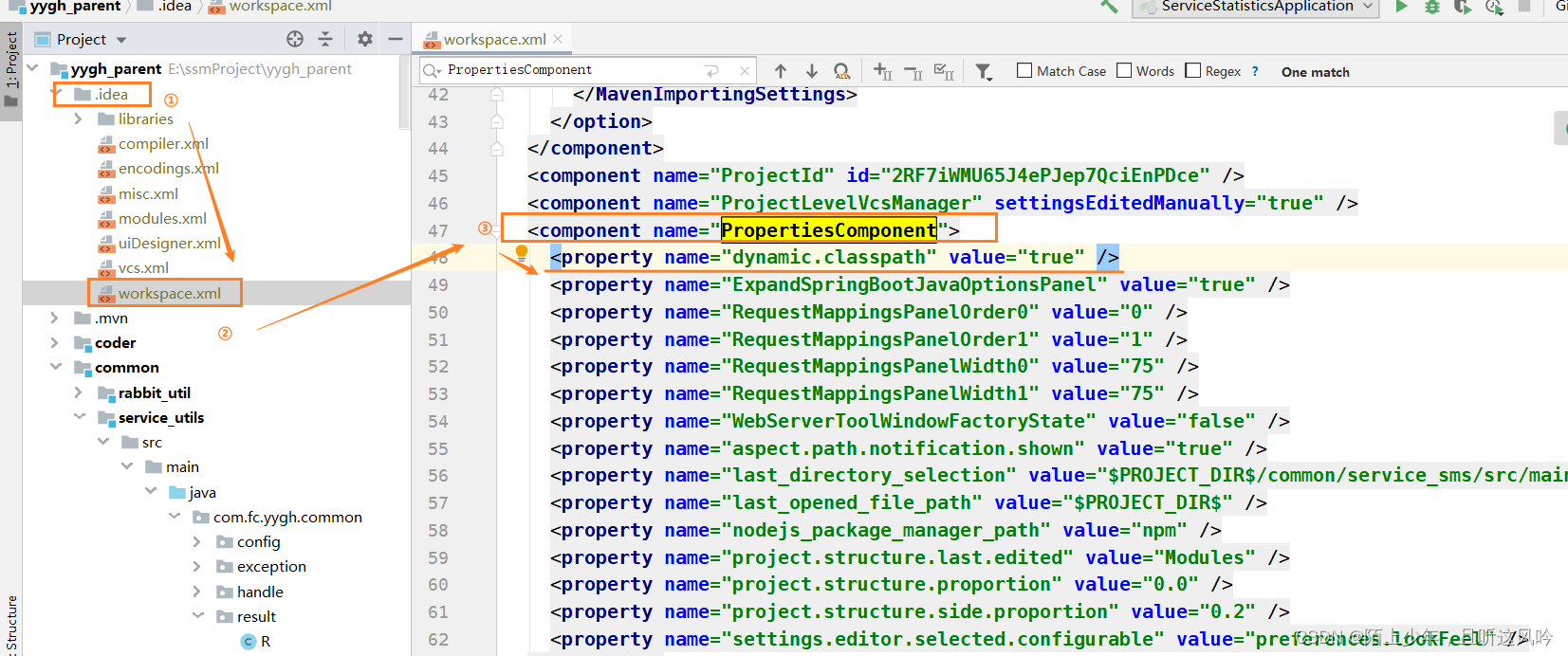
解决Error running XXXApplicationCommand line is too long.报错
测试IDEA版本:2019.2.4 ,2020.1.3 文章目录 一. 问题场景二. 报错原因2.1 为什么命令行过长会导致这种问题? 三. 解决方案3.1 方案一3.2 方案二 一. 问题场景 当我们从GitHub或公司自己搭建的git仓库上拉取项目代码时,会出现以下错误 报错代…...

【Linux】—— 进程等待 waitwaitpid
序言: 之前讲过,子进程退出,父进程如果不管不顾,就可能造成‘僵尸进程’的问题,进而造成内存泄漏。因此,为了解决这个问题,就需要用到有关 “进程等待” 的基本知识!!&am…...

el-tree 懒加载数据,增删改时局部刷新实现
1.数据过多时进行懒加载孩子节点,根据层级传参获取后端孩子数据 懒加载主要部分: 1参数: :load"loadNode" lazy :props"defaultProps" 2.defaultProps 需要设置isLeaf: isLeaf,去除最后一层孩子节点的展开图表 defaultProps: { ch…...
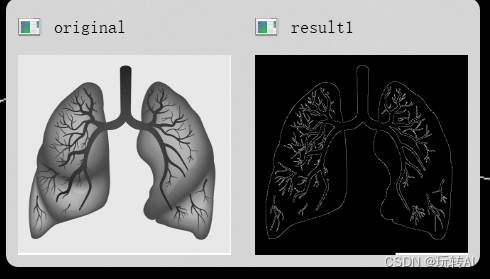
opencv基础44- Canny边缘检测详解-cv.Canny()
什么是Canny边缘检测? Canny边缘检测是一种经典的边缘检测算法,由John F. Canny在1986年提出。它被广泛应用于计算机视觉和图像处理领域,是一种多阶段的边缘检测算法,能够有效地检测图像中的边缘并抑制噪声。 Canny边缘检测的主要…...
--函数)
neo4j查询语言Cypher详解(三)--函数
函数 Cypher中的函数如果输入参数为null,则返回null。 以字符串作为输入的函数都对Unicode字符进行操作,而不是对标准字符进行操作。例如,size()函数应用于任何Unicode字符将返回1,即使该字符不适合一个字符的16位。 可以通过 …...

kafka权威指南(阅读摘录)
零复制 Kafka 使用零复制技术向客户端发送消息——也就是说,Kafka 直接把消息从文件(或者更确切地说是 Linux 文件系统缓存)里发送到网络通道,而不需要经过任何中间缓冲区。这是 Kafka 与其他大部分数据库系统不一样的地方&#…...
【爬虫实践】使用Python从网站抓取数据
一、说明 本周我不得不为客户抓取一个网站。我意识到我做得如此自然和迅速,分享它会很有用,这样你也可以掌握这门艺术。【免责声明:本文展示了我的抓取做法,如果您有更多相关做法请在评论中分享】 二、计划策略 2.1 策划 确定您…...
win10 2022unity设置中文
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言解决方法 前言 在Edit->preferences里找不到language选项。 解决方法 【1】打开下面地址 注意 :把{version}换成你当前安装的版本,比如说如果…...

python表白代码大全可复制,python表白代码大全简单
大家好,小编来为大家解答以下问题,python表白代码大全可复制,python表白程序代码完整版,现在让我们一起来看看吧! 今天是20230520,有人说:5代表的是人生五味,酸甜苦辣咸;…...

wordpress 打开缓慢处理
gravatar.com 头像网站被墙 追踪发现请求头像时长为21秒 解决方案一 不推荐,容易失效,网址要是要稳定为主,宁愿头像显示异常,也不能网址打不开 网上大部分搜索到的替换的CDN网址都过期了,例如:gravatar.du…...
Adobe ColdFusion 反序列化漏洞复现(CVE-2023-29300)
0x01 产品简介 Adobe ColdFusion是美国奥多比(Adobe)公司的一套快速应用程序开发平台。该平台包括集成开发环境和脚本语言。 0x02 漏洞概述 Adobe ColdFusion存在代码问题漏洞,该漏洞源于受到不受信任数据反序列化漏洞的影响,攻击…...

林【2018】
关键字: BST插入叶子结点、ADT结伴操作、队列插入前r-1、哈希函数二次探测法(1,-1,4,-4)、队列元素个数、折半查找失败次数、广义表链表结构、B-树构建、单链表指定位置插入数组元素 一、判断 二、单选 h(49)+1,-1,+4,-4...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...
