代码随想录—力扣算法题:209长度最小的子数组.Java版(示例代码与导图详解)
版本说明
当前版本号[20230808]。
| 版本 | 修改说明 |
|---|---|
| 20230808 | 初版 |
目录
文章目录
- 版本说明
- 目录
- 209.长度最小的子数组
- 思路
- 暴力解法
- 滑动窗口
- 两种方法的区别
- 总结
209.长度最小的子数组
力扣题目链接
更多内容可点击此处跳转到代码随想录,看原版文件
给定一个含有 n 个正整数的数组和一个正整数 s ,找出该数组中满足其和 ≥ s 的长度最小的 连续 子数组,并返回其长度。如果不存在符合条件的子数组,返回 0。
示例:
- 输入:s = 7, nums = [2,3,1,2,4,3]
- 输出:2
- 解释:子数组 [4,3] 是该条件下的长度最小的子数组。
提示:
- 1 <= target <= 10^9
- 1 <= nums.length <= 10^5
- 1 <= nums[i] <= 10^5
思路
暴力解法
这道题目暴力解法当然是 两个for循环,然后不断的寻找符合条件的子序列,时间复杂度很明显是O(n^2)。
代码如下:
class Solution {/*** 使用滑动窗口方法来找到最小长度的子数组*s 目标值* nums正整数数组* 最小长度的子数组的长度*/public int minSubArrayLen(int s, int[] nums) {int result = Integer.MAX_VALUE; // 最终的结果,默认为最大值int sum = 0; // 子序列的数值之和int subLength = 0; // 子序列的长度for (int i = 0; i < nums.length; i++) { // 设置子序列起点为isum = 0;for (int j = i; j < nums.length; j++) { // 设置子序列终止位置为jsum += nums[j];if (sum >= s) { // 一旦发现子序列和超过了s,更新resultsubLength = j - i + 1; // 取子序列的长度result = Math.min(result, subLength); // 更新result为较小值break; // 因为我们是找符合条件最短的子序列,所以一旦符合条件就break}}}// 如果result没有被赋值的话,就返回0,说明没有符合条件的子序列return result == Integer.MAX_VALUE ? 0 : result;}
}
- 时间复杂度:O(n^2)
- 空间复杂度:O(1)
后面力扣更新了数据,暴力解法已经超时了。
滑动窗口
接下来就开始介绍数组操作中另一个重要的方法:滑动窗口。
所谓滑动窗口,就是不断的调节子序列的起始位置和终止位置,从而得出我们要想的结果。
在暴力解法中,是一个for循环滑动窗口的起始位置,一个for循环为滑动窗口的终止位置,用两个for循环 完成了一个不断搜索区间的过程。
那么滑动窗口如何用一个for循环来完成这个操作呢?
首先要思考 如果用一个for循环,那么应该表示 滑动窗口的起始位置,还是终止位置。
如果只用一个for循环来表示 滑动窗口的起始位置,那么如何遍历剩下的终止位置?
此时难免再次陷入 暴力解法的怪圈。
所以 只用一个for循环,那么这个循环的索引,一定是表示 滑动窗口的终止位置。
那么问题来了, 滑动窗口的起始位置如何移动呢?
这里还是以题目中的示例来举例,s=7, 数组是 2,3,1,2,4,3,来看一下查找的过程:
第一步:设i,j为滑动窗口开始、终止位置

第二步:i开始向右走,直到走到累加的和大于等于7停下来
2 + 3 = 5 < 7
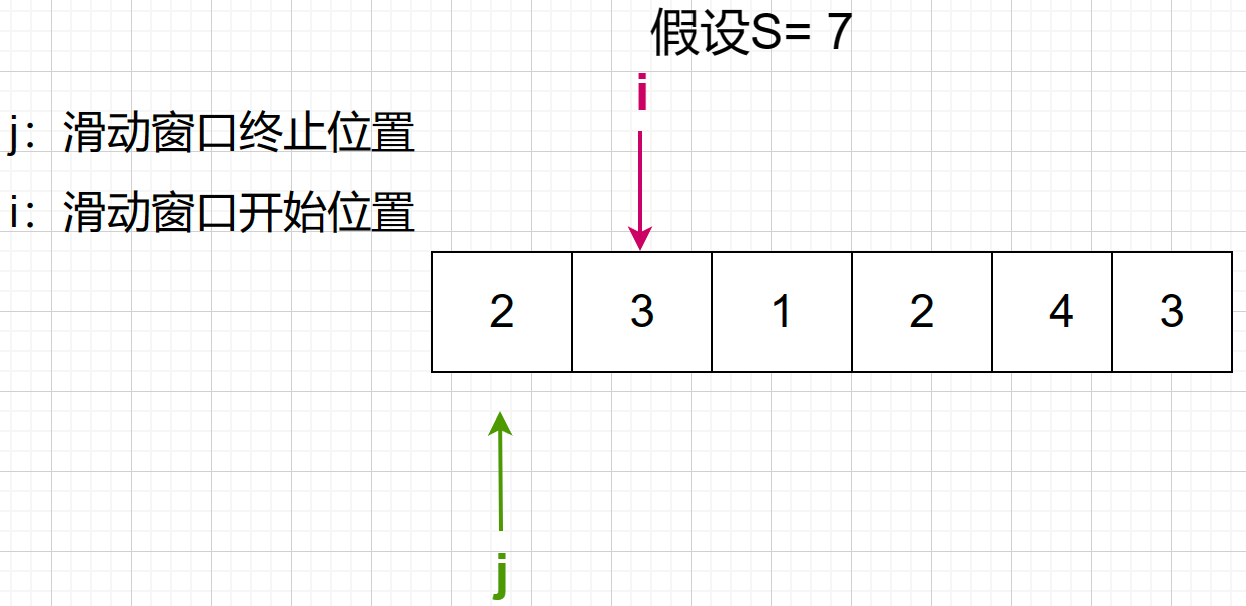
2 + 3 + 1 = 6 < 7
2 + 3 + 1 + 2 = 8 > 7 ,长度为4
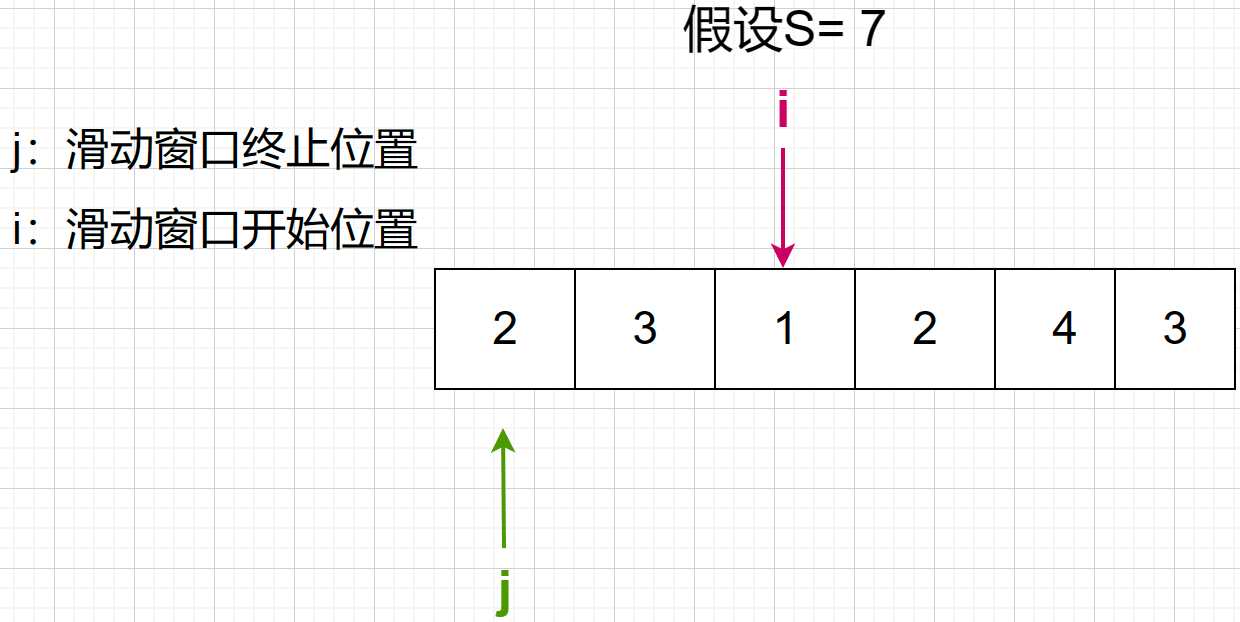
第三步,当出现i累加的和大于等于7并且已经停下来后,终止位置j开始向右移动,当走到滑动窗口不再大于等于7就停下来
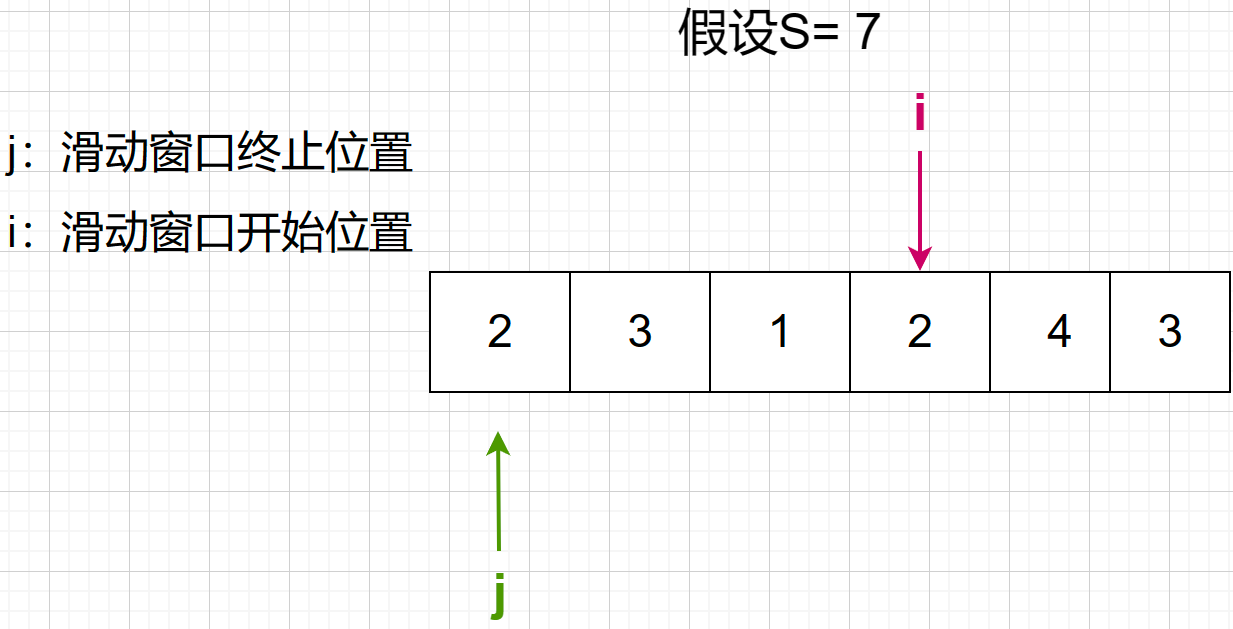
第四步,此时滑动窗口已不再大于等于7了,i就可以继续向右走了
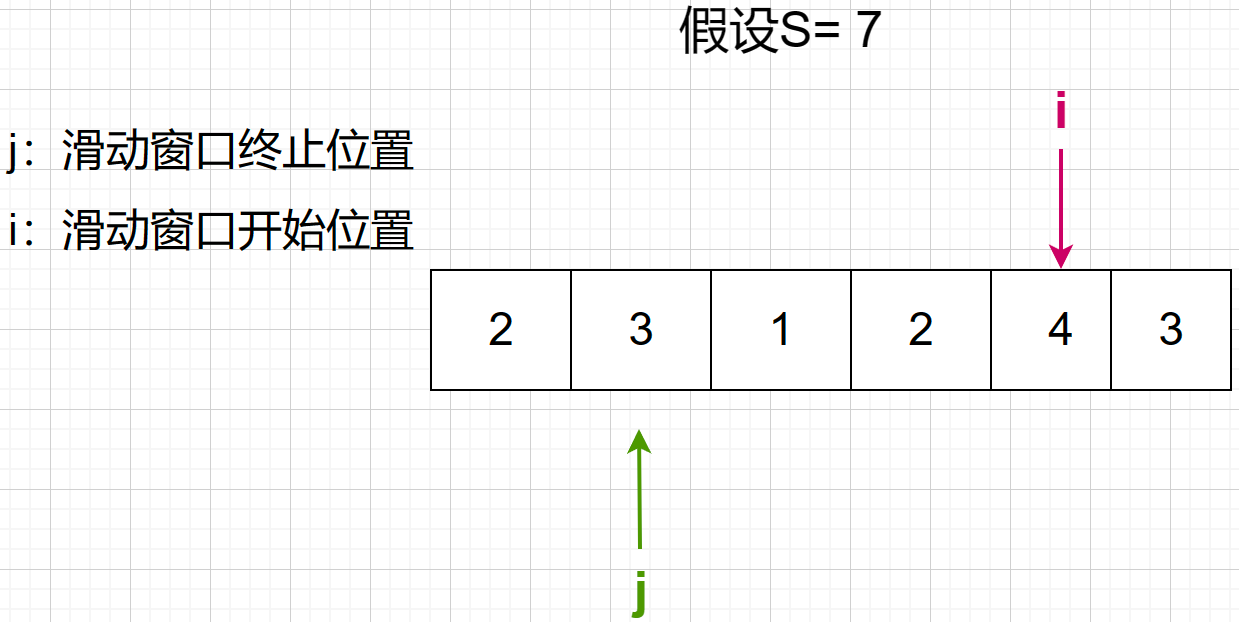
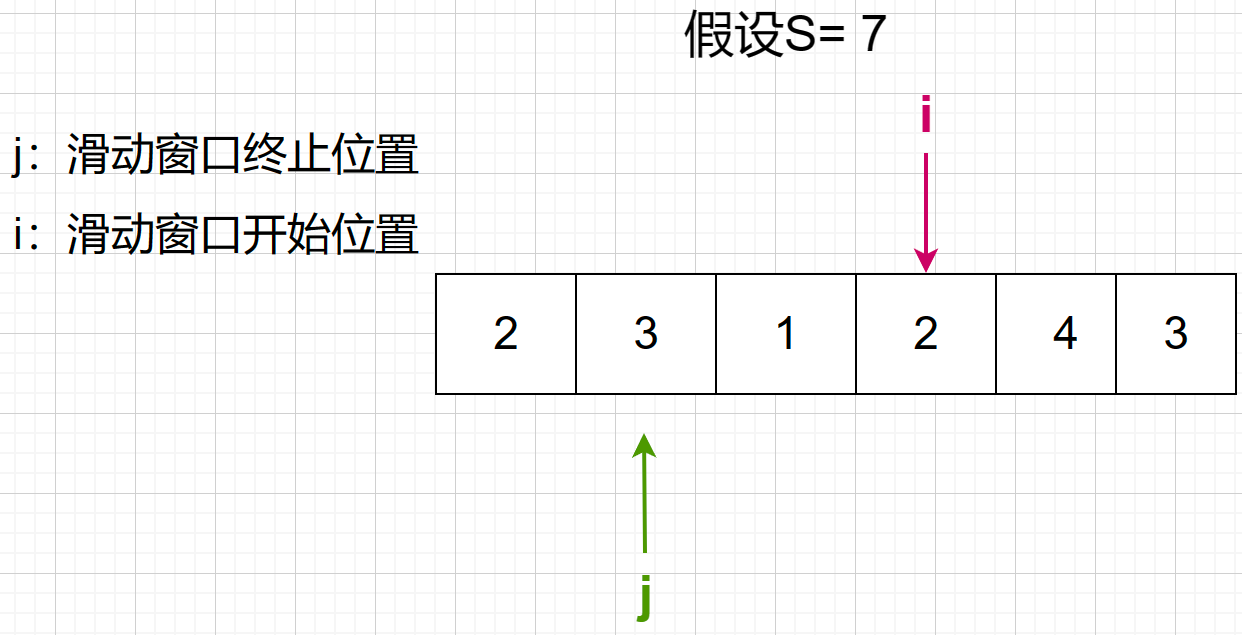
第五步,此时,滑动窗口已经大于等于7了,j就向右移到滑动窗口不大于等于7的位置就可以了,会发现1 + 2 + 4 = 7,需要继续向右走 ,长度为3
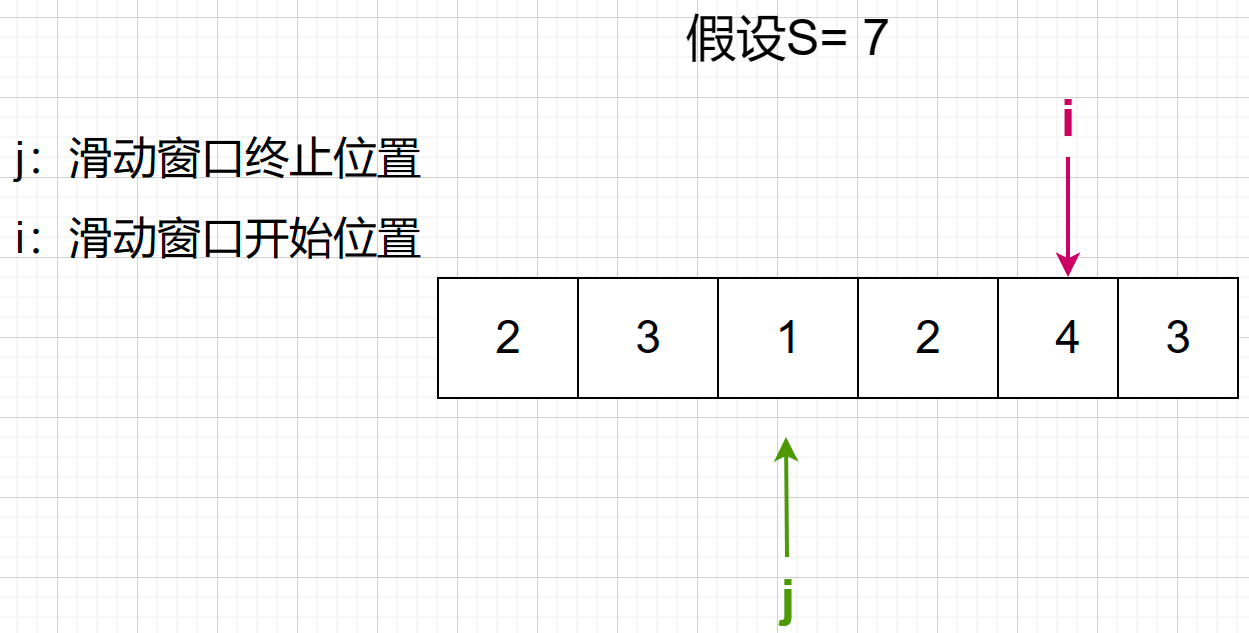
2 + 4 < 7,j停止走动

第六步,滑动窗口不再大于等于7了,i继续向右走

第七步,滑动窗口已大于等于7了,2 + 4 + 3 = 9 < 7 ,长度为3 , j继续向下移动
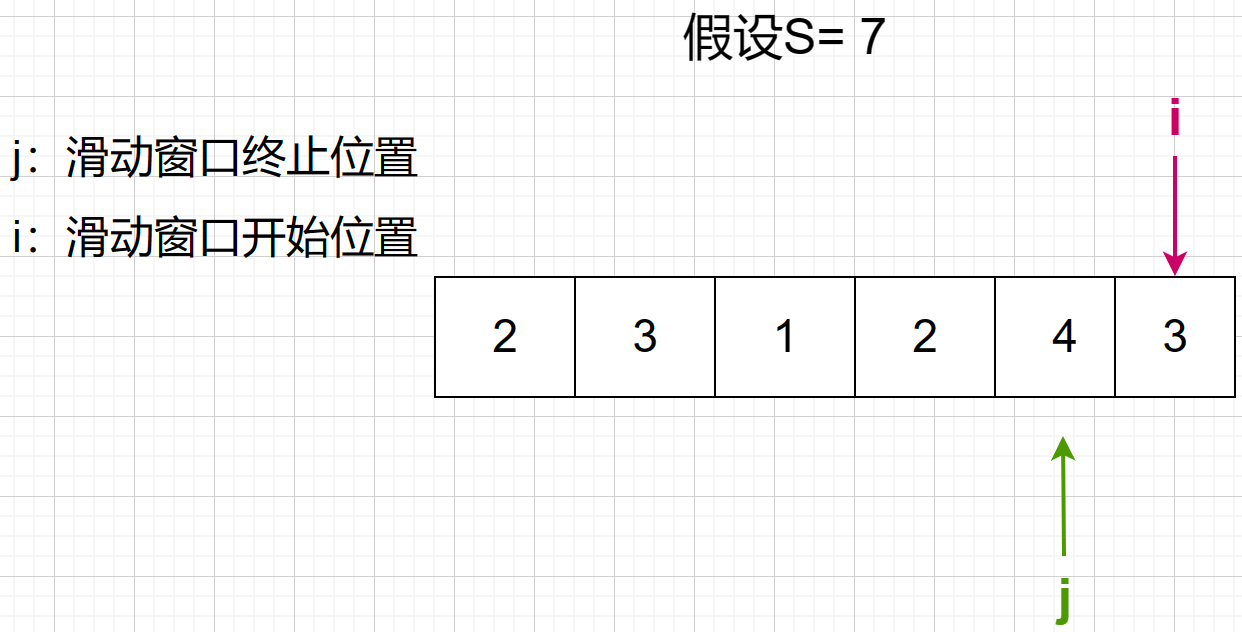
最后找到 4,3 ,长度为2, 是最短距离。
其实从动画中可以发现**滑动窗口也可以理解为双指针法的一种!**只不过这种解法更像是一个窗口的移动,所以叫做滑动窗口更适合一些。
在本题中实现滑动窗口,主要确定如下三点:
- 窗口内是什么?
- 如何移动窗口的起始位置?
- 如何移动窗口的结束位置?
窗口就是 满足其和 ≥ s 的长度最小的 连续 子数组。
窗口的起始位置如何移动:如果当前窗口的值大于s了,窗口就要向前移动了(也就是该缩小了)。
窗口的结束位置如何移动:窗口的结束位置就是遍历数组的指针,也就是for循环里的索引。
解题的关键在于 窗口的起始位置如何移动,如图所示:
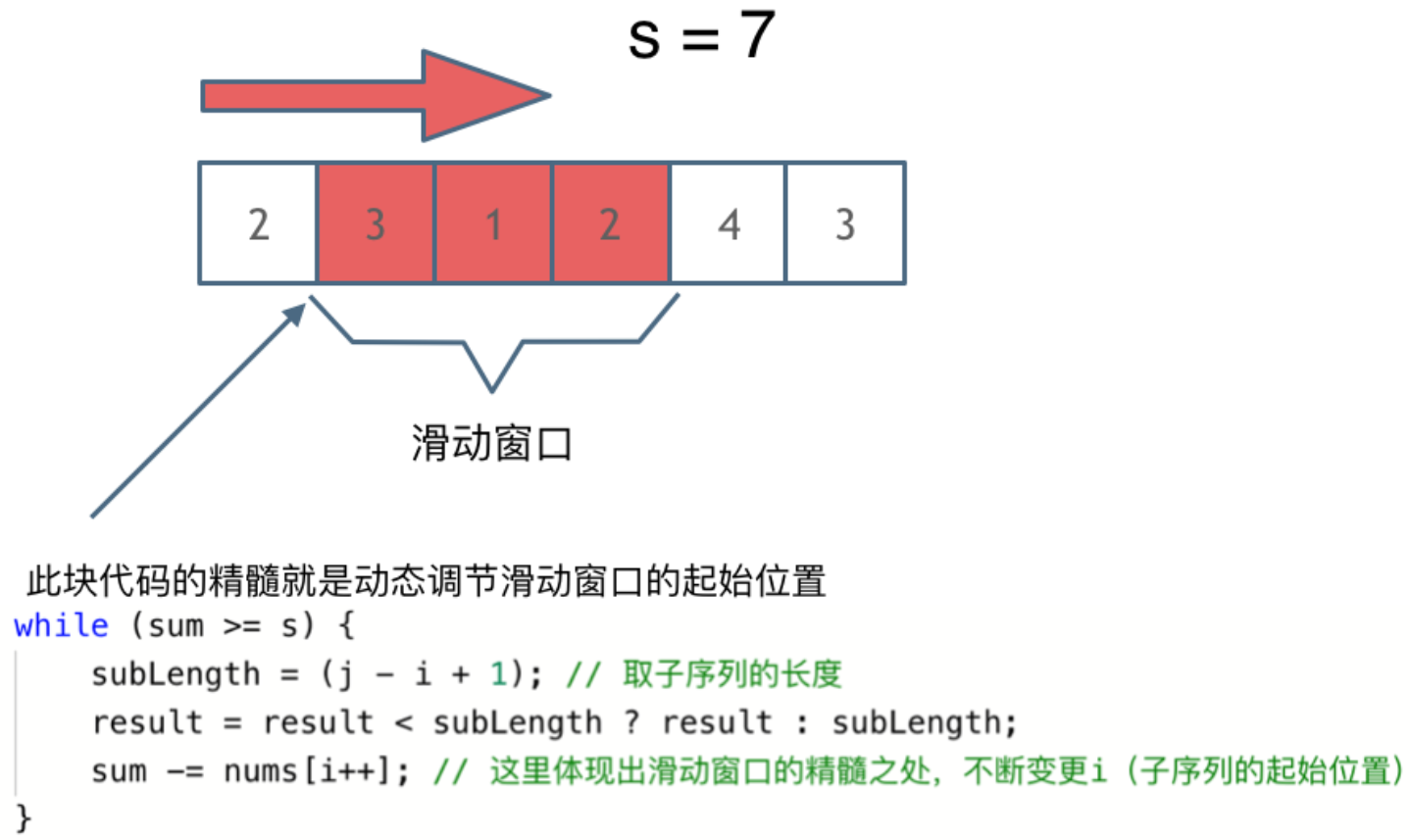
可以发现滑动窗口的精妙之处在于根据当前子序列和大小的情况,不断调节子序列的起始位置。从而将O(n^2)暴力解法降为O(n)。
代码如下:
class Solution {/*** 使用滑动窗口方法来找到最小长度的子数组* s 目标值*nums 正整数数组*return 最小长度的子数组的长度*/public int minSubArrayLen(int s, int[] nums) {int left = 0; // 左指针int sum = 0; // 当前滑动窗口的和int result = Integer.MAX_VALUE; // 最小长度,默认为最大值for (int right = 0; right < nums.length; right++) { // 右指针遍历数组sum += nums[right]; // 将当前元素加入滑动窗口的和while (sum >= s) { // 当滑动窗口的和大于等于目标值result = Math.min(result, right - left + 1); // 更新最小长度sum -= nums[left++]; // 左指针右移,从滑动窗口的和中减去左边界的元素}}return result == Integer.MAX_VALUE ? 0 : result; // 返回最小长度,如果不存在满足条件的子数组,则返回0}
}
- 时间复杂度:O(n)
- 空间复杂度:O(1)
一些录友会疑惑为什么时间复杂度是O(n)。
不要以为for里放一个while就以为是O(n^2)啊, 主要是看每一个元素被操作的次数,每个元素在滑动窗后进来操作一次,出去操作一次,每个元素都是被操作两次,所以时间复杂度是 2 × n 也就是O(n)。
两种方法的区别
暴力解法和滑动窗口方法之间的区别如下:
- 暴力解法:
- 暴力解法是一种简单直接的方法,在给定数组中遍历所有可能的连续子数组,计算它们的和,然后找到满足和大于等于目标值s的最小长度。
- 具体操作是使用两个嵌套的for循环,外层循环遍历所有可能的起始位置,内层循环遍历以当前起始位置为起点的所有连续子数组。
- 对于每个子数组,计算它们的和并与目标值s进行比较。如果和大于等于目标值s,则更新最小长度。
- 这种方法的时间复杂度为O(n^2),因为需要遍历所有可能的子数组。在最坏的情况下,数组中可能会有n个连续子数组。
- 空间复杂度为O(1),因为只使用了常数级别的额外空间。
- 滑动窗口方法:
- 滑动窗口方法使用两个指针来构建滑动窗口,左指针和右指针分别表示滑动窗口的左边界和右边界。
- 首先,将左指针和右指针都指向数组的第一个元素。
- 然后,移动右指针,将元素逐个加到滑动窗口的和中,直到滑动窗口的和大于等于目标值s为止。
- 当滑动窗口的和大于等于目标值s时,记录当前滑动窗口的长度,并更新最小长度。
- 然后,移动左指针,将滑动窗口的左边界向右移动一位,并从滑动窗口的和中减去左边界的元素。
- 重复上述步骤,直到右指针达到数组的末尾。
- 这种方法的时间复杂度为O(n),因为每个元素最多被访问两次(左指针和右指针),没有遍历所有可能的子数组。
- 空间复杂度为O(1),除了常数级别的几个变量外,没有使用额外的空间。
对于给定的示例输入s = 7, nums = [2,3,1,2,4,3],滑动窗口方法可以在O(n)的时间复杂度内找到满足条件的最小长度子数组,而暴力解法则需要O(n^2)的时间复杂度。因此,滑动窗口方法更高效。
总结
- 使用滑动窗口方法可以解决这个问题。定义两个指针,分别表示滑动窗口的左右边界。
- 初始化左指针和右指针都指向数组的第一个元素。
- 然后,移动右指针,将元素逐个加到滑动窗口的和中,直到滑动窗口的和大于等于目标值s为止。
- 当滑动窗口的和大于等于目标值s时,记录当前滑动窗口的长度,并更新最小长度。
- 然后,移动左指针,将滑动窗口的左边界向右移动一位,并从滑动窗口的和中减去左边界的元素。
- 重复步骤3到步骤5,直到右指针达到数组的末尾。
- 返回最小长度,如果不存在满足条件的子数组,则返回0。
- 时间复杂度分析:使用滑动窗口,每个元素最多会被访问两次(左指针和右指针),所以时间复杂度为O(n)。
- 空间复杂度分析:空间复杂度为O(1)。除了常数级别的几个变量外,没有使用额外的空间。
调用minSubArrayLen方法进行测试。将给定的数组nums和目标值s传递给方法,并将返回结果打印出来。预期输出为2,这是因为数组中的子数组[4, 3]的元素之和为7,且为满足条件的最小长度子数组。
测试代码:
package shuzhu;public class Day04 {public static int minSubArrayLen(int[] nums, int s) {int left = 0;int sum = 0;int result = Integer.MAX_VALUE;for(int right = 0;right < nums.length;right++){sum += nums[right];while(sum >= s){result = Math.min(result, right-left+1);sum -= nums[left++];}}return result == Integer.MAX_VALUE ? 0 : result;}public static void main(String[] args) {int[] nums = {2, 3, 1, 2, 4, 3};int s = 7;int result =minSubArrayLen(nums, s);System.out.println("长度最小的连续数组其长度为:"+result);}
}return result == Integer.MAX_VALUE ? 0 : result;}public static void main(String[] args) {int[] nums = {2, 3, 1, 2, 4, 3};int s = 7;int result =minSubArrayLen(nums, s);System.out.println("长度最小的连续数组其长度为:"+result);}
}
相关文章:

代码随想录—力扣算法题:209长度最小的子数组.Java版(示例代码与导图详解)
版本说明 当前版本号[20230808]。 版本修改说明20230808初版 目录 文章目录 版本说明目录209.长度最小的子数组思路暴力解法滑动窗口 两种方法的区别总结 209.长度最小的子数组 力扣题目链接 更多内容可点击此处跳转到代码随想录,看原版文件 给定一个含有 n 个…...

81 | Python可视化篇 —— Seaborn数据可视化
Seaborn是Python中一个基于Matplotlib的高级数据可视化库,它提供了更简单的API和更美观的图形样式,适用于数据探索和展示。在本教程中,我们将介绍Seaborn的基本概念和用法,并通过一些示例演示如何使用Seaborn来创建各种图表和图形。 文章目录 1. 导入Seaborn库和数据2. 数据…...
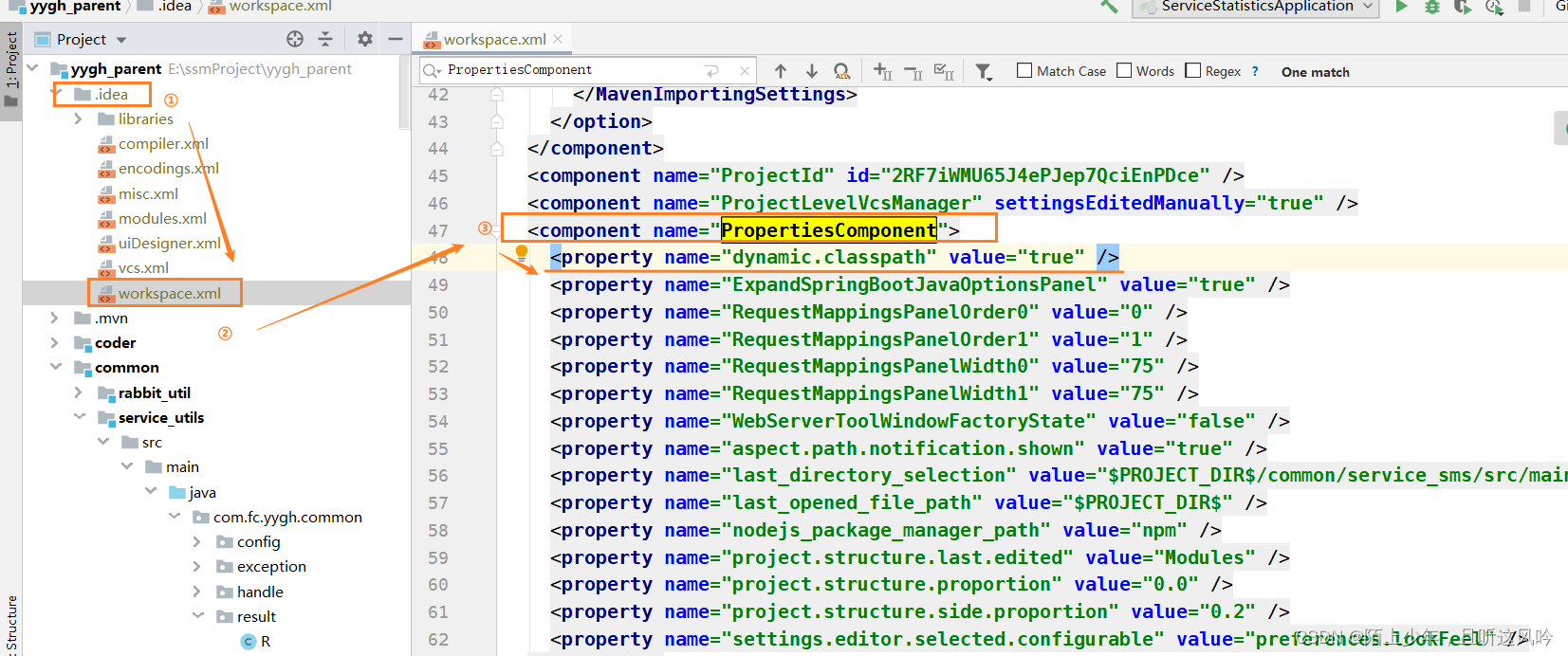
解决Error running XXXApplicationCommand line is too long.报错
测试IDEA版本:2019.2.4 ,2020.1.3 文章目录 一. 问题场景二. 报错原因2.1 为什么命令行过长会导致这种问题? 三. 解决方案3.1 方案一3.2 方案二 一. 问题场景 当我们从GitHub或公司自己搭建的git仓库上拉取项目代码时,会出现以下错误 报错代…...

【Linux】—— 进程等待 waitwaitpid
序言: 之前讲过,子进程退出,父进程如果不管不顾,就可能造成‘僵尸进程’的问题,进而造成内存泄漏。因此,为了解决这个问题,就需要用到有关 “进程等待” 的基本知识!!&am…...

el-tree 懒加载数据,增删改时局部刷新实现
1.数据过多时进行懒加载孩子节点,根据层级传参获取后端孩子数据 懒加载主要部分: 1参数: :load"loadNode" lazy :props"defaultProps" 2.defaultProps 需要设置isLeaf: isLeaf,去除最后一层孩子节点的展开图表 defaultProps: { ch…...
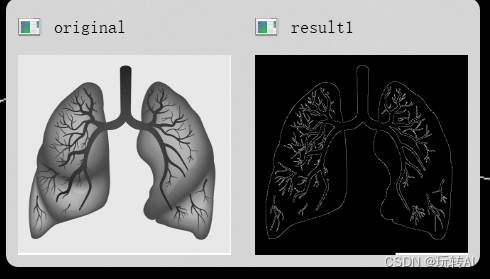
opencv基础44- Canny边缘检测详解-cv.Canny()
什么是Canny边缘检测? Canny边缘检测是一种经典的边缘检测算法,由John F. Canny在1986年提出。它被广泛应用于计算机视觉和图像处理领域,是一种多阶段的边缘检测算法,能够有效地检测图像中的边缘并抑制噪声。 Canny边缘检测的主要…...
--函数)
neo4j查询语言Cypher详解(三)--函数
函数 Cypher中的函数如果输入参数为null,则返回null。 以字符串作为输入的函数都对Unicode字符进行操作,而不是对标准字符进行操作。例如,size()函数应用于任何Unicode字符将返回1,即使该字符不适合一个字符的16位。 可以通过 …...

kafka权威指南(阅读摘录)
零复制 Kafka 使用零复制技术向客户端发送消息——也就是说,Kafka 直接把消息从文件(或者更确切地说是 Linux 文件系统缓存)里发送到网络通道,而不需要经过任何中间缓冲区。这是 Kafka 与其他大部分数据库系统不一样的地方&#…...
【爬虫实践】使用Python从网站抓取数据
一、说明 本周我不得不为客户抓取一个网站。我意识到我做得如此自然和迅速,分享它会很有用,这样你也可以掌握这门艺术。【免责声明:本文展示了我的抓取做法,如果您有更多相关做法请在评论中分享】 二、计划策略 2.1 策划 确定您…...
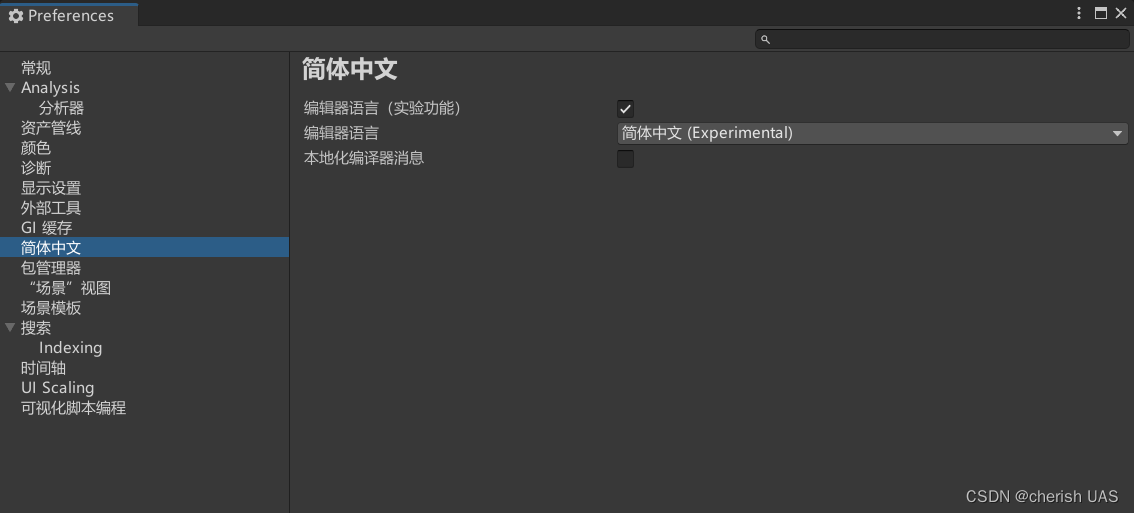
win10 2022unity设置中文
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言解决方法 前言 在Edit->preferences里找不到language选项。 解决方法 【1】打开下面地址 注意 :把{version}换成你当前安装的版本,比如说如果…...

python表白代码大全可复制,python表白代码大全简单
大家好,小编来为大家解答以下问题,python表白代码大全可复制,python表白程序代码完整版,现在让我们一起来看看吧! 今天是20230520,有人说:5代表的是人生五味,酸甜苦辣咸;…...

wordpress 打开缓慢处理
gravatar.com 头像网站被墙 追踪发现请求头像时长为21秒 解决方案一 不推荐,容易失效,网址要是要稳定为主,宁愿头像显示异常,也不能网址打不开 网上大部分搜索到的替换的CDN网址都过期了,例如:gravatar.du…...
Adobe ColdFusion 反序列化漏洞复现(CVE-2023-29300)
0x01 产品简介 Adobe ColdFusion是美国奥多比(Adobe)公司的一套快速应用程序开发平台。该平台包括集成开发环境和脚本语言。 0x02 漏洞概述 Adobe ColdFusion存在代码问题漏洞,该漏洞源于受到不受信任数据反序列化漏洞的影响,攻击…...

林【2018】
关键字: BST插入叶子结点、ADT结伴操作、队列插入前r-1、哈希函数二次探测法(1,-1,4,-4)、队列元素个数、折半查找失败次数、广义表链表结构、B-树构建、单链表指定位置插入数组元素 一、判断 二、单选 h(49)+1,-1,+4,-4...
ffmpeg+nginx实现rtsp协议摄像头web端播放
ffmpegnginx实现rtsp协议摄像头web端播放 环境准备准备nginx环境添加rtmp模块添加hls转发 使用ffmpeg,将摄像头rtsp转为rtmp并推送到nginxVLC播放验证 环境准备 nginx(需要安装rtmp模块)ffmpeg 6.0vlc播放器(本地播放验证&#x…...

【周赛第69期】满分题解 软件工程选择题 枚举 dfs
目录 选择题1.2.3.4.面向对象设计七大原则 编程题S数最小H值 昨晚没睡好,脑子不清醒,痛失第1名 选择题 1. 关于工程效能,以下哪个选项可以帮助提高团队的开发效率? A、频繁地进行代码审查 B、使用自动化测试工具 C、使用版本控…...

P2015 二叉苹果树
P2015 二叉苹果树 类似于带限制背包问题,但不知道也能做。 n , q n,q n,q 范围小,大胆设 dp 状态。设 f u , i \large f_{u,i} fu,i 表示 u u u 子树内保留 i i i 根树枝的最大苹果数,可得状态转移方程 f u , i f u , j f v , i − …...

Linux 内核音频数据传递主要流程
Linux 用户空间应用程序通过声卡驱动程序(一般牵涉到多个设备驱动程序)和 Linux 内核 ALSA 框架导出的 PCM 设备文件,如 /dev/snd/pcmC0D0c 和 /dev/snd/pcmC0D0p 等,与 Linux 内核音频设备驱动程序和音频硬件进行数据传递。PCM 设…...

torch.device函数
torch.device 是 PyTorch 中用于表示计算设备(如CPU或GPU)的类。它允许你在代码中指定你希望在哪个设备上执行张量和模型操作,本文主要介绍了 torch.device 函数的用法和功能。 本文主要包含以下内容: 1.创建设备对象2.将张量和模…...
火车头采集器AI伪原创【php源码】
大家好,本文将围绕python作业提交什么文件展开说明,python123怎么提交作业是一个很多人都想弄明白的事情,想搞清楚python期末作业程序需要先了解以下几个事情。 火车头采集ai伪原创插件截图: I have a python project, whose fold…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...
