当前位置： 首页 > news >正文

[HDLBits] Mt2015 q4a

news 2026/2/10 22:37:07

Module A is supposed to implement the function z = (x^y) & x. Implement this module.

module top_module (input x, input y, output z);assign z=(x^y)&x;
endmodule

 

相关文章：

[HDLBits] Mt2015 q4a

Module A is supposed to implement the function z (x^y) & x. Implement this module. module top_module (input x, input y, output z);assign z(x^y)&x; endmodule...

编程日记 2023/8/9 3:17:03

HarmonyOS NEXT，生命之树初长成

在不同的神话体系中，都有着关于生命之树的记载。 比如在北欧神话中，一株巨大的树木联结着九大世界，其被称为“尤克特拉希尔”Yggdrasill。在中国的《山海经》中，也有着“建木”的传说，它“有九欘，下有九枸&…...

编程日记 2023/8/9 3:16:02

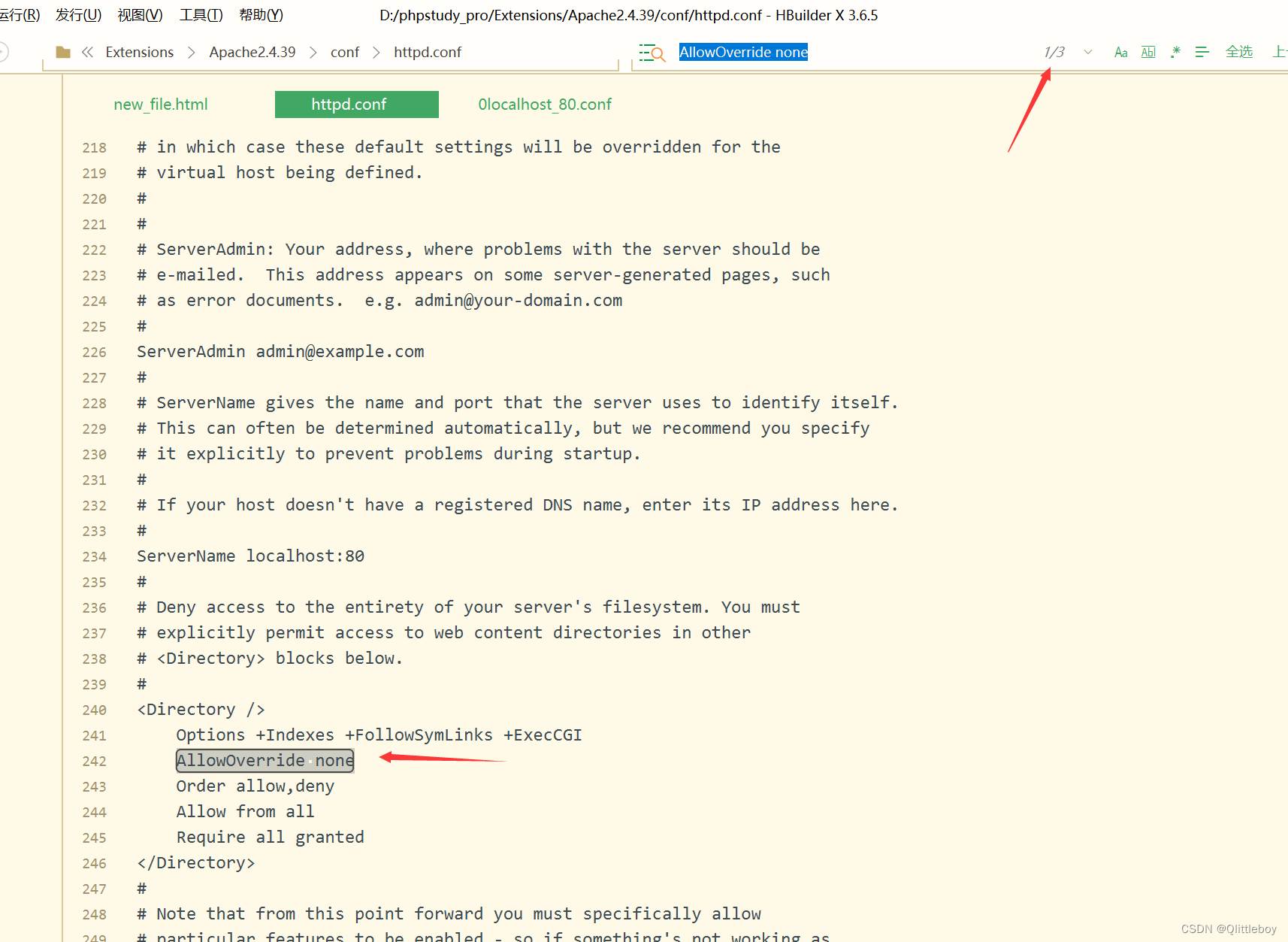
PHPstudy配置伪静态步骤，tp5.1的框架

搜索mod_rewrite.so&#xff0c;然后去掉前面的#&#xff08;即放开注释&#xff09; 2.找到index.php 同级文件.htaccess&#xff08;没有就新建&#xff09; 这些是tp5.1自带的内容&#xff0c;把它注释掉&#xff0c;是错误的内容&#xff0c;添加下面的这段配置 #<If…...

编程日记 2023/8/9 3:14:59

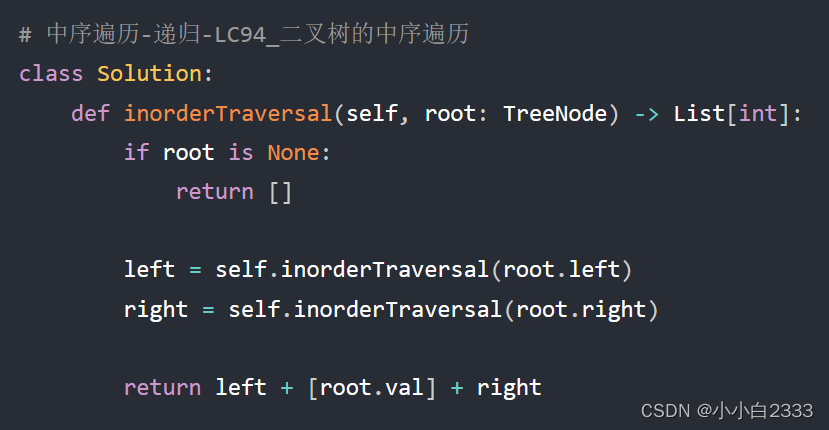
LeetCode:Hot100的python版本

94. 二叉树的中序遍历...

编程日记 2023/8/9 3:13:58

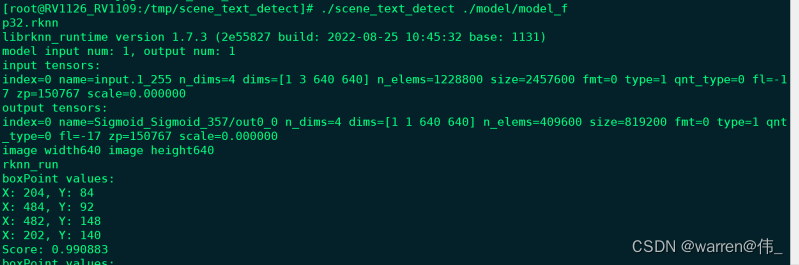
rv1126更新rknpu驱动教学

测试平台&#xff1a;易佰纳rv1126 38板 查看板端版本-------------------------------------------------- 1&#xff1a;查看npu驱动版本 dmesg | grep -i galcore&#xff0c;可以看到版本为6.4.3.5 2&#xff1a;查看rknn-server版本 strings /usr/bin/rknn_server | g…...

编程日记 2023/8/9 3:12:56

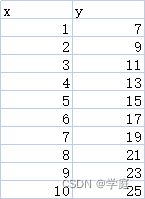
[机器学习]线性回归模型

线性回归 线性回归&#xff1a;根据数据&#xff0c;确定两种或两种以上变量间相互依赖的定量关系 函数表达式&#xff1a; y f ( x 1 , x 2 . . . x n ) y f(x_1,x_2...x_n) yf(x1​,x2​...xn​) ​ 回归根据变量数分为一元回归[ y f ( x ) yf(x) yf(x)]和多元回归[ y …...

编程日记 2023/8/9 3:11:55

Vue基于php医院预约挂号系统_6nrhh

随着信息时代的来临&#xff0c;过去的管理方式缺点逐渐暴露&#xff0c;对过去的医院预约挂号管理方式的缺点进行分析&#xff0c;采取计算机方式构建医院预约挂号系统。本文通过阅读相关文献&#xff0c;研究国内外相关技术&#xff0c;开发并设计一款医院预约挂号系统的构建…...

编程日记 2023/8/9 3:10:54

2023-08-07力扣今日六题-不错题

链接&#xff1a; 剑指 Offer 04. 二维数组中的查找 题意&#xff1a; 一个二维矩阵数组&#xff0c;在行上非递减&#xff0c;列上也非递减 解&#xff1a; 虽然在行列上非递减&#xff0c;但是整体并不有序&#xff0c;第一行存在大于第二行的数字&#xff0c;第一列存在…...

编程日记 2023/8/9 3:09:52

Elasticsearch搜索出现NAN异常

原因分析 Elasticsearch默认的打分&#xff0c;一般是不会出现异常的之所以会出现NAN异常&#xff0c;往往是因为我们重新计算了打分&#xff0c;使用了function_score核心原因是在function_score中&#xff0c;出现了计算异常&#xff0c;比如 0/0,比如log1p(x),x为负数等 真…...

编程日记 2023/8/9 3:08:50

(杭电多校)2023“钉耙编程”中国大学生算法设计超级联赛（6）

1001 Count 当k在区间(1n)/2的左边时,如图,[1,k]和[n-k1,n]完全相同,所以就m^(n-k) 当k在区间(1n)/2的右边时,如图,[1,n-k1]和[k,n]完全相同,所以也是m^(n-k) 别忘了特判,当k等于n时,n-k为0,然后a1a1,a2a2,..anan,所以没什么限制,那么就是m^n AC代码&#xff1a; #includ…...

编程日记 2023/8/9 3:07:47

【JavaScript 】浏览器事件处理

1. 什么是浏览器事件？ 浏览器事件是指在网页中发生的各种交互和动作，例如用户点击按钮、页面加载完成、输入框文本变化等。通过处理这些事件，可以编写相应的JavaScript代码来实现特定的功能和行为。 2. 常见的浏览器事件 以下是一些常见的浏览器事件及其用途的详细介绍： c…...

编程日记 2023/8/9 3:06:46

(力扣)用两个队列实现栈---C语言

分享一首歌曲吧&#xff0c;希望在枯燥的刷题生活中带给你希望和勇气&#xff0c;加油&#xff01; 题目&#xff1a; 请你仅使用两个队列实现一个后入先出&#xff08;LIFO&#xff09;的栈&#xff0c;并支持普通栈的全部四种操作&#xff08;push、top、pop 和 empty&#…...

编程日记 2023/8/9 3:05:45

使用 RediSearch 在 Redis 中进行全文检索

原文链接&#xff1a; 使用 RediSearch 在 Redis 中进行全文检索 Redis 大家肯定都不陌生了&#xff0c;作为一种快速、高性能的键值存储数据库&#xff0c;广泛应用于缓存、队列、会话存储等方面。 然而&#xff0c;Redis 在原生状态下并不支持全文检索功能&#xff0c;这使…...

编程日记 2023/8/9 3:04:44

[Microsoft][ODBC 驱动程序管理器] 未发现数据源名称并且未指定默认驱动程序

1.今天开发了一套服务程序&#xff0c;使用的是Odbc连接MySql数据库&#xff0c; 在我本机用VS打开程序时&#xff0c;访问一切正常&#xff0c;当发布出来装在电脑上&#xff0c;连接数据库时提示&#xff1a; [Microsoft][ODBC 驱动程序管理器] 未发现数据源名称并且未指定…...

编程日记 2023/8/9 3:03:43

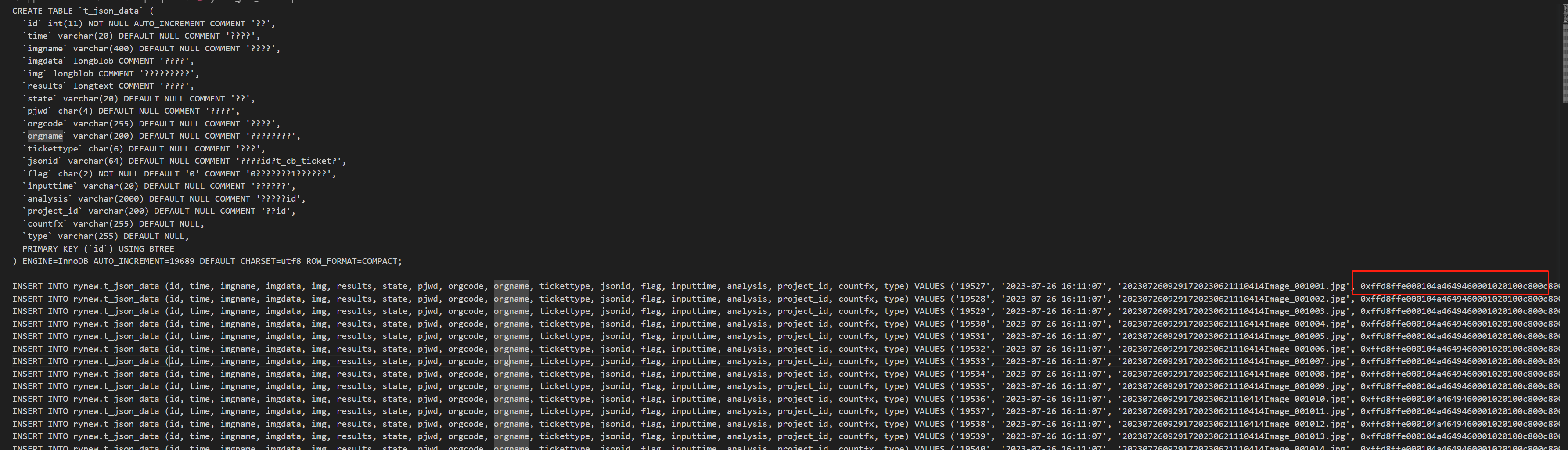
springboot生成表结构和表数据sql

需求 业务背景是需要某单机程序需要把正在进行的任务导出&#xff0c;然后另一台电脑上单机继续运行&#xff0c;我这里选择的方案是同步SQL形式&#xff0c;并保证ID随机&#xff0c;多个数据库不会重复。 实现 package com.nari.web.controller.demo.controller;import cn…...

编程日记 2023/8/9 3:02:42

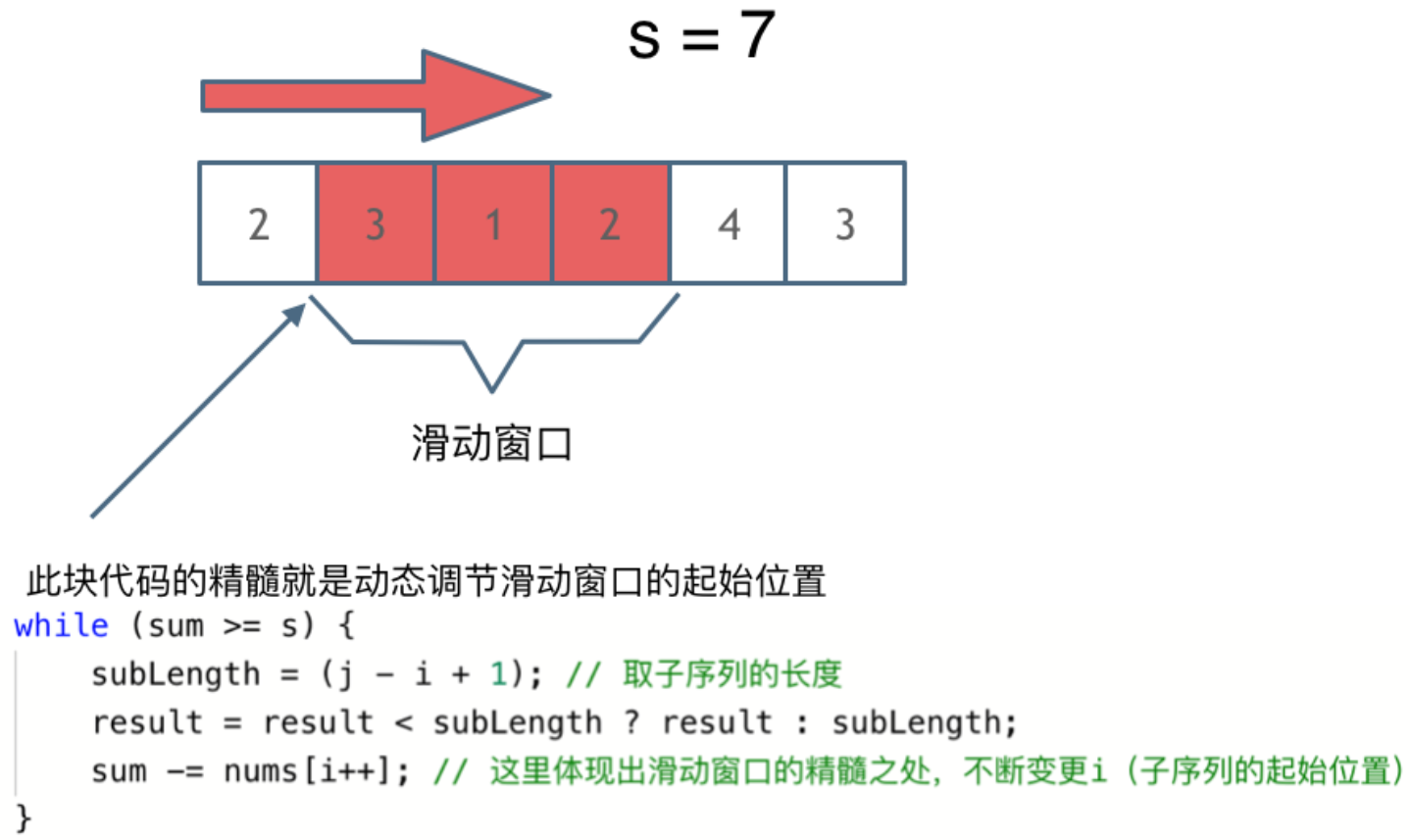
代码随想录—力扣算法题：209长度最小的子数组.Java版（示例代码与导图详解）

版本说明 当前版本号[20230808]。 版本修改说明20230808初版 目录 文章目录 版本说明目录209.长度最小的子数组思路暴力解法滑动窗口 两种方法的区别总结 209.长度最小的子数组 力扣题目链接 更多内容可点击此处跳转到代码随想录&#xff0c;看原版文件 给定一个含有 n 个…...

编程日记 2023/8/9 3:01:41

81 | Python可视化篇 —— Seaborn数据可视化

Seaborn是Python中一个基于Matplotlib的高级数据可视化库，它提供了更简单的API和更美观的图形样式，适用于数据探索和展示。在本教程中，我们将介绍Seaborn的基本概念和用法，并通过一些示例演示如何使用Seaborn来创建各种图表和图形。 文章目录 1. 导入Seaborn库和数据2. 数据…...

编程日记 2023/8/9 3:00:40

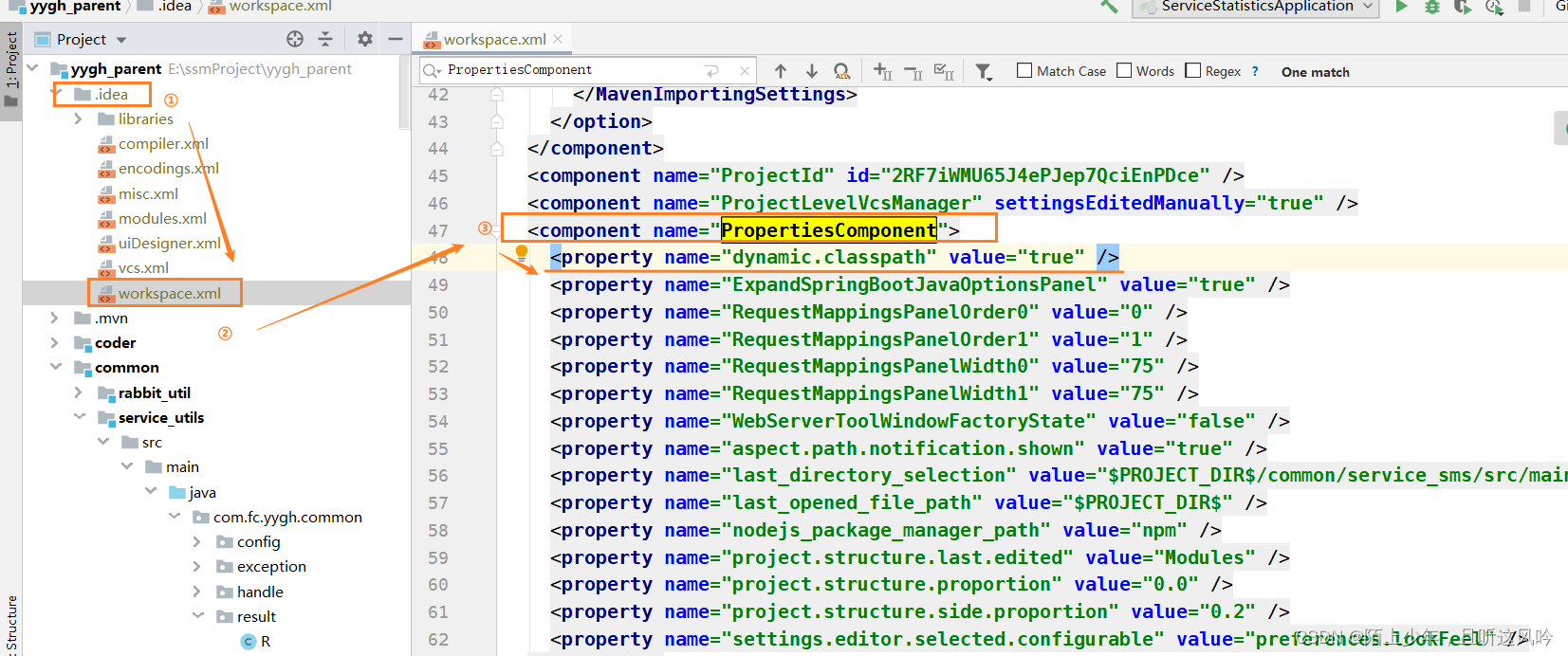
解决Error running XXXApplicationCommand line is too long.报错

测试IDEA版本&#xff1a;2019.2.4 &#xff0c;2020.1.3 文章目录 一. 问题场景二. 报错原因2.1 为什么命令行过长会导致这种问题? 三. 解决方案3.1 方案一3.2 方案二 一. 问题场景 当我们从GitHub或公司自己搭建的git仓库上拉取项目代码时&#xff0c;会出现以下错误 报错代…...

编程日记 2023/8/9 2:59:39

【Linux】—— 进程等待 waitwaitpid

序言&#xff1a; 之前讲过&#xff0c;子进程退出&#xff0c;父进程如果不管不顾&#xff0c;就可能造成‘僵尸进程’的问题&#xff0c;进而造成内存泄漏。因此&#xff0c;为了解决这个问题&#xff0c;就需要用到有关 “进程等待” 的基本知识&#xff01;&#xff01;&am…...

编程日记 2023/8/9 2:58:35

el-tree 懒加载数据，增删改时局部刷新实现

1.数据过多时进行懒加载孩子节点&#xff0c;根据层级传参获取后端孩子数据 懒加载主要部分&#xff1a; 1参数: :load"loadNode" lazy :props"defaultProps" 2.defaultProps 需要设置isLeaf: isLeaf,去除最后一层孩子节点的展开图表 defaultProps: { ch…...

编程日记 2023/8/9 2:57:34

【Axure高保真原型】引导弹窗

今天和大家中分享引导弹窗的原型模板&#xff0c;载入页面后&#xff0c;会显示引导弹窗&#xff0c;适用于引导用户使用页面&#xff0c;点击完成后&#xff0c;会显示下一个引导弹窗&#xff0c;直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

编程新知 2026/2/8 4:37:29

地震勘探——干扰波识别、井中地震时距曲线特点

目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波&#xff1a;可以用来解决所提出的地质任务的波&#xff1b;干扰波&#xff1a;所有妨碍辨认、追踪有效波的其他波。 地震勘探中&#xff0c;有效波和干扰波是相对的。例如&#xff0c;在反射波…...

编程新知 2026/2/8 20:43:05

k8s从入门到放弃之Ingress七层负载

k8s从入门到放弃之Ingress七层负载 在Kubernetes&#xff08;简称K8s&#xff09;中&#xff0c;Ingress是一个API对象&#xff0c;它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress&#xff0c;你可…...

编程新知 2025/9/7 0:12:53

在rocky linux 9.5上在线安装 docker

前面是指南&#xff0c;后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

编程新知 2025/7/27 10:03:12

Docker 运行 Kafka 带 SASL 认证教程

Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明&#xff1a;server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

编程新知 2026/1/23 4:15:03

条件运算符

C中的三目运算符&#xff08;也称条件运算符&#xff0c;英文&#xff1a;ternary operator&#xff09;是一种简洁的条件选择语句&#xff0c;语法如下&#xff1a; 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true&#xff0c;则整个表达式的结果为“表达式1”…...

编程新知 2025/12/6 22:50:48

第25节 Node.js 断言测试

Node.js的assert模块主要用于编写程序的单元测试时使用&#xff0c;通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试&#xff0c;通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

编程新知 2025/10/11 0:24:31

【Web 进阶篇】优雅的接口设计：统一响应、全局异常处理与参数校验

系列回顾&#xff1a; 在上一篇中&#xff0c;我们成功地为应用集成了数据库&#xff0c;并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了&#xff01;但是&#xff0c;如果你仔细审视那些 API&#xff0c;会发现它们还很“粗糙”&#xff1a;有…...

编程新知 2026/1/22 20:46:43

【JavaWeb】Docker项目部署

引言 之前学习了Linux操作系统的常见命令&#xff0c;在Linux上安装软件&#xff0c;以及如何在Linux上部署一个单体项目&#xff0c;大多数同学都会有相同的感受&#xff0c;那就是麻烦。 核心体现在三点&#xff1a; 命令太多了&#xff0c;记不住 软件安装包名字复杂&…...

编程新知 2026/2/4 16:07:02

ABAP设计模式之---“简单设计原则(Simple Design)”

“Simple Design”&#xff08;简单设计&#xff09;是软件开发中的一个重要理念&#xff0c;倡导以最简单的方式实现软件功能&#xff0c;以确保代码清晰易懂、易维护&#xff0c;并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计&#xff0c;遵循“让事情保…...

编程新知 2026/1/27 18:13:23