[机器学习]线性回归模型
线性回归
线性回归:根据数据,确定两种或两种以上变量间相互依赖的定量关系
函数表达式:
y = f ( x 1 , x 2 . . . x n ) y = f(x_1,x_2...x_n) y=f(x1,x2...xn)
回归根据变量数分为一元回归[ y = f ( x ) y=f(x) y=f(x)]和多元回归[ y = f ( x 1 , x 2 . . . x n ) y = f(x_1,x_2...x_n) y=f(x1,x2...xn)],根据函数关系分为线性回归[ y = a x + b y=ax+b y=ax+b]与非线性回归[ y = a x 2 + b x + c y=ax^2+bx+c y=ax2+bx+c]
平方误差成本函数:
m i n i m i z e ( J ) minimize(J) minimize(J)
J = 1 2 m ∑ i = 1 m ( y i ‘ − y i ) 2 = 1 2 m ∑ i = 1 m ( a x i + b − y i ) 2 = g ( a , b ) J=\frac{1}{2m} \sum_{i=1}^{m}(y^{`}_i-y_i)^2=\frac{1}{2m} \sum_{i=1}^{m}(ax_i+b-y_i)^2=g(a,b) J=2m1i=1∑m(yi‘−yi)2=2m1i=1∑m(axi+b−yi)2=g(a,b)
梯度下降算法:
J = f ( p ) J=f(p) J=f(p)
p = p − α ∂ ∂ p i f ( p i ) p = p - \alpha \frac{\partial}{\partial p_i}f(p_i) p=p−α∂pi∂f(pi)
寻找极小值的一种方法。通过向函数上当前点对应梯度(或者是近似梯度)的反方向的规定步长距离点进行迭代搜索,直到在极小点收敛。
实验:
基于generated_data.csv数据,建立线性回归模型,预测x=3.5对应的y值,评估模型表现
#load the data
import pandas as pd
data = pd.read_csv('D:\workspace\data\ML\generated_data.csv')data.head()
print(type(data), data.shape)x = data.loc[:,'x']
y = data.loc[:,'y']
print(x,y)#visualize the data
from matplotlib import pyplot as plt
plt.figure(figsize=(5,5))
plt.scatter(x,y)
plt.show()# set up a linear regression model
from sklearn.linear_model import LinearRegression
lr_model = LinearRegression()import numpy as np
x = np.array(x)
x = x.reshape(-1,1)
y = np.array(y)
y = y.reshape(-1,1)lr_model.fit(x,y)y_predict = lr_model.predict(x)
print(y_predict)print(y)y_predict_single = lr_model.predict([[3.5]])print(y_predict_single)# a/b print
a = lr_model.coef_
b = lr_model.intercept_
print(a,b)from sklearn.metrics import mean_squared_error, r2_score
MSE = mean_squared_error(y, y_predict)
R2 = r2_score(y, y_predict)
print(MSE, R2)plt.figure()
plt.plot(y,y_predict)
plt.show()
运行结果:
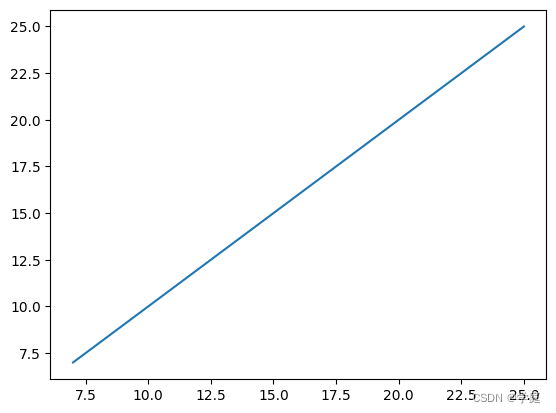
其中MSE为 3.1554436208840474 e − 31 3.1554436208840474e^{-31} 3.1554436208840474e−31,R2为1.0
实验结论:在这个实验中,我们建立了一个单因子线性回归模型,得到x=3.5对应的y值为12,其均方误差(MSE)非常接近于零,而确定系数(R^2)接近于1。这表明我们的模型可以非常好地拟合数据,预测能力非常强。
附:generated_data,csv数据
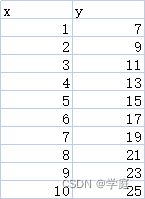
相关文章:

[机器学习]线性回归模型
线性回归 线性回归:根据数据,确定两种或两种以上变量间相互依赖的定量关系 函数表达式: y f ( x 1 , x 2 . . . x n ) y f(x_1,x_2...x_n) yf(x1,x2...xn) 回归根据变量数分为一元回归[ y f ( x ) yf(x) yf(x)]和多元回归[ y …...

Vue基于php医院预约挂号系统_6nrhh
随着信息时代的来临,过去的管理方式缺点逐渐暴露,对过去的医院预约挂号管理方式的缺点进行分析,采取计算机方式构建医院预约挂号系统。本文通过阅读相关文献,研究国内外相关技术,开发并设计一款医院预约挂号系统的构建…...

2023-08-07力扣今日六题-不错题
链接: 剑指 Offer 04. 二维数组中的查找 题意: 一个二维矩阵数组,在行上非递减,列上也非递减 解: 虽然在行列上非递减,但是整体并不有序,第一行存在大于第二行的数字,第一列存在…...

Elasticsearch搜索出现NAN异常
原因分析 Elasticsearch默认的打分,一般是不会出现异常的之所以会出现NAN异常,往往是因为我们重新计算了打分,使用了function_score核心原因是在function_score中,出现了计算异常,比如 0/0,比如log1p(x),x为负数等 真…...

(杭电多校)2023“钉耙编程”中国大学生算法设计超级联赛(6)
1001 Count 当k在区间(1n)/2的左边时,如图,[1,k]和[n-k1,n]完全相同,所以就m^(n-k) 当k在区间(1n)/2的右边时,如图,[1,n-k1]和[k,n]完全相同,所以也是m^(n-k) 别忘了特判,当k等于n时,n-k为0,然后a1a1,a2a2,..anan,所以没什么限制,那么就是m^n AC代码: #includ…...

【JavaScript 】浏览器事件处理
1. 什么是浏览器事件? 浏览器事件是指在网页中发生的各种交互和动作,例如用户点击按钮、页面加载完成、输入框文本变化等。通过处理这些事件,可以编写相应的JavaScript代码来实现特定的功能和行为。 2. 常见的浏览器事件 以下是一些常见的浏览器事件及其用途的详细介绍: c…...

(力扣)用两个队列实现栈---C语言
分享一首歌曲吧,希望在枯燥的刷题生活中带给你希望和勇气,加油! 题目: 请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty&#…...

使用 RediSearch 在 Redis 中进行全文检索
原文链接: 使用 RediSearch 在 Redis 中进行全文检索 Redis 大家肯定都不陌生了,作为一种快速、高性能的键值存储数据库,广泛应用于缓存、队列、会话存储等方面。 然而,Redis 在原生状态下并不支持全文检索功能,这使…...
[Microsoft][ODBC 驱动程序管理器] 未发现数据源名称并且未指定默认驱动程序
1.今天开发了一套服务程序,使用的是Odbc连接MySql数据库, 在我本机用VS打开程序时,访问一切正常,当发布出来装在电脑上,连接数据库时提示: [Microsoft][ODBC 驱动程序管理器] 未发现数据源名称并且未指定…...
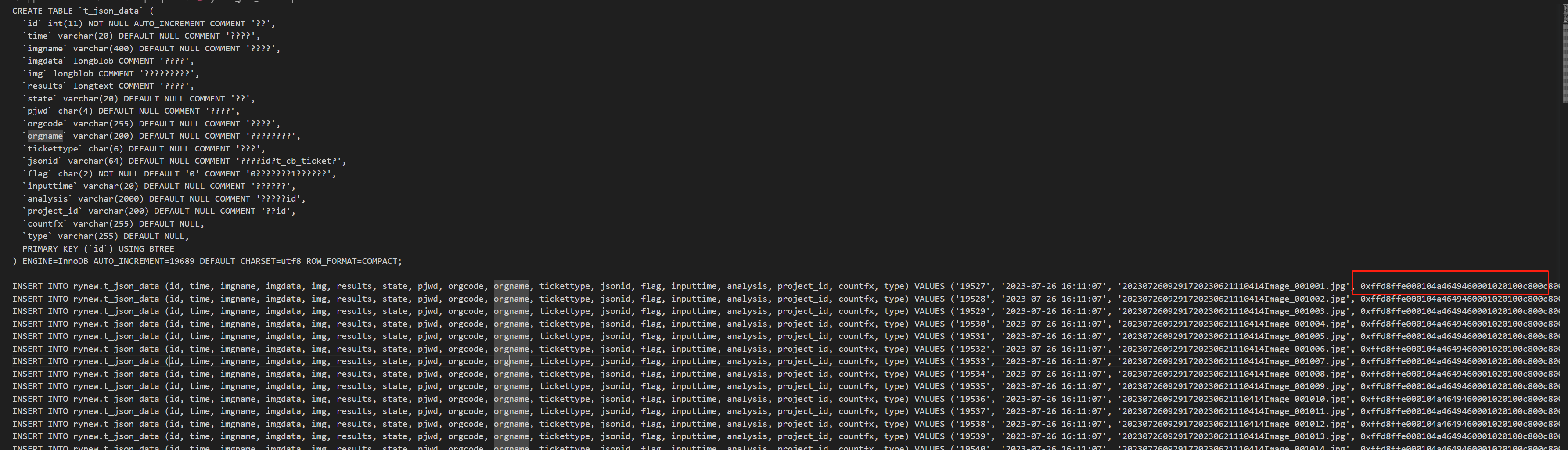
springboot生成表结构和表数据sql
需求 业务背景是需要某单机程序需要把正在进行的任务导出,然后另一台电脑上单机继续运行,我这里选择的方案是同步SQL形式,并保证ID随机,多个数据库不会重复。 实现 package com.nari.web.controller.demo.controller;import cn…...
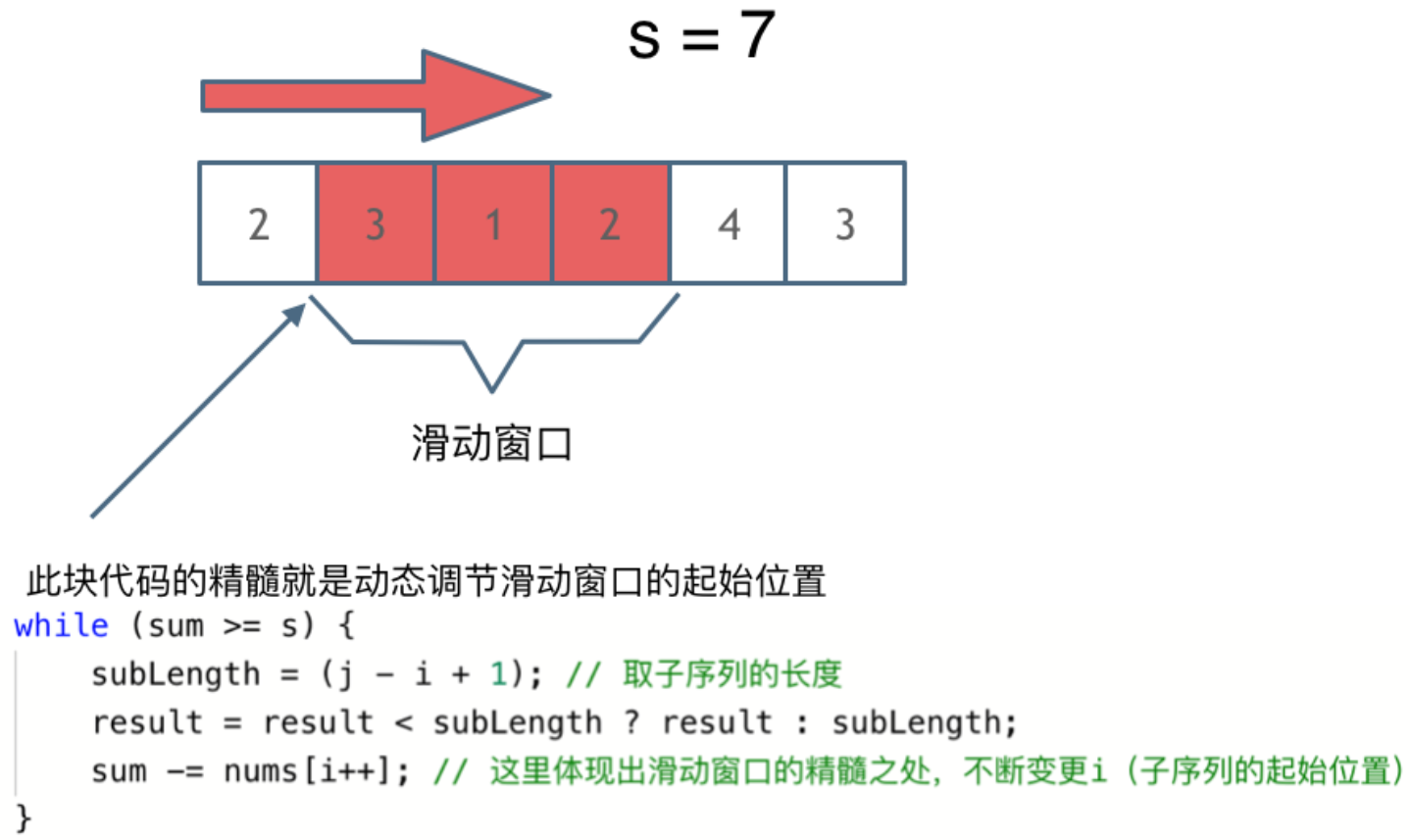
代码随想录—力扣算法题:209长度最小的子数组.Java版(示例代码与导图详解)
版本说明 当前版本号[20230808]。 版本修改说明20230808初版 目录 文章目录 版本说明目录209.长度最小的子数组思路暴力解法滑动窗口 两种方法的区别总结 209.长度最小的子数组 力扣题目链接 更多内容可点击此处跳转到代码随想录,看原版文件 给定一个含有 n 个…...

81 | Python可视化篇 —— Seaborn数据可视化
Seaborn是Python中一个基于Matplotlib的高级数据可视化库,它提供了更简单的API和更美观的图形样式,适用于数据探索和展示。在本教程中,我们将介绍Seaborn的基本概念和用法,并通过一些示例演示如何使用Seaborn来创建各种图表和图形。 文章目录 1. 导入Seaborn库和数据2. 数据…...
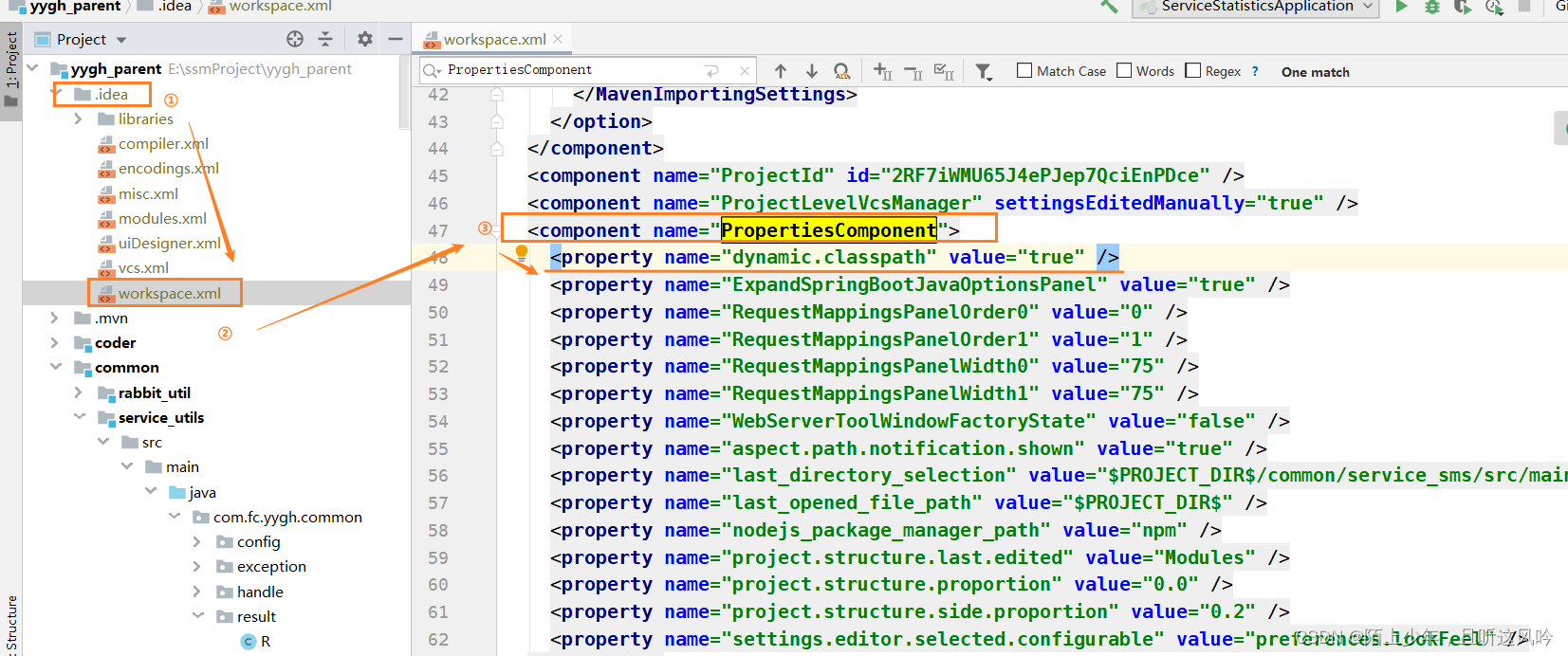
解决Error running XXXApplicationCommand line is too long.报错
测试IDEA版本:2019.2.4 ,2020.1.3 文章目录 一. 问题场景二. 报错原因2.1 为什么命令行过长会导致这种问题? 三. 解决方案3.1 方案一3.2 方案二 一. 问题场景 当我们从GitHub或公司自己搭建的git仓库上拉取项目代码时,会出现以下错误 报错代…...

【Linux】—— 进程等待 waitwaitpid
序言: 之前讲过,子进程退出,父进程如果不管不顾,就可能造成‘僵尸进程’的问题,进而造成内存泄漏。因此,为了解决这个问题,就需要用到有关 “进程等待” 的基本知识!!&am…...

el-tree 懒加载数据,增删改时局部刷新实现
1.数据过多时进行懒加载孩子节点,根据层级传参获取后端孩子数据 懒加载主要部分: 1参数: :load"loadNode" lazy :props"defaultProps" 2.defaultProps 需要设置isLeaf: isLeaf,去除最后一层孩子节点的展开图表 defaultProps: { ch…...
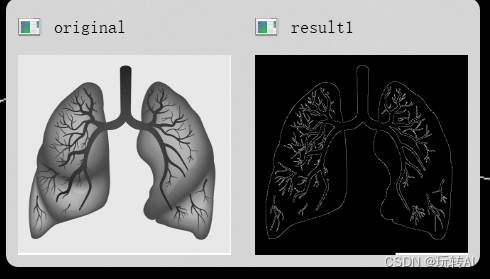
opencv基础44- Canny边缘检测详解-cv.Canny()
什么是Canny边缘检测? Canny边缘检测是一种经典的边缘检测算法,由John F. Canny在1986年提出。它被广泛应用于计算机视觉和图像处理领域,是一种多阶段的边缘检测算法,能够有效地检测图像中的边缘并抑制噪声。 Canny边缘检测的主要…...
--函数)
neo4j查询语言Cypher详解(三)--函数
函数 Cypher中的函数如果输入参数为null,则返回null。 以字符串作为输入的函数都对Unicode字符进行操作,而不是对标准字符进行操作。例如,size()函数应用于任何Unicode字符将返回1,即使该字符不适合一个字符的16位。 可以通过 …...

kafka权威指南(阅读摘录)
零复制 Kafka 使用零复制技术向客户端发送消息——也就是说,Kafka 直接把消息从文件(或者更确切地说是 Linux 文件系统缓存)里发送到网络通道,而不需要经过任何中间缓冲区。这是 Kafka 与其他大部分数据库系统不一样的地方&#…...
【爬虫实践】使用Python从网站抓取数据
一、说明 本周我不得不为客户抓取一个网站。我意识到我做得如此自然和迅速,分享它会很有用,这样你也可以掌握这门艺术。【免责声明:本文展示了我的抓取做法,如果您有更多相关做法请在评论中分享】 二、计划策略 2.1 策划 确定您…...
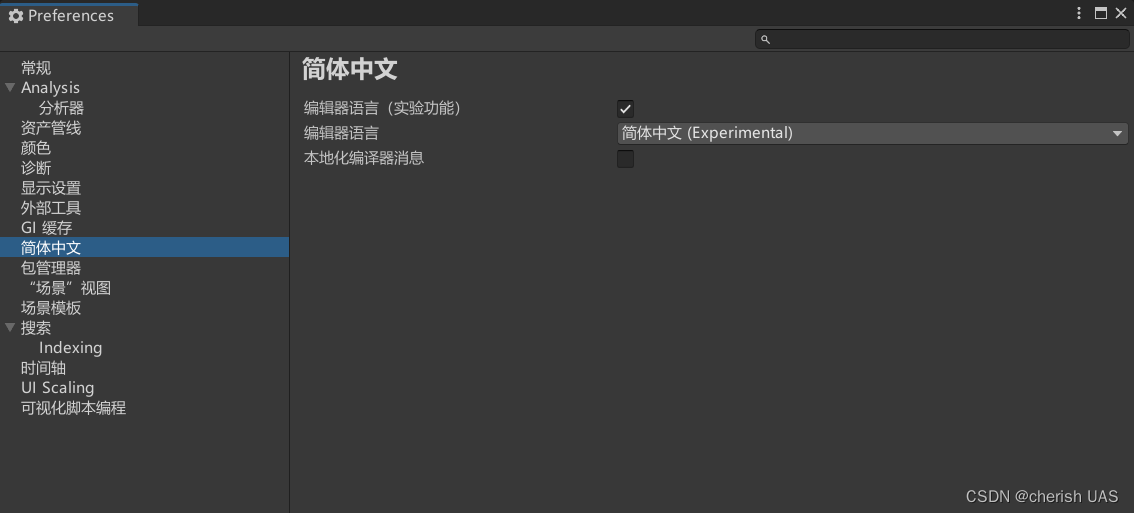
win10 2022unity设置中文
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言解决方法 前言 在Edit->preferences里找不到language选项。 解决方法 【1】打开下面地址 注意 :把{version}换成你当前安装的版本,比如说如果…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...
