剑指Offer13.机器人的运动范围 C++
1、题目描述
- 地上有一个m行n列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动,它每次可以向左、右、上、下移动一格(不能移动到方格外),也不能进入行坐标和列坐标的数位之和大于k的格子。例如,当k为18时,机器人能够进入方格 [35, 37] ,因为3+5+3+7=18。但它不能进入方格 [35, 38],因为3+5+3+8=19。请问该机器人能够到达多少个格子?
- 示例 1:
输入:m = 2, n = 3, k = 1
输出:3 - 示例 2:
输入:m = 3, n = 1, k = 0
输出:1
2、VS2019上运行
使用方法一:广度优先搜索BFS
#include <iostream>
#include <vector>
#include <queue>
using namespace std;class Solution {// 计算 x 的数位之和int get(int x) {int res = 0;for (; x; x /= 10) {res += x % 10;}return res;}
public:int movingCount(int m, int n, int k) {if (!k) return 1;queue<pair<int, int> > Q;//队列Q用于存储待访问的格子数量,第一个表示横坐标,第二个表示纵坐标// 向右和向下的方向数组//以向右(x轴正方向)和向下(y轴正方向)移动为例。int dx[2] = { 0, 1 };int dy[2] = { 1, 0 };//创建一个二维矩阵 vis,用于记录矩阵中每个位置是否已经被访问过。//初始时,所有位置都被标记为未访问(0)。vector<vector<int> > vis(m, vector<int>(n, 0));//m行n列,全部元素设为0//向队列 Q 中插入一个整数对作为元素。这里是将 (0, 0) 作为起始位置插入到队列中Q.push(make_pair(0, 0));vis[0][0] = 1;//将矩阵 vis 中坐标 (0, 0) 的元素设置为 1,表示该位置已被访问。int ans = 1;//变量 ans 用于记录满足特定条件的位置数量while (!Q.empty()) {// 取出队首的格子位置pair<int, int> front = Q.front();Q.pop();//将整数对 front 中的第一个元素和第二个元素分别存储到变量 x 和 y 中。也就是横坐标和纵坐标int x = front.first;int y = front.second;for (int i = 0; i < 2; ++i) {//循环遍历一个长度为2的数组,右和下int tx = dx[i] + x;//计算出下一个横坐标int ty = dy[i] + y;//计算下一个纵坐标// 判断下一个位置是否满足限制条件if (tx < 0 || tx >= m || ty < 0 || ty >= n || vis[tx][ty] || get(tx) + get(ty) > k) continue;Q.push(make_pair(tx, ty));//将计算出的下一个位置 (tx, ty) 插入到队列 Q 中,作为待访问的位置。vis[tx][ty] = 1;//该位置已访问ans++;}}return ans;}
};
int main() {int m = 2, n = 3, k = 1;Solution sol;int result = sol.movingCount(m, n, k);cout << result << endl;return 0;
}
3
3、解题思路
- 这段代码是解决一个问题:给定一个 m × n 的矩阵,矩阵中的每个位置代表一个格子。现在有一个机器人位于矩阵的左上角,机器人可以向右或向下移动,但不能移动到数位之和大于 k 的格子。请问,机器人能够到达多少个格子?
具体的解决思路如下: - 1.定义一个函数 get(int x),用来计算数位之和。该函数通过循环将数字 x 每一位上的数字相加,返回数位之和。
- 2.在 movingCount 函数中,首先判断特殊情况,如果 k 为 0,表示没有限制,机器人可以到达任意位置,所以直接返回 1。
- 3.创建一个队列 Q,用于存储待访问的格子位置。队列中的每个元素都是一个整数对,表示格子的横坐标和纵坐标。
- 4.创建两个方向数组 dx 和 dy,用来表示向右和向下移动的偏移量。
- 5.创建一个二维矩阵 vis,用于记录矩阵中的每个位置是否已经被访问过。初始时,所有位置都被标记为未访问(0)。
- 6.将起始位置 (0, 0) 插入到队列 Q 中,并将矩阵 vis 中对应的位置设为已访问(1)。
- 7.定义变量 ans,初始值为 1,用于记录满足限制条件的位置数量。
- 8.使用广度优先搜索算法,不断遍历队列 Q 中的格子位置,进行下一步移动的判断。
- 9.在遍历的过程中,取出队列头部的格子位置,并将其分别存储到变量 x 和 y 中。
- 10.循环遍历方向数组 dx 和 dy 中的元素,分别计算出下一个位置的横坐标 tx 和纵坐标 ty。
- 11.判断下一个位置是否越界、已经访问过、或数位之和大于 k。如果满足其中任一条件,跳过当前循环,进行下一次循环。
- 12.如果下一个位置满足限制条件,将其插入队列 Q 中作为待访问的位置,并将矩阵 vis 中对应的位置设为已访问(1)。
- 13.将计数器 ans 递增,表示发现了一个满足条件的位置。
- 14.当队列 Q 中的格子位置全部遍历完毕时,返回 ans,即满足条件的位置数量。
- 整体思路是通过广度优先搜索算法遍历满足条件的位置,并使用一个队列和一个二维矩阵分别记录待访问的位置和已访问的位置。算法的时间复杂度为 O(m * n),其中 m 和 n 分别表示矩阵的行数和列数。
4、get函数
// 计算 x 的数位之和int get(int x) {int res = 0;for (; x; x /= 10) {res += x % 10;}return res;}
- 这段代码定义了一个名为 get 的函数,它的作用是计算一个整数 x 的数位之和。
- 首先,变量 res 被初始化为 0,用于保存数位之和的结果。
- 然后,通过一个 for 循环,循环的条件是 x 不为0,循环体内执行 x = x / 10,即将 x 除以 10,这样可以实现依次取 x 的个位、十位、百位等。
- 在每次循环中,通过 x % 10 取出 x 的个位数,然后将它加到 res 变量上。
- 最后,当循环结束时,函数返回 res,即计算得到的数位之和。
- 例如,如果 x 的值为 12345,那么这个函数将返回的数位之和为 1 + 2 + 3 + 4 + 5 = 15。
5、queue<pair<int, int> > Q
- 这行代码声明了一个名为 Q 的队列变量,用于存储格子的位置信息。
- Q 是一个队列,每个队列元素都是一个二维坐标的整数对,表示矩阵中的某个格子的位置。
- pair<int, int> 表示一个这样的二维坐标对,其中第一个整数表示横坐标,第二个整数表示纵坐标。
- 这样定义的队列 Q 可以用来保存待访问的格子位置,通常在广度优先搜索算法中会使用队列来实现。通过队列的先进先出特性,可以实现按照一定顺序逐步处理格子位置,从而完成搜索或遍历操作。
6、 vector<vector > vis(m, vector(n, 0));
- 这行代码声明了一个二维矩阵变量 vis,用于记录矩阵中每个位置的访问状态。
- vis 是一个二维的 vector,其中第一维表示矩阵的行数 m,第二维表示矩阵的列数 n。这样定义的二维矩阵 vis 有 m 行、n 列。
- vector<int>(n, 0) ,为每一行创建一个内部向量,创建一个包含 n 个元素的整数型向量,并将每个元素的初始值设置为0。这样创建的向量将被用作矩阵 vis 的每一行,用于表示对应位置的访问状态。
- 在 vector<int>(n, 0) 中,vector<int> 表示创建一个整数型向量,(n, 0) 是一个构造函数的参数,指定了向量的大小为 n,且将每个元素初始化为0。最终得到的向量将作为矩阵 vis 的一行。
- 在该算法中,vis 矩阵用于记录矩阵中每个位置的访问状态。当一个位置被访问时,对应位置的值会被设置为1,表示已经访问过。这在广度优先搜索等算法中很常见,可以避免重复访问同一个位置。
7、for (int i = 0; i < 2; ++i) {};
- 循环遍历一个长度为2的数组是为了考虑当前位置 (x, y) 的相邻位置。
- 在给定的代码中,循环遍历的是长度为2的数组 [0, 1]。这是因为在二维矩阵中,我们通常只需要考虑横向和纵向的相邻位置,即上方、下方、左侧和右侧位置。这个数组的两个元素 [0, 1] 分别表示在横向和纵向上的移动方式。
相关文章:

剑指Offer13.机器人的运动范围 C++
1、题目描述 地上有一个m行n列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动,它每次可以向左、右、上、下移动一格(不能移动到方格外),也不能进入行坐标和列坐标的数位之和大于k的…...

List、Map、Set打印
List List:和数组类似,List可以动态增长,查找元素效率高,插入删除元素效率低,因为会引起其他元素位置改变。 普通[1,2] 1.循环 2.System.out.println(list); int数组[1,2,3,4,5,6,1,2,3] 1.for (int[] array : list)…...

软件机器人在渔业船员证书核发中自动化二次审批制证,提高效率和准确性
近年来,随着科技的不断进步,自动化软件机器人在各个领域得到了广泛应用。在渔业船员证书核发事项中,传统的审批和制证流程相对繁琐。博为小帮软件机器人可以让这一流程变得更加高效和准确。 在过去,渔业船员证书核发事项需要在省级…...
Godot4 C# vscode开发环境搭建
用vscode搭建Godot4 C# 开发环境搭建 软件Godot配置vscode配置结果参考 软件 Godot .Net版本: 下载链接vscode :自行下载.netcore7:.netcore6可能也行vscode插件: Godot配置 1.配置文件用VSCode打开 2.生成C#项目 项目–>工具–>C#->Creat…...
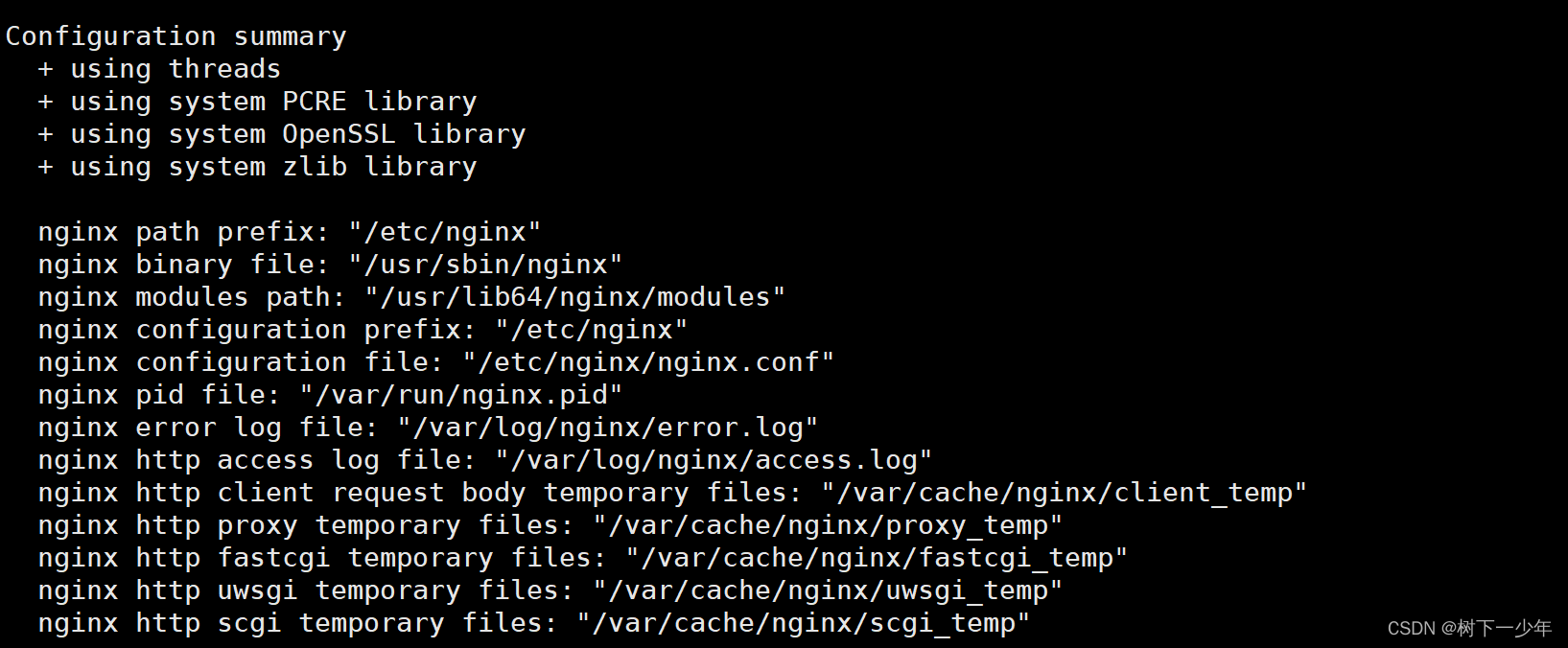
nginx简介与安装配置,目录结构和配置文件介绍
一.nginx简介 1.简介 2.特性 二.nginx安装 1.rpm包方式 (1)下载扩展源 (2)安装扩展rpm包,nginx -V查看配置参数,后面源码安装时要用到 2.源码方式 (1)建议提前下好所需要的部…...
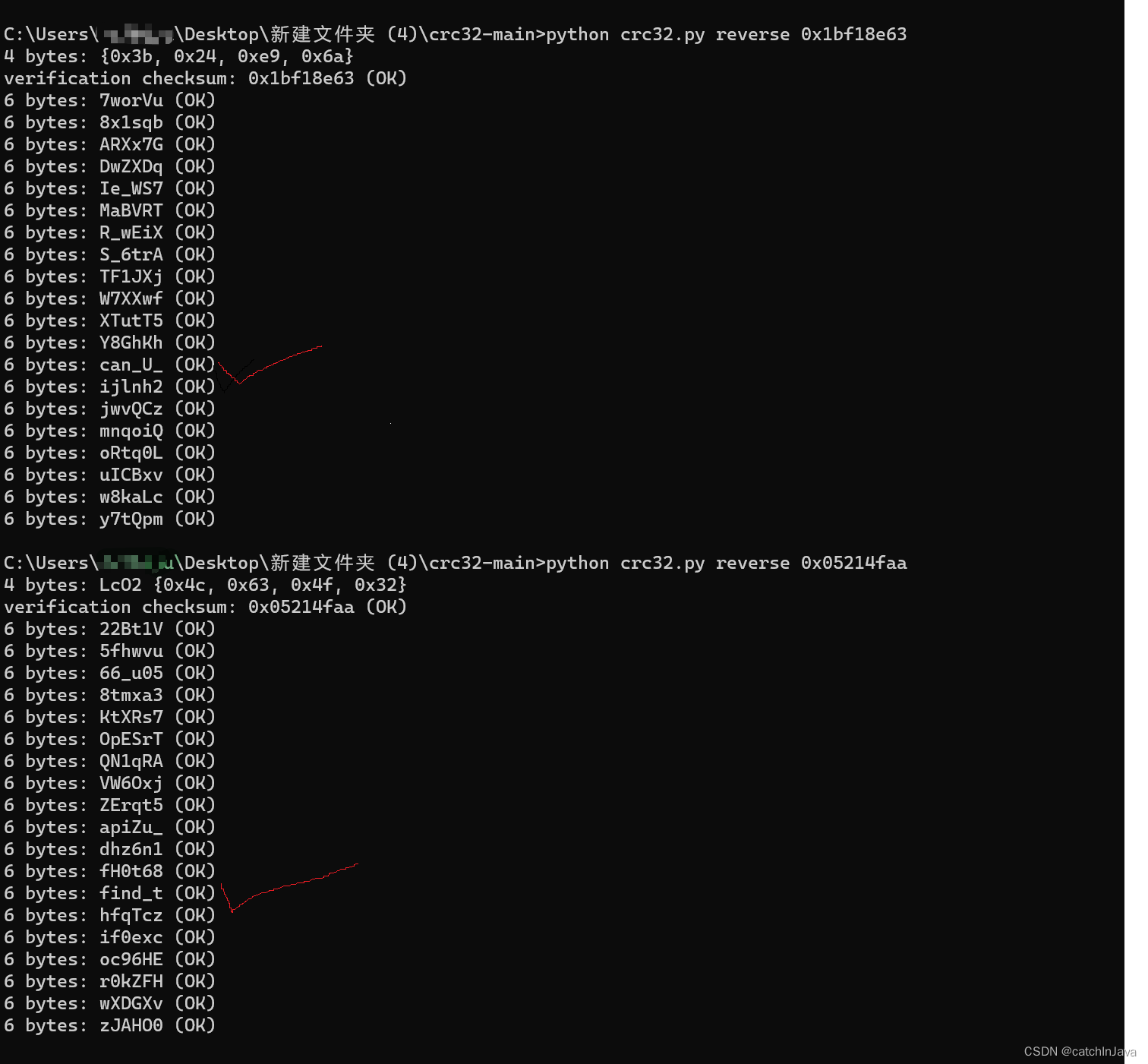
CTF流量题解http4.pcapng
流量分析 导出http 打开报错 验证文件头,发现是zip。 图常片见里文可件能的包16含进:压制缩头包部,word,pdf JPG FF D8 FF E0/FF D8 FF E1 PNG 89 50 4E 47 GIF 47 49 46 38 ZIP 50 4B 03 04 RAR 52 61 72 21 MP3 49 44 33 0 改后缀 使用工具爆破。 git clone git…...

旷视科技AIoT软硬一体化走向深处,生态和大模型成为“两翼”?
齐奏AI交响曲的当下,赛道玩家各自精彩。其中,被称作AI四小龙的商汤科技、云从科技、依图科技、旷视科技已成长为业内标杆,并积极追赶新浪潮。无论是涌向二级市场还是布局最新风口大模型,AI四小龙谁都不甘其后。 以深耕AIoT软硬一…...

STM32 F103C8T6学习笔记2:GPIO的认识—GPIO的基本输入输出—点亮一个LED
今日继续学习使用 STM32 F103C8T6开发板 点亮一个LED灯,文章提供源码,测试工程,实验效果图,希望我的归纳总结会对大家有帮助~ 目录 GPIO的认识与分类 : 引脚安排整理: 定时器的引脚例举: …...

数组相关练习
数组练习 将数组转化成字符串数组拷贝求数组元素的平均值查找数组中指定元素(顺序查找)二分查找冒泡排序数组逆序 将数组转化成字符串 import java.util.Arrays;public class Text1 {public static void main(String[] args) {int[] arr {5, 6, 4, 2};System.out.println(Arr…...

Leetcode-每日一题【剑指 Offer 11. 旋转数组的最小数字】
题目 把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。 给你一个可能存在 重复 元素值的数组 numbers ,它原来是一个升序排列的数组,并按上述情形进行了一次旋转。请返回旋转数组的最小元素。例如,数组 [3,4…...
git教程(第一次使用)
一、gitee和github区别 二、git使用 下载地址 windows:https://gitforwindows.org/ mac:http://sourceforge.net/projects/git-osx-installer/ 1.git初次运行前的配置 (1)配置用户信息 git config --global user.name "…...
Autoware.ai1.14.0自动驾驶-Demo运行
Autoware.ai1.14.0自动驾驶-Demo运行 数据准备 下载数据: wget https://autoware-ai.s3.us-east-2.amazonaws.com/sample_moriyama_data.tar.gz wget https://autoware-ai.s3.us-east-2.amazonaws.com/sample_moriyama_150324.tar.gz一定要注意解压文件是在.auto…...

AttributeConverter
AttributeConverter 是 JPA 中的一个接口,,用于实体属性和 数据库字段,,之间的转换,,,类似mybatis中的typeHandler AttributeConverter使用 定义一个类实现AttributeConverter接口,…...
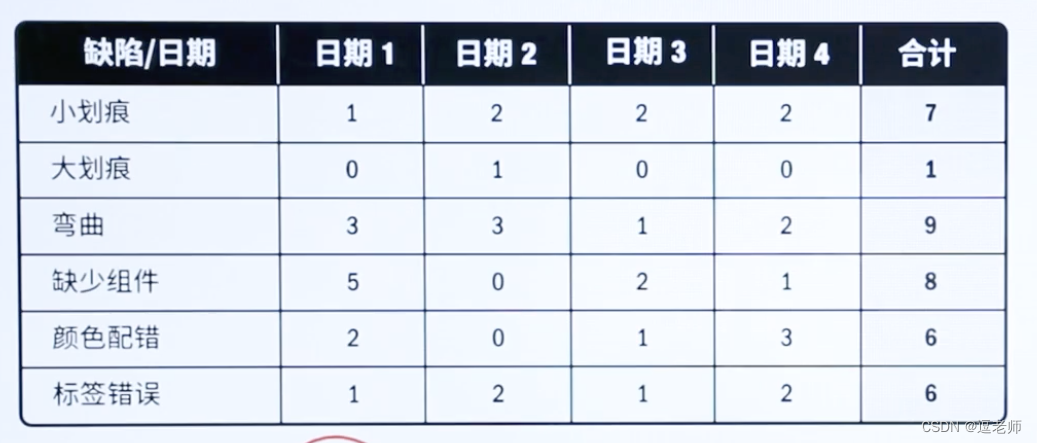
【逗老师的PMP学习笔记】8、项目质量管理
目录 一、规划质量管理1、质量管理的发展历史2、戴明环,PDCA理论3、【关键输入】事业环境因素4、【关键输入】成本效益分析5、【关键工具】质量成本6、【关键输出】质量管理计划7、插一嘴,项目的三个标准8、【关键工具】质量测量指标 二、管理质量1、【关…...
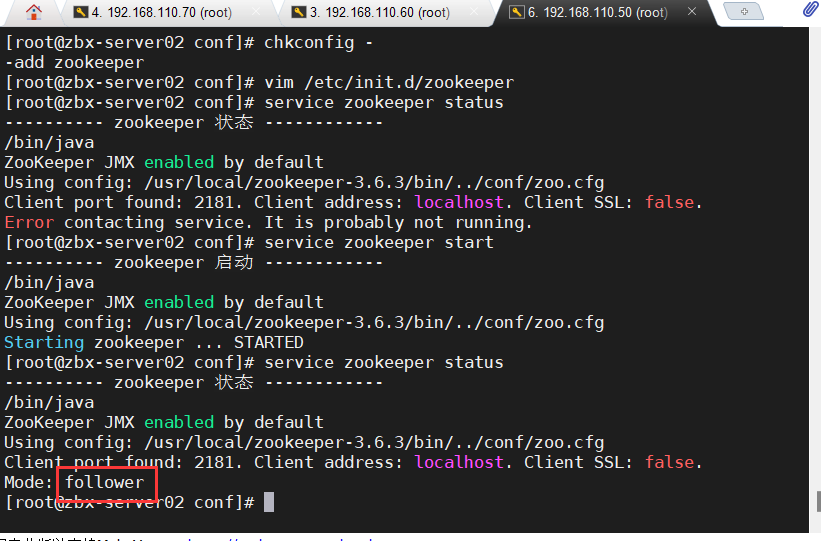
Zookeeper集群
目录 一、Zookeeper 概述 1)Zookeeper 定义 2)Zookeeper 工作机制 3)Zookeeper 特点 4)Zookeeper 数据结构 5)Zookeeper 应用场景 6)Zookeeper 选举机制 ●第一次启动选举机制 ●非第一次启动选举机…...

后端进阶之路——Spring Security构建强大的身份验证和授权系统(四)
前言 「作者主页」:雪碧有白泡泡 「个人网站」:雪碧的个人网站 「推荐专栏」: ★java一站式服务 ★ ★前端炫酷代码分享 ★ ★ uniapp-从构建到提升★ ★ 从0到英雄,vue成神之路★ ★ 解决算法,一个专栏就够了★ ★ 架…...
)
【香瓜说职场】第10月(2018.01.29)
自从17年4月份开始辞职创业,已经10个月了。聊聊近况。 一、博客被冻结 冻结原因是我把博客的积分放在淘宝店铺售卖,卖一周就被查了。 我的每个积分售卖0.5元,是全网最低,每个资源下载一般需要2、3个积分。售…...

LeetCode解法汇总1749. 任意子数组和的绝对值的最大值
目录链接: 力扣编程题-解法汇总_分享记录-CSDN博客 GitHub同步刷题项目: https://github.com/September26/java-algorithms 原题链接:力扣 描述: 给你一个整数数组 nums 。一个子数组 [numsl, numsl1, ..., numsr-1, numsr] 的…...
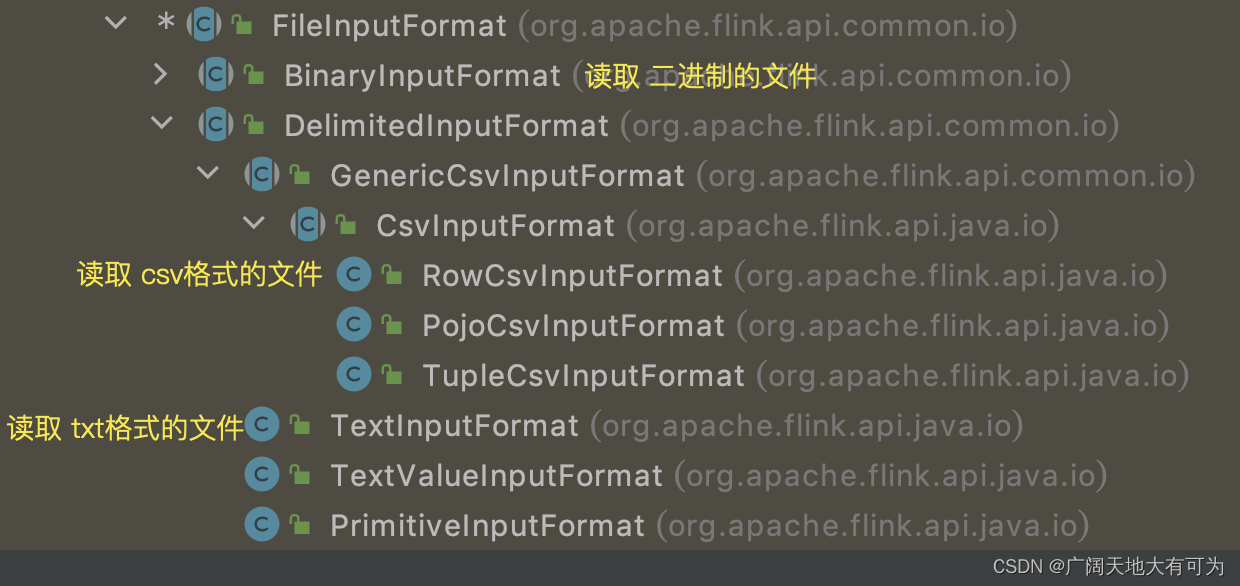
4.2、Flink任务怎样读取文件中的数据
目录 1、前言 2、readTextFile(已过时,不推荐使用) 3、readFile(已过时,不推荐使用) 4、fromSource(FileSource) 推荐使用 1、前言 思考: 读取文件时可以设置哪些规则呢? 1. 文件的格式(tx…...

Effective Java笔记(28)列表优于数组
数组与泛型相比,有两个重要的不同点 。 首先,数组是协变的( covariant ) 。 这个词听起来有点吓人,其实只是表示如果 Sub 为 Super 的子类型,那么数组类型 Sub[ ]就是Super[ ]的子类型。 相反,泛…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...
