jmx prometheus引起的一次cpu飙高
用户接入了jmx agent进行prometheus监控后，在某个时间点出现cpu飙高
排查思路：
1、top，找到java进程ID
2、top -Hp 进程ID，找到java进程下占用高CPU的线程ID
3、jstack 进程ID，找到那个高CPU的线程ID的堆栈。
4、分析堆栈信息
通过排查思路，找到了是jmx prometheus的线程：
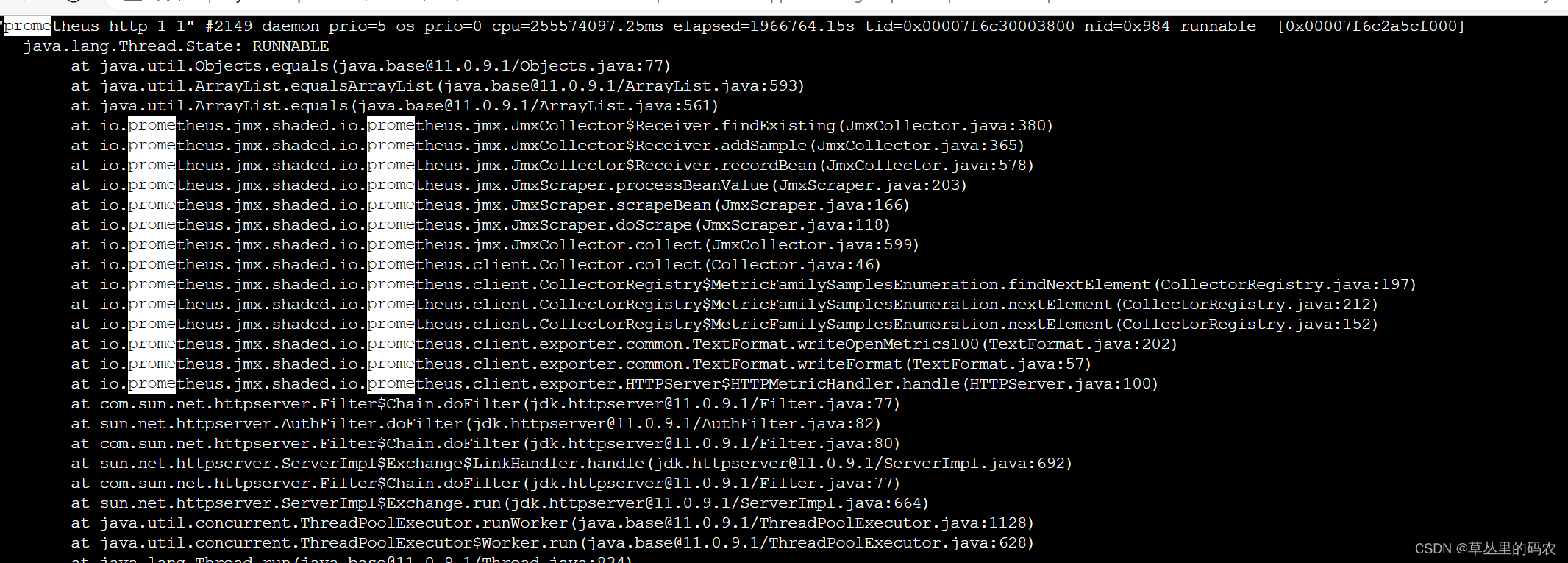
jmx prometheus的源码：
这里只有for循环，很简单的逻辑，所以我们在思考会不会数据量太多了。
通过arthas查看方法返回数据：
watch io.prometheus.jmx.$ findExisting ‘{params,returnObj,throwExp}’ -n 5 -x 3
查看meban数据大小
prometheus 数据：kafka的客户端id一直在变，所以猜想是不是数据量越大prometheus就会越大
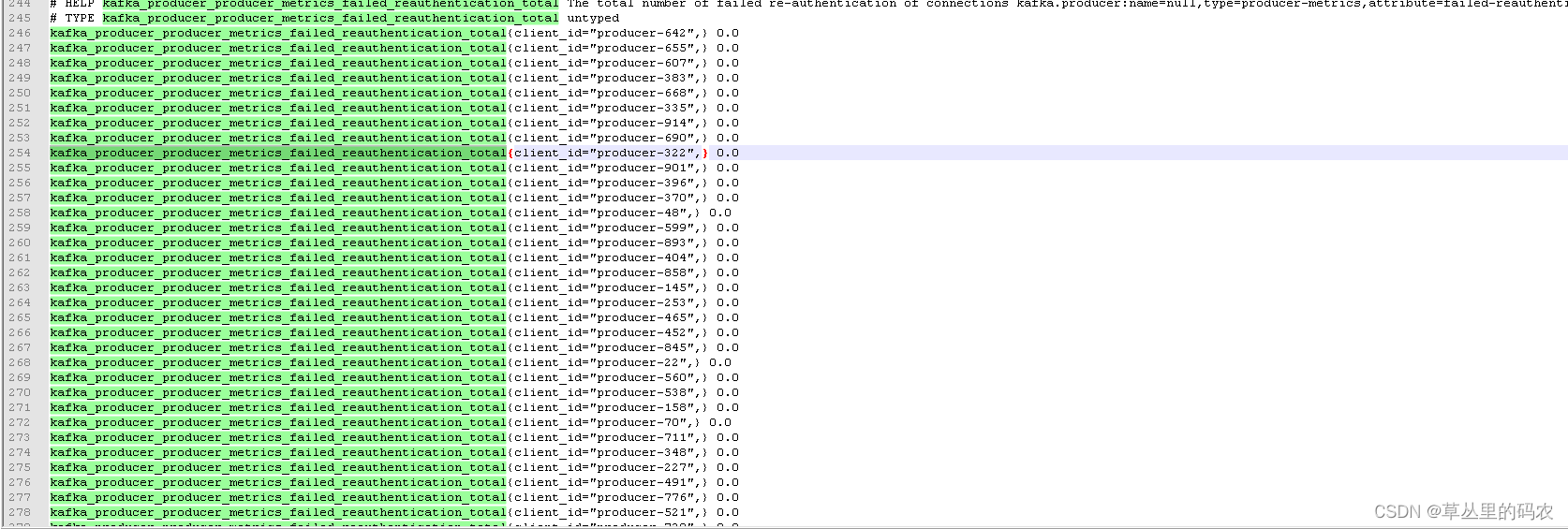
结论：kafaka 消费数据量比较大的时候，jmx 数据就会比较大。jmx prometheus默认的逻辑是会读取全部的java mbean然后转换成prometheus 数据格式，mbean数据比较多的时候，循环就会比较多，cpu计算就会飙高。mbean中的数据有业务客户端的添加进去的，它的数据量是不可控的。
解决方案： 不读取所有的mbean数据，只读取指定的数据格式
相关文章：
jmx prometheus引起的一次cpu飙高
用户接入了jmx agent进行prometheus监控后，在某个时间点出现cpu飙高 排查思路： 1、top，找到java进程ID 2、top -Hp 进程ID，找到java进程下占用高CPU的线程ID 3、jstack 进程ID，找到那个高CPU的线程ID的堆栈。 4、分析堆…...
 SnapshotManager 之状态数据)
Android 虚拟 A/B 详解(六) SnapshotManager 之状态数据
本文为洛奇看世界(guyongqiangx)原创，转载请注明出处。 原文链接：https://blog.csdn.net/guyongqiangx/article/details/129094203 Android 虚拟 A/B 分区《AAndroid 虚拟 A/B 分区》系列，更新中，文章列表： Android 虚拟分区详解(一) 参考资料推荐Android 虚拟分区详解(二…...
Python快速入门系列之一：Python对象
Python对象1. 列表（list）2. 元组（tuple）3. 字典（dict）4. 集合（set）5. 字符串（string）6. BIF （Built-in Function）7. 列表、集合以及字…...
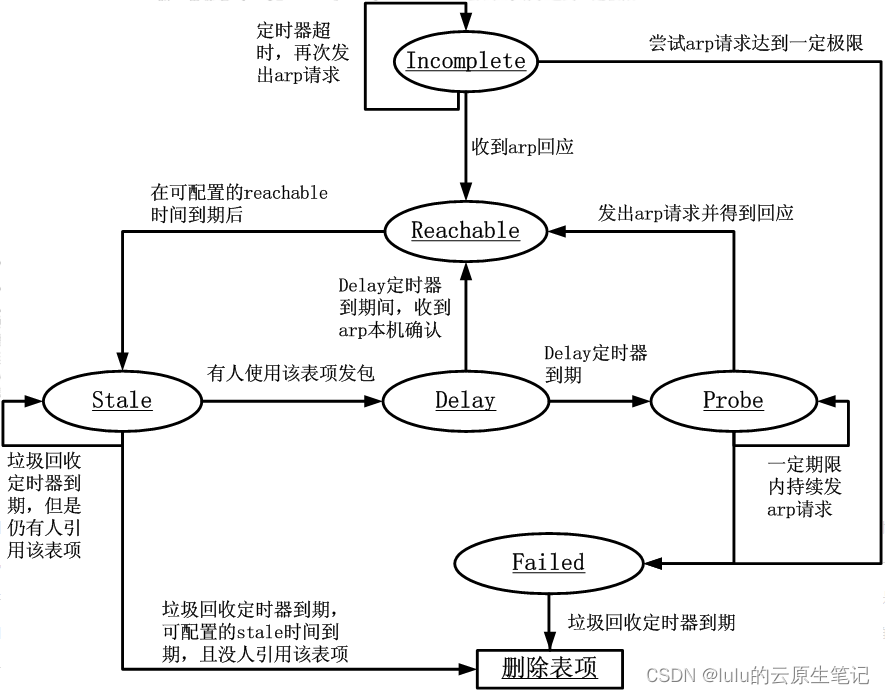
【博客626】不同类型的ARP报文作用以及ARP老化机制
不同类型的ARP报文作用以及ARP老化机制 1、ARP协议及报文 2、不同类型的ARP报文作用 3、ARP工作原理 4、ARP老化机制 5、Linux ARP老化机制 ARP状态机： 在上图中，我们看到只有arp缓存项的reachable状态对于外发包是可用的，对于stale状态的…...
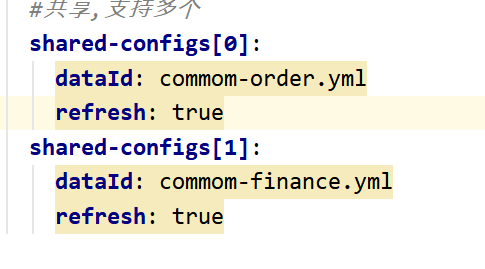
nacos discovery和config
微服务和nacos版本都在2.x及之后。1、discovery用于服务注册，将想要注册的服务注册到nacos中，被naocs发现。pom引入的依赖是：yml配置文件中：2、config用于获取nacos配置管理->配置列表下配置文件中的内容pom引入的依赖是&#…...
【算法数据结构体系篇class06】：堆、大根堆、小根堆、优先队列
一、堆结构1）堆结构就是用数组实现的完全二叉树结构2）完全二叉树中如果每棵子树的最大值都在顶部就是大根堆3）完全二叉树中如果每棵子树的最小值都在顶部就是小根堆4）堆结构的heapInsert与heapify操作5）堆结构的增大ad…...
试题 算法提高 最小字符串
资源限制内存限制：256.0MB C/C时间限制：2.0s Java时间限制：6.0s Python时间限制：10.0s问题描述给定一些字符串(只包含小写字母)，要求将他们串起来构成一个字典序最小的字符串。输入格式第一行T,表示有T组数据。接下来T…...
已解决ImportError: cannot import name ‘featureextractor‘ from ‘radiomics‘
已解决from radiomics import featureextractor导包，抛出ImportError: cannot import name ‘featureextractor‘ from ‘radiomics‘异常的正确解决方法，亲测有效！！！ 文章目录报错问题报错翻译报错原因解决方法联系博…...
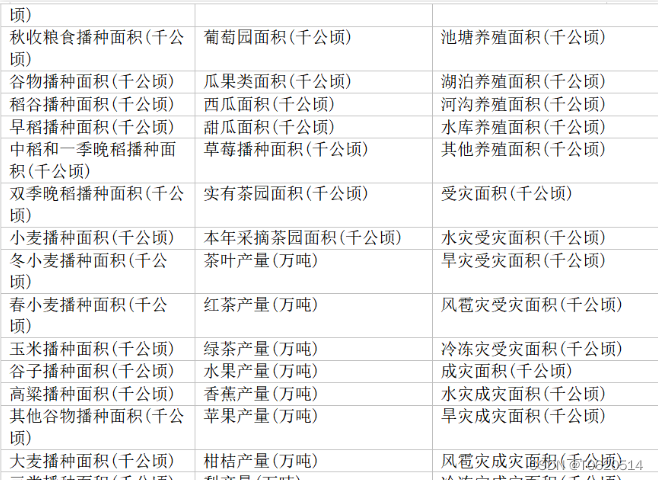
乡村振兴研究：全网最全指标农村经济面板数据（2000-2021年）
数据来源：国家统计局 时间跨度：2000-2021年 区域范围：全国31省 指标说明： 部分样例数据： 行政区划代码地区年份经度纬度乡镇数(个)乡数(个)镇数(个)村民委员会数(个)乡村户数(万户)乡村人口(万人)乡村从业人员(万人…...
C语言中用rand()函数产生一随机数
在C语言中如何产生一个随机数呢？用rand()函数。 rand()函数在头文件：#include <stdio.h>中，函数原型：int rand(void);。rand()会返回一个范围在0到RAND_MAX（32767）之间的随机数（整数&…...
关于系统架构
1.系统架构分类: C/S架构 B/S架构 2.C/S架构 Client / Server（客户端 / 服务器） 特点：需要安装特定的客户端软件。 C/S架构的系统优点和缺点: 优点： 1)速度快(软件中数据大部分都是集成到客户端当中，很少量的数据从服…...
LeetCode 1237. 找出给定方程的正整数解
原题链接 难度：middle\color{orange}{middle}middle 2023/2/18 每日一题 题目描述 给你一个函数 f(x,y)f(x, y)f(x,y) 和一个目标结果 zzz，函数公式未知，请你计算方程 f(x,y)zf(x,y) zf(x,y)z 所有可能的正整数 数对 xxx 和 yyy。满足条件…...
【ArcGIS Pro二次开发】(5)：UI管理_自定义控件的位置
新增的自定义控件一般放在默认的【加载项】选项卡下，但是根据需求，我们可能需要将控件放在新的自定义选项卡下，在自定义选项卡添加系统自带的控件，将自定义的按钮等控件放在右键菜单栏里以方便使用，等等。 下面就以一…...
学习OpenGL图形2D/3D编程
环境：WindowsVisual Studio 2019最流行的几个库：GLUT，SDL，SFML和GLFWGLFWGLAD库查看显卡OPENGL支持情况VS2019glfwgladopenGL3.3顶点着色器片段着色器VAO-VBO-(EBO)->渲染VAO-VBO-EBO->texture纹理矩阵matrix对图形transfor…...
2023美赛思路 | A题时间序列预测任务的模型选择总结
2023美赛思路 | A题时间序列预测任务的模型选择总结 目录 2023美赛思路 | A题时间序列预测任务的模型选择总结基本介绍数据描述任务介绍时序模型基本介绍 这道题分析植被就行，主要涉及不同植被间的相互作用，有竞争有相互促进，我查了下“植物科学数据中心”和“中国迁地保护植…...
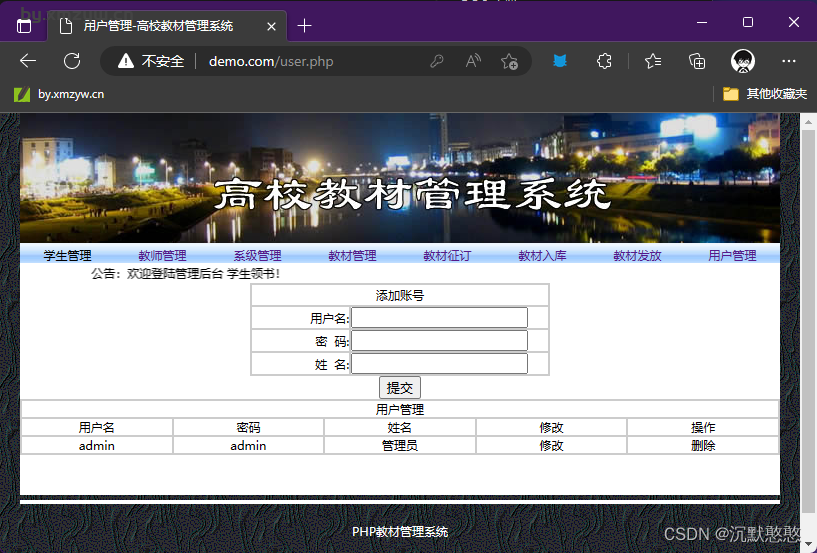
PHP教材管理系统设计（源代码+毕业论文）
【P003】PHP教材管理系统设计（源代码论文） 设计方案 本系统采用B/S结构，所有的程序及数据都放在服务器上，终端在取得相应的权限后使用Web页面浏览，录入，修改等功能。在语言方面使用PHP语言，在…...
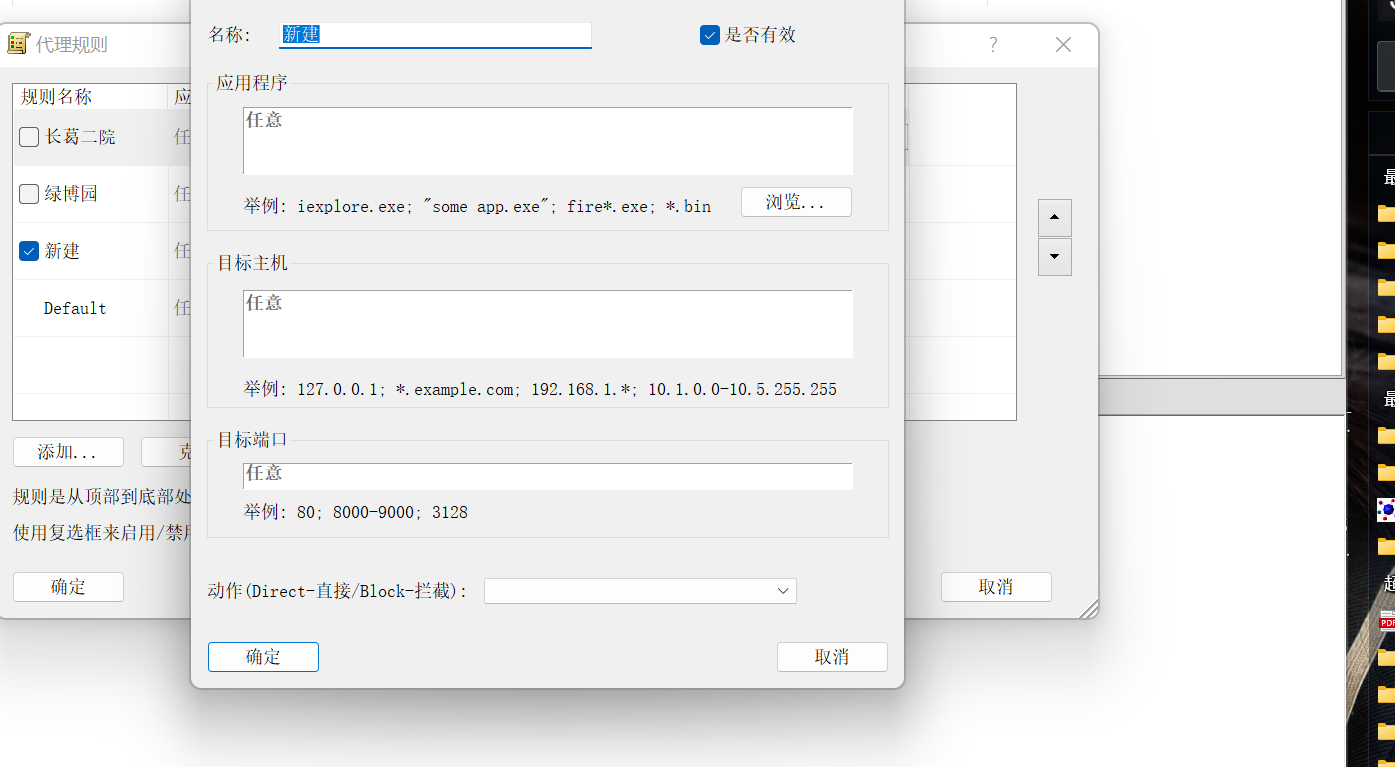
nps内网穿透工具
一、准备一台有公网ip的服务器 https://github.com/ehang-io/nps/releases 在这个地址下载服务端的安装包，centos的下载这个 上传到服务器上。 二、然后解压，安装，启动 [rootadministrator ~]# tar xzvf linux_amd64_server.tar.gz [roo…...
webpack打包时的热模块替代配置以及source-map
1.HMR 在devServer当中添加hot:true 热模块化功能 含义:当其中有一个文件发生变化的时候，那么就会被重新打包一次，极大的提高了构建速度 A.样式文件:可以使用HMR功能，因为在style-loader当中实现了 B.js文件:默认不能使用HMR功能…...
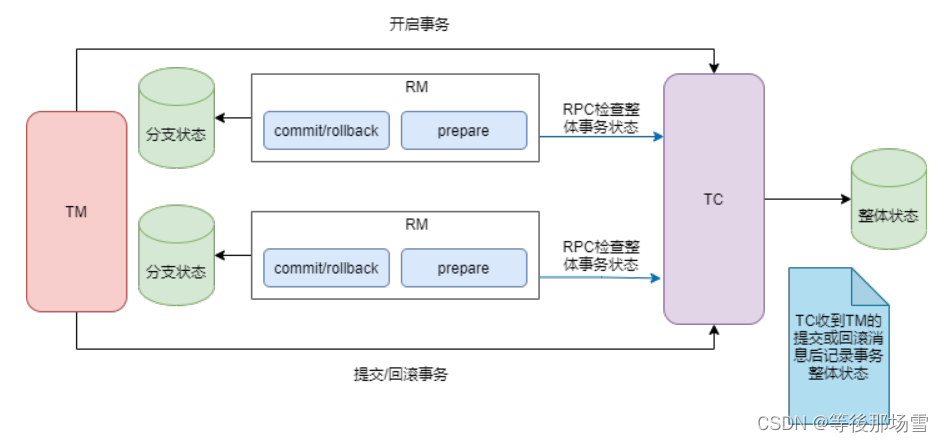
Seata架构篇 - TCC模式
TCC 模式 概述 TCC 是分布式事务中的两阶段提交协议，它的全称为 Try-Confirm-Cancel，即资源预留（Try）、确认操作（Confirm）、取消操作（Cancel）。Try：对业务资源的检查并…...
前端最全面试题整理
前端基础 一、 HTTP/HTML/浏览器 1、说一下 http 和 https https 的 SSL 加密是在传输层实现的。 (1) http 和 https 的基本概念 http: 超文本传输协议，是互联网上应用最为广泛的一种网络协议，是一个客户端和服务器端请求和应答的标准（T…...
浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API，用于在函数组件中使用 state 和其他 React 特性（例如生命周期方法、context 等）。Hooks 通过简洁的函数接口，解决了状态与 UI 的高度解耦，通过函数式编程范式实现更灵活 Rea…...
css实现圆环展示百分比，根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...
k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes（简称K8s）中，Ingress是一个API对象，它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress，你可…...
ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...
什么是EULA和DPA
文章目录 EULA（End User License Agreement）DPA（Data Protection Agreement）一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA（End User License Agreement） 定义： EULA即…...
Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统，支持多语言对话（如 中文，英文，日语），语音情感（如 开心，悲伤）&#x…...
全志A40i android7.1 调试信息打印串口由uart0改为uart3
一，概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本：2014.07； Kernel版本：Linux-3.10； 二，Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01)，并让boo…...
AspectJ 在 Android 中的完整使用指南
一、环境配置（Gradle 7.0 适配） 1. 项目级 build.gradle // 注意：沪江插件已停更，推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...
ip子接口配置及删除
配置永久生效的子接口，2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...
力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...