LeetCode 1237. 找出给定方程的正整数解
原题链接
难度:middle\color{orange}{middle}middle
2023/2/18 每日一题
题目描述
给你一个函数 f(x,y)f(x, y)f(x,y) 和一个目标结果 zzz,函数公式未知,请你计算方程 f(x,y)==zf(x,y) == zf(x,y)==z 所有可能的正整数 数对 xxx 和 yyy。满足条件的结果数对可以按任意顺序返回。
尽管函数的具体式子未知,但它是单调递增函数,也就是说:
- f(x,y)<f(x+1,y)f(x, y) < f(x + 1, y)f(x,y)<f(x+1,y)
- f(x,y)<f(x,y+1)f(x, y) < f(x, y + 1)f(x,y)<f(x,y+1)
函数接口定义如下:
interface CustomFunction {
public:// Returns some positive integer f(x, y) for two positive integers x and y based on a formula.int f(int x, int y);
};
你的解决方案将按如下规则进行评判:
- 判题程序有一个由 CustomFunctionCustomFunctionCustomFunction 的 999 种实现组成的列表,以及一种为特定的 zzz 生成所有有效数对的答案的方法。
- 判题程序接受两个输入:functionidfunction_idfunctionid(决定使用哪种实现测试你的代码)以及目标结果 zzz 。
- 判题程序将会调用你实现的 findSolutionfindSolutionfindSolution 并将你的结果与答案进行比较。
- 如果你的结果与答案相符,那么解决方案将被视作正确答案,即 AcceptedAcceptedAccepted 。
示例 1:
输入:function_id = 1, z = 5
输出:[[1,4],[2,3],[3,2],[4,1]]
解释:function_id = 1 暗含的函数式子为 f(x, y) = x + y
以下 x 和 y 满足 f(x, y) 等于 5:
x=1, y=4 -> f(1, 4) = 1 + 4 = 5
x=2, y=3 -> f(2, 3) = 2 + 3 = 5
x=3, y=2 -> f(3, 2) = 3 + 2 = 5
x=4, y=1 -> f(4, 1) = 4 + 1 = 5
示例 2:
输入:function_id = 2, z = 5
输出:[[1,5],[5,1]]
解释:function_id = 2 暗含的函数式子为 f(x, y) = x * y
以下 x 和 y 满足 f(x, y) 等于 5:
x=1, y=5 -> f(1, 5) = 1 * 5 = 5
x=5, y=1 -> f(5, 1) = 5 * 1 = 5
提示:
- 1<=functionid<=91 <= function_id <= 91<=functionid<=9
- 1<=z<=1001 <= z <= 1001<=z<=100
- 题目保证 f(x,y)==zf(x, y) == zf(x,y)==z 的解处于 1<=x,y<=10001 <= x, y <= 10001<=x,y<=1000 的范围内。
- 在 1<=x,y<=10001 <= x, y <= 10001<=x,y<=1000 的前提下,题目保证 f(x,y)f(x, y)f(x,y) 是一个 32 位有符号整数。
算法
(暴力枚举) O(n2)O(n^2)O(n2)
-
枚举
x和y,调用接口判断f(x, y)是否等于z。 -
如果等于
z,则加入答案中,如果大于z,则终止掉内层循环。
复杂度分析
-
时间复杂度:最坏情况下,需要判断每一个数对,故时间复杂度为 O(n2)O(n^2)O(n2)。
-
空间复杂度 : 需要存储答案,故空间复杂度也为 O(n2)O(n^2)O(n2)。
C++ 代码
/** // This is the custom function interface.* // You should not implement it, or speculate about its implementation* class CustomFunction {* public:* // Returns f(x, y) for any given positive integers x and y.* // Note that f(x, y) is increasing with respect to both x and y.* // i.e. f(x, y) < f(x + 1, y), f(x, y) < f(x, y + 1)* int f(int x, int y);* };*/class Solution {
public:vector<vector<int>> findSolution(CustomFunction& customfunction, int z) {vector<vector<int>> res;for (int x = 1; x <= 1000; x ++) for (int y = 1; y <= 1000; y ++) if (customfunction.f(x, y) == z) {res.push_back({x, y});}return res;}
};
- 双指针
/** // This is the custom function interface.* // You should not implement it, or speculate about its implementation* class CustomFunction {* public:* // Returns f(x, y) for any given positive integers x and y.* // Note that f(x, y) is increasing with respect to both x and y.* // i.e. f(x, y) < f(x + 1, y), f(x, y) < f(x, y + 1)* int f(int x, int y);* };*/class Solution {
public:vector<vector<int>> findSolution(CustomFunction& customfunction, int z) {vector<vector<int>> res;int x = 1, y = 1000;while (x <= 1000 && y >= 1) {int t = customfunction.f(x, y);if (t > z) y --;else if (t < z) x ++;else {res.push_back({x, y});x ++, y --;}}return res;}
};
相关文章:

LeetCode 1237. 找出给定方程的正整数解
原题链接 难度:middle\color{orange}{middle}middle 2023/2/18 每日一题 题目描述 给你一个函数 f(x,y)f(x, y)f(x,y) 和一个目标结果 zzz,函数公式未知,请你计算方程 f(x,y)zf(x,y) zf(x,y)z 所有可能的正整数 数对 xxx 和 yyy。满足条件…...
【ArcGIS Pro二次开发】(5):UI管理_自定义控件的位置
新增的自定义控件一般放在默认的【加载项】选项卡下,但是根据需求,我们可能需要将控件放在新的自定义选项卡下,在自定义选项卡添加系统自带的控件,将自定义的按钮等控件放在右键菜单栏里以方便使用,等等。 下面就以一…...

学习OpenGL图形2D/3D编程
环境:WindowsVisual Studio 2019最流行的几个库:GLUT,SDL,SFML和GLFWGLFWGLAD库查看显卡OPENGL支持情况VS2019glfwgladopenGL3.3顶点着色器片段着色器VAO-VBO-(EBO)->渲染VAO-VBO-EBO->texture纹理矩阵matrix对图形transfor…...

2023美赛思路 | A题时间序列预测任务的模型选择总结
2023美赛思路 | A题时间序列预测任务的模型选择总结 目录 2023美赛思路 | A题时间序列预测任务的模型选择总结基本介绍数据描述任务介绍时序模型基本介绍 这道题分析植被就行,主要涉及不同植被间的相互作用,有竞争有相互促进,我查了下“植物科学数据中心”和“中国迁地保护植…...
PHP教材管理系统设计(源代码+毕业论文)
【P003】PHP教材管理系统设计(源代码论文) 设计方案 本系统采用B/S结构,所有的程序及数据都放在服务器上,终端在取得相应的权限后使用Web页面浏览,录入,修改等功能。在语言方面使用PHP语言,在…...
nps内网穿透工具
一、准备一台有公网ip的服务器 https://github.com/ehang-io/nps/releases 在这个地址下载服务端的安装包,centos的下载这个 上传到服务器上。 二、然后解压,安装,启动 [rootadministrator ~]# tar xzvf linux_amd64_server.tar.gz [roo…...

webpack打包时的热模块替代配置以及source-map
1.HMR 在devServer当中添加hot:true 热模块化功能 含义:当其中有一个文件发生变化的时候,那么就会被重新打包一次,极大的提高了构建速度 A.样式文件:可以使用HMR功能,因为在style-loader当中实现了 B.js文件:默认不能使用HMR功能…...
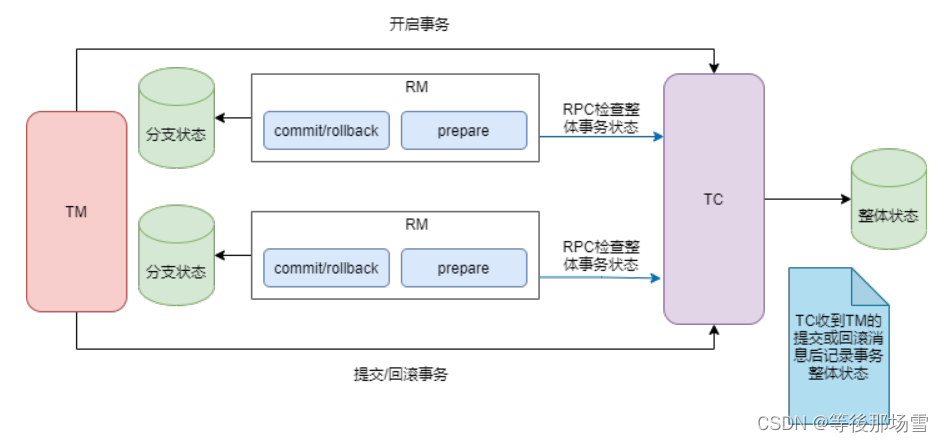
Seata架构篇 - TCC模式
TCC 模式 概述 TCC 是分布式事务中的两阶段提交协议,它的全称为 Try-Confirm-Cancel,即资源预留(Try)、确认操作(Confirm)、取消操作(Cancel)。Try:对业务资源的检查并…...
前端最全面试题整理
前端基础 一、 HTTP/HTML/浏览器 1、说一下 http 和 https https 的 SSL 加密是在传输层实现的。 (1) http 和 https 的基本概念 http: 超文本传输协议,是互联网上应用最为广泛的一种网络协议,是一个客户端和服务器端请求和应答的标准(T…...
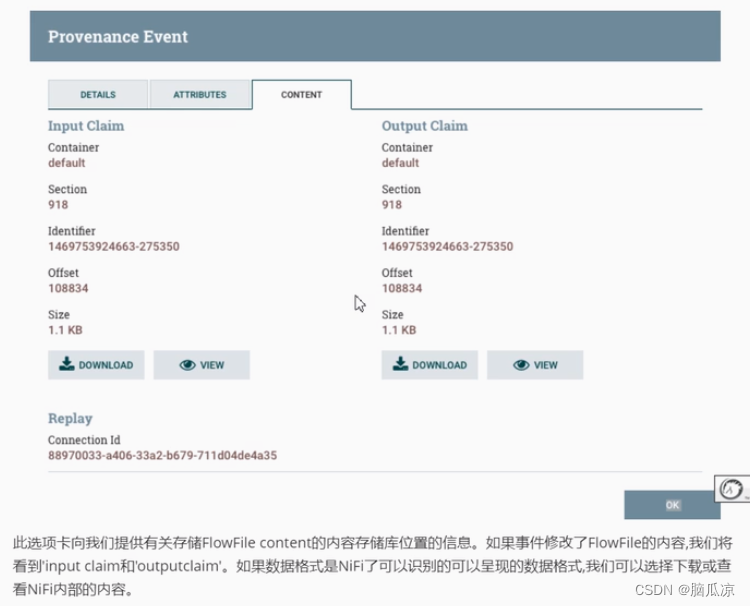
大数据之-Nifi-监控nifi数据流信息_监控数据来源_bub轻松复现---大数据之Nifi工作笔记0011
通过数据流功能可以轻松复现,数据的流向在某个时间点数据是怎么流动的,出现了什么问题,太强大了.. 真的是,可以看到通过右键,处理器,打开view data province就可以看到, 上面是处理器处理数据的详细信息 点击左侧的详情图标可以查看详情信息,details是这个事件处理的内容详情,…...

CUDA编程接口
编程接口 文章目录编程接口3.1利用NVCC编译3.1.1编译流程3.1.1.1 离线编译3.1.1.2 即时编译3.1.2 Binary 兼容性注意:仅桌面支持二进制兼容性。 Tegra 不支持它。 此外,不支持桌面和 Tegra 之间的二进制兼容性。3.1.3 PTX 兼容性3.1.4 应用程序兼容性3.1…...

惠普打印机使用
https://support.hp.com/cn-zh/product/hp-officejet-4500-all-in-one-printer-series-g510/3919445/document/c02076511HP 打印机 - 无法打印校准页本文适用于 HP 喷墨打印机。安装新墨盒后,打印机无法按预期打印校准页。步骤 1:确保打印机可以开始打印…...

Ubuntu升级cmake
目录 1、下载cmake安装包 2、开始安装 3、查看cmake版本 参考链接: https://blog.csdn.net/qq_27350133/article/details/121994229 1、下载cmake安装包 cmake安装包下载:download | cmake 我们根据自身需求下载所需版本的cmake安装包,这…...

CCNP350-401学习笔记(101-150题)
101、Refer to the exhibit SwitchC connects HR and Sales to the Core switch However, business needs require that no traffic from the Finance VLAN traverse this switch. Which command meets this requirement? A. SwitchC(config)#vtp pruning B. SwitchC(config)#…...

分享112个HTML娱乐休闲模板,总有一款适合您
分享112个HTML娱乐休闲模板,总有一款适合您 112个HTML娱乐休闲模板下载链接:https://pan.baidu.com/s/15uBy1SVSckPPMM55fiudeQ?pwdkqfz 提取码:kqfz Python采集代码下载链接:采集代码.zip - 蓝奏云 Bootstrap视频网站模板 …...
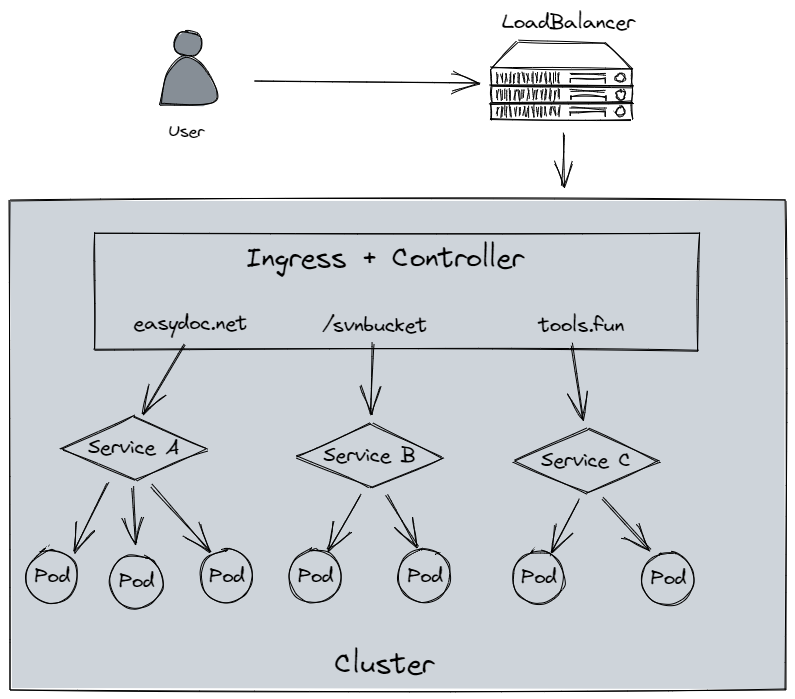
k8s快速入门
文章目录一、Kubernetes(K8S)简介1、概念1.1 Kubernetes (K8S) 是什么1.2 核心特性1.3 部署方案2、Kubernetes 集群架构2.1 架构2.2 重要概念 Pod2.3 Kubernetes 组件二、Kubernetes集群安装1、安装方式介绍2、minikubute安装3、裸机搭建(Bar…...

NG ZORRO知识点总结
NG ZORRO的常用属性,包括但不限于,结合代码 <button nz-button [nzType]"primary" [nzSize]"large" [nzLoading]"loading" [nzDisabled]"disabled" (click)"onClick()">点击我</button>nz-button是一个按钮组件…...

go中的值方法和指针方法
go中的值方法和指针方法1前言2 不同类型的对象调用不同类型的方法2.1 值对象可以调用值方法和指针方法3 指针对象可以调用值方法和指针方法4 !注意:结构体对象实现接口方法1前言 golang中在给结构体对象添加方法时,接收者参数类型可以有两种…...

OKR常见挑战以及应对方法探讨
背景 OKR是大家经常听到的一个词,也有不少团队说自己实行过,但每个实行过的团队都遇到过挑战。很多团队都感觉OKR有些空,很难落地,普通团队成员更是时常感觉无所适从,感觉就像看电影。2022年我们在更大的范围落地了OK…...
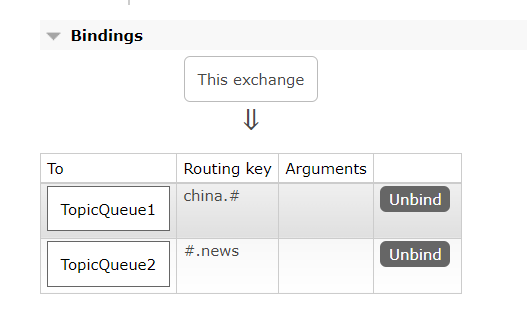
SpringAMQP消息队列(SpringBoot集成RabbitMQ)
一、初始配置1、导入maven坐标<!--rabbitmq--><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-amqp</artifactId></dependency>2、yml配置spring:rabbitmq:host: 你的rabbitmq的ipport: …...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

算法打卡第18天
从中序与后序遍历序列构造二叉树 (力扣106题) 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,7…...
