uniapp软键盘谈起遮住输入框和头部被顶起的问题解决
推荐： pages.json中配置如下可解决头部被顶起和表单被遮住的问题。
{
"path": "pages/debug/protocol/tagWord",
"style": {
"app-plus": {
"softinputMode": "adjustResize"
}
}
},
或
内容区设flex-grow：1，overflow-y:auto; 使其自适应高度并实现滚动；
或
input输入框设置cursor-spacing
相关文章：
uniapp软键盘谈起遮住输入框和头部被顶起的问题解决
推荐： pages.json中配置如下可解决头部被顶起和表单被遮住的问题。 { "path": "pages/debug/protocol/tagWord", "style": { "app-plus": { "soft…...
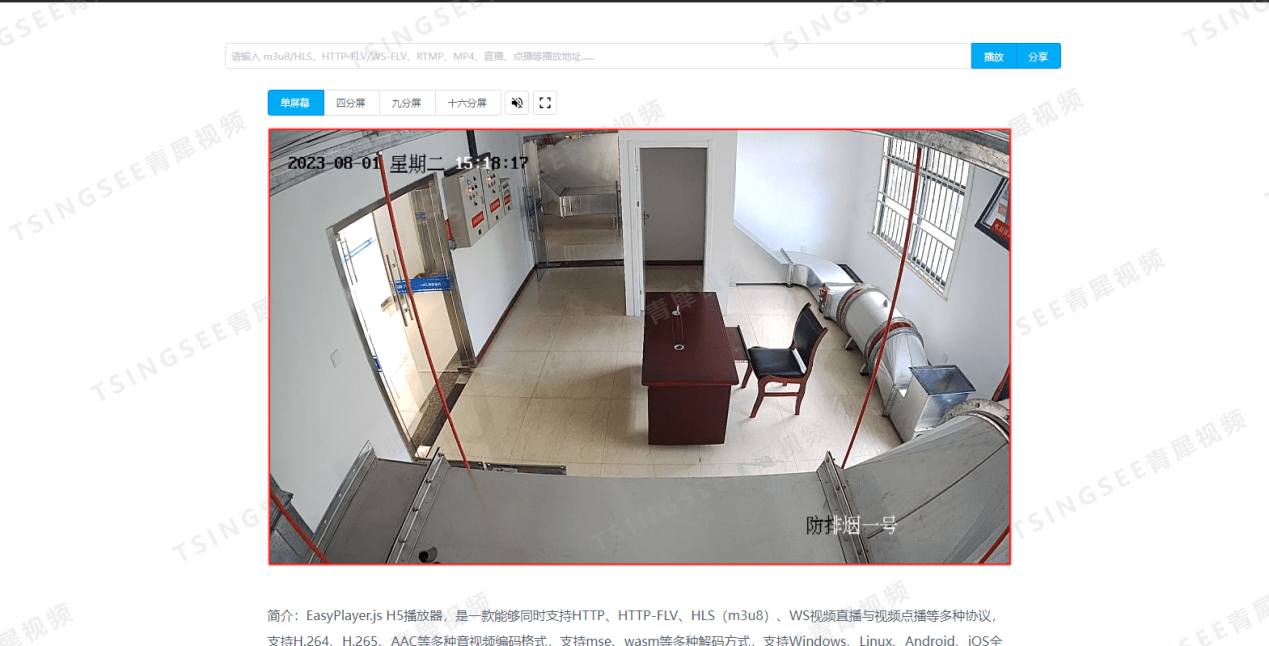
安防监控视频汇聚EasyCVR平台的FLV视频流在VLC中无法播放的原因排查
众所周知，TSINGSEE青犀视频汇聚平台EasyCVR可支持多协议方式接入，包括主流标准协议国标GB28181、RTSP/Onvif、RTMP等，以及厂家私有协议与SDK接入，包括海康Ehome、海大宇等设备的SDK等。在视频流的处理与分发上，视频监控…...
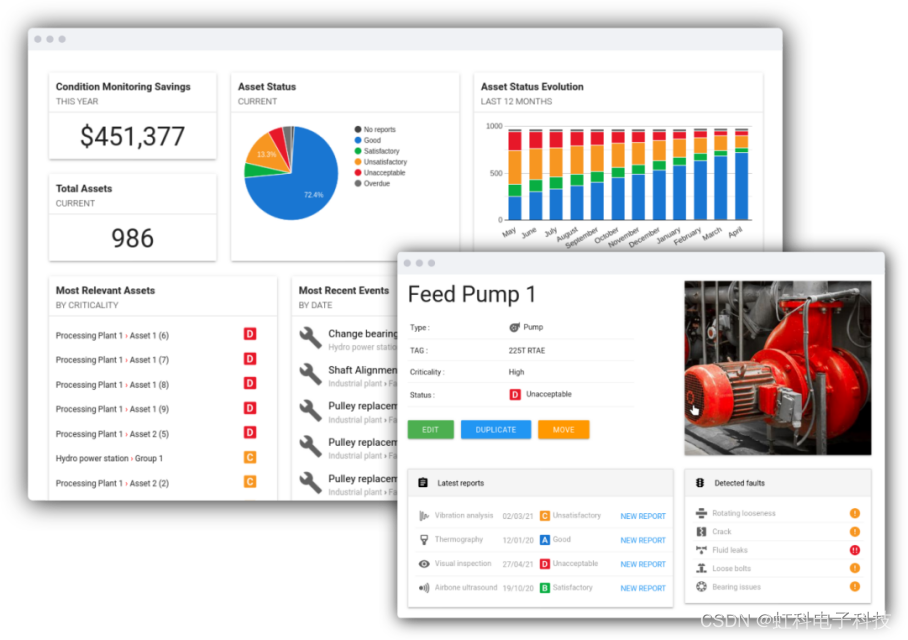
虹科新闻 | 虹科与Power-MI正式建立合作伙伴关系
近日，虹科与Power-MI正式建立合作伙伴关系，双方就工业预测性维护领域进行深入的交流与合作，未来将共同致力于为亚洲市场提供完整的、更高质量的预测性维护解决方案，解决亚洲客户的工业自动化挑战。 虹科与Power-MI都表示十分期待…...
Xamarin.Android实现加载中的效果
目录 1、说明2、代码如下2.1 图1的代码2.1.1、创建一个Activity或者Fragment，如下：2.1.2、创建Layout2.1.3、如何使用 2.2 图2的代码 4、其他补充4.1 C#与Java中的匿名类4.2 、其他知识点 5、参考资料 1、说明 在实际使用过程中，常常会用到点…...
Leetcode.1559 二维网格图中探测环
题目链接 Leetcode.1559 二维网格图中探测环 rating : 1838 题目描述 给你一个二维字符网格数组 g r i d grid grid ，大小为 m x n ，你需要检查 g r i d grid grid 中是否存在 相同值 形成的环。 一个环是一条开始和结束于同一个格子的长度 大于等于…...
阿拉伯数字转中文数字字符，最高支持千京
直接上代码 UtilityClass public class NumberFormatUtil {/** 中文 -> 数字对应关系 */private static final Map<Character, Integer> DIGIT_CHINA new HashMap<>();/** 数字 -> 中文对应关系 */private static final Map<Integer, Character> DIGI…...
Python基础--序列操作/函数
Python基础 1.序列的操作 2.函数 1. 数据类型的具体操作 1.1 序列操作--列表具体操作： #定义列表 listA [] #定义一个空列表 listB [1,2.8,"你好",listA,[1,2,3]] # 访问列表 print(listB)#查看整个列表 print(listB[2])#查看单个…...
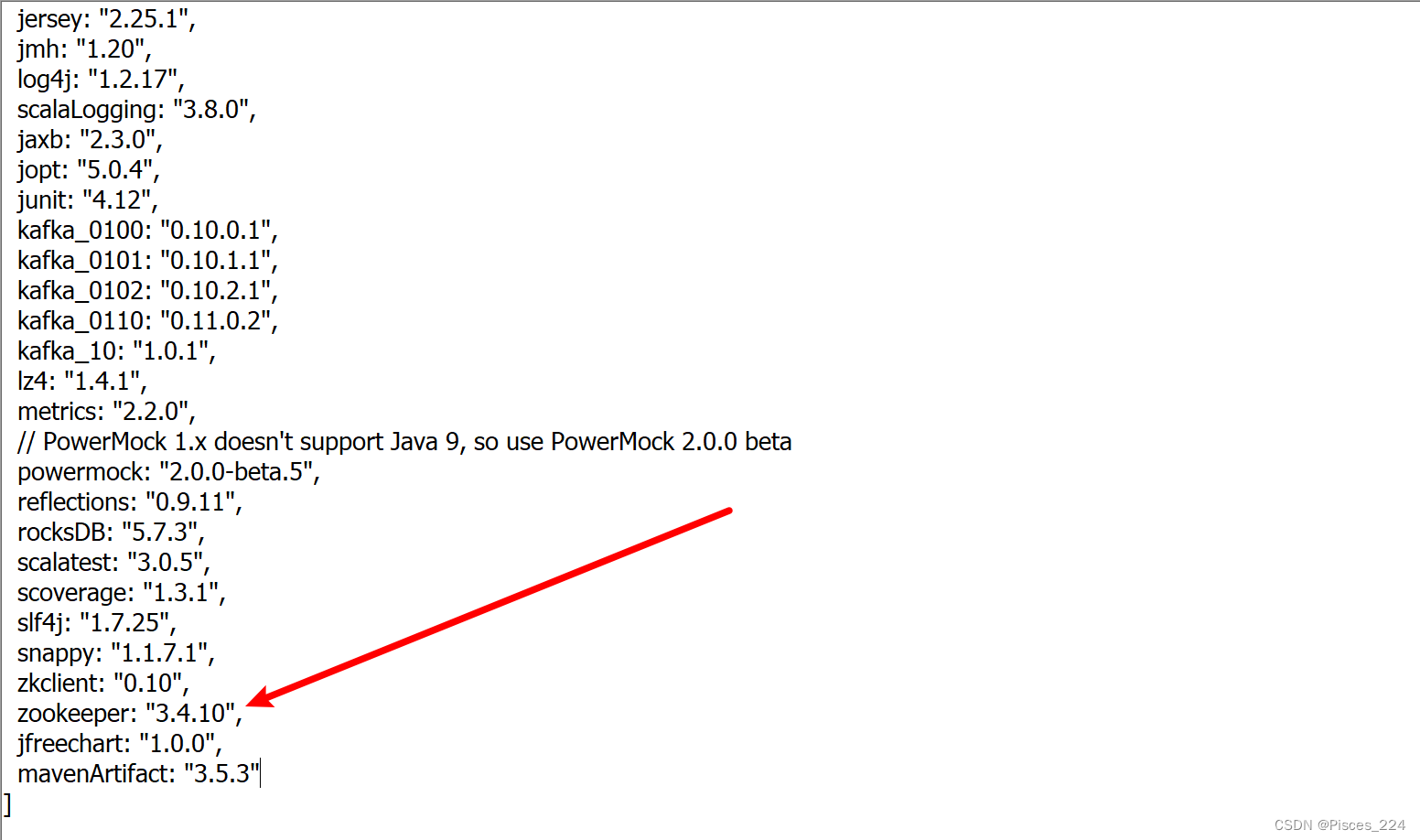
Kafka与Zookeeper版本对应关系
文章目录 了解版本对应Kafka安装包Kafka源码包 了解 比如： kafka_2.11-1.1.1.jar包 其中2.11表示的是Scala的版本，因为Kafka服务器端代码完全由Scala语音编写。”-“后面的1.1.1表示的kafka的版本信息。遵循一个基本原则，Kafka客户端版本和服…...
Arch Linux 使用桥接模式上网
如果我们想要将虚拟机与物理主机同一网段，并且像物理机器一样被其他设备访问，则需要以桥接模式上网，这个时候，物理主机就必须配置为使用网桥上网了。 注意：这里我们使用了 NetworkManager 网络管理工具中的 nmcli 来进…...
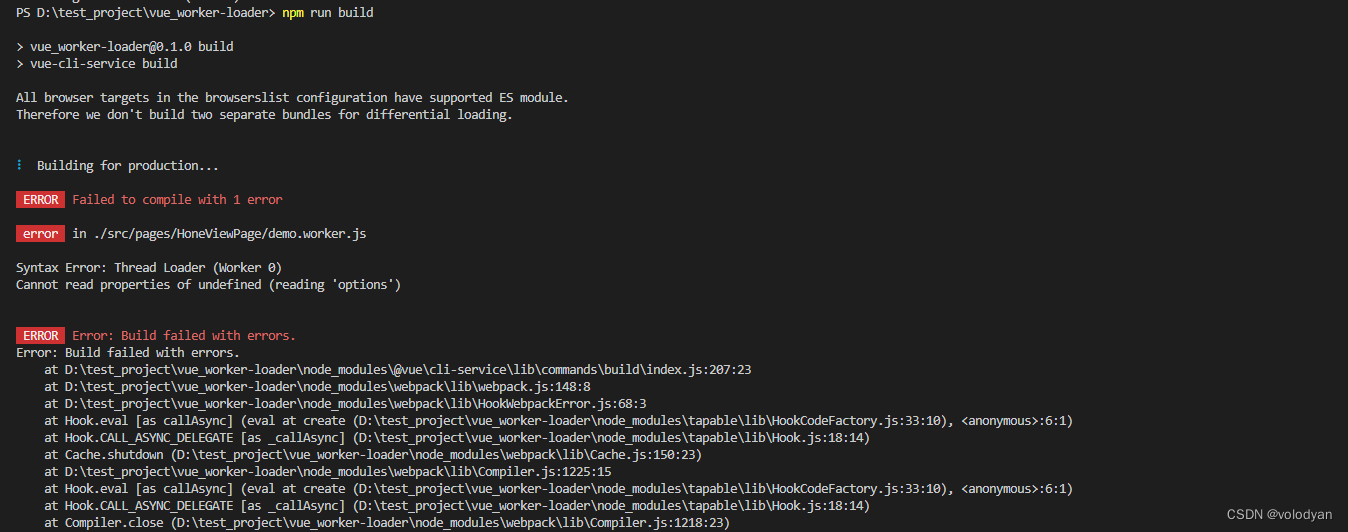
Vue 中使用 WebWorker
目录 安装 loader 应用场景 打包时错误处理 安装 loader npm install worker-loader -D 如果直接把worker.js放到public目录下，则不需要安装loader vue.config.js const { defineConfig } require(vue/cli-service)module.exports defineConfig({transpileDe…...
财务管理系统javaweb会计账房进销存jsp源代码mysql
本项目为前几天收费帮学妹做的一个项目，Java EE JSP项目，在工作环境中基本使用不到，但是很多学校把这个当作编程入门的项目来做，故分享出本项目供初学者参考。 一、项目描述 财务管理系统javaweb java,Struts2,bootstrap,mysql,…...
企业服务器被devos勒索病毒攻击后怎么处理，devos勒索病毒如何攻击的
众所周知，科学技术是第一生产力，科学技术的发展给企业与人们的生活带来了极大变化，但随之而来的网络安全威胁也不断增加。最近，我们收到很多企业的求助，企业的计算机服务器遭到了devos勒索病毒的攻击，导致企…...
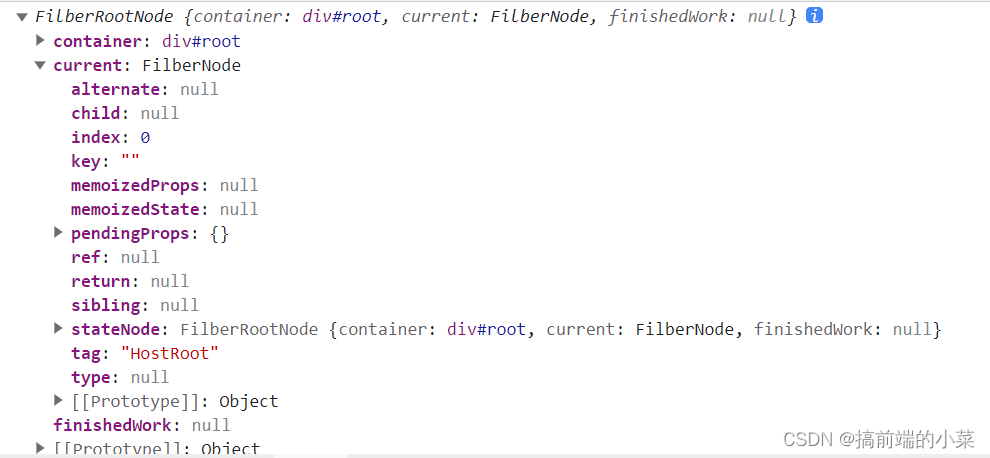
React源码解析18（2）------ FilberNode，FilberRootNode结构关系
摘要 在上一篇，我们实现了通过JSX转换为ReactElement的方法，也看到了转换后React元素的结构。但是这个React元素，并不能很清楚的表达组件之间的关系，以及属性的处理。 所以在React内部，会将所有的React元素转换为Fil…...
什么是Session？它在SQLAlchemy中扮演什么角色？
让我们先来谈谈什么是“Session”。在你逛超市或者餐厅的时候，你可能会遇到一种叫做“前台”的东西。你知道那是干什么的吗？它是用来暂存你买的东西，这样你就可以从容地结账，而不必抱着满满一购物车的商品。 数据库的“Session”…...
Java 中 Set集合常用方法
.add() 添加元素 对象名.add() 向Set集合中添加元素 （但不能添加重复元素，Set集合中不允许元素重复） Set<String> s new HashSet<String>(); // 添加数据 s.add("aaa"); s.add("bbb"); addAll(Collectio…...
（MVC）SpringBoot+Mybatis+Mapper.xml
前言：本篇博客主要对MVC架构、Mybatis工程加深下理解，前面写过一篇博客：SprintBoothtml/css/jsmybatis的demo，里面涉及到了Mybatis的应用，此篇博客主要介绍一种将sql语句写到了配置文件里的方法，即Mybatis里…...
【Linux命令行与Shell脚本编程】第十九章 正则表达式
Linux命令行与Shell脚本编程 第十九章 正则表达式 文章目录 Linux命令行与Shell脚本编程 第十九章 正则表达式九.正则表达式9.1.正则表达式基础9.1.1.正则表达式的类型9.2.定义BRE模式9.2.1.普通文本9.2.2.特殊字符 9.2.3.锚点字符锚定行首^锚定行尾$组合锚点 9.2.4.点号字符\.…...
vue exceljs 实现导出excel并设置网格线、背景色、 垂直居中、分页打印
一、 下载 exceljs pnpm install exceljs二、 页面中使用 // 导出 exportExcelexportToExcel() {this.$confirm("此操作将导出excel文件, 是否继续?", "提示", {confirmButtonText: "确定",cancelButtonText: "取消",type: "wa…...
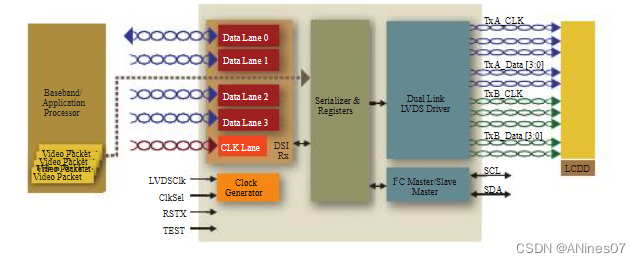
TC358774/5显示桥接(MIPI DSI到LVDS)
东芝TC358774/5显示桥针对使用带有MIPI DSI(显示串行接口)连接的主机处理器的手持设备进行了优化。tc358774 /5作为协议桥接，使视频数据流从主机处理器链接到驱动LVDS显示面板。tc358774 /5桥接器可以配置为多达4通道MIPI DSI，每通道数据速率高达1 Gbps&…...
企业内部FAQ常见问题展示分享的价值
企业内部FAQ（常见问题）展示分享是一种将常见问题和解决方案以问答形式呈现给员工的方式。这种方式可以帮助企业提高工作效率、提供一致的解决方案、提升员工满意度和减少重复工作。 企业内部FAQ常见问题展示分享的价值： 1. 提高工作效率 企…...
【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板，载入页面后，会显示引导弹窗，适用于引导用户使用页面，点击完成后，会显示下一个引导弹窗，直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...
srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935，SRS管理页面端口是8080，可…...
C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...
鱼香ros docker配置镜像报错：https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题：docker pull 失败 网络不同，需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...
基于Java Swing的电子通讯录设计与实现：附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用，结合SQLite数据库实现联系人管理功能，并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能，同时可以最小化到系统…...
Spring是如何解决Bean的循环依赖：三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中，Bean 的循环依赖是指多个 Bean 之间互相持有对方引用，形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路，例如： 双向依赖：Bean A 依赖 Bean B，同时 Bean B 也依赖 Bean A（A↔B）。链条循环： Bean A → Bean…...
如何更改默认 Crontab 编辑器 ？
在 Linux 领域中，crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用，用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益，允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...
LRU 缓存机制详解与实现（Java版） + 力扣解决
📌 LRU 缓存机制详解与实现（Java版） 一、📖 问题背景 在日常开发中，我们经常会使用 缓存（Cache） 来提升性能。但由于内存有限，缓存不可能无限增长，于是需要策略决定&am…...
热烈祝贺埃文科技正式加入可信数据空间发展联盟
2025年4月29日，在福州举办的第八届数字中国建设峰会“可信数据空间分论坛”上，可信数据空间发展联盟正式宣告成立。国家数据局党组书记、局长刘烈宏出席并致辞，强调该联盟是推进全国一体化数据市场建设的关键抓手。 郑州埃文科技有限公司&am…...
PH热榜 | 2025-06-08
1. Thiings 标语：一套超过1900个免费AI生成的3D图标集合 介绍：Thiings是一个不断扩展的免费AI生成3D图标库，目前已有超过1900个图标。你可以按照主题浏览，生成自己的图标，或者下载整个图标集。所有图标都可以在个人或…...