【数学建模】-- Matlab中图的最短路径
前言:
图的基本概念:
若想简单绘制图可以利用此网站: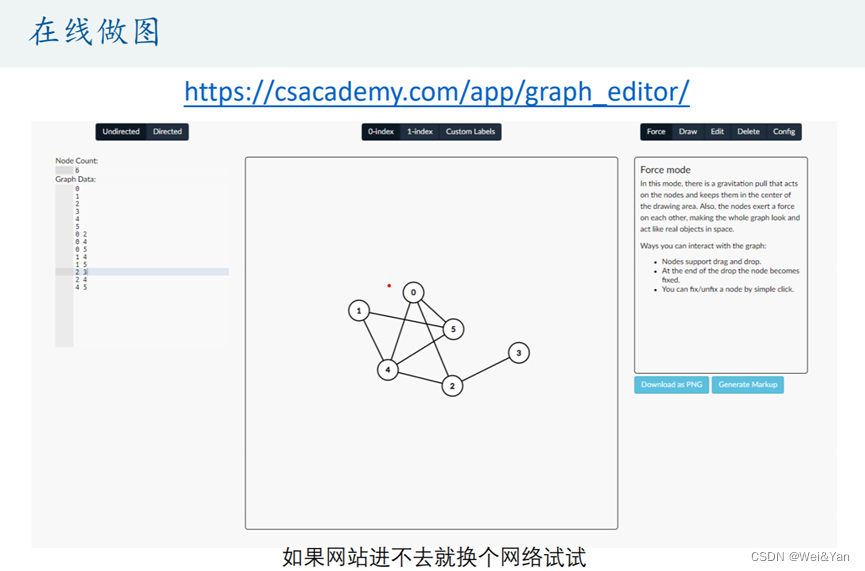
左上角Undirected/Directed是无向图/有向图
左边 0-index ,1-index为0下标,1下标。
Node Count为节点个数
Graph Data:最初尾节点的名称(一个数据)
相连两节点的名称与两节点连线的权重(三个数据)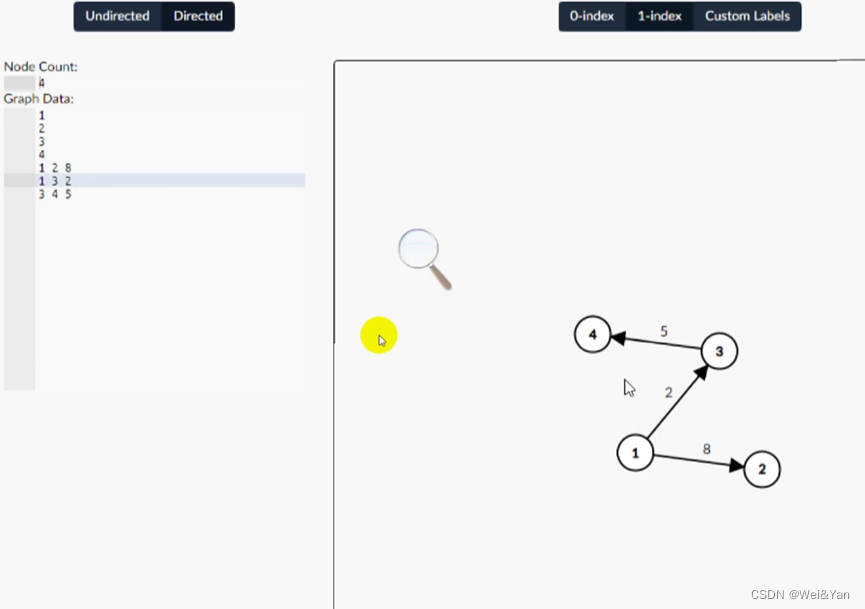
利用matlab制作 “图”:
Graph中的s,t指的图中顶点的名称,而且元素数量必须相同,s和t对应位置的数据会在构中相连。
注意事项:
- 在结点名称中若我们使用的是字符串,需要用大括号{},中间的字符名称需要用 ‘’引起。

2.若结点名为常数,这些结点必须都是从1开始的正整数。
Graph中的第三个元素为权重,权重对应的则是节点之间相连的线。
Matlab中的有向图:
函数为:digraph()
无向图的权重邻接矩阵: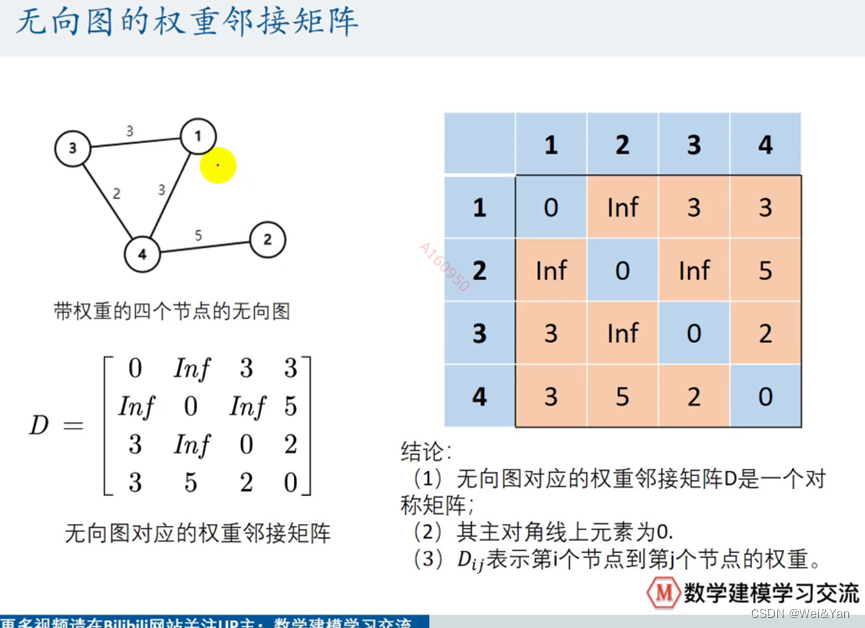
有向图的权重邻接矩阵:
求最小路径的算法:迪杰斯特拉算法:
博主之前在学习数据结构的时候创作过一篇关于迪杰斯特拉的文章:数据结构 -最短路径dijkstra(迪杰斯特拉)算法讲解及代码实现_地杰斯特拉_Wei&Yan的博客-CSDN博客可以参考里面的内容。
迪杰斯特拉的缺点:
如何修复该缺点:
什么是负权回路?
(注意无向图中的一条负权边也属于负权回路,如下图中结点3与结点2之间权重为-2的回路。)

在matlab中有计算最短路径的函数:
Shortserpath(图名称,起始节点,终点结点)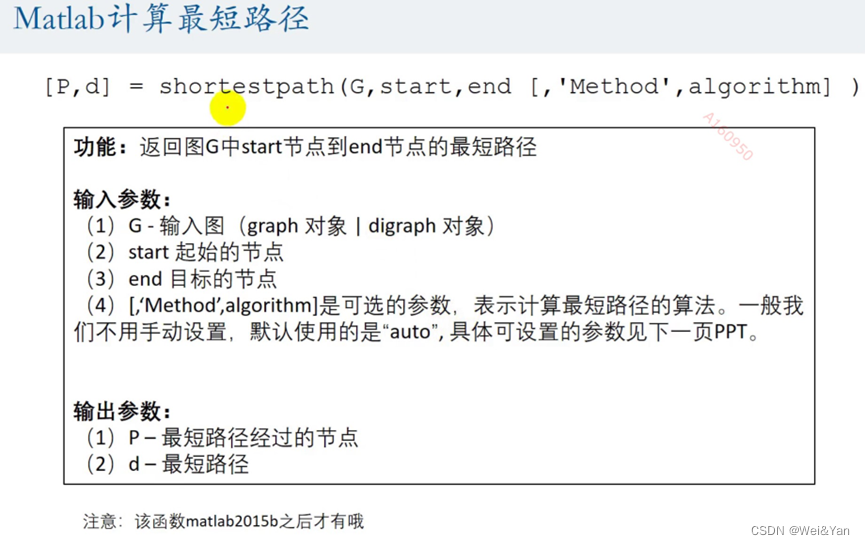
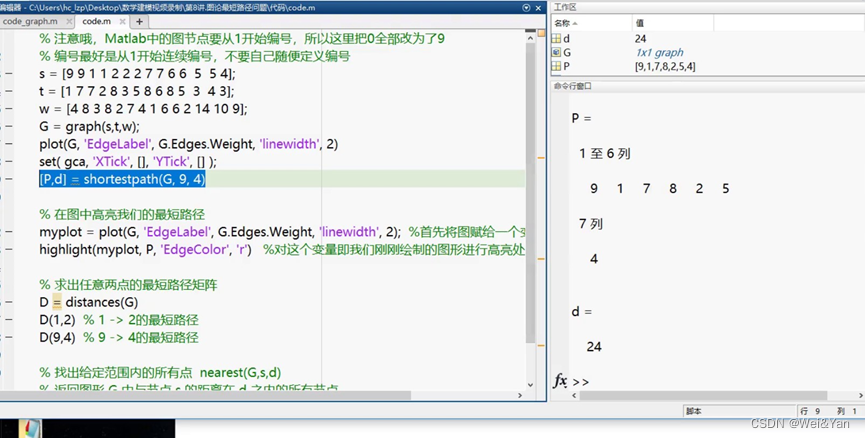
在图中高亮出图的最短路径
Highlight(plot的变量名,shortestpath中接受的P,‘EdgeColor’,‘颜色’)
返回任意两点的距离矩阵
找给定范围内所有的点: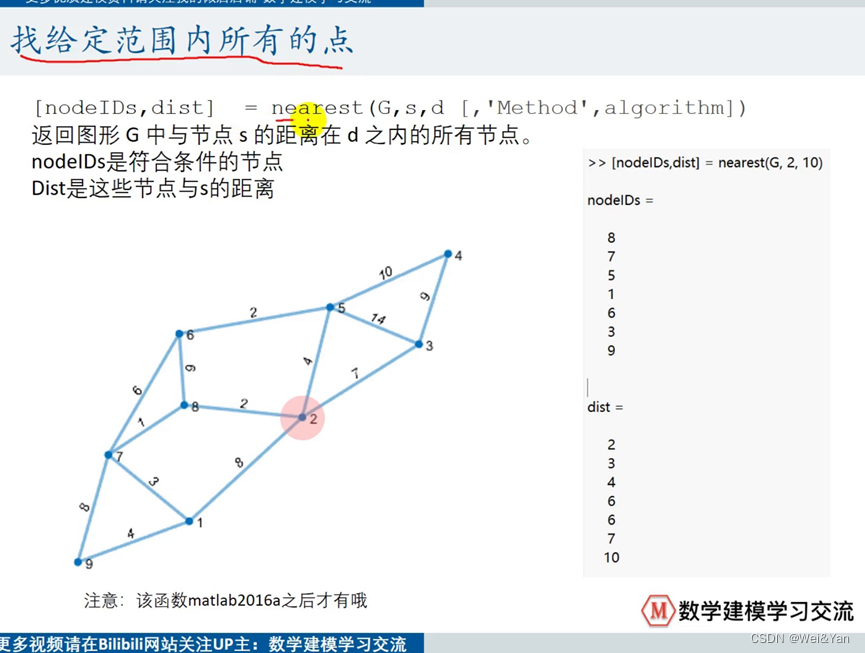
课后作业:
只需要找出最短路径和长度即可。(最好可以将最短路径) 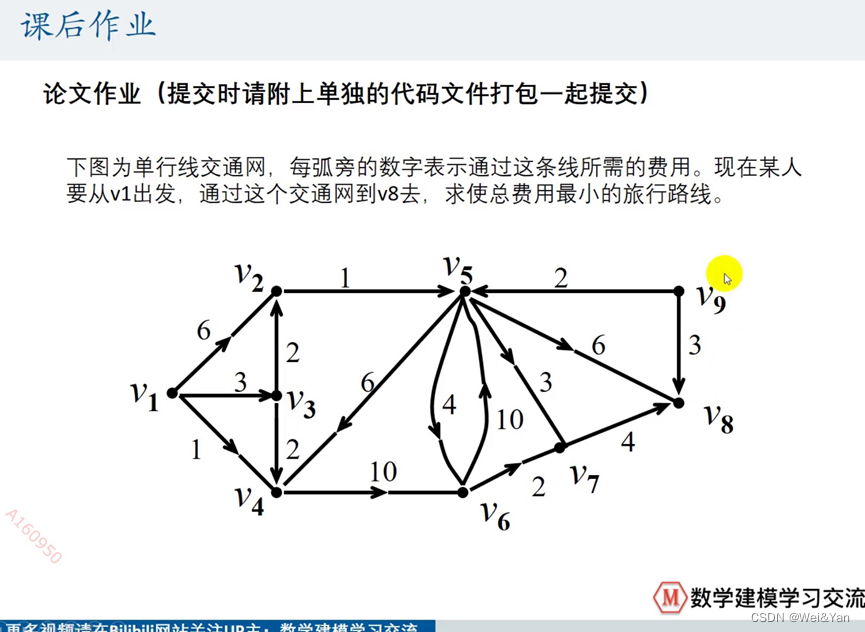
参考代码:
%创建图的顶点和边
s = {'v1','v1','v1','v2','v3','v3','v4','v5','v5','v5','v5','v6','v6','v7','v9','v9'};
t = {'v4','v2','v3','v5','v4','v2','v6','v4','v6','v7','v8','v5','v7','v8','v5','v8'};
w = [1,6,3,1,2,2,10,6,4,3,6,10,2,4,2,3];
G = digraph(s,t,w);
myplot = plot(G,'EdgeLabel',G.Edges.Weight,'LineWidth',2);%求出最短路径
[P,d] = shortestpath (G,'v1','v8')
highlight (myplot,P,'EdgeColor','red')博主曾经也写过一篇关于数据结构图的博客 :图的基本概念和术语_Wei&Yan的博客-CSDN博客
相关文章:

【数学建模】-- Matlab中图的最短路径
前言: 图的基本概念: 若想简单绘制图可以利用此网站: 左上角Undirected/Directed是无向图/有向图 左边 0-index ,1-index为0下标,1下标。 Node Count为节点个数 Graph Data:最初尾节点的名称ÿ…...

中国月入过万的人多不多
Q:中国月入过万的人多不多 单从这个问题来看,这是个费米问题啊: 估算中国月入过万的有多少人? 要解决费米问题,其实也很好办,就是逻辑拆解,这篇文章也分为3个部分,先从公开数据中估…...

苹果电脑图像元数据编辑器:MetaImage for Mac
MetaImage for Mac是一款功能强大的照片元数据编辑器,它可以帮助用户编辑并管理照片的元数据信息,包括基本信息和扩展信息。用户可以根据需要进行批量处理,方便快捷地管理大量照片。 MetaImage for Mac还提供了多种导入和导出格式࿰…...
 详解)
BeanUtils.copyProperties() 详解
BeanUtils.copyProperties会进行类型转换; BeanUtils.copyProperties方法简单来说就是将两个字段相同的对象进行属性值的复制。如果 两个对象之间存在名称不相同的属性,则 BeanUtils 不对这些属性进行处理,需要程序手动处理。 这两个类在不同…...

基于CentOS 7构建LVS-DR集群
DIPVIPRIPClient192.169.41.139 LVS 192.168.41.134192.169.41.10RS1192.168.41.135RS2192.168.41.138 要求: node4为客户端,node2为LVS,node3和node4为RS。 1.配置DNS解析(我这里使用本地解析) 192.168.41.134 www.y…...

openEuler-OECA考试报名火热开启,尊享半价优惠 作者:HopeInfra 发布时间:2023-08-10
近日,润和软件人才评定报名系统已成功上线运行,现openEuler-OECA人才评定考试报名优惠活动火热开启,欢迎大家报名咨询! 关于openEuler人才评定 随着openEuler及其发行版本在各个行业使用量逐年增多,相关人才的评定诉求…...
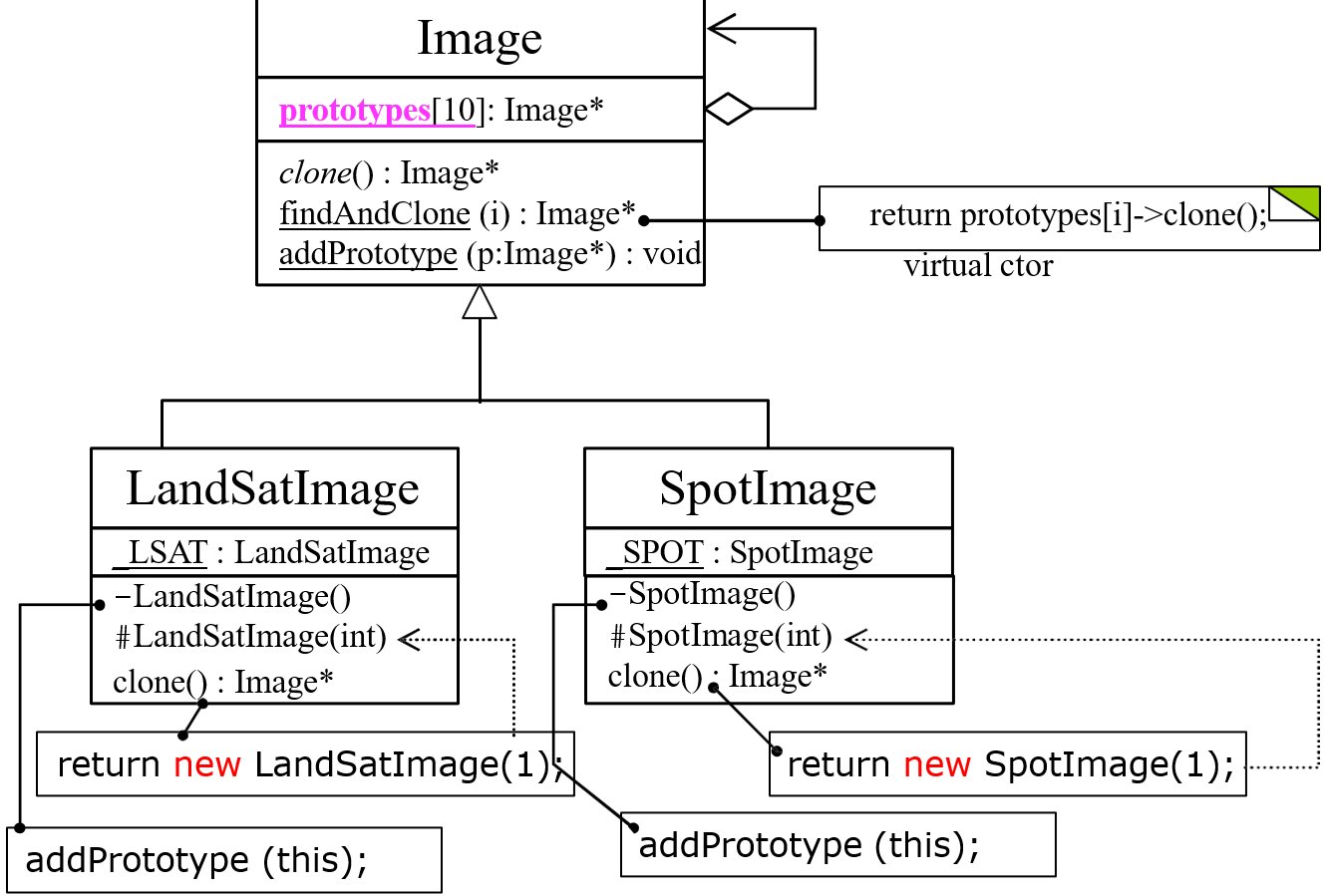
侯捷 C++面向对象编程笔记——10 继承与虚函数
10 继承与虚函数 10.1 Inheritance 继承 语法::public base_class_name public 只是一种继承的方式,还有protect,private 子类会拥有自己的以及父类的数据 10.1.1 继承下的构造和析构 与复合下的构造和析构相似 构造是由内而外 Container …...
、计算日期之间的天数等))
mysql日期函数(查询最近n(天/月/年)、计算日期之间的天数等)
mysql日期函数 目录 mysql查询最近一个月数据返回当前日期和时间将字符串转变为日期日期 d 减去 n 天后的日期计时间差,返回 datetime_expr2 − datetime_expr1 的时间差算查询当天数据 ADDDATE(d,n)计算起始日期 d 加上 n 天的日期 SELECT ADDDATE("2017-06…...

通过anvt X6和vue3实现图编辑
通过anvt X6 X6地址:https://x6.antv.antgroup.com/tutorial/about; 由于节点比较复杂,使用vue实现的节点; x6提供了一个独立的包 antv/x6-vue-shape 来使用 Vue 组件渲染节点。 VUE3的案例: <template><div…...

win2012 IIS8.5 安装PHP教程,一些版本不能用
因为一直用win2003IIS6.0PHP的环境,所以搭建PHP自认为非常熟悉了,但是最近在搭建win2012IIS8.5PHP的环境时,我遇到了一些问题,经过4个小时的折腾,终于搞定了,本文记录一些经验,可能不少朋友也会…...

sqlalchemy执行原生sql
# 有的复杂sql 用orm写不出来---》用原生sql查询 # 原生sql查询,查出的结果是对象 # 原生sql查询,查询结果列表套元组 准备工作 from sqlalchemy.orm import sessionmaker, relationship from sqlalchemy import create_engineengine create_engine(&…...

Python-OpenCV中的图像处理-图像平滑
Python-OpenCV中的图像处理-图像平滑 图像平滑平均滤波高斯模糊中值模糊双边滤波 图像平滑 使用低通滤波器可以达到图像模糊的目的。这对与去除噪音很有帮助。其实就是去除图像中的高频成分(比如:噪音,边界)。所以边界也会被模糊…...
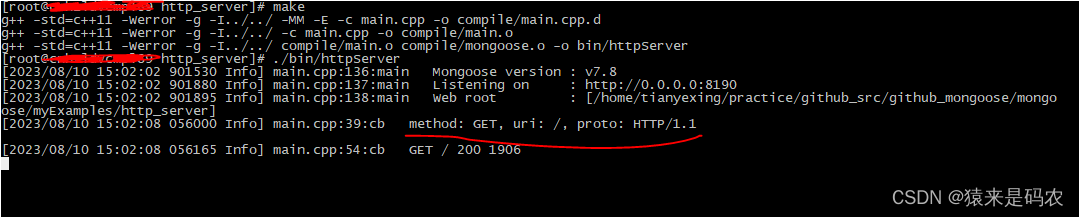
Mongoose http server 例子
今天抽了点时间看了一下 mongoose的源码, github 地址,发现跟以前公司内部使用的不太一样,这里正好利用其 http server 例子来看一下。以前的 http message 结构体是这样的: /* HTTP message */ struct http_message {struct mg_…...

1、初识HTML
1、初识HTML 前端就是写一些基本的页面,HTML即超文本标记语言:Hyper Text Markup Language,超文本包括,文字、图片、音频、视频、动画等,HTML5,提供了一些新的元素和一些有趣的新特性,同时也建…...

线性代数(三) 线性方程组
前言 如何利用行列式,矩阵求解线性方程组。 线性方程组的相关概念 用矩阵方程表示 齐次线性方程组:Ax0;非齐次线性方程组:Axb. 可以理解 齐次线性方程组 是特殊的 非齐次线性方程组 如何判断线性方程组的解 其中R(A)表示矩阵A的…...

Apoll 多项式规划求解
一、纵向规划 void QuarticPolynomialCurve1d::ComputeCoefficients(const float x0, const float dx0, const float ddx0, const float dx1,const float ddx1, const float p) {if (p < 0.0) {std::cout << "p should be greater than 0 at line 140." &…...
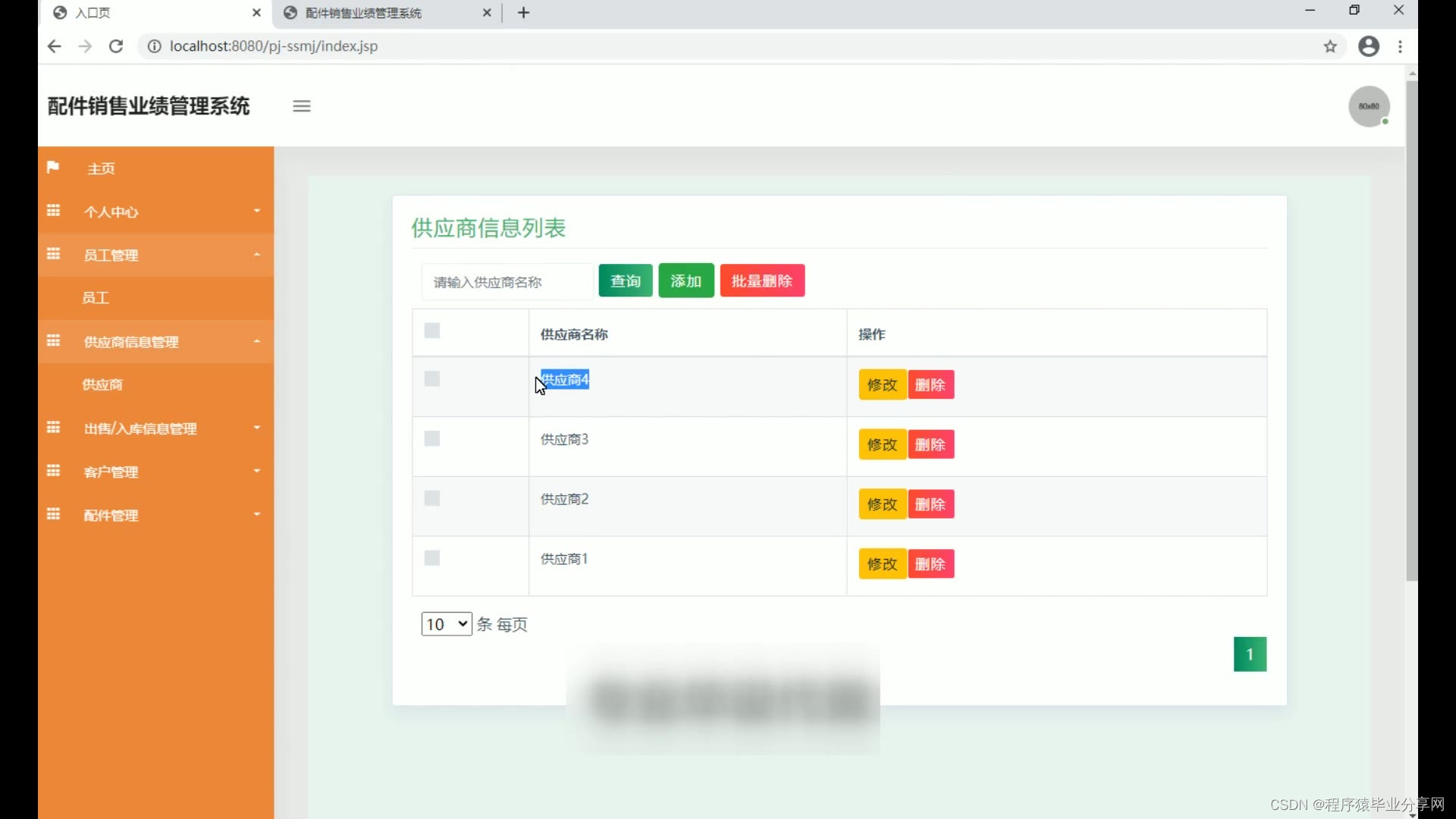
ssm亚盛汽车配件销售业绩管理统源码和论文PPT
ssm亚盛汽车配件销售业绩管理统源码和论文PPT007 开发工具:idea 数据库mysql5.7(mysql5.7最佳) 数据库链接工具:navcat,小海豚等 开发技术:java ssm tomcat8.5 研究的意义 汽车配件销售类企业近年来得到长足发展,在市场份额不断扩大同时…...
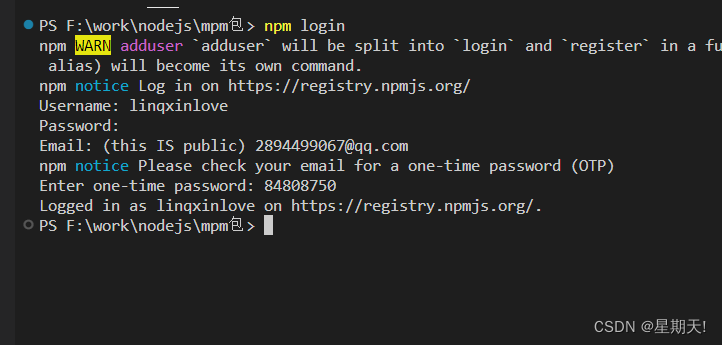
发布属于自己的 npm 包
1 创建文件夹,并创建 index.js 在文件中声明函数,使用module.exports 导出 2 npm 初始化工具包,package.json 填写包的信息(包的名字是唯一的) npm init 可在这里写包的名字,或者一路按回车,后…...

Redis主从复制和哨兵架构图,集成Spring Boot项目实战分享
目录 1. Redis 主从复制2. Redis 哨兵架构3. 集成spring boot项目案列 Redis 主从复制和哨兵架构是 Redis 集群的重要组成部分,用于提高 Redis 集群的可用性和性能。以下是 Redis 主从复制和哨兵架构的详细介绍,包括架构图和 Java 代码详解。 1. Redis …...
java中try-with-resources自动关闭io流
文章目录 java中try-with-resources自动关闭io流0 简要说明try-with-resources java中try-with-resources自动关闭io流 0 简要说明 在传统的输入输出流处理中,我们一般使用的结构如下所示,使用try - catch - finally结构捕获相关异常,最后不…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...
