线性代数(三) 线性方程组
前言
如何利用行列式,矩阵求解线性方程组。
线性方程组的相关概念

用矩阵方程表示
- 齐次线性方程组:Ax=0;
- 非齐次线性方程组:Ax=b.
可以理解 齐次线性方程组 是特殊的 非齐次线性方程组
如何判断线性方程组的解

- 其中R(A)表示矩阵A的秩
- B表示A的增广矩阵
- n表示末知数个数

增广矩阵

矩阵的秩



秩r<= 未知数的数量n
r=n时,称为满秩
如何求解矩阵A的秩
- 矩阵经过初等变化后秩不变
- r+1阶子式的行列式=0的特性
可以将矩阵转为化

矩阵的秩,就是矩阵初等变换后化成行阶梯形时的非零行的行数。

- 方程组的系数矩阵的秩与方程组增广矩阵的秩相等。方程组里的所有方程都是不冲突的,不会出现等式左边都是“x+y”,右边却一个是“1”,一个是“3”的情况,因为这样会得出1=3的错误等式,令方程组无解。
- 方程组的系数矩阵的秩等于未知数的个数。方程组里的方程,必须有n个是不能相互推出,这个n,便是未知数的个数。像前文举例的“x+y=2”和“2x+2y=4”,便只能属于是一个方程,因为后者可以通过前者乘以2得出。
- 当方程组的系数矩阵的秩与方程组增广矩阵的秩相等且均小于方程组中未知数个数n的时候,方程组有无穷多解。当所有的方程都不冲突,但存在一个或一个以上的方程是可以由其他方程变换过来的,这就相当于n个未知数,却没有n个方程,自然就是无穷多解了。
- 当方程组的系数矩阵的秩小于方程组增广矩阵的秩的时候,方程组无解。存在两个或多个方程有冲突,那别说了,直接无解就是了
增广矩阵求解

其计算过程还是通过消元法来解方程组。
克拉默法则
当矩阵A的行列式det(A)!=0时,可使用行列式的解方程- 克拉默法则求解
求多解

可见上述方程组的解,是一个集合,怎么表示这个集合?

基础解系
指在无穷多组解中,找到一组解,且满足:
- 这组解内的向量线性无关
- 方程组的任意一个解都可由这组向量线性表示
那么这组解(向量组),就称为基础解系
实际上这和极大线性无关组是一回事
再将上述基础解系a,带入齐次线性方程组 A x ⃗ = 0 ⃗ A\vec{x}=\vec{0} Ax=0
通解为
x ⃗ = k 1 ∗ a ⃗ \vec{x}=k_1*\vec{a} x=k1∗a
其中: k 1 k_1 k1取任意常数
通解就是线性方程组解的具体表达方式
向量组



如果R(A)=m,则表示有解。即得不出上述 y = − z y=-z y=−z y和z变量的相关性

主要参考
《如何理解矩阵的「秩」?》
《线性方程组在什么时候有唯一解/无穷个解/无解?》
《11.2 齐次线性方程组的基础解系和通解》
相关文章:

线性代数(三) 线性方程组
前言 如何利用行列式,矩阵求解线性方程组。 线性方程组的相关概念 用矩阵方程表示 齐次线性方程组:Ax0;非齐次线性方程组:Axb. 可以理解 齐次线性方程组 是特殊的 非齐次线性方程组 如何判断线性方程组的解 其中R(A)表示矩阵A的…...

Apoll 多项式规划求解
一、纵向规划 void QuarticPolynomialCurve1d::ComputeCoefficients(const float x0, const float dx0, const float ddx0, const float dx1,const float ddx1, const float p) {if (p < 0.0) {std::cout << "p should be greater than 0 at line 140." &…...
ssm亚盛汽车配件销售业绩管理统源码和论文PPT
ssm亚盛汽车配件销售业绩管理统源码和论文PPT007 开发工具:idea 数据库mysql5.7(mysql5.7最佳) 数据库链接工具:navcat,小海豚等 开发技术:java ssm tomcat8.5 研究的意义 汽车配件销售类企业近年来得到长足发展,在市场份额不断扩大同时…...
发布属于自己的 npm 包
1 创建文件夹,并创建 index.js 在文件中声明函数,使用module.exports 导出 2 npm 初始化工具包,package.json 填写包的信息(包的名字是唯一的) npm init 可在这里写包的名字,或者一路按回车,后…...

Redis主从复制和哨兵架构图,集成Spring Boot项目实战分享
目录 1. Redis 主从复制2. Redis 哨兵架构3. 集成spring boot项目案列 Redis 主从复制和哨兵架构是 Redis 集群的重要组成部分,用于提高 Redis 集群的可用性和性能。以下是 Redis 主从复制和哨兵架构的详细介绍,包括架构图和 Java 代码详解。 1. Redis …...
java中try-with-resources自动关闭io流
文章目录 java中try-with-resources自动关闭io流0 简要说明try-with-resources java中try-with-resources自动关闭io流 0 简要说明 在传统的输入输出流处理中,我们一般使用的结构如下所示,使用try - catch - finally结构捕获相关异常,最后不…...

Games101学习笔记 -光栅化
光栅化 经过MVP矩阵和视口变换后,我们就可以从相机的角度看到一个和屏幕大小一致的二维平面。 那么把这个看到的二维平面应用到我们的屏幕上的过程就是光栅化。在这儿我们需要补充一个概念-像素: 像素: 一个二位数组,数组中每个…...

Pytorch量化之Post Train Static Quantization(训练后静态量化)
使用Pytorch训练出的模型权重为fp32,部署时,为了加快速度,一般会将模型量化至int8。与fp32相比,int8模型的大小为原来的1/4, 速度为2~4倍。 Pytorch支持三种量化方式: 动态量化(Dynamic Quantization&…...

Sql奇技淫巧之EXIST实现分层过滤
在这样一个场景,我 left join 了很多张表,用这些表的不同列来过滤,看起来非常合理 但是出现的问题是 left join 其中一张或多张表出现了笛卡尔积,且无法消除 FUNCTION fun_get_xxx_helper(v_param_1 VARCHAR2,v_param_2 VARCHAR2…...

Linux下升级jdk1.8小版本
先输入java -version 查看是否安装了jdk java -version (1)如果没有返回值,直接安装新的jdk即可。 (2)如果有返回值,例如: java version "1.8.0_251" Java(TM) SE Runtime Enviro…...

【Mysql】数据库基础与基本操作
🌇个人主页:平凡的小苏 📚学习格言:命运给你一个低的起点,是想看你精彩的翻盘,而不是让你自甘堕落,脚下的路虽然难走,但我还能走,比起向阳而生,我更想尝试逆风…...

87 | Python人工智能篇 —— 机器学习算法 决策树
本教程将深入探讨决策树的基本原理,包括特征选择方法、树的构建过程以及剪枝技术,旨在帮助读者全面理解决策树算法的工作机制。同时,我们将使用 Python 和 scikit-learn 库演示如何轻松地实现和应用决策树,以及如何对结果进行可视化。无论您是初学者还是有一定机器学习经验…...
【计算机视觉】干货分享:Segmentation model PyTorch(快速搭建图像分割网络)
一、前言 如何快速搭建图像分割网络? 要手写把backbone ,手写decoder 吗? 介绍一个分割神器,分分钟搭建一个分割网络。 仓库的地址: https://github.com/qubvel/segmentation_models.pytorch该库的主要特点是&#…...
解析湖仓一体的支撑技术及实践路径
自2021年“湖仓一体”首次写入Gartner数据管理领域成熟度模型报告以来,随着企业数字化转型的不断深入,“湖仓一体”作为新型的技术受到了前所未有的关注,越来越多的企业视“湖仓一体” 为数字化转型的重要基础设施。 01 数据平台的发展历程…...
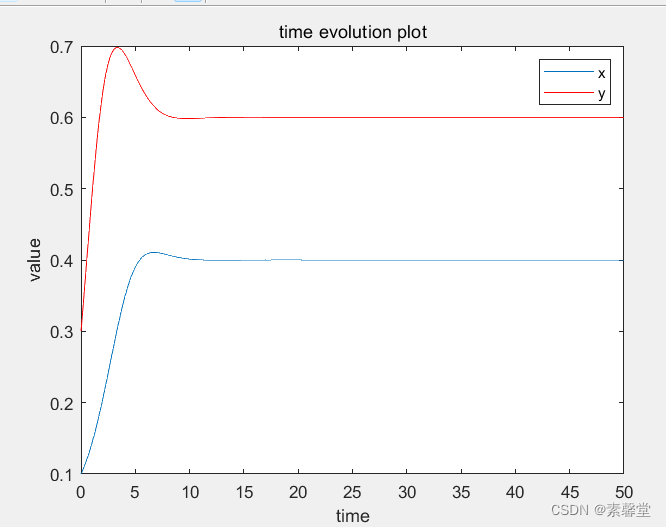
40.利用欧拉法求解微分方程组(matlab程序)
1.简述 求解微分方程的时候,如果不能将求出结果的表达式,则可以对利用数值积分对微分方程求解,获取数值解。欧拉方法是最简单的一种数值解法。前面介绍过MATLAB实例讲解欧拉法求解微分方程,今天实例讲解欧拉法求解一阶微分方程组。…...

OpenAI-Translator 实战总结
最近在极客时间学习《AI 大模型应用开发实战营》,自己一边跟着学一边开发了一个进阶版本的 OpenAI-Translator,在这里简单记录下开发过程和心得体会,供有兴趣的同学参考 功能概览 通过openai的chat API,实现一个pdf翻译器实现一个…...
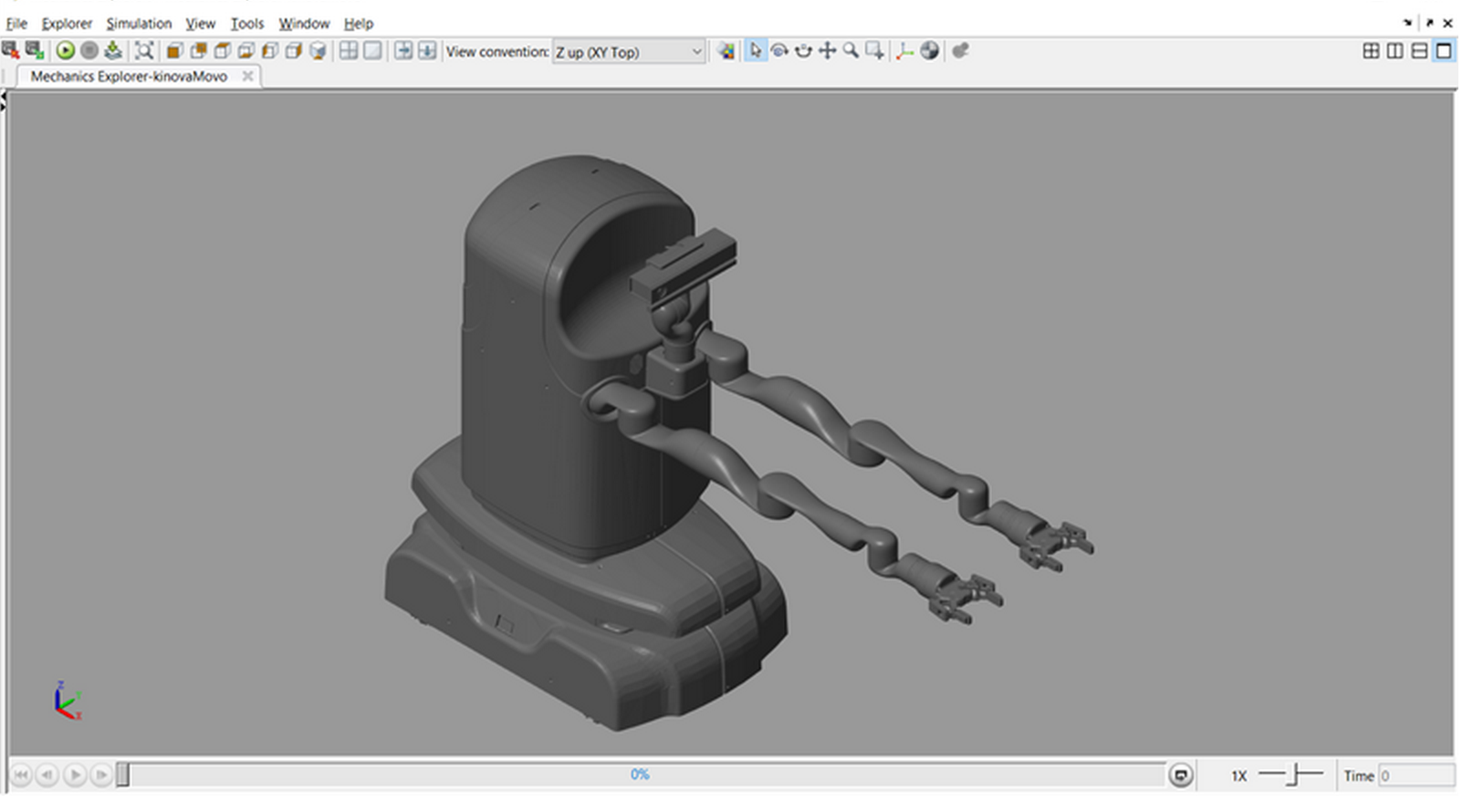
【工业机器人】用于轨迹规划和执行器分析的机械手和移动机器人模型(MatlabSimulink)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

开源在线文档服务OnlyOffice
开源在线文档服务OnlyOffice应用启动与示例运行 - 掘金 ONLYOFFICE API 文档 - Example - IDEA运行Java示例 | ONLYOFFICE中文网 NEXTCLOUDonlyoffice的搭建和使用_nextcloud onlyoffice_莫冲的博客-CSDN博客 OnlyOffice java 部署使用,文件流方式 预览文件 | 言曌博…...

汽车基本常识
目录 电源KL30KL15 零部件简称 电源 KL30 KL15 零部件简称 VCU:整车控制器 直接网络管理节点 CDU:充电系统控制器 MCU:电机控制器 TCU:变速箱控制器 ABS:防抱死系统 EPS:助力转向 T-Box:远程…...

百度资深PMO阚洁受邀为第十二届中国PMO大会演讲嘉宾
百度在线网络技术(北京)有限公司资深PMO阚洁女士受邀为由PMO评论主办的2023第十二届中国PMO大会演讲嘉宾,演讲议题:运筹于股掌之间,决胜于千里之外 —— 360斡旋项目干系人。大会将于8月12-13日在北京举办,…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

嵌入式学习之系统编程(九)OSI模型、TCP/IP模型、UDP协议网络相关编程(6.3)
目录 一、网络编程--OSI模型 二、网络编程--TCP/IP模型 三、网络接口 四、UDP网络相关编程及主要函数 编辑编辑 UDP的特征 socke函数 bind函数 recvfrom函数(接收函数) sendto函数(发送函数) 五、网络编程之 UDP 用…...

JS红宝书笔记 - 3.3 变量
要定义变量,可以使用var操作符,后跟变量名 ES实现变量初始化,因此可以同时定义变量并设置它的值 使用var操作符定义的变量会成为包含它的函数的局部变量。 在函数内定义变量时省略var操作符,可以创建一个全局变量 如果需要定义…...

文件上传漏洞防御全攻略
要全面防范文件上传漏洞,需构建多层防御体系,结合技术验证、存储隔离与权限控制: 🔒 一、基础防护层 前端校验(仅辅助) 通过JavaScript限制文件后缀名(白名单)和大小,提…...
