MATLAB实现两组数据的延时对齐效果
博主在某次实验中,相同的实验条件下分别采集了两组数据,发现两组数据存在一个延时,如下图所示:
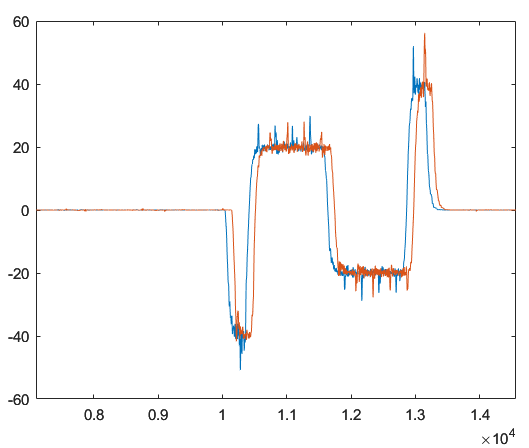
本文记录消除这个延时,实现相同数据状态的对齐效果,采用MATLAB自带的xcorr函数实现,具体步骤如下:
- step1: 导入两组数据,并将其分别存储在两个向量(例如
data1和data2)中 - step2: 使用xcorr函数计算两组数据的互相关系数,使用方法为:
xc = xcorr(data2, data1); - step3: 找到互相关系数的峰值及其位置,可以使用
findpeaks函数来查找互相关系数的峰值,然后使用max函数找到最大峰值的位置 - step4: 根据找到的延时值对
data2进行对齐,通常我们使用原数据的头或尾进行数据补齐
代码如下:
% 使用xcorr函数计算两组数据的互相关系数
xc = xcorr(data2, data1);% 找到互相关系数的峰值及其位置
[peaks, locs] = findpeaks(xc);
[~, idx] = max(peaks);
delay = locs(idx) - length(data1);% 对数据进行处理,使用第一个值或最后一个值进行数据补齐
if delay > 0data2_aligned = [data2(delay+1:end), ones(1, delay)*data2(end)];
elsedata2_aligned = [ones(1, -delay)*data2(1), data2(1:end+delay)];
end
最终实现效果如下:
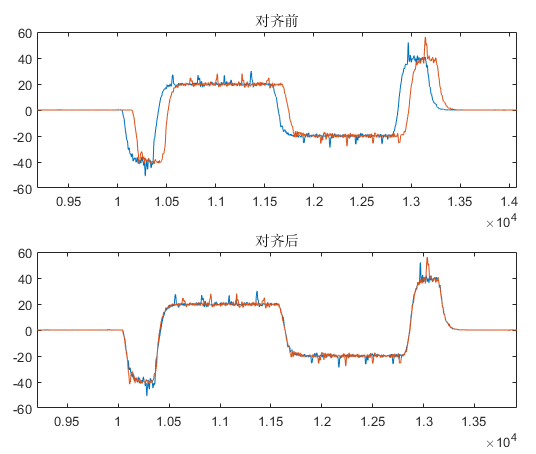
参考链接:
- https://ww2.mathworks.cn/help/matlab/ref/xcorr.html;jsessionid=ea8b98b50d13fc92e3e2d26735cb
- https://blog.csdn.net/weixin_39509073/article/details/127613031
相关文章:

MATLAB实现两组数据的延时对齐效果
博主在某次实验中,相同的实验条件下分别采集了两组数据,发现两组数据存在一个延时,如下图所示: 本文记录消除这个延时,实现相同数据状态的对齐效果,采用MATLAB自带的xcorr函数实现,具体步骤如下…...
基于Spring Boot的网络在线学习网站的设计与实现(Java+spring boot+MySQL)
获取源码或者论文请私信博主 演示视频: 基于Spring Boot的网络在线学习网站的设计与实现(Javaspring bootMySQL) 使用技术: 前端:html css javascript jQuery ajax thymeleaf 微信小程序 后端:Java spri…...

Is a directory: ‘outs//.ipynb_checkpoints‘
提示out/文件夹的.ipynp_chechpoints是一个文件夹,但是打开文件夹却没有看到,可以得知他是一个隐藏文件夹,进入outs/文件夹,使用 ls -a可以看到所有文件 果然出现这个文件夹,但是我们这个outs/文件夹存放的是图片&am…...

PintOS lab2 User Programs 实验记录
Background 大体流程如下图所示,显然这时候start_process无法被调度到。 然后start_process 里面load .out文件 (.o文件就是对象文件,是可重定向文件的一种,通常以ELF格式保存,里面包含了对各个函数的入口标记,描述,…...

『CV学习笔记』docker和nvidia-docker离线安装
docker和nvidia-docker离线安装 文章目录 1. docker的deb包下载链接2. nvidia-docker 的deb包下载3. 重启 docker4. 检验安装5. Docker容器命令行不支持Tab键命令自动补全6. 参考文献这里是ubuntu操作系统, 如果是其他的操作系统,则需要安装对应的deb包1. docker的deb包下载链…...

使用JavaScript实现页面滑动切换效果
使用JavaScript实现页面滑动切换效果 在现代Web页面设计中,页面滑动切换效果已经成为了一种常见的设计要求,能够提升用户体验,增加页面的交互性。本文将通过JavaScript来实现这一效果。 首先,我们需要在HTML中添加一些基础结构和…...

react中的formik如何使用
介绍: Formik 是一个用于处理表单状态和验证的 React 库。它提供了一种简化和统一的方式来处理复杂的表单逻辑,包括表单值的管理、表单验证、表单提交和错误处理等。 使用 安装 Formik 和 Yup(用于表单验证): // ba…...

MYSQL储存过程
一、概念及形式 存储过程就是作为可执行对象存放在数据库中的一个或多个SQL命令,通俗来讲存储过程其实就是能完成一定操作的一组SQL语句。 1、自定义语句结束符 DELIMITER $$ 2、创建 使用CREATE动作及PROCEDURE关键字进行过程创建,一般格式为&…...
fastadmin、vue、react图标库适用于多种框架
在二开fastadmin中,在写vue以及react时,侧边导航栏以及按钮中常常需要很多图标,那么这些图标应该去哪里得到呢,在这里给大家一个链接,这里有丰富的图标库,可以找到自己想要的进行使用。 点击下方链接&…...

篇七:桥接模式:连接抽象和实现
篇七:“桥接模式:连接抽象和实现” 开始本篇文章之前先推荐一个好用的学习工具,AIRIght,借助于AI助手工具,学习事半功倍。欢迎访问:http://airight.fun/。 另外有2本不错的关于设计模式的资料,…...

STL容器适配器 -- stack和queue(使用+实现)(C++)
stack和queue stackstack的介绍stack的使用stack的实现 queuequeue的介绍queue的使用queue的实现 deque简单介绍deque(双端队列)双开口连续打引号的原因 deque底层结构deque的迭代器封装结构(复杂)deque的优缺点 栈和队列数据结构…...

K8s operator从0到1实战
Operator基础知识 Kubernetes Operator是一种用于管理和扩展Kubernetes应用程序的模式和工具。它们是一种自定义的Kubernetes控制器,可以根据特定的应用程序需求和业务逻辑扩展Kubernetes功能。 Kubernetes Operator基于Kubernetes的控制器模式,通过自…...

【LangChain学习】基于PDF文档构建问答知识库(三)实战整合 LangChain、OpenAI、FAISS等
接下来,我们开始在web框架上整合 LangChain、OpenAI、FAISS等。 一、PDF库 因为项目是基于PDF文档的,所以需要一些操作PDF的库,我们这边使用的是PyPDF2 from PyPDF2 import PdfReader# 获取pdf文件内容 def get_pdf_text(pdf):text "…...

阿里云国际站对象储存OSS的常见问题?
1.什么是阿里云OSS? 阿里云对象存储服务OSS(Object Storage Service),是阿里云提供的海量、安全、低成本、高持久性的云存储服务,并可无限扩展。其数据设计持久性不低于99.9999999999%(12个9)&a…...
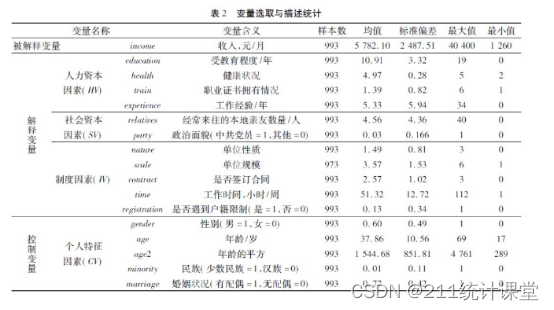
spss什么是描述性分析,以及如何去处理。
描述性分析是数据分析的第一步,是了解和认识数据基本特征和结构的方法,只有在完成了描述性统计分析,充分的了解和认识数据特征后,才能更好地开展后续更复杂的数据分析。因此,描述性分析是开展数据分析过程中最基础且必…...
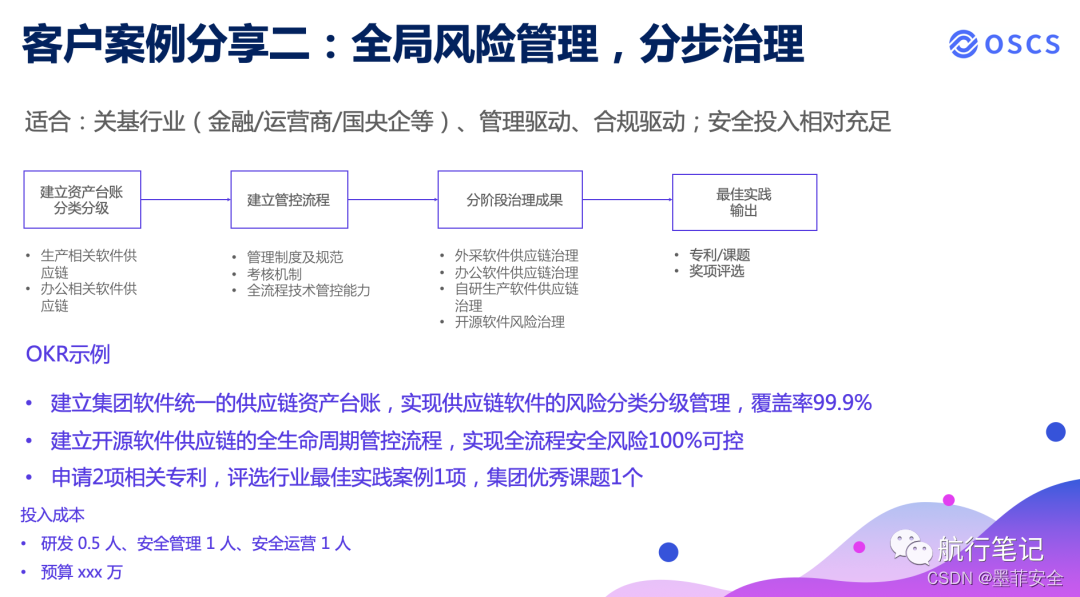
OSCS 闭门研讨第一期实录:软件供应链安全建设价值
2023 年 7 月 18 日晚 19:30,软件供应链安全技术交流群(OSCS)组织了第一次线上的闭门研讨会,本次研讨会我们收到 71 个来自各个企业关注软件供应链安全的技术专家的报名,根据研讨会参与规则要求,我们对报名…...
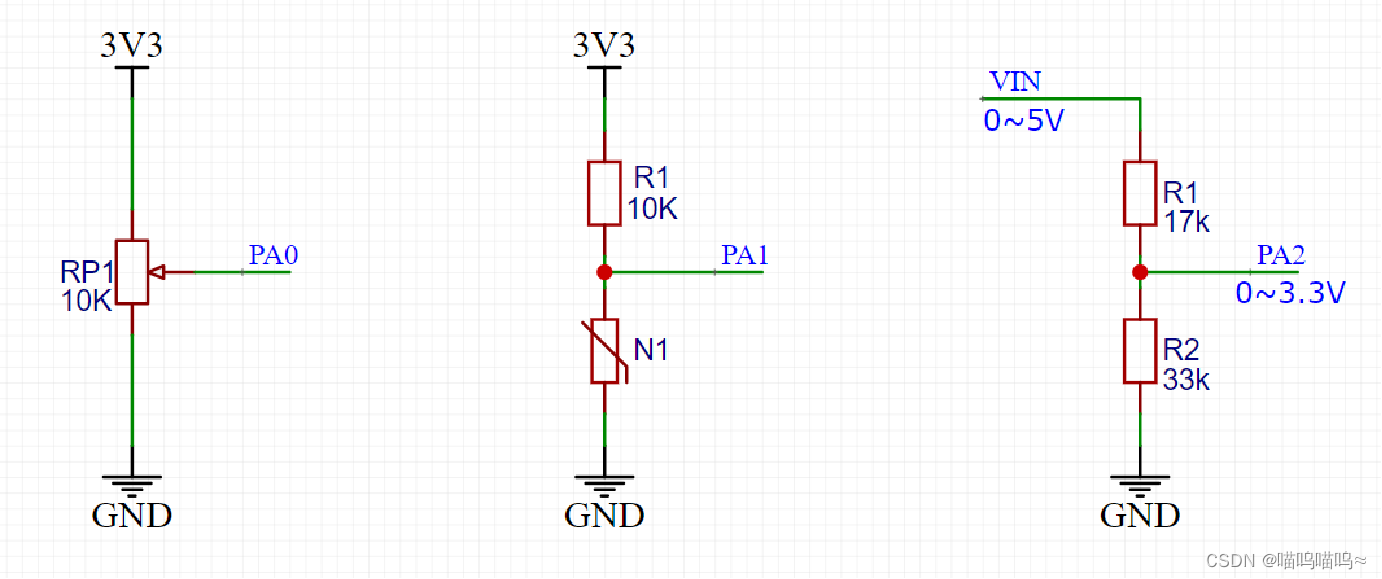
STM32入门——ADC模数转换
ADC简介 ADC(Analog-Digital Converter)模拟-数字转换器ADC可以将引脚上连续变化的模拟电压转换为内存中存储的数字变量,建立模拟电路到数字电路的桥梁12位逐次逼近型ADC,1us转换时间输入电压范围:0~3.3V,…...
)
【Fegin技术专题】「原生态」打开Fegin之RPC技术的开端,你会使用原生态的Fegin吗?(下)
内容简介 在项目开发中,除了考虑正常的调用之外,负载均衡和故障转移也是关注的重点,这也是feign ribbon的优势所在,基于上面两篇文章的基础,接下来我们开展最后一篇原生态fegin结合ribbon服务进行服务远程调用且实现负…...
)
【leetcode】454. 四数相加 II(medium)
给你四个整数数组 nums1、nums2、nums3 和 nums4 ,数组长度都是 n ,请你计算有多少个元组 (i, j, k, l) 能满足: 0 < i, j, k, l < nnums1[i] nums2[j] nums3[k] nums4[l] 0 思路:如果要暴力,那么时间复杂…...

PHP先等比缩放再无损裁剪图片【实例源码】
很多人在使用程序裁剪图片时,是在原图上直接裁剪,这样的裁剪结果是使得图片变得不完整了,理想的做法是先等比缩小图片,再把多余的部分裁掉,这样会保留更多的图片信息。 实现代码: <?php/*** 说明:函数功能是把一个图像裁剪为任意大小的图像,图像不变形** @param …...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...
