【深入浅出程序设计竞赛(基础篇)第一章 算法小白从0开始】
深入浅出程序设计竞赛(基础篇)第一章 算法小白从0开始
- 第一章 例题
- 例1-1
- 例1-2
- 例1-3
- 例1-4
- 例1-5
- 例1-6
- 例1-7
- 例1-8
- 例1-9
- 例1-10
- 例1-11
- 第一章 课后习题
- 1-1
- 1-2
- 1-3
- 1-4
第一章 例题
例1-1
#include<iostream>
using namespace std;int main(){cout << "I love Lugou !";return 0;
}
例1-2
#include<iostream>
using namespace std;int main(){cout << 2 + 4 << " " << 10 - 2 - 4 ;return 0;
}
例1-3
#include<iostream>
using namespace std;int main(){cout << 14 / 4 << endl; // 向下取整为3cout << 14 / 4 * 4 << endl;cout << 14 % 4 << endl;return 0;
}
例1-4
#include<iostream>
using namespace std;int main(){cout << 500.0 / 3 << endl; //整数 加减乘除模 还是 整数,浮点数 加减乘除模 是 小数return 0;
}
例1-5
#include<iostream>
using namespace std;int main(){cout << 500.0 / 3 << endl; // cout输出浮点数默认保留不超过6位有效数字,如果数字过大或过小就会使用科学计数法输出。同样保留不超过6位有效数字cout << 5000000.0 / 3 << endl;cout << 0.000005 / 3 << endl;cout << 5e6 / 3 + 5e-6 / 3 - 5e6 / 3 << endl; //计算机的存储方式决定了浮点数能够表示的精度是有限的,后面章节会讨论return 0;
}
例1-6
#include<iostream>
using namespace std;int main(){//假设甲车是静止的,那么乙车的总路程为 260 + 220,乙车的车速为 (12 + 20) /scout << ( 260 + 220 ) / ( 12 + 20 ) << endl;return 0;
}
例1-7
#include<iostream>
#include<cmath> //sqrt()、pow()两个函数与这个库有关
using namespace std;int main(){cout << pow(6, 2) << endl; //书中说返回的是浮点数,但是输出的值为36是整数,可能小数点自动省略了?cout << sqrt(pow(6, 2) + pow(9, 2)) << endl;return 0;
}// cmath库中的常用数学函数
//double sin(double x) 正弦
//double cos(double x) 余弦
//double exp(double x) 指数
//double log(double x) 对数
//double pow(double x, double y) 多次方
//double sqrt(double x) 算数平方根
//double fabs(double x) 绝对值
//double ceil(double x) 上整数 >=x
// double floor(double x) 下整数 <=x例1-8
#include<iostream>
using namespace std;int main(){int balance = 100; //初始余额balance = balance + 10;cout << balance << endl;balance -= 20;cout << balance << endl;balance = 0;cout << balance << endl;return 0;
}
例1-9
#include<iostream>
#include<cmath>
using namespace std;int main(){double r = 5;const double PI = 3.141593; //定义常量,一经定义在程序运行中无法修改,习惯将常量名用大写字母定义//#define PI 3.141593 这种方法定义常量无需确定其数据类型cout << 2 * PI * r << endl;cout << PI * r * r << endl;cout << PI * r * r << endl;cout << 4.0 / 3 * PI * pow(r, 3) << endl; //不能写成 4/3*PI*pow(r, 3)return 0;
}
例1-10
#include<iostream>
using namespace std;int main(){int num = 1; //第四天num = ( num + 1) * 2; //第三天num = (num + 1) * 2; //第二天num = (num + 1) * 2; //第一天cout << num << endl; return 0;
}
例1-11
(选读)评测机队列。洛谷的评测任务是单位时间内均匀增加的。8台测评机30min可以刚好把测评队列中的程序评测完毕,10台测评机6min可以刚好把测评队列中的程序评测完毕。请问“几台评测机可以在10min时刚好把评测队列中的程序评测完毕?
分析: 这是著名的“牛吃草问题”的模型。假设1台评测机1min可以评测1份程序。
首先需要分析每分钟有多少新程序进入评测队列。8台评测机30min可以评测240份,而10台评测机6min可以评测60份,可以得到30min-6min=24min内,增长了240份-60份=180份程序。因此,每分钟程序的增长速度是(240-60)/(30-6) = 7.5份/min。
6min可以评测60份,其中6 * 7.5 = 45份是新提交的程序,原有队列里面有60-45=15份程序。评测机10min一共需要评测15+10*7.5=90份程序,所以需要90/10=9台。根据这个思路,可以写出如下程序:
#include<iostream>
using namespace std;//有点难,直接看答案了
int main(){int n1 = 8, t1 = 30, n2 = 10, t2 = 6;//题目给出的评测机数量和时间int t3 = 10; //题目要求的时间double inc_rate = (1.0 * n1 * t1 - n2 * t2) / (t1 - t2); // 增长速度double init_num = n2 * t2 - inc_rate * t2; //初始队列长度double ans = (init_num + t3 * inc_rate) / t3; //求得答案cout << ans; return 0;
}
这个问题相比于前面的问题来说比较复杂,很难使用一个表达式来直接求得结果。可以把一个大人物拆分成若干规模比较小的任务,抽丝剥茧,逐步击破,直到求得最终的答案。
补充:牛吃草问题
有一片青草地,每天都匀速地长出青草,这片青草可供27头牛吃6周或供23头牛吃9周,那么这片草地可供21头牛吃几周?
#include<iostream>
using namespace std;int main(){//假设每头牛每周吃1棵草int n1 = 27, t1 = 6, n2 = 23, t2 = 9;int n3 = 21; //题目给的牛的数量double inc_rate = (1.0 * n2 * t2 - n1 * t1) / (t2 - t1); // 每周草的增长速度double init_num = n1* t1 - inc_rate * t1; //初始草的数量// 21头牛分为15把每周增长的草吃掉,那么只需直到剩下的6头把初始的草吃掉需要多长时间即可double ans = init_num / (n3 - inc_rate); //求得答案cout << ans; return 0;
}
第一章 课后习题
1-1
(1) 3 * x + 5 * y
(2) (c + 1) / (a * b)
(3) sqrt(3 * pow(a, 3))
(4) (n + 2) * (n - 9)
1-2
//C++变量命名规则
// 1、 变量名只能是字母(A-Z,a-z)和数字(0-9)或者下划线(_)组成。
// 2、 第一个字母必须是字母或者下划线开头。
// 3、 不能使用C++关键字来命名变量,以免冲突。
// 4、 变量名区分大小写。(1) kkksc03 合法
(2) OhILoveLuoguVeryMuchAndIWiIIStudy 合法(但是名称太长了)
(3) _1apple 合法
(4) char 不合法 关键字
(5) kkk@SH 不合法 含有@
(6) a 合法
(7) iPhone 合法
(8) 11dimensions 不合法 以数字开头
(9) __stdcall 不合法,是函数
1-3
1-4
#include<iostream>
using namespace std;int main(){cout << 3.0 / 3 / 3 * 9 * 9 << endl; //1cout << ((24 - 4) / 2) * ((24 - 4) / 2 + 4) << endl; //2cout << 480 / (1.4 + 1) << " " << 480 / (1.4 + 1) * 1.4 << endl; //3cout << 11 + 1 << " " << 3 * (11 + 1) + 11 << endl; //4cout << 80 * 12 / (120 - 80) << endl; //5int x = (94 - 35 * 2) / 2 ; int y = 35 - x; cout << x << " " << y << endl; //6double a = 10000 * (1 + 0.035) * (1 + 0.035) * (1 + 0.035) * (1 + 0.035) * (1 + 0.035);double b = 10000 * (1 + 0.04);cout << a << " " << b << endl;return 0;
}
相关文章:
第一章 算法小白从0开始】)
【深入浅出程序设计竞赛(基础篇)第一章 算法小白从0开始】
深入浅出程序设计竞赛(基础篇)第一章 算法小白从0开始 第一章 例题例1-1例1-2例1-3例1-4例1-5例1-6例1-7例1-8例1-9例1-10例1-11 第一章 课后习题1-11-21-31-4 第一章 例题 例1-1 #include<iostream> using namespace std;int main(){cout <&…...

openGauss学习笔记-36 openGauss 高级数据管理-TRUNCATE TABLE语句
文章目录 openGauss学习笔记-36 openGauss 高级数据管理-TRUNCATE TABLE语句36.1 语法格式36.2 参数说明36.3 示例 openGauss学习笔记-36 openGauss 高级数据管理-TRUNCATE TABLE语句 清理表数据,TRUNCATE TABLE用于删除表的数据,但不删除表结构。也可以…...

ChatGPT生成文本检测器算法挑战大赛
ChatGPT生成文本检测器算法挑战大 比赛链接:2023 iFLYTEK A.I.开发者大赛-讯飞开放平台 (xfyun.cn) 1、数据加载和预处理 import numpy as np import pandas as pd from sklearn.model_selection import train_test_split, cross_val_predict from sklearn.linea…...
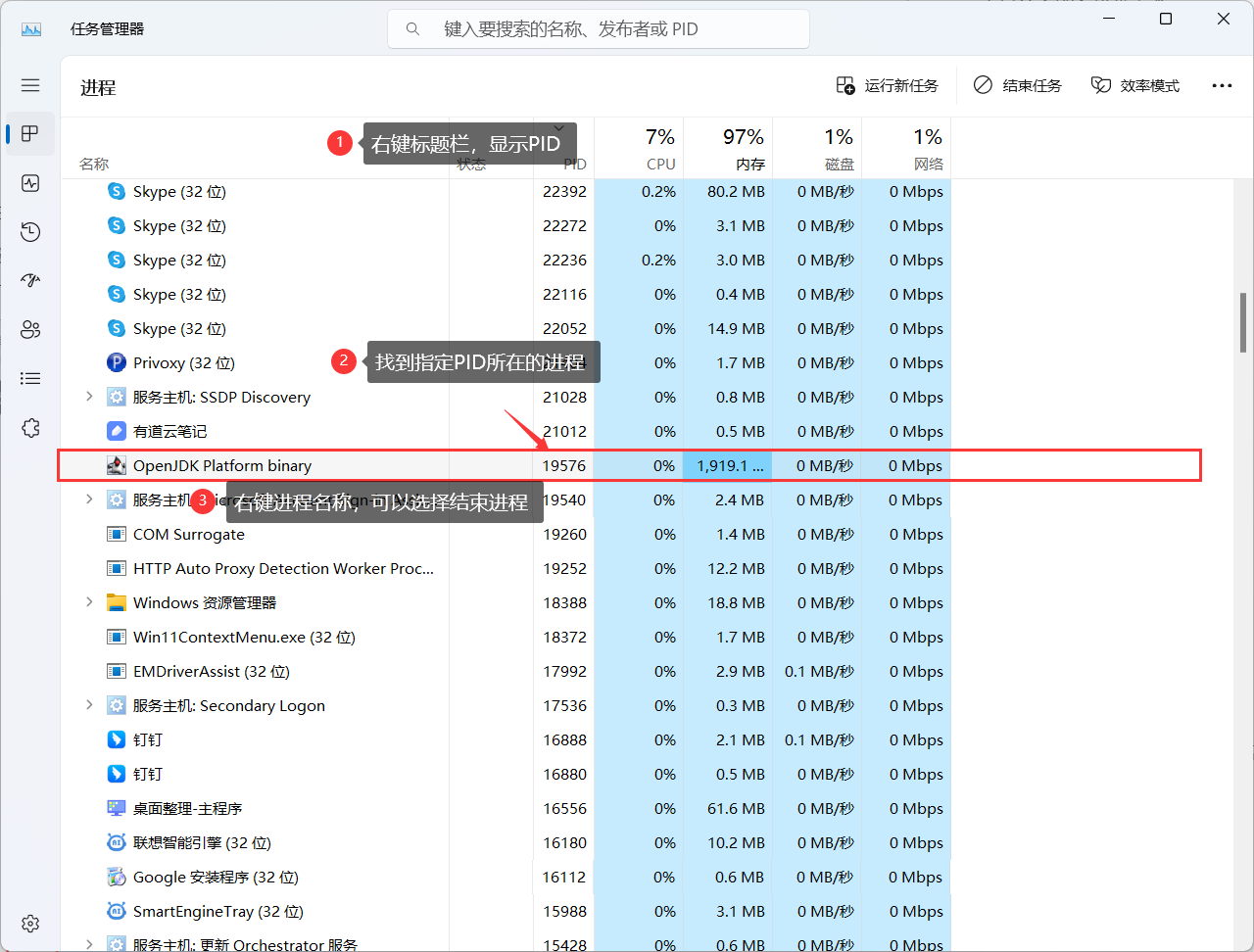
O2OA开发平台实施入门指南
O2OA(翱途)开发平台,是一款适用于协同办公系统开发与实施的基础平台,说到底,它也是一款快速开发平台。开发者可以基于平台提供的能力完成门户、流程、信息相关的业务功能开发。 既然定位为开发平台,那么开…...

服装行业多模态算法个性化产品定制方案 | 京东云技术团队
一、项目背景 AI赋能服装设计师,设计好看、好穿、好卖的服装 传统服装行业痛点 • 设计师无法准确捕捉市场趋势,抓住中国潮流 • 上新周期长,高库存滞销风险大 • 基本款居多,难以满足消费者个性化需求 解决方案 • GPT数据…...

MySQL表空间结构与页、区、段的定义
文章目录 一、概念引入1、页2、区3、段 二、页的结构1、File Header2、FIle Trailer 三、区的结构1、分类2、XDES Entry3、XDES Entry链表 四、段的结构五、独立表空间1、FSP_HDR页2、XDES页3、IBUF_BITMAP页4、INODE页5、INDEX页 六、系统表空间 一、概念引入 1、页 InnoDB是…...
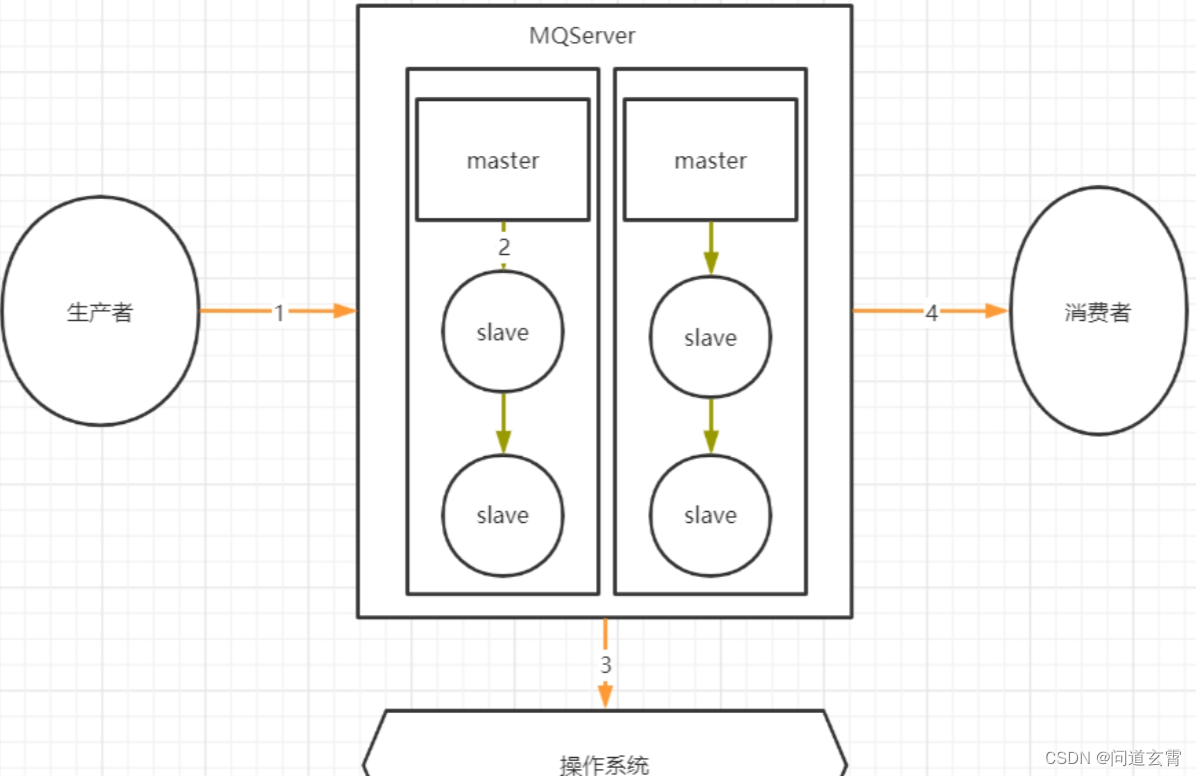
RaabitMQ(三) - RabbitMQ队列类型、死信消息与死信队列、懒队列、集群模式、MQ常见消息问题
RabbitMQ队列类型 Classic经典队列 这是RabbitMQ最为经典的队列类型。在单机环境中,拥有比较高的消息可靠性。 经典队列可以选择是否持久化(Durability)以及是否自动删除(Auto delete)两个属性。 Durability有两个选项,Durable和Transient。 Durable表…...

Unity3D GPU Selector/Picker
Unity3D GPU Selector/Picker 一、概述 1.动机 Unity3D中通常情况下使用物理系统进行物体点击选择的基础,对于含大量对象的场景,添加Collider组件会增加内容占用,因此使用基于GPU的点击选择方案 2.实现思路 对于场景的每个物体,…...
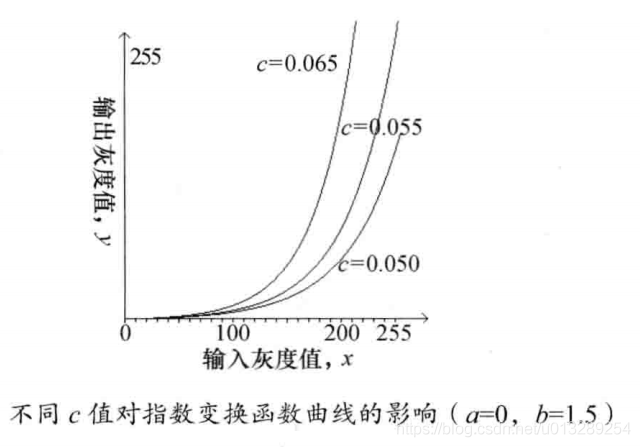
灰度非线性变换之c++实现(qt + 不调包)
本章介绍灰度非线性变换,具体内容包括:对数变换、幂次变换、指数变换。他们的共同特点是使用非线性变换关系式进行图像变换。 1.灰度对数变换 变换公式:y a log(1x) / b,其中,a控制曲线的垂直移量;b为正…...

轻量级Web框架Flask
Flask-SQLAlchemy MySQL是免费开源软件,大家可以自行搜索其官网(https://www.MySQL.com/downloads/) 测试MySQL是否安装成功 在所有程序中,找到MySQL→MySQL Server 5.6下面的命令行工具,然后单击输入密码后回车&am…...

【gridsample】地平线如何支持gridsample算子
文章目录 1. grid_sample算子功能解析1.1 理论介绍1.2 代码分析1.2.1 x,y取值范围[-1,1]1.2.2 x,y取值范围超出[-1,1] 2. 使用grid_sample算子构建一个网络3. 走PTQ进行模型转换与编译 实操以J5 OE1.1.60对应的docker为例 1. grid_sample算子功能解析 该段主要参考:…...
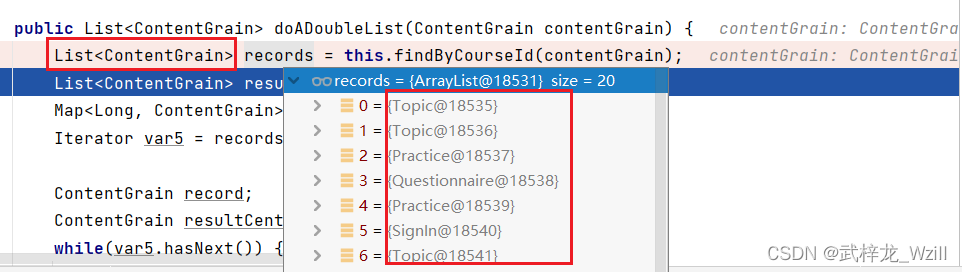
JPA实现存储实体类型信息
本文已收录于专栏 《Java》 目录 背景介绍概念说明DiscriminatorValue 注解:DiscriminatorColumn 注解:Inheritance(strategy InheritanceType.SINGLE_TABLE) 注解: 实现方式父类子类执行效果 总结提升 背景介绍 在我们项目开发的过程中经常…...

阿里云快速部署开发环境 (Apache + Mysql8.0+Redis7.0.x)
本文章的内容截取于云服务器管理控制台提供的安装步骤,再整合前人思路而成,文章末端会提供原文连接 ApacheMysql 8.0部署MySQL数据库(Linux)步骤一:安装MySQL步骤二:配置MySQL步骤三:远程访问My…...
语音秘书:让录音转文字识别软件成为你的智能工作助手
每当在需要写文章的深夜,我的思绪经常跟不上我的笔,即便是说出来用录音机录下,再书写出来,也需要耗费大量时间。这个困扰了我很久的问题终于有了解决的办法,那就是录音转文字软件。它像个语言魔术师,将我所…...
【腾讯云 Cloud Studio 实战训练营】用于编写、运行和调试代码的云 IDE泰裤辣
文章目录 一、引言✉️二、什么是腾讯云 Cloud Studio🔍三、Cloud Studio优点和功能🌈四、Cloud Studio初体验(注册篇)🎆五、Cloud Studio实战演练(实战篇)🔬1. 初始化工作空间2. 安…...

[C#] 简单的俄罗斯方块实现
一个控制台俄罗斯方块游戏的简单实现. 已在 github.com/SlimeNull/Tetris 开源. 思路 很简单, 一个二维数组存储当前游戏的方块地图, 用 bool 即可, true 表示当前块被填充, false 表示没有. 然后, 抽一个 “形状” 类, 形状表示当前玩家正在操作的一个形状, 例如方块, 直线…...
postman官网下载安装登录详细教程
目录 一、介绍 二、官网下载 三、安装 四、注册登录postman账号(不注册也可以) postman注册登录和不注册登录的使用区别 五、关于汉化的说明 一、介绍 简单来说:是一款前后端都用来测试接口的工具。 展开来说:Postman 是一个…...

(贪心) 剑指 Offer 14- I. 剪绳子 ——【Leetcode每日一题】
❓剑指 Offer 14- I. 剪绳子 难度:中等 给你一根长度为 n 的绳子,请把绳子剪成整数长度的 m 段(m、n都是整数,n > 1 并且 m > 1),每段绳子的长度记为 k[0],k[1]...k[m-1] 。请问 k[0]*k[1]*...*k[m…...
如何将Linux上的cpolar内网穿透设置成 - > 开机自启动
如何将Linux上的cpolar内网穿透设置成 - > 开机自启动 文章目录 如何将Linux上的cpolar内网穿透设置成 - > 开机自启动前言一、进入命令行模式二、输入token码三、输入内网穿透命令 前言 我们将cpolar安装到了Ubuntu系统上,并通过web-UI界面对cpolar的功能有…...
)
50.两数之和(力扣)
目录 问题描述 核心代码解决 代码思想 时间复杂度和空间复杂度 问题描述 给定一个整数数组 和一个整数目标值 ,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。numstarget 你可以假设每种输入只会对应一个答案。但是&am…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...
