力扣(LeetCode)240. 搜索二维矩阵 II(C++)
题目描述
枚举
枚举整个矩阵,找到等于 target 的元素,则 return true ,否则 return false。
class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {int n = matrix.size(), m = matrix[0].size();for (auto &x : matrix)for (auto &t : x)if (t == target) return true;return false;}
};
- 时间复杂度 : O(n×m)O(n\times m)O(n×m) , nnn 是数组的行数,mmm 是数组的列数,枚举所有元素,时间复杂度 O(n×m)O(n\times m)O(n×m) 。
- 空间复杂度 : O(1)O(1)O(1) , 只使用常量级空间 。
二分查找
二分优化枚举。按行枚举矩阵,由于每行元素有序,可以二分查找行内的元素。
class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {int n = matrix.size(), m = matrix[0].size();for (auto &x : matrix) {int l = 0, r = m - 1;while(l <= r) {int mid = l + (r - l >> 1);if (x[mid] < target) l = mid + 1;else r = mid - 1;}if (l < m && x[l] == target) return true;}return false;}
};
- 时间复杂度 : O(nlogm)O(nlogm)O(nlogm) , nnn 是数组的行数,mmm 是数组的列数,一次枚举一行,每行二分查找,时间复杂度 O(nlogm)O(nlogm)O(nlogm) 。
- 空间复杂度 : O(1)O(1)O(1) , 只使用常量级空间 。
枚举行列
更大胆的,同时枚举行列。这是由于每行元素有序,每列元素同样有序。
目的:保证被枚举元素与 target 的大小关系,对应唯一的移动方向
结论:从右上角枚举到左下角,根据右上角元素与 target 的大小关系,确定枚举的移动方向。
证明:右上角元素是一行的最大元素,一列的最小元素。往左下枚举,要找比他小的元素,只能同行往左;要找比他大的元素,只能同列向下。即
右上角元素 >\gt> target,往左;右上角元素 <\lt< target,往下。
朴素错法
- 为什么从左上角枚举到右下角不行?
答:左上角元素是一行的最小元素,一列的最小元素。往右下枚举,要找比他大的元素,不能确定往右还是往下。
class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {int n = matrix.size(), m = matrix[0].size();int i = 0, j = m - 1;while(i < n && j >= 0) {if (matrix[i][j] > target) j --;else if (matrix[i][j] < target) i ++;else return true;}return false;}
};
- 时间复杂度 : O(n+m)O(n+m)O(n+m) , nnn 是数组的行数,mmm 是数组的列数,一次枚举,移动一列或者一行,时间复杂度 O(n+m)O(n+m)O(n+m) 。
- 空间复杂度 : O(1)O(1)O(1) , 只使用常量级空间 。
AC
按行列枚举,执行结果。

致语
- 理解思路很重要
- 读者有问题请留言,清墨看到就会回复的。
相关文章:

力扣(LeetCode)240. 搜索二维矩阵 II(C++)
题目描述 枚举 枚举整个矩阵,找到等于 target 的元素,则 return true ,否则 return false。 class Solution { public:bool searchMatrix(vector<vector<int>>& matrix, int target) {int n matrix.size(), m matrix[0]…...

golang defer
文章目录延迟函数的参数在defer语句出现时就已经确定下来了延迟函数没有入参时,延迟函数体内的变量会受到影响延迟函数 *可以* 修改主函数的 *具名* 返回值延迟函数 *无法* 修改主函数的 *匿名* 返回值defer会把声明的 延迟函数以及 函数的入参放到栈上,…...
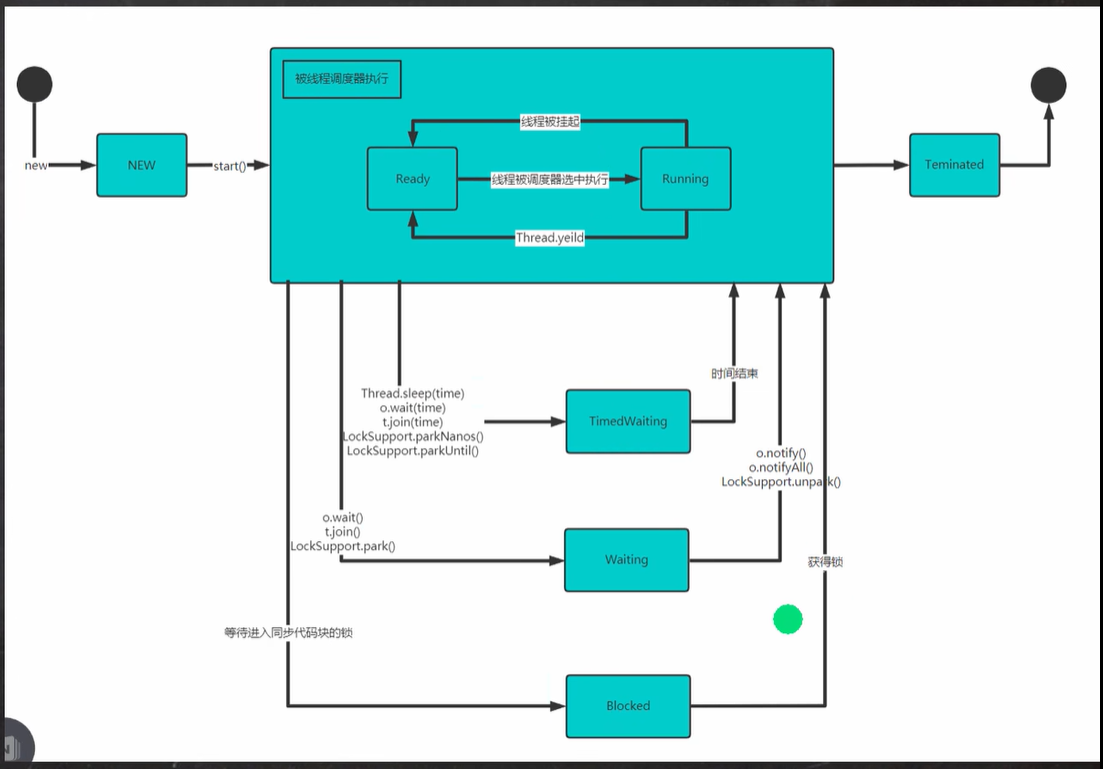
【Java】线程的死锁和释放锁
线程死锁是线程同步的时候可能出现的一种问题 文章目录1. 线程的死锁1.1 基本介绍1.2 应用案例2. 释放锁2.1 下面的操作会释放锁2.2 下面的操作不会释放锁1. 线程的死锁 1.1 基本介绍 多个线程都占用了对方的锁资源,但不肯相让,导致了死锁,…...
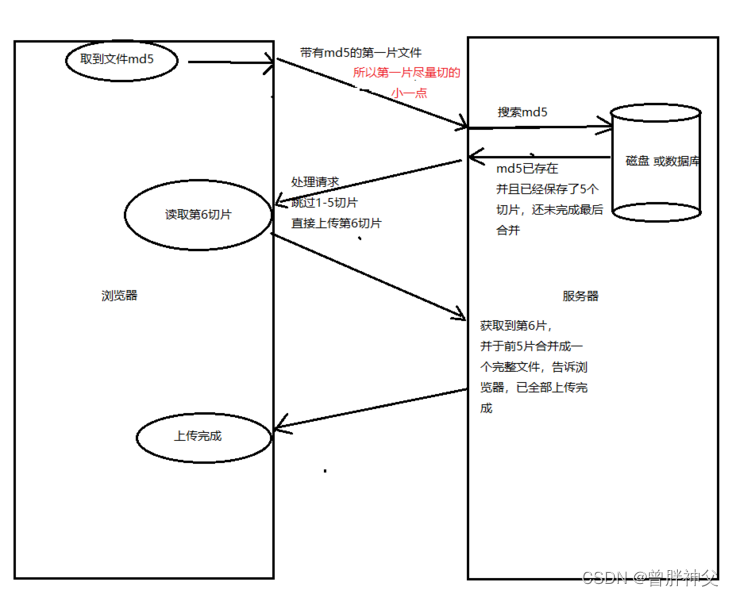
如何使用断点续传上传大文件
概念 大文件上传的需求介绍 不管怎样简单的需求,在量级达到一定层次时,都会变得异常复杂。 文件上传简单,文件变大就复杂 上传大文件时,以下几个变量会影响我们的用户体验 服务器处理数据的能力请求超时网络波动 上传时间会变长…...
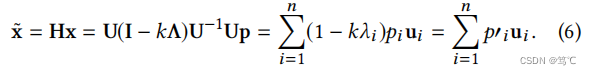
【图神经网络】图拉普拉斯滤波器如何实现全通、低通、高通滤波
【图神经网络】图拉普拉斯滤波器如何实现全通、低通、高通滤波 文章目录【图神经网络】图拉普拉斯滤波器如何实现全通、低通、高通滤波1. 前言2. 符号说明3. 三种滤波3.1 全通滤波3.2 低通滤波3.2.1 平滑信号分析3.2.2 广义拉普拉斯平滑滤波器3.3 高通滤波4. 总结1. 前言 GCN&…...

python操作mysql数据库详解
使用Python操作MySQL数据库 MySQL是一种关系型数据库管理系统,它可以用来存储和管理大量的数据。之前介绍了大部分主流数据库,今天将介绍如何使用Python来操作MySQL数据库。 安装MySQL 首先,我们需要安装MySQL服务器,可以从MyS…...
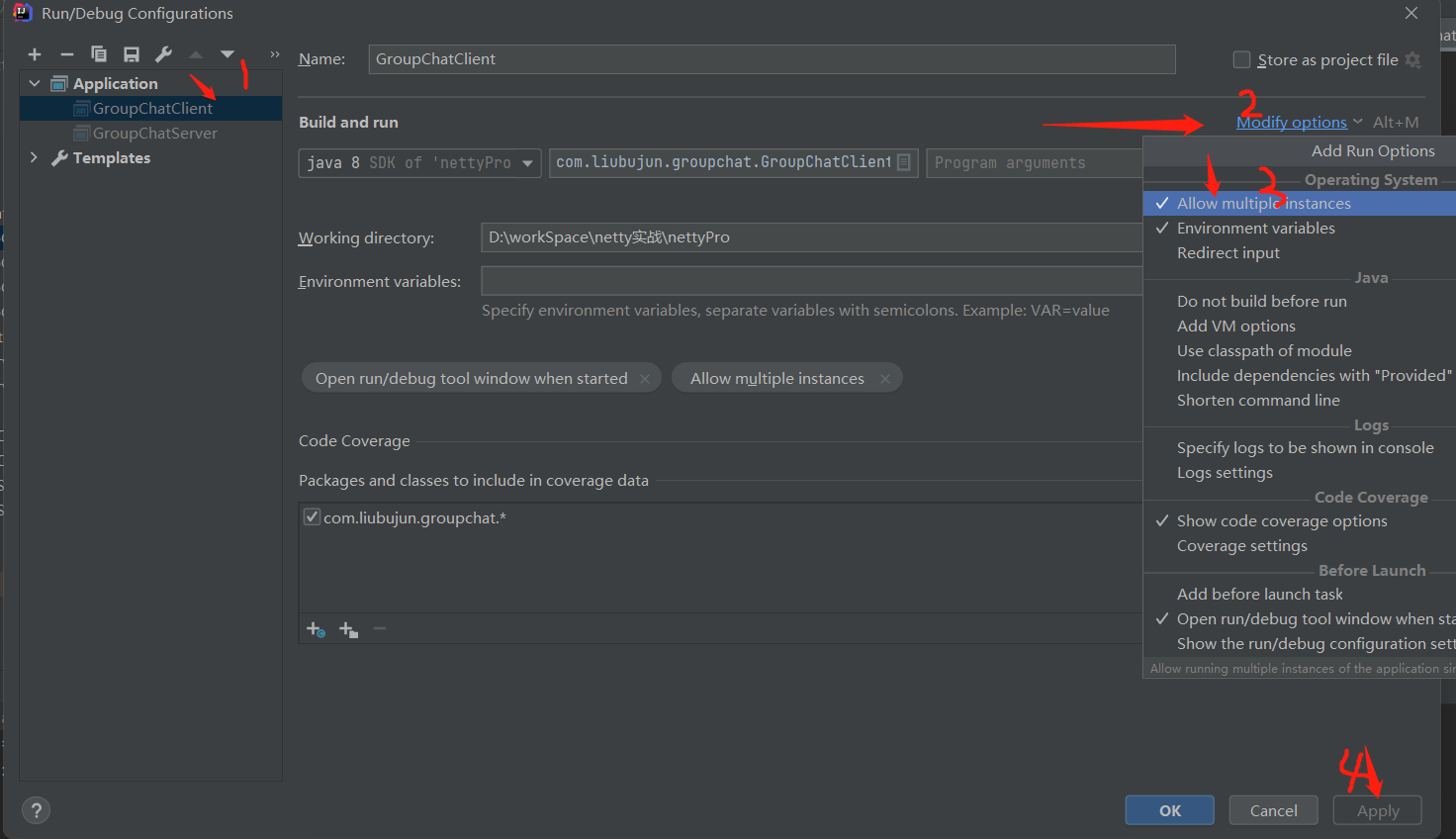
netty群聊系统
1设计思路:启动一个服务端,多个客户端第一个客户端启动时,会告诉服务器上线了第二个客户端启动时,告诉服务器上线,并且通知第一个启动的客户端第三个客户端启动时,告诉服务器上线,并且通知第一个…...
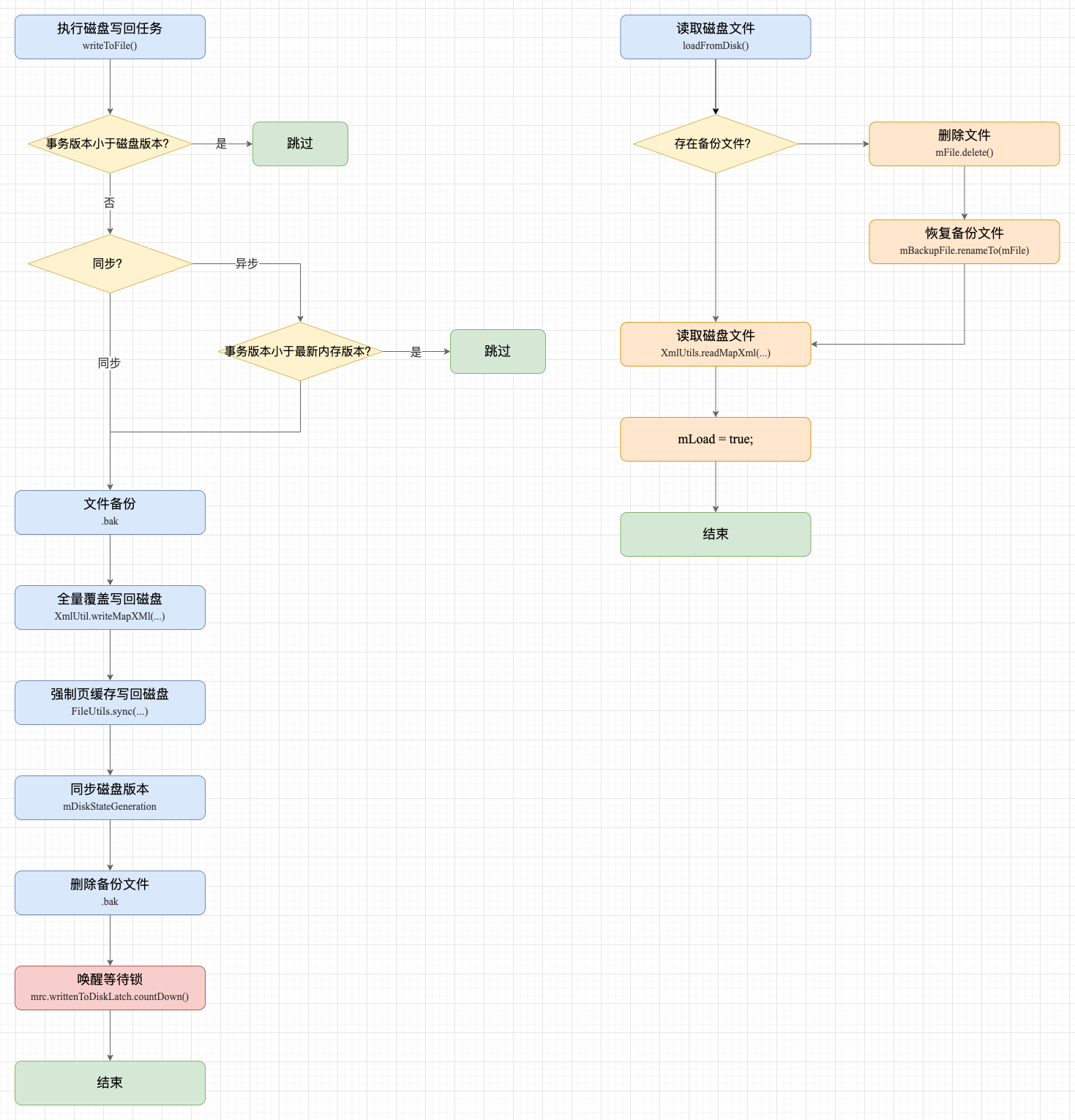
Android 初代 K-V 存储框架 SharedPreferences,旧时代的余晖?
本文已收录到 AndroidFamily,技术和职场问题,请关注公众号 [彭旭锐] 提问。 前言 大家好,我是小彭。 SharedPreferences 是 Android 平台上轻量级的 K-V 存储框架,亦是初代 K-V 存储框架,至今被很多应用沿用。 有的…...
在windows中使用tomcat搭建Jenkins
1、 准备环境:JDK JDK官网下载:https://download.oracle.com/java/19/latest/jdk-19_windows-x64_bin.msi 2、 tomcat包 tocat官网下载:https://tomcat.apache.org/download-90.cgi 3、 Jenkins.war包 Jenkins官网下载:https://mi…...

Linux系统
linux系统 世界上最重要的服务器端操作系统。 创建新目录 mkdir app mkdir -m 目录权限 目录名 创建有权限的目录名。 创建一个空白文件 touch app.txt创建一个文件。 cat创建一个文件。 vi/vim创建一个文件。 nano创建一个文件。 truncate创建一个文件。 pwd查看当前目录。 rm…...
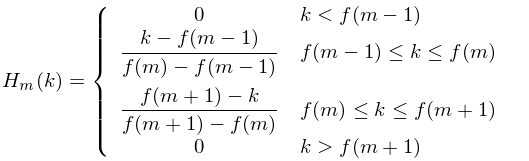
Mel Frequency Cepstral Coefficients (MFCCs)
wiki里说 在声音处理中,梅尔频率倒谱( MFC ) 是声音的短期功率谱的表示,基于非线性梅尔频率标度上的对数功率谱的线性余弦变换。 倒谱和MFC 之间的区别在于,在 MFC 中,频带在梅尔尺度上等距分布,这比正常频谱中使用的线…...
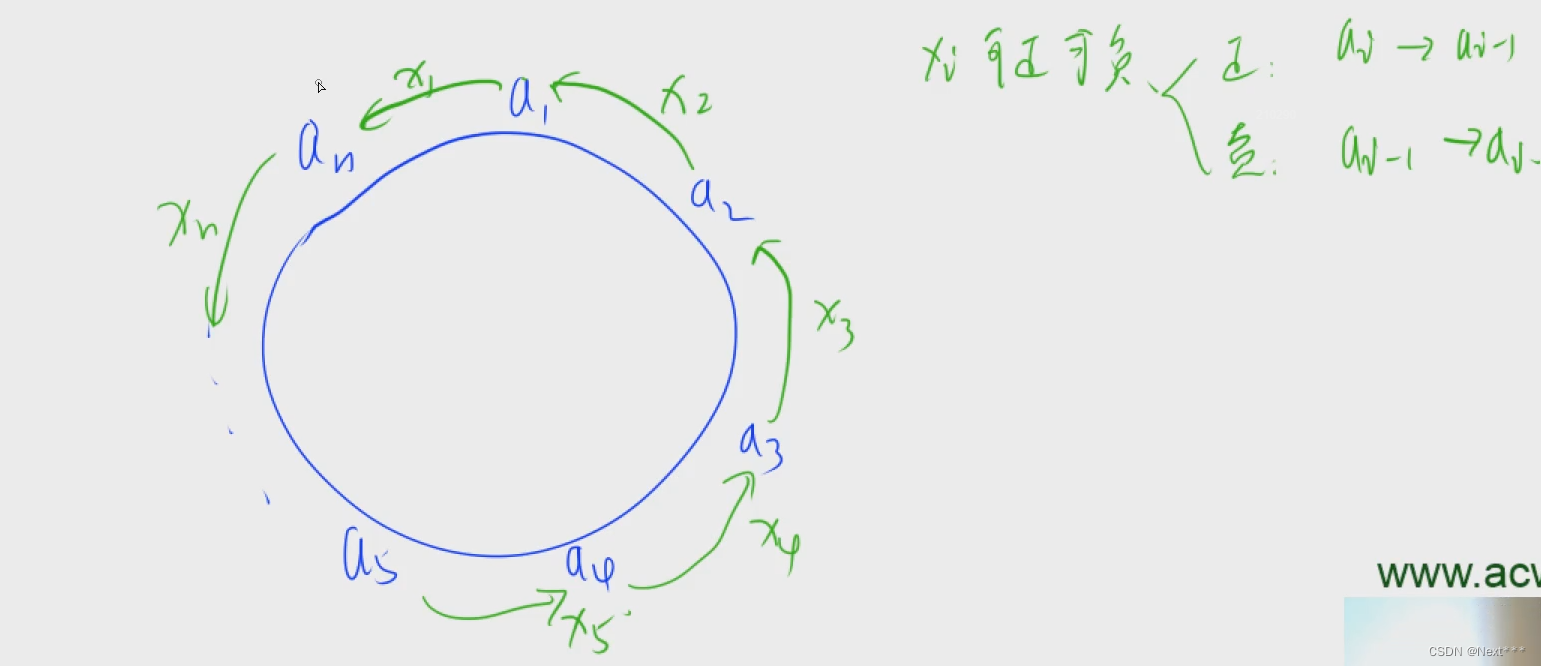
第七讲---贪心(上课)
1.股票买卖 一、贪心 考虑一种方案,在每次上升的前一天购入股票,并在上升后的当天卖出的方案 if (w[i] > w[i - 1])res w[i] - w[i - 1];接下来证明该贪心思路得出的方案即是最优解。 (1)证明贪心解 ≥ 最优解: …...

计算机如何思考与图灵完备
图灵完备是针对一套数据操作规则而言的概念,数据操作规则可以是一门编程语言,也可以是计算机实现里面的指令集,比如C/C++是图图灵完备的,通用CPU也是图灵完备的,但是GPU却不一定是图灵完备的。说白了图灵完备定义了一套规则,当这套规则可以实现图灵迹模型里的全部功能时,…...

惠普LaserJet M1005 MFP报错b2
故障现象: 惠普LaserJet M1005 MFP开机后直接报b2错误; 检测维修: 故障大意是:机器的硬件可能出现点突变,此问题建议联系当地维修中心进行处理。...
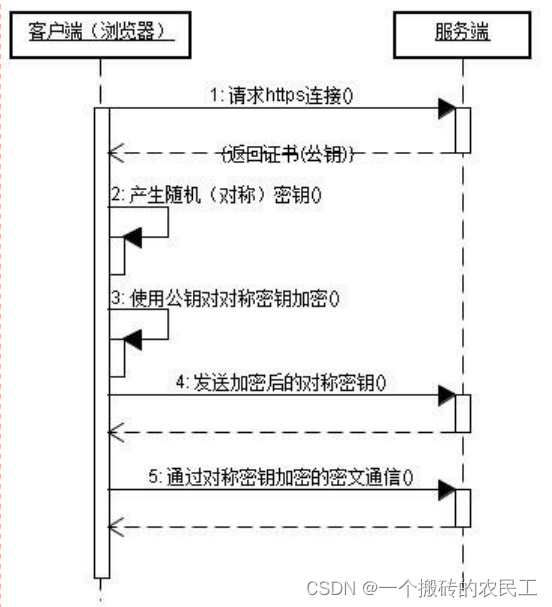
网络协议(TCP/IP)
目录一、网络分层模型二、OSI模型三、网络传输原理四、TCP/IP1、TCP/IP 原理2、TCP 三次握手/四次挥手3、Http协议和TCP/IP的区别五、HTTP原理六、HTTPS原理七、CDN原理一、网络分层模型 互联网的本质就是一系列的网络协议,最早由ISO国际组织定义为7层网络参考模型…...

2023河南省第二届职业技能大赛郑州市选拔赛“网络安全” 项目比赛样题任务书
2023河南省第二届职业技能大赛郑州市选拔赛“网络安全” 项目比赛样题任务书2023河南省第二届职业技能大赛郑州市选拔赛“网络安全” 项目比赛样题任务书A模块基础设施设置/安全加固(200分)A-1:登录安全加固(Windows, Linux&#…...

6、流程控制
目录一、if二、switch三、for四、break与continue五、goto与Label一、if if使用:逻辑表达式成立,就会执行{}里的内容;逻辑表达式不需要加() if 5 > 9 {fmt.Println("5>9") }if句子中允许包含1个(仅1个)分号:在分…...

Linux中最基本常见命令总结
❤❤💛💛💚💚💙💙💜💜您的认可是对我最大的帮助💜💜💙💙💚💚💛💛❤❤ 🤎&…...

Python学习-----模块2.0(常用模块之时间模块-->time)
目录 前言: time简介 导入模块 1.时间戳 2.时间元组 (1)把时间戳转换为元组形式 (2)元组转换为时间戳输出 (3)把元组转换为格式化时间 (4)把时间戳转换为格式化时间…...
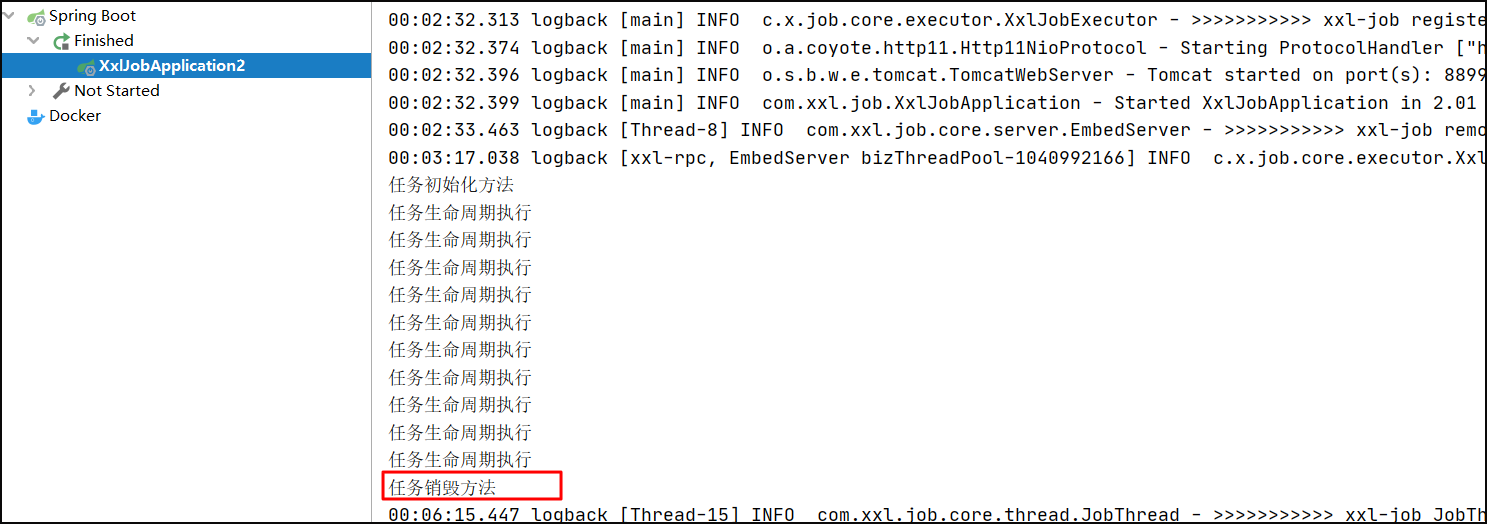
XXL-JOB分布式任务调度框架(二)-策略详解
文章目录1.引言2.任务详解2.1.执行器2.2.基础配置3.路由策略(第一个)-案例4.路由策略(最后一个)-案例5.轮询策略-案例6.随机选取7.轮询选取8.一致性hash9.最不经常使用 (LFU)10.最近最久未使用(LRU)11.故障转移12.忙碌转移13.分片广播任务14.父子任务15.…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...
