线性表中的时间复杂度
线性表
一、顺序表示的线性表
- 插入操作的时间复杂度
- 最好情况: O ( 1 ) O(1) O(1)。(新元素插到表尾,不需要移动元素)
- 最坏情况: O ( n ) O(n) O(n)。(新元素插到表头,需要将原有的n个元素全部向后移动)
- 平均情况: O ( n ) O(n) O(n)。(假设新元素插到每个位置的概率相同 ( p = 1 n + 1 ) (p=\frac{1}{n+1}) (p=n+11),则平均循环次数为 n p + ( n − 1 ) p + . . . + 1 p = n ( n + 1 ) 2 1 n + 1 = n 2 np+(n-1)p+...+1p=\frac{n(n+1)}{2}\frac{1}{n+1}=\frac{n}{2} np+(n−1)p+...+1p=2n(n+1)n+11=2n
- 删除操作
- 最好情况: O ( 1 ) O(1) O(1)。(删除表尾元素,不需要移动其他元素)
- 最坏情况: O ( n ) O(n) O(n)。(删除表头元素,需要将后序的n-1个元素全部向前移动)
- 平均情况: O ( n ) O(n) O(n)。(假设删除任何一个元素的概率相同 ( p = 1 n ) (p=\frac{1}{n}) (p=n1),则平均循环次数为 ( n − 1 ) p + ( n − 2 ) p + . . . + 1 p = n ( n − 1 ) 2 1 n = n − 1 2 (n-1)p+(n-2)p+...+1p=\frac{n(n-1)}{2}\frac{1}{n}=\frac{n-1}{2} (n−1)p+(n−2)p+...+1p=2n(n−1)n1=2n−1
- 按位查找: O ( 1 ) O(1) O(1)(由于顺序表各个数据元素在内存中连续存放,因此可以根据起始地址和数据元素大小立即找到第i个元素–“随机存取”特性)
- 按值查找:
- 最好情况: O ( 1 ) O(1) O(1)。(目标元素在表头)
- 最坏情况: O ( n ) O(n) O(n)。(目标元素在表尾)
- 平均情况: O ( n ) O(n) O(n)。(假设目标元素出现在任何一个位置的概率相同 ( p = 1 n ) (p=\frac{1}{n}) (p=n1),则平均循环次数为 1 p + 2 p + . . . + n p = n ( n + 1 ) 2 1 n = n + 1 2 1p+2p+...+np=\frac{n(n+1)}{2}\frac{1}{n}=\frac{n+1}{2} 1p+2p+...+np=2n(n+1)n1=2n+1
二、链式表示的线性表
单链表
- 插入:
- 按位序插入
- 最好情况: O ( 1 ) O(1) O(1)(插在表头)
- 最坏情况: O ( n ) O(n) O(n)(插在表尾)
- 平均情况: O ( n ) O(n) O(n)
- 指定节点的后插操作: O ( 1 ) O(1) O(1)
- 指定节点的前插操作:
- O ( n ) O(n) O(n)(循环查找指定节点p的前驱q,再对q后插)
- O ( 1 ) O(1) O(1)(若在p节点前插入s,则先将s插到p后面,再交换p和s的数据域)
- 按位序插入
- 删除:
- 按位序删除
- 最好情况: O ( 1 ) O(1) O(1)
- 最坏、平均情况: O ( n ) O(n) O(n)
- 指定节点的删除: O ( 1 ) O(1) O(1)
- 按位序删除
- 查找
- 按位查找:平均情况 O ( n ) O(n) O(n)
- 按值查找:平均情况 O ( n ) O(n) O(n)
- 求表长: O ( n ) O(n) O(n)
- 单链表的建立
- 头插法:(插入n个节点的时间复杂度为) O ( n ) O(n) O(n)
- 尾插法:
- 若不带表尾指针,则每次插入都从头遍历,时间复杂度为 O ( n 2 ) O(n^2) O(n2)
- 若设置一个表尾指针,则为 O ( n ) O(n) O(n)
双链表
与单链表一样,双链表不可随机存取,按位查找、按值查找都只能用遍历的方式实现,时间复杂度 O ( n ) O(n) O(n)
循环链表
- 从尾部找到头部,时间复杂度是 O ( 1 ) O(1) O(1);从头节点找到尾部,时间复杂度是 O ( n ) O(n) O(n)
栈
一、顺序存储实现的栈
基本操作(创建、增、删、查)都是 O ( 1 ) O(1) O(1)的时间复杂度
对于栈的销毁,在函数运行结束后由系统自动回收内存
相关文章:

线性表中的时间复杂度
线性表 一、顺序表示的线性表 插入操作的时间复杂度 最好情况: O ( 1 ) O(1) O(1)。(新元素插到表尾,不需要移动元素)最坏情况: O ( n ) O(n) O(n)。(新元素插到表头,需要将原有的n个元素全部…...
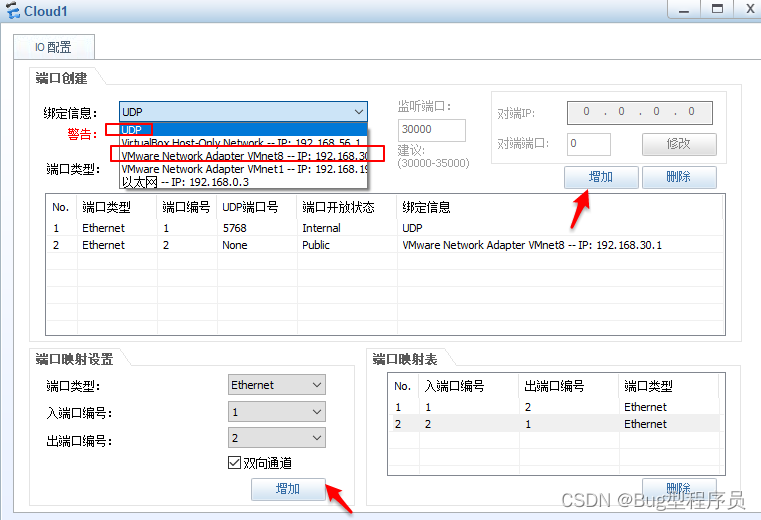
ensp与虚拟机搭建测试环境
1.虚拟机配置 ①首先确定VMnet8 IP地址,若要修改IP地址,保证在启动Ensp前操作 ②尽量保证NAT模式 2.ensp配置 (1)拓扑结构 (2)Cloud配置 ①首先点击 绑定信息 UDP → 增加 ②然后点击 绑定信息 VMware ... → 增加 ③最后在 端口映射设置上点击双向通…...

linux内核中的 指针 和 unsigned long
文章目录 1.指针的来源2.指针的定义:3.字长和数据类型4.Linux内核为什么常用unsigned long来替代指针?参考资料 1.指针的来源 方便引用一个内存地址。 给定一个内存地址,CPU就可以取出该地址的数据。 给定一个内存地址,CPU就可以…...
STM32--GPIO
文章目录 GPIO简介GPIO的基本结构GPIO位结构GPIO模式LED和蜂鸣器LED闪烁工程及程序原码代码: 蜂鸣器工程和程序原码代码 传感器光敏传感器控制蜂鸣器工程代码 GPIO简介 GPIO(General Purpose Input Output)是通用输入/输出口的简称。它是一种…...

剑指 Offer ! 61. 扑克牌中的顺子
参考资料:力扣K神的讲解 剑指 Offer 61. 扑克牌中的顺子 简单 351 相关企业 从若干副扑克牌中随机抽 5 张牌,判断是不是一个顺子,即这5张牌是不是连续的。2~10为数字本身,A为1,J为11,Q为12&…...

《玩转Python数据分析专栏》大纲
欢迎来到《玩转Python数据分析分类专栏》!在这个专栏中,我们将带您深入探索数据分析的世界,以Python为工具,解析各个领域的实际应用场景。通过100篇教程,我们将逐步引领您从入门级到高级,从基础知识到实战技巧,助您成为一名优秀的数据分析师。 专栏目标 本专栏旨在帮助…...
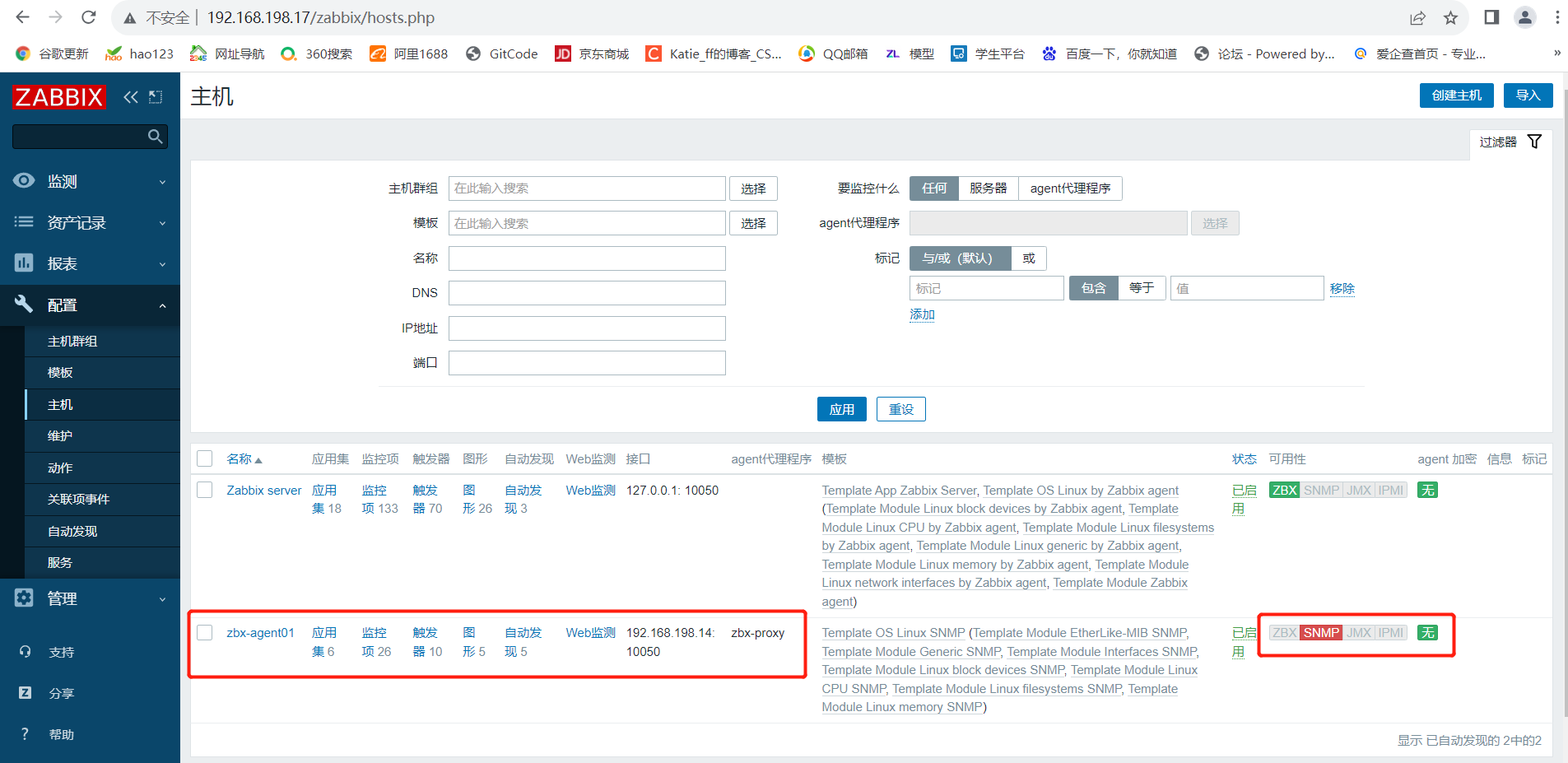
Zabbix自动注册服务器及部署代理服务器
文章目录 一.zabbix自动注册1.什么是自动注册2.环境准备3.zabbix客户端配置4.在 Web 页面配置自动注册5.验证自动注册 二.部署 zabbix 代理服务器1.分布式监控的作用:2.环境部署3.代理服务器配置4.客户端配置5.web页面配置5.1 删除原来配置5.2 添加代理5.3 创建主机…...

SpringBoot下使用自定义监听事件
事件机制是Spring的一个功能,目前我们使用了SpringBoot框架,所以记录下事件机制在SpringBoot框架下的使用,同时实现异步处理。事件机制其实就是使用了观察者模式(发布-订阅模式)。 Spring的事件机制经过如下流程: 1、自定义事件…...
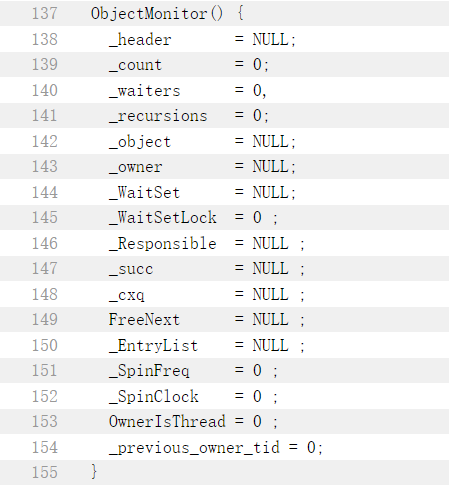
并发编程面试题1
并发编程面试题1 一、原子性高频问题: 1.1 Java中如何实现线程安全? 多线程操作共享数据出现的问题。 锁: 悲观锁:synchronized,lock乐观锁:CAS 可以根据业务情况,选择ThreadLocal,让每个…...
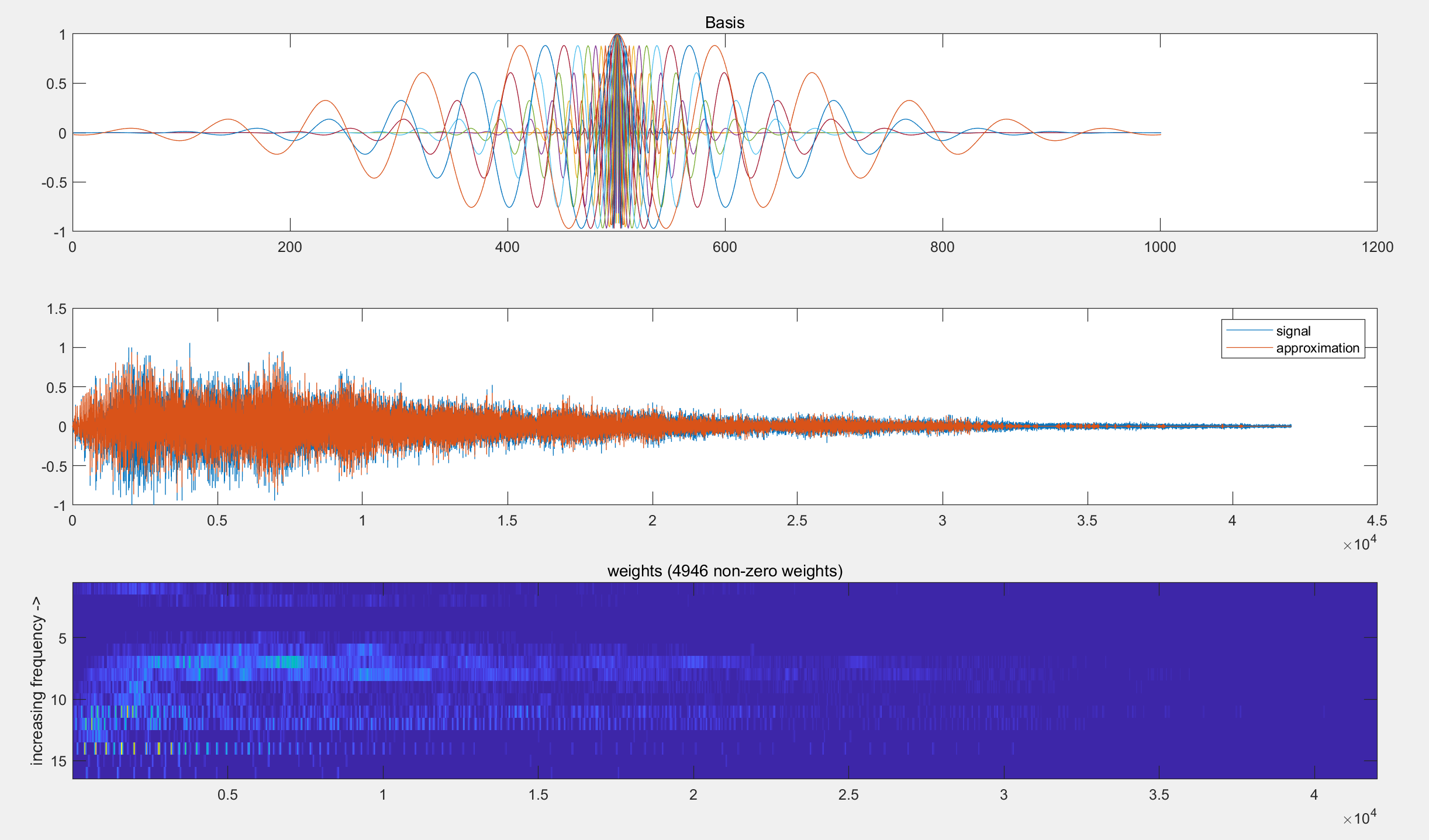
【对于一维信号的匹配】对一个一维(时间)信号y使用自定义基B执行匹配追踪(MP)研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
【Oracle 数据库 SQL 语句 】积累1
Oracle 数据库 SQL 语句 1、分组之后再合计2、显示不为空的值 1、分组之后再合计 关键字: grouping sets ((分组字段1,分组字段2),()) select sylbdm ,count(sylbmc) a…...

Django中级指南:理解并实现Django的模型和数据库迁移
Django 是一个极其强大的 Python Web 框架,它提供了许多工具和特性,能够帮助我们更快速、更便捷地构建 Web 应用。在本文中,我们将会关注 Django 中的模型(Models)和数据库迁移(Database Migrations&#x…...

Chatgpt API调用报错:openai.error.RateLimitError
Chatgpt API 调用报错: openai.error.RateLimitError: You exceeded your current quota, please check your plan and billing details. 调用OpenAI API接口 import openai import osopenai.api_key os.getenv("OPENAI_API_KEY")result openai.Chat…...

一键获取数百张免费商用人脸!AI人脸生成器来袭
随着科技的发展,人工智能正在渗透到生活的各个角落,设计行业也不例外。在网页、APP、PPT 等界面设计中,设计师经常需要插入真实的人脸素材,以增强作品的真实感和场景化。但是获取素材既不容易,质量和价格也难免成为设计…...

跳跃游戏 II——力扣45
文章目录 题目描述解法一 贪心题目描述 解法一 贪心 int jump(vector<int>& nums){in...

Stable Diffusion - 常用的负向提示 Embeddings 解析与 坐姿 (Sitting) 提示词
欢迎关注我的CSDN:https://spike.blog.csdn.net/ 本文地址:https://spike.blog.csdn.net/article/details/132145248 负向 Embeddings 是用于提高 StableDiffusion 生成图像质量的技术,可以避免生成一些不符合预期的图像特征,比如…...
:C#实现指南)
工厂方法模式(一):C#实现指南
工厂方法模式是一种创建型设计模式,用于处理对象的创建问题。通过使用工厂方法模式,我们可以将对象的创建过程与使用过程分离,从而增加代码的灵活性和可维护性。 工厂方法模式的定义 工厂方法模式定义了一个创建对象的接口,但由子…...

Spring接口InitializingBean的作用和使用介绍
在Spring框架中,InitializingBean接口是一个回调接口,用于在Spring容器实例化Bean并设置Bean的属性之后,执行一些自定义的初始化逻辑。实现InitializingBean接口的Bean可以在初始化阶段进行一些必要的操作,比如数据的初始化、资源…...
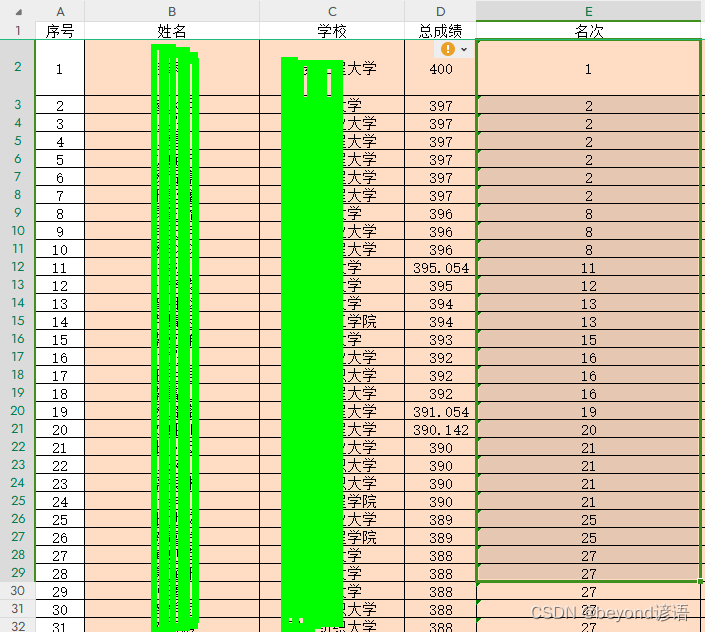
Excel---成绩相同者,名次并列排列,三步搞定
需求:一张成绩表,共341行(340条数据,第一条为标题),根据成绩进行排序,成绩相同进行名次并列 一、选择生成结果的位置,我这里点击了一下E2单元格 二、公式—>插入–>rank函数 数值:D2 表示…...

Elasticsearch6.x和7.x的区别
Elasticsearch6.x和7.x的区别 1、查找方面的区别 在增删改方面,6.x和7.x是一样的,在查找方面(分为普通查找和有高亮的查找),6.x和7.x有区别。 在7.x的es中: org.springframework.data.elasticsearch.cor…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...

算法打卡第18天
从中序与后序遍历序列构造二叉树 (力扣106题) 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,7…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...
