zookeeper增加IP白名单-安全设置
简介: zookeeper未授权访问漏洞,处理这个漏洞最简单,常用的应该就是给zookeeper添加用户名、密码验证,如果项目比较急,且代码不支持zookeeper的用户名、密码验证,那采用ip白名单过滤,无疑是最快、最有效的方法之一。
要求:zookeeper版本要求3.5以上白名单才支持设置ip地址段
注:
ZK的节点有5种操作权限:
CREATE、READ、WRITE、DELETE、ADMIN 也就是 增、删、改、查、管理权限,这5种权限简写为crwda
一、 zookeeper设置ip白名单
1、进入zk的安装目录
输入命令: cat /conf/zoo.conf查看zk的clientPort端口
2、进入zkCli
输入命令:./bin/zkCli.sh -server [address]:[client_port]例如:./bin/zkCli.sh -server [127.0.0.1]:[2181]
3、查看zk当前访问权限
输入命令:getAcl /输出:‘’World,”anyone:cdrwa //表示所有用户都有权限
4、设置白名单ip网络段(zk版本要求3.5以上,一定要将127.0.0.1添加到ip白名单过滤)
setAcl / ip:[ipaddress]:cdrwa,ip:127.0.0.1:cdrwa例如:setAcl / ip:*.*.*.224/27:cdrwa,ip:127.0.0.1:cdrwa
5、查看设置是否成功 getAcl /
输出:ip:*.*.*.224/27:cdrwa,ip:127.0.0.1:cdrwa
6、如果要恢复所有ip皆可访问,则执行
setAcl / world:anyone:cdrwa
友情链接:
zookeeper未授权访问漏洞通过添加ip白名单处理_He Yanbo的博客-CSDN博客
zookeeper增加IP白名单-安全设置_zk白名单_Gogo点的博客-CSDN博客
相关文章:

zookeeper增加IP白名单-安全设置
简介: zookeeper未授权访问漏洞,处理这个漏洞最简单,常用的应该就是给zookeeper添加用户名、密码验证,如果项目比较急,且代码不支持zookeeper的用户名、密码验证,那采用ip白名单过滤,无疑是最快…...

Mac 调试 ios safar
1. 打开Mac的 Safari 浏览器的“开发”菜单 运行 Safari 浏览器,然后依次选取“Safari 浏览器”>“偏好设置”,点按“高级”面板,然后勾选“在菜单栏中显示开发菜单”。 2. 开启IPhone的Safari调试模式 启用 Web 检查 功能,打…...
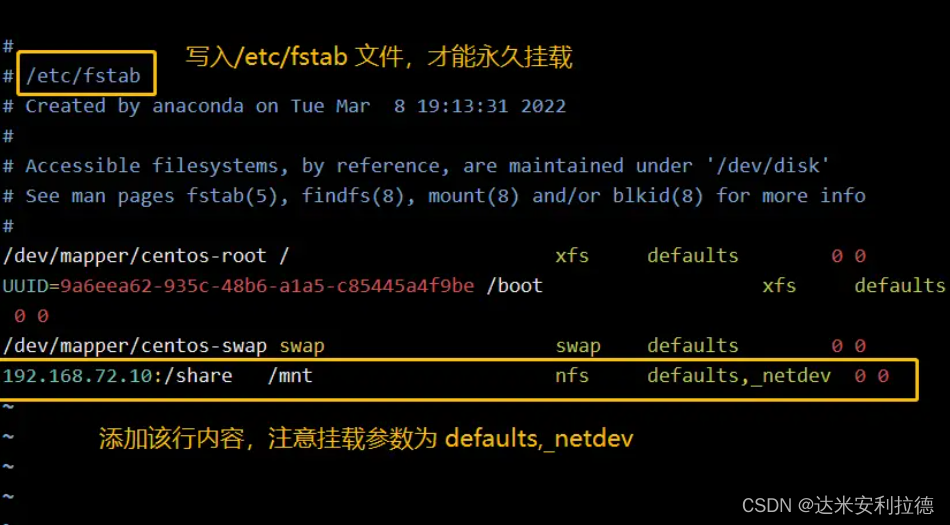
Linu网络服务NFS
linux网络服务NFS 一.NFS简介二.NFS原理三.NFS优势四.配置文件五.NFS共享存储服务的操作步骤 一.NFS简介 NFS(网络文件服务) NFS是一种基于tcp/ip传输的网络文件系统协议,最初由sun公司开放通过使用NFS协议,客户机可以像访问本地…...

24届近5年同济大学自动化考研院校分析
今天给大家带来的是同济大学控制考研分析 满满干货~还不快快点赞收藏 一、同济大学 学校简介 同济大学历史悠久、声誉卓著,是中国最早的国立大学之一,是教育部直属并与上海市共建的全国重点大学。经过115年的发展,同济大学已经…...
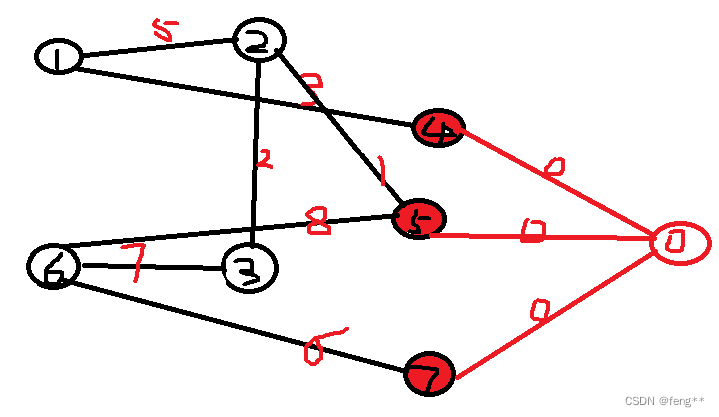
多源BFS
多源 超级源点和汇点最短距离[超级汇点]昂贵的聘礼 多源BFS矩阵距离 超级源点和汇点 超级源点跟超级汇点是模拟出来的虚拟点,多用于图中: <1>同时有多个汇点和一个源点,建立超级汇点 1、2、3、6分别到达4或者5或者7的最短路径…...
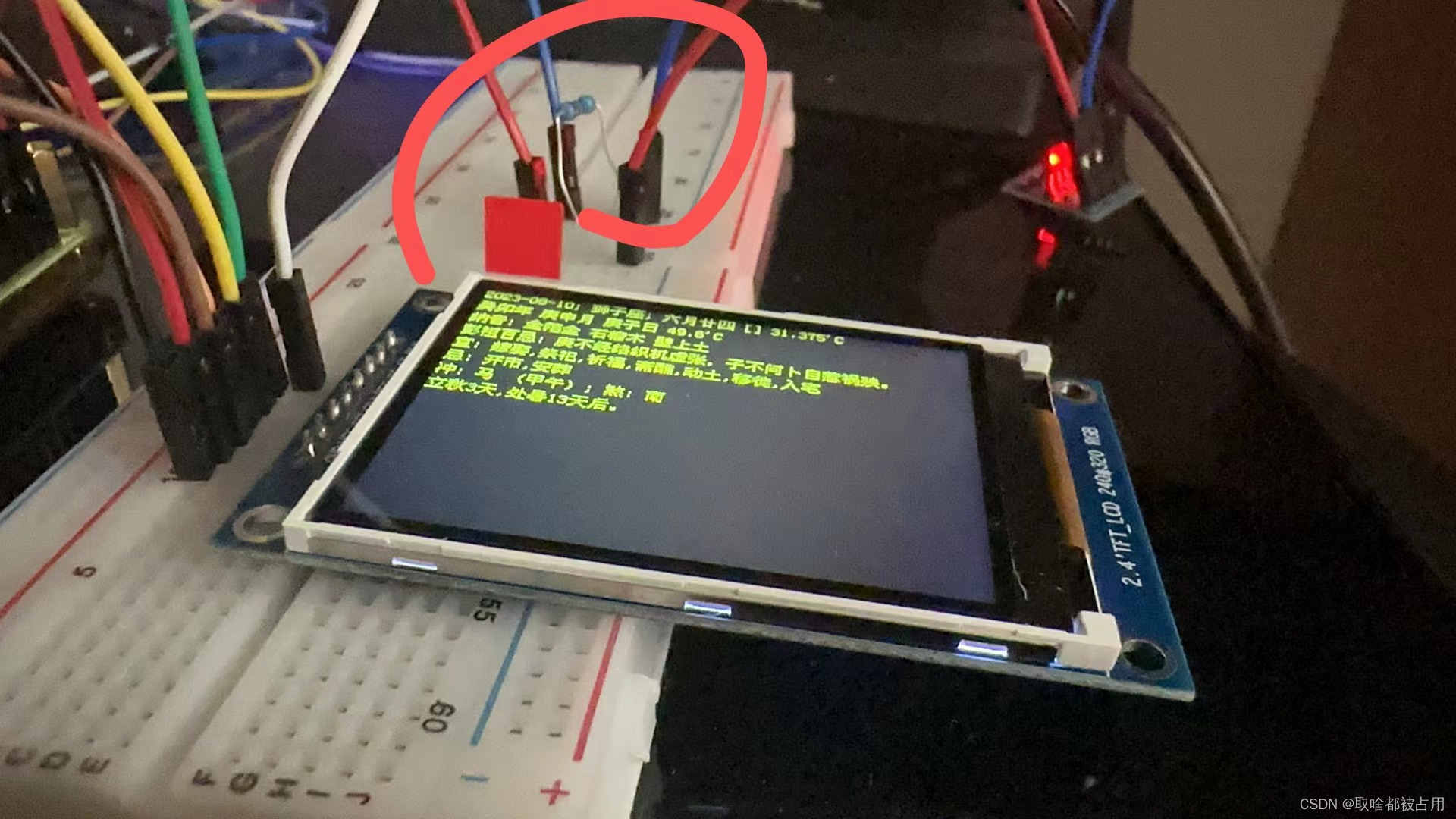
自制电子农历
水文大师上线。今天一水电子农历牌。 首先讲讲电子配件,一来是电子小屏幕的选择,遇到文字比较多的,尤其是汉字,不要选传统那款128x64 oled,绝对放不下(找到最牛的超小免费字体至少要在8pixel以上才能看清楚)。我选了i…...
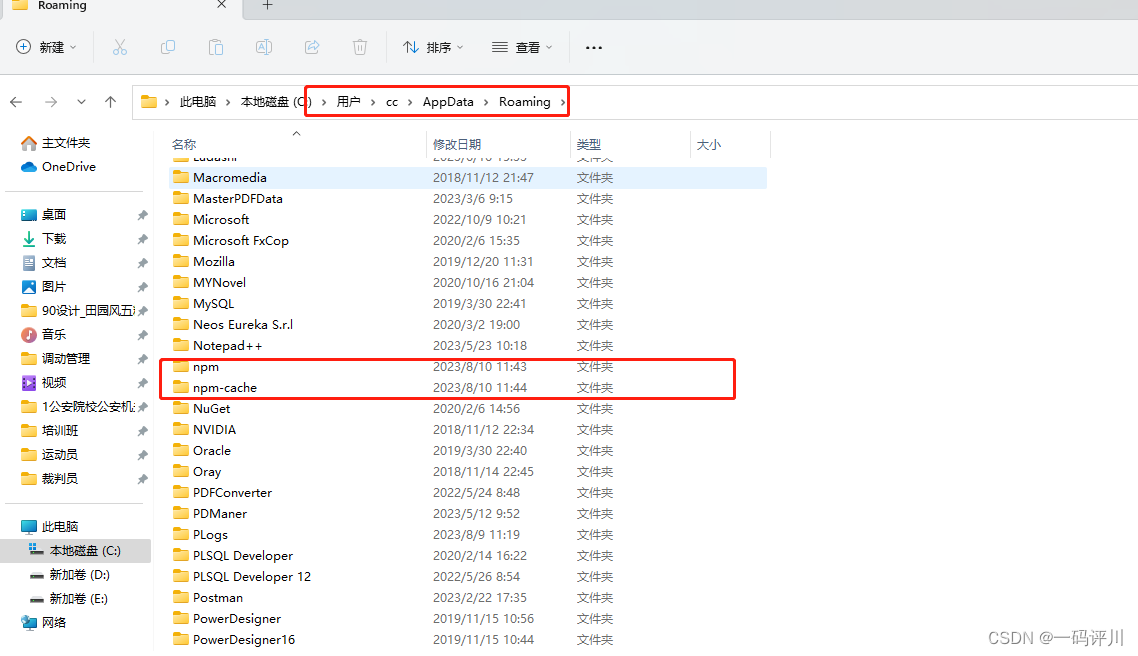
解决nvm安装后,node生效但npm无效
问题描述 nvm安装后,node生效但npm无效 清除缓存 C:\Users\cc\AppData\Roaming cc是我的用户名改成你自己的就行删除 npm和npm-cache...
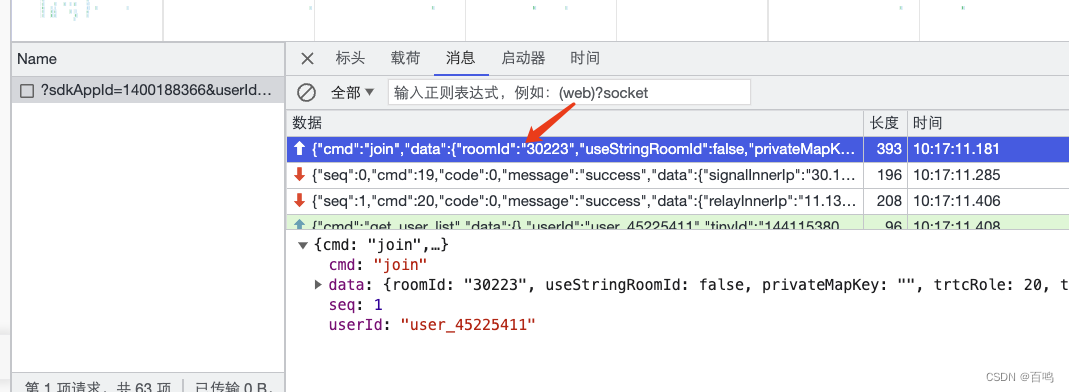
Chrome DevTools 与 WebSocket 数据查看失焦的问题
Chrome DevTools 在与 WebSocket 连接交互时可能会出现失焦的问题,这似乎是一个已知的 bug。当 DevTools 选中 WebSocket 消息时,如果有新的消息到达,DevTools 将会自动失焦,导致无法查看完整的消息内容。 虽然这个问题很令人困扰…...

Javascript 正则
基本语法 定义 JavaScript种正则表达式有两种定义方式 构造函数 var regnew RegExp(<%[^%>]%>,g);字面量 var reg/<%[^%>]%>/g;g: global,全文搜索,默认搜索到第一个结果接停止i:ingore case,忽略…...

C语言可变数组 嵌套的可变数组,翻过了山跨过了河 又掉进了坑
可变数组 专栏内容: postgresql内核源码分析 手写数据库toadb 并发编程 个人主页:我的主页 座右铭:天行健,君子以自强不息;地势坤,君子以厚德载物. 概述 数组中元素是顺序存放,这一特性让我们…...
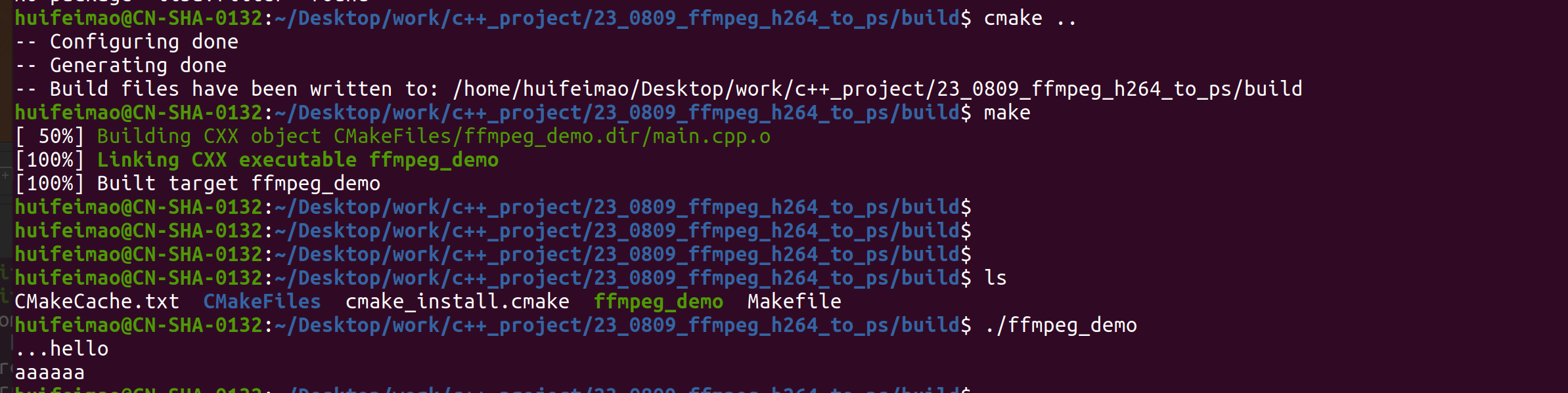
FFmpeg安装和使用
sudo apt install ffmpeg sudo apt-get install libavfilter-devcmakelist模板 CMakeLists.txt cmake_minimum_required(VERSION 3.16) project(ffmpeg_demo)# 设置ffmpeg依赖库及头文件所在目录,并存进指定变量 set(ffmpeg_libs_DIR /usr/lib/x86_64-linux-gnu) …...

HTTP代理编程:Python实用技巧与代码实例
今天我要与大家分享一些关于HTTP代理编程的实用技巧和Python代码实例。作为一名HTTP代理产品供应商,希望通过这篇文章,帮助你们掌握一些高效且实用的编程技巧,提高开发和使用HTTP代理产品的能力。 一、使用Python的requests库发送HTTP请求&a…...
)
java调用第三方接口工具类 (HttpClientUtils.java)
1. 依赖 <!--httpclient--> <dependency><groupId>commons-httpclient</groupId><artifactId>commons-httpclient</artifactId><version>3.1</version> </dependency><!-- 阿里JSON解析器 --> <dependency>…...
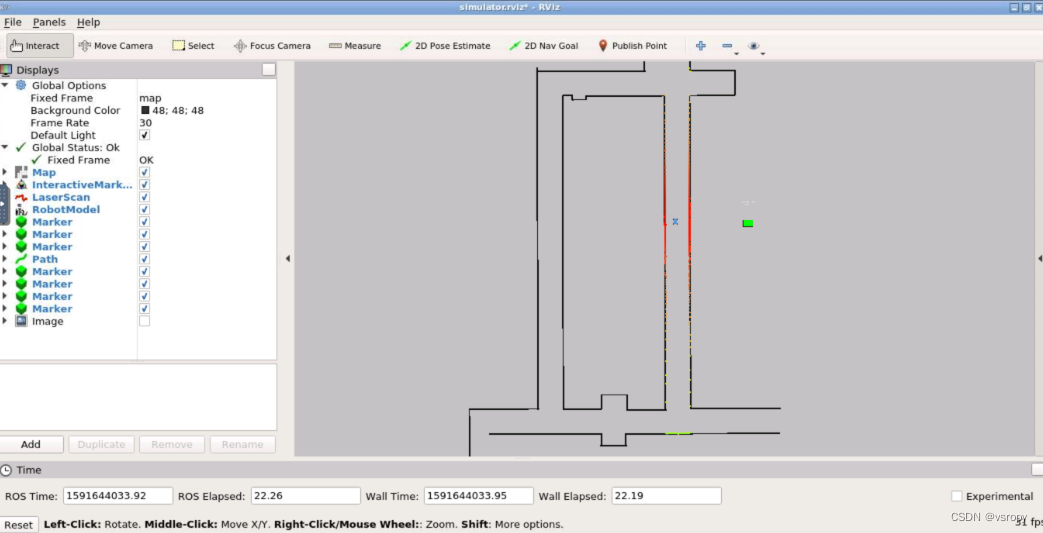
f1tenth仿真设置
文章目录 一、安装依赖二、进入工作空间克隆三、编译四、运行 一、安装依赖 tf2_geometry_msgs ackermann_msgs joy map_server sudo apt-get install ros-noetic-tf2-geometry-msgs ros-noetic-ackermann-msgs ros-melodic-joy ros-noetic-map-server 二、进入工作空间克隆…...

Technical debt (技术负债 / 技术债)
Technical debt (技术负债 / 技术债) In software development, or any other IT field (e.g., Infrastructure, Networking, etc.) technical debt (also known as design debt or code debt) is the implied cost of future reworking required when choosing an easy but li…...
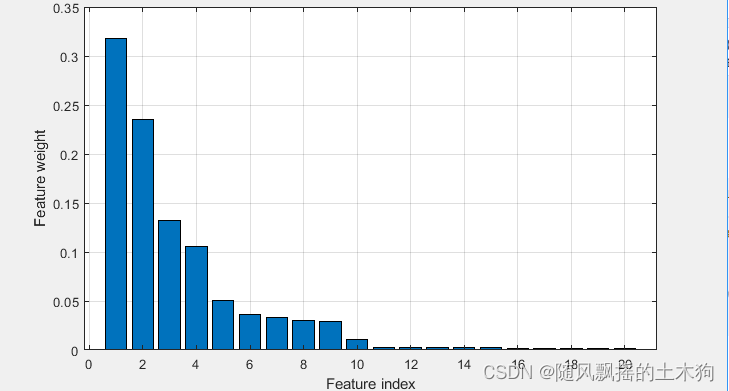
【MATLAB第67期】# 源码分享 | 基于MATLAB的morris全局敏感性分析
【MATLAB第67期】# 源码分享 | 基于MATLAB的morris全局敏感性分析 一、代码展示 clear all npoint100;%在分位数超空间中要采样的点数(计算次数iternpoint*(nfac1) nfac20;%研究函数的不确定因素数量 [mu, order] morris_sa1((x)test_function(x), nfac, npoint)for t1:size…...
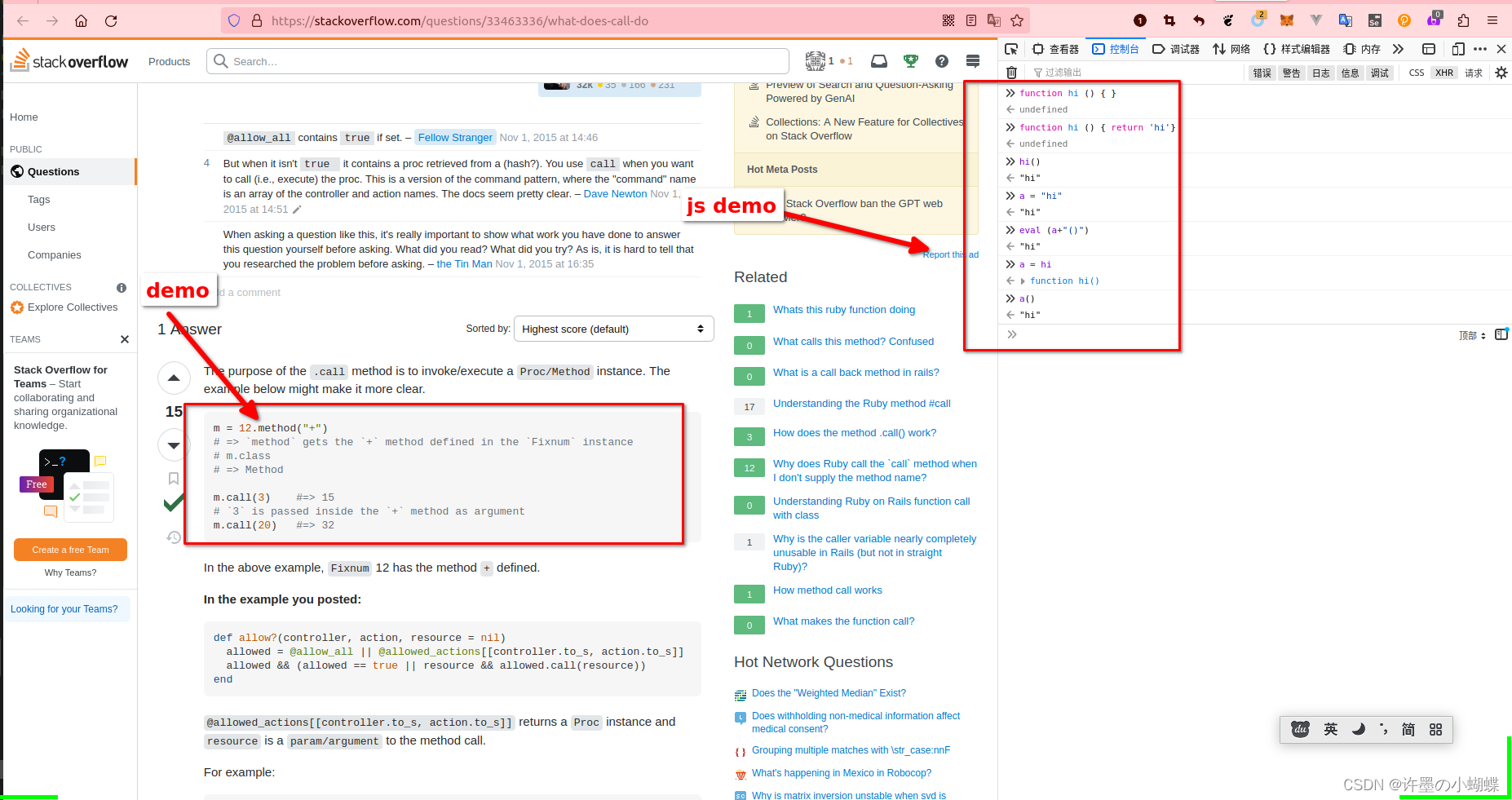
ruby send call 的简单使用
refer: ruby on rails - What does .call do? - Stack Overflow Ruby使用call 可以调用方法或者proc m 12.method("") # > method gets the method defined in the Fixnum instance # m.class # > Methodm.call(3) #> 15 # 3 is passed inside the…...

24聊城大学823软件工程考研
1.软件发展有几个阶段?各有何特征? ①程序设计阶段 硬件特征:价格贵、存储容量小、运行可靠性差。 软件特征:只有程序、程序设计概念,不重视程序设计方法。 ②程序系统阶段。 硬件特征:速度、容量及工作可…...
勘探开发人工智能技术:机器学习(3)
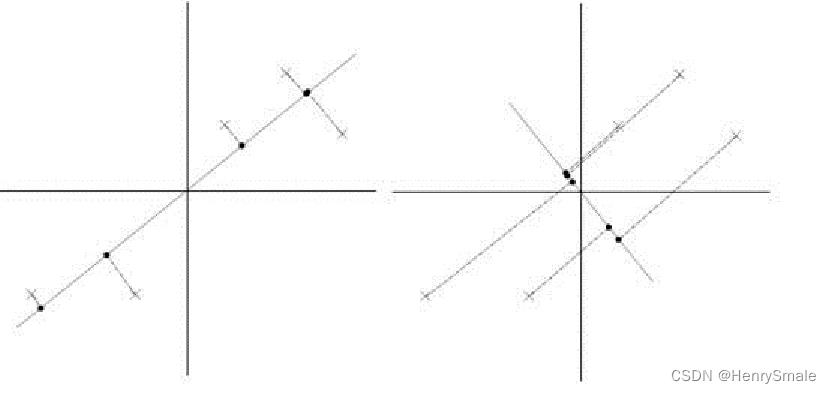
0 提纲 4.1 logistic回归 4.2 支持向量机(SVM) 4.3 PCA 1 logistic回归 用超平面分割正负样本, 考虑所有样本导致的损失. 1.1 线性分类器 logistic 回归是使用超平面将空间分开, 一边是正样本, 另一边是负样本. 因此, 它是一个线性分类器. 如图所示, 若干样本由两个特征描…...

定制 ChatGPT 以满足您的需求 自定义说明
推荐:使用 NSDT场景编辑器 快速助你搭建可二次编辑的3D应用场景 20 月 <> 日,OpenAI 宣布他们正在引入带有自定义说明的新流程,以根据您的特定需求定制 ChatGPT。 什么是自定义说明? 新的测试版自定义指令功能旨在通过防止…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

面试高频问题
文章目录 🚀 消息队列核心技术揭秘:从入门到秒杀面试官1️⃣ Kafka为何能"吞云吐雾"?性能背后的秘密1.1 顺序写入与零拷贝:性能的双引擎1.2 分区并行:数据的"八车道高速公路"1.3 页缓存与批量处理…...

2.3 物理层设备
在这个视频中,我们要学习工作在物理层的两种网络设备,分别是中继器和集线器。首先来看中继器。在计算机网络中两个节点之间,需要通过物理传输媒体或者说物理传输介质进行连接。像同轴电缆、双绞线就是典型的传输介质,假设A节点要给…...

TJCTF 2025
还以为是天津的。这个比较容易,虽然绕了点弯,可还是把CP AK了,不过我会的别人也会,还是没啥名次。记录一下吧。 Crypto bacon-bits with open(flag.txt) as f: flag f.read().strip() with open(text.txt) as t: text t.read…...
