当前位置： 首页 > news >正文

HTML ＜select＞ 标签

news 2026/2/8 17:51:11

实例

创建带有 4 个选项的选择列表：

<select><option value ="volvo">Volvo</option><option value ="saab">Saab</option><option value="opel">Opel</option><option value="audi">Audi</option>
</select>

定义和用法

select 元素可创建单选或多选菜单。

<select> 元素中的 "><option> 标签用于定义列表中的可用选项。

浏览器支持

元素ChromeIEFirefoxSafariOpera
<select>YesYesYesYesYes

所有主流浏览器都支持 <select> 标签。

HTML 4.01 与 HTML 5 之间的差异

HTML5 添加了一些新属性。

提示和注释：

提示：select 元素是一种表单控件，可用于在表单中接受用户输入。

属性

New: HTML5 中的新属性。

<
属性值描述

相关文章：

HTML ＜select＞ 标签

实例 创建带有 4 个选项的选择列表： <select><option value ="volvo">Volvo</option><option value ="saab">Saab</option><option value="opel">Opel</option><option value="audi"…...

编程日记 2023/8/11 23:02:54

Flutter：文件上传与下载（下载后预览）

Dio dio是一个强大的Dart Http请求库&#xff0c;提供了丰富的功能和易于使用的API&#xff0c;支持文件上传和下载。 这个就不介绍了&#xff0c;网上有很多的封装案例。 background_downloader 简介 适用于iOS&#xff0c;Android&#xff0c;MacOS&#xff0c;Windows和L…...

编程日记 2023/8/11 23:01:50

[前端系列第6弹]Ajax简明教程：轻松实现Web页面的异步交互

在这篇文章中&#xff0c;我将介绍Ajax的基本概念、原理、优缺点、实现方法和应用场景&#xff0c;以及如何使用它来实现Web页面的异步交互。还将给一些简单而实用的例子&#xff0c;让你可以跟着我一步一步地编写自己的Ajax代码。 目录 一、什么是Ajax 二、如何使用Ajax &a…...

编程日记 2023/8/11 23:00:49

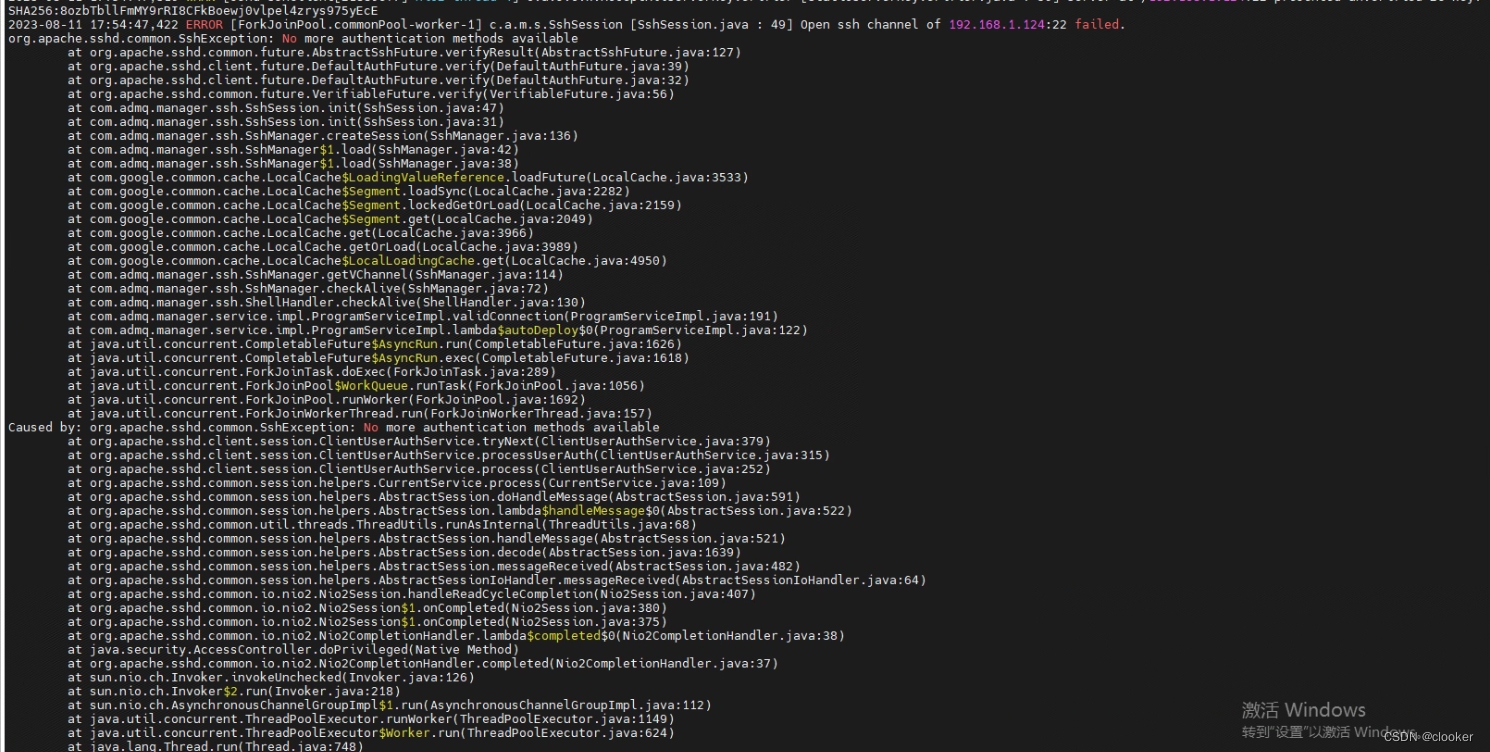
ssh-keygen 做好免密登录后不生效

免密说明 通常情况下&#xff0c;我们ssh到其他服务器需要知道服务器的用户名和密码。对于需要经常登录的服务器每次都输入密码比较麻烦&#xff0c;因此我们可以在两台服务器上做免密登录&#xff0c;即在A服务器可以免密登录B服务器。 在A服务器上登录B服务器时&#xff0c;…...

编程日记 2023/8/11 22:59:48

【Java可执行命令】（十八）可视化监控和管理工具 jconsole：获取 JVM的内存使用情况、线程活动、GC 行为等重要指标的可视化工具 ~

Java可执行命令之jconsole 1️⃣ 概念2️⃣ 优势和缺点3️⃣ 使用3.1 语法格式3.2 注意事项 4️⃣ 应用场景&#x1f33e; 总结 1️⃣ 概念 jconsole 是 Java Development Kit (JDK) 自带的一款图形化监控和管理工具。它旨在提供一个简单而强大的界面&#xff0c;用于监视和管…...

编程日记 2023/8/11 22:58:47

leetcode做题笔记66

给定一个由 整数 组成的 非空 数组所表示的非负整数&#xff0c;在该数的基础上加一。 最高位数字存放在数组的首位&#xff0c; 数组中每个元素只存储单个数字。 你可以假设除了整数 0 之外&#xff0c;这个整数不会以零开头。 思路一&#xff1a;模拟题意 int* plusOne(i…...

编程日记 2023/8/11 22:57:44

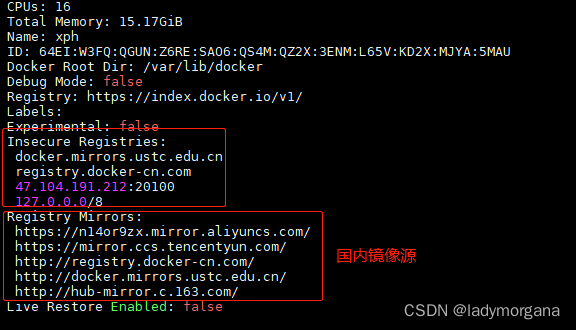
【docker】设置 docker 国内镜像报错，解决方案

一、报错&#xff1a; [rootlocalhost ~]# systemctl restart docker Job for docker.service failed because the control process exited with error code. See "systemctl status docker.service" and "journalctl -xe" for details.二、原因&#xf…...

编程日记 2023/8/11 22:56:43

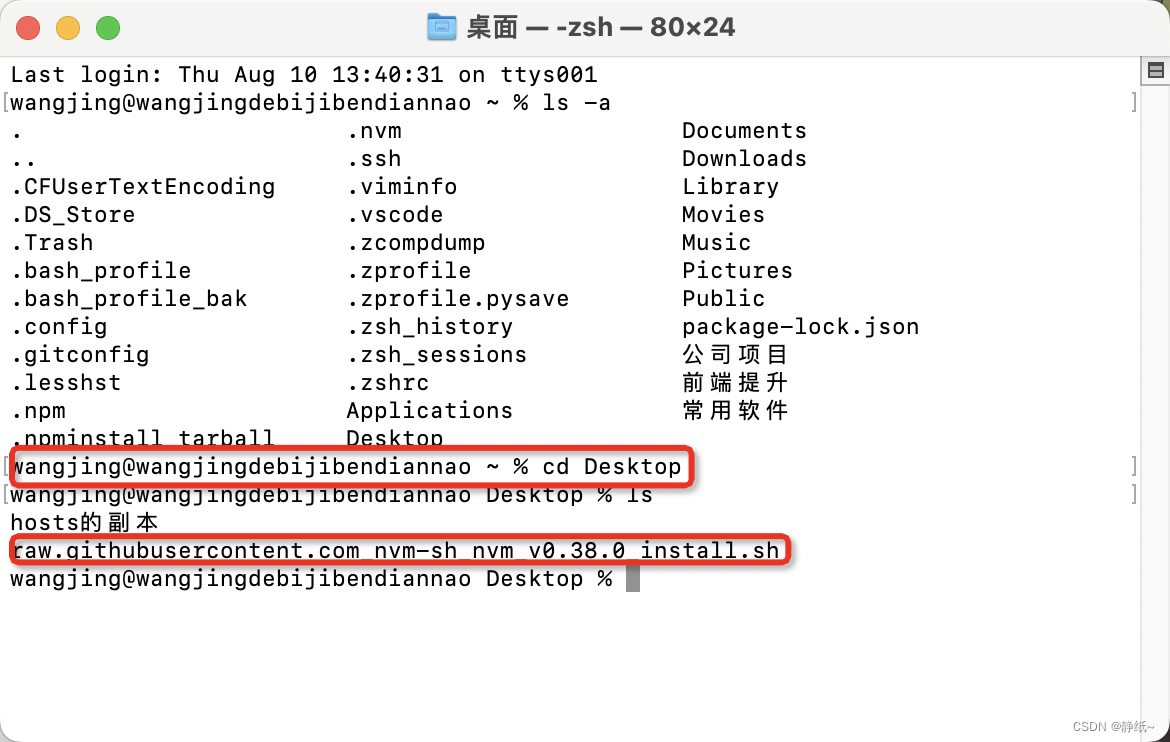
mac安装nvm管理工具遇到的问题和解决方法

nvm 是一款可以管理多版本node的工具&#xff0c;因为是刚买没多久的电脑之前用的都是windows&#xff0c;昨天折腾了一下午终于倒腾好了 第一步&#xff1a; 卸载电脑已有的node&#xff1b;访问nvm脚本网址&#xff0c;另存为到电脑上任何目录&#xff0c;我是放在桌面上的…...

编程日记 2023/8/11 22:55:42

DocX 生成Word

当然&#xff0c;这里是一个使用DocX库在.NET Core中操作Word文档的简单示例&#xff1a; 首先&#xff0c;确保你在项目中安装了DocX库。你可以在NuGet包管理器中搜索并安装DocX。 然后&#xff0c;使用以下代码来创建一个简单的Word文档并添加一些内容&#xff1a; using …...

编程日记 2023/8/11 22:54:37

数据库新闻速递 -- POSTGRESQL 正在蚕食数据库市场 （翻译）

开头还是介绍一下群&#xff0c;如果感兴趣polardb ,mongodb ,mysql ,postgresql ,redis 等有问题&#xff0c;有需求都可以加群群内有各大数据库行业大咖&#xff0c;CTO&#xff0c;可以解决你的问题。加群请加 liuaustin3微信号 &#xff0c;在新加的朋友会分到3群&#xff…...

编程日记 2023/8/11 22:53:34

PAT 1085 Perfect Sequence

个人学习记录&#xff0c;代码难免不尽人意 Sample Input: 10 8 2 3 20 4 5 1 6 7 8 9 Sample Output: 8 #include<cstdio> #include<iostream> #include<vector> #include<algorithm> #include<string> #include<map> #include<cmath&…...

编程日记 2023/8/11 22:52:32

软件测试面试夺命连环十七问，你答得上来么？这都不会建议多学！

1. 给你一个网站&#xff0c;该如何测试&#xff1f;&#xff08;探究需求制订计划&#xff09; 首先&#xff0c;查找需求说明、网站设计等相关文档&#xff0c;分析测试需求。 制定测试计划&#xff0c;确定测试范围和测试策略&#xff0c;一般包括以下几个部分&#xff1a…...

编程日记 2023/8/11 22:51:30

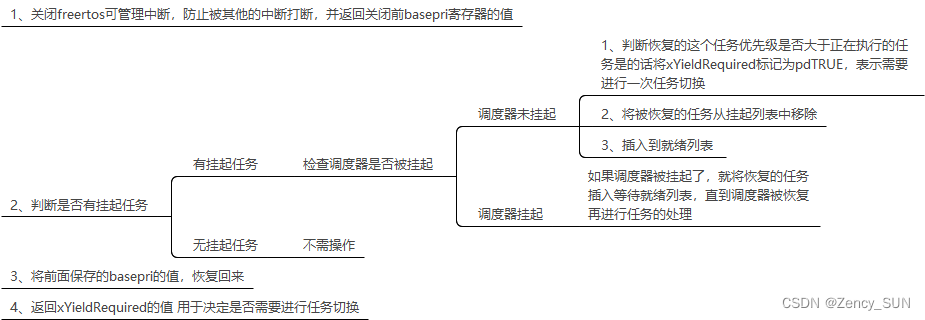
【学习FreeRTOS】第5章——FreeRTOS任务挂起与恢复

1.任务的挂起与恢复的API函数 vTaskSuspend() ——挂起任务&#xff08;类似暂停&#xff0c;可恢复&#xff0c;但删除任务&#xff0c;无法恢复&#xff09;vTaskResume() ——恢复被挂起的任务xTaskResumeFromISR()—— 在中断中恢复被挂起的任务 1.1.任务挂起函数vTaskSu…...

编程日记 2023/8/11 22:50:29

gitblit-使用

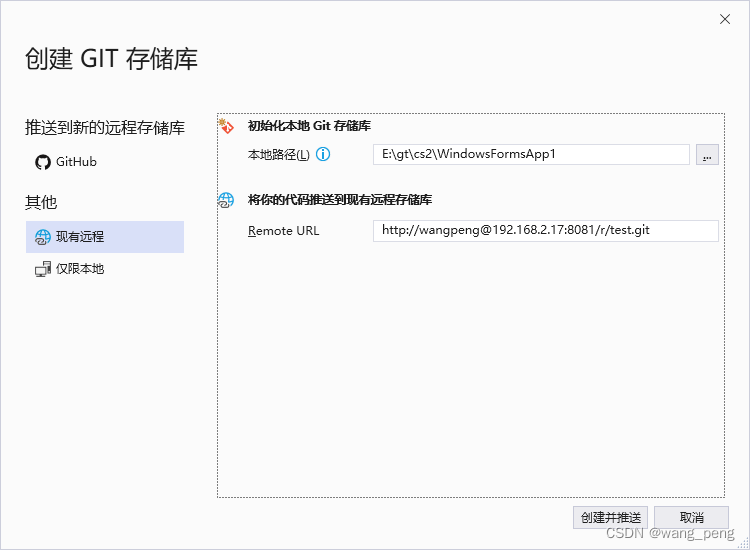
1.登入GitBlit服务器 默认用户和密码: admin/admin 2.创建一个新的版本库 点击图中的“版本库”&#xff0c;然后点击图中“创建版本库” 填写名称和描述&#xff0c;注意名称最后一定要加 .git选择限制查看、克隆和推送勾选“加入README”和“加入.gitignore文件”在图中的1处…...

编程日记 2023/8/11 22:49:28

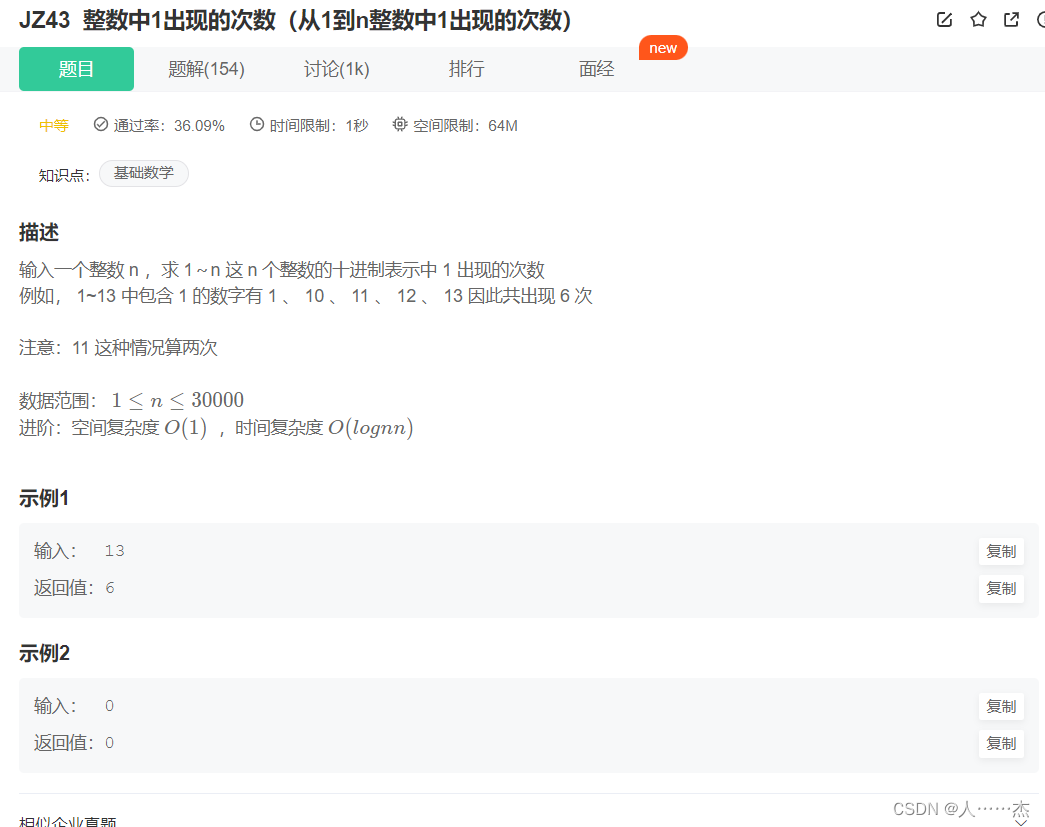
整数中1出现的次数(从1到n整数中1出现的次数)

解题思路1&#xff1a; 设定整数点&#xff08;如1、10、100等等&#xff09;作为位置点i&#xff08;对应n的各位、十位、百位等等&#xff09;&#xff0c;分别对每个数位上有多少包含1的点进行分析。 第一步&#xff1a;对n进行分割&#xff0c;分为两部分&#xff1a;高位…...

编程日记 2023/8/11 22:48:26

Vue2：路由

Vue2&#xff1a;路由 Date: May 28, 2023 Sum: vue-router基本使用、高级用法 单页面应用程序 概念&#xff1a;SPA【Single Page Application】是指所有的功能都在一个html页面上实现 案例&#xff1a; 单页应用网站&#xff1a; 网易云音乐 https://music.163.com/ 多页…...

编程日记 2023/8/11 22:47:26

【Docker】Docker的应用场景，Docker 的优点，Ubuntu Docker 安装，使用 Shell 脚本进行安装

作者简介&#xff1a; 辭七七&#xff0c;目前大一&#xff0c;正在学习C/C&#xff0c;Java&#xff0c;Python等 作者主页&#xff1a; 七七的个人主页 文章收录专栏&#xff1a; 七七的闲谈 欢迎大家点赞 &#x1f44d; 收藏 ⭐ 加关注哦&#xff01;&#x1f496;&#x1f…...

编程日记 2023/8/11 22:46:25

CentOS7 启动谷歌浏览器 java+Selenium+chrome+chromedriver

前言&#xff1a;自己想使用该技术实现自动化抓取音乐&#xff0c;目前在window上运行成功&#xff0c;需要在Linux Centos服务上跑&#xff0c;配置上出现了许多问题&#xff0c;特此记录。 参考文档&#xff1a;CentOS7 安装Seleniumchromechromedriverjava_远方丿的博客-CSD…...

编程日记 2023/8/11 22:45:24

【无公网IP】在公网环境下Windows远程桌面Ubuntu 18.04

【无公网IP】在公网环境下Windows远程桌面Ubuntu 18.04 文章目录 *【无*公网IP】在公网环境下Windows远程桌面Ubuntu 18.04一、 同个局域网内远程桌面Ubuntu1. 更新软件仓库2. 安装支持包3. 安装XFCE4桌面环境4. 安装XRDP5. 环境设置5.1 XFCE桌面配置5.2 在配置文件中&#xff…...

编程日记 2023/8/11 22:44:22

Java“牵手拼多多商品详情数据采集方法，拼多多API接口申请指南

拼多多详情接口 API 是开放平台提供的一种 API 接口&#xff0c;它可以帮助开发者获取商品的详细信息&#xff0c;包括商品的标题、描述、图片等信息。在电商平台的开发中&#xff0c;详情接口API是非常常用的 API&#xff0c;因此本文将详细介绍详情接口 API 的使用。 一、拼…...

编程日记 2023/8/11 22:43:22

rknn优化教程（二）

文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK&#xff0c;开始写第二篇的内容了。这篇博客主要能写一下&#xff1a; 如何给一些三方库按照xmake方式进行封装&#xff0c;供调用如何按…...

编程新知 2025/6/11 15:25:30

UE5 学习系列（三）创建和移动物体

这篇博客是该系列的第三篇&#xff0c;是在之前两篇博客的基础上展开&#xff0c;主要介绍如何在操作界面中创建和拖动物体&#xff0c;这篇博客跟随的视频链接如下&#xff1a; B 站视频&#xff1a;s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

编程新知 2026/1/24 10:00:31

Java多线程实现之Callable接口深度解析

Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

编程新知 2026/1/25 6:36:06

IT供电系统绝缘监测及故障定位解决方案

随着新能源的快速发展&#xff0c;光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域&#xff0c;IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选&#xff0c;但在长期运行中&#xff0c;例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

编程新知 2026/2/1 6:36:36

全志A40i android7.1 调试信息打印串口由uart0改为uart3

一&#xff0c;概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本&#xff1a;2014.07&#xff1b; Kernel版本&#xff1a;Linux-3.10&#xff1b; 二&#xff0c;Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01)&#xff0c;并让boo…...

编程新知 2026/2/5 6:28:09

Git常用命令完全指南：从入门到精通

Git常用命令完全指南&#xff1a;从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

编程新知 2025/10/3 0:40:01

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程

下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...

编程新知 2025/8/18 11:32:48

Unity VR/MR开发-VR开发与传统3D开发的差异

视频讲解链接&#xff1a;【XR马斯维】VR/MR开发与传统3D开发的差异【UnityVR/MR开发教程--入门】_哔哩哔哩_bilibili...

编程新知 2026/2/5 4:00:33

机器学习的数学基础：线性模型

线性模型 线性模型的基本形式为&#xff1a; f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法&#xff0c;得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...

编程新知 2025/10/2 9:07:50

2025-05-08-deepseek本地化部署

title: 2025-05-08-deepseek 本地化部署 tags: 深度学习 程序开发 2025-05-08-deepseek 本地化部署 参考博客 本地部署 DeepSeek&#xff1a;小白也能轻松搞定&#xff01; 如何给本地部署的 DeepSeek 投喂数据&#xff0c;让他更懂你 [实验目的]&#xff1a;理解系统架构与原…...

编程新知 2026/2/4 16:20:49