(十)人工智能应用--深度学习原理与实战--模型的保存与加载使用
目的:将训练好的模型保存为文件,下次使用时直接加载即可,不必重复建模训练。
神经网络模型训练好之后,可以保存为文件以持久存储,这样下次使用时就不重新建模训练,直接加载就可以。TensorfLow提供了灵活的模型保存方案,既可以同时保存网络结构和权重(即保存全模型),也可以仅保存权重或网络结构。本章节通过案例来学习和掌握模型的多种保存方法。
学习内容:
a)全模型的保存与加载、使用
b)权重数据的保存及加载
c)网络结构的保存及加载
学习目标:
掌握全模型信息的保存与加载方法
掌握权重数据的保存及加载方法
掌握网络结构的保存及加载方法
方案一:保存全模型(网络结构+权重+编译配置)
1、搭建并训练好神经网络模型
from tensorflow.keras import datasets,layers,modelsmodel = models.Sequential() # 定义模型对象model.add(layers.Dense(512,activation = 'relu', input_shape = (28*28,))) # 输入层model.add(layers.Dense(10,activation = 'softmax')) #输出层model.summary()
输出结果:

#加载、处理数据
(X_train,y_train),(X_test&#相关文章:

(十)人工智能应用--深度学习原理与实战--模型的保存与加载使用
目的:将训练好的模型保存为文件,下次使用时直接加载即可,不必重复建模训练。 神经网络模型训练好之后,可以保存为文件以持久存储,这样下次使用时就不重新建模训练,直接加载就可以。TensorfLow提供了灵活的模型保存方案,既可以同时保存网络结构和权重(即保存全模型),也可…...

Java“牵手”1688商品详情页面数据获取方法,1688API实现批量商品数据抓取示例
背景:1688商城是一个网上购物平台,售卖各类商品,包括服装、鞋类、家居用品、美妆产品、电子产品等。要获取1688商品详情数据,您可以通过开放平台的接口或者直接访问1688商城的网页来获取商品详情信息。以下是两种常用方法的介绍&a…...

Docker_docker runContainerd
docker run-Containerd docker run -it 运行容器交互式方式启动守护进程方式启动其他命令 docker部署nginx服务k8s废弃docker原因安装和配置containerdcontainerd常用命令 docker run -it 运行容器 交互式方式启动 # 以交互式方式启动并进入容器 docker run --namehello -it …...

python中常见的矩阵变换总结
利用python做数据处理和分析过程中,如在开展机器学习的数据预处理、数据格式转换等等,不可避免的会涉及到各种矩阵变换,其中使用最多的就是numpy下的矩阵变换,以下是日常用到的一些矩阵变换总结,主要有矩阵中数据类型的…...
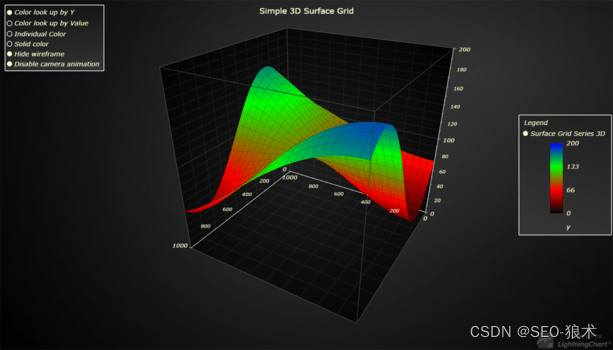
LightningChart JS 2023Crack,CPU高效实时更新
LightningChart JS 2023Crack,CPU高效实时更新 添加了新的极地热图图表类型-添加了新系列类型,允许您在极地坐标系中可视化热图。极地热图的一些关键特征是: 处理多达400万个数据点。 快速加载速度和CPU高效实时更新。 100ms以完全显示由所有数据填充的热…...
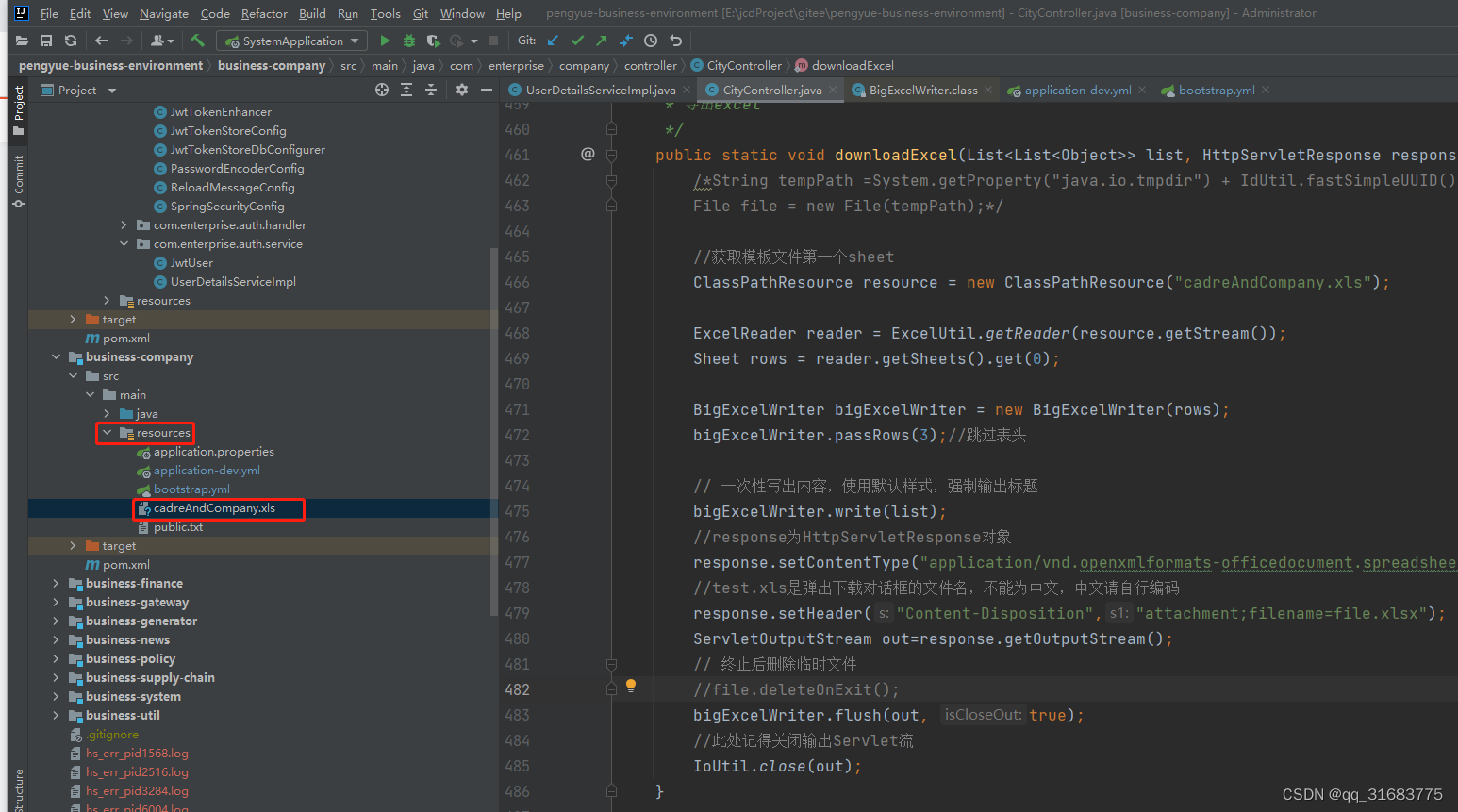
hutool 导出复杂表头excel
假如已这样的表头导出数据 1.把包含表头的excel添加到项目资源目录 2.编写代码读取表头所在sheet,并且加入需导出的数据 /*** 导出excel*/public static void downloadExcel(List<List<Object>> list, HttpServletResponse response) throws IOException {/*Strin…...
git和github学习
一、什么是git和github? 二、学会使用github desktop应用程序 初始使用: 一开始我们是新账户,里面是没有仓库的,需要手动创建一个仓库。此时,这个仓库是创建在本地仓库里面,需要用到push命令(就是那个pub…...

竞赛项目 车位识别车道线检测 - python opencv
0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 深度学习 机器视觉 车位识别车道线检测 该项目较为新颖,适合作为竞赛课题方向,学长非常推荐! 🥇学长这里给一个题目综合评分(每项满分5分) …...

中文版开源Llama 2同时有了语言、多模态大模型,完全可商用
可以说,AI 初创公司 LinkSoul.Al 的这些开源项目让海外开源大模型在国内的普及和推广速度与国际几乎保持了一致。 7 月 19 日,Meta 终于发布了免费可商用版本 Llama 2,让开源大模型领域的格局发生了巨大变化。 Llama 2 模型系列包含 70 亿、…...
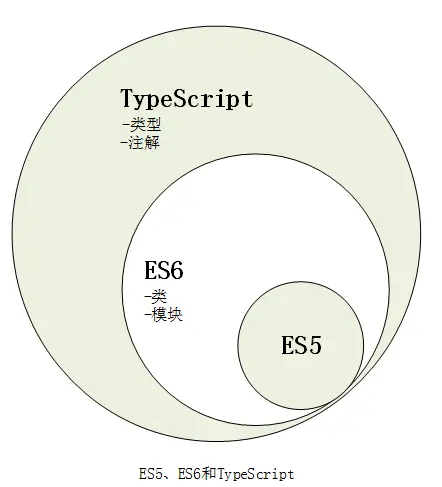
JavaScript、TypeScript、ES5、ES6之间的联系和区别
ECMAScript: 一个由 ECMA International 进行标准化,TC39 委员会进行监督的语言。通常用于指代标准本身。JavaScript: ECMAScript 标准的各种实现的最常用称呼。这个术语并不局限于某个特定版本的 ECMAScript 规范,并且可能被用于…...
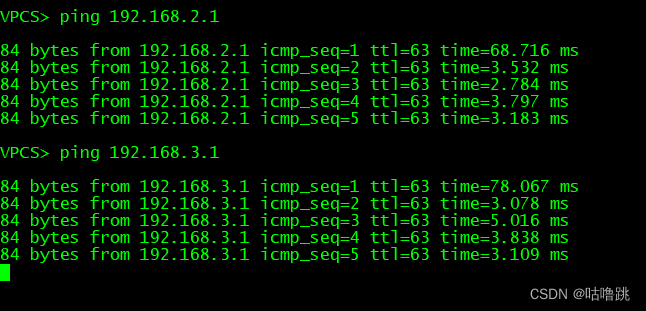
RCNA——单臂路由
一,实验背景 之前的VLAN实现的很多都是相同部门互相访问,不同部门无法访问。不过这次整来了一个路由器,领导说大部分的部门虽说有保密信息需要互相隔离,但是这些部门和其它部门也应该互相连通以方便工作交流。因此要配置新的环境&…...

leetcode做题笔记69
给你一个非负整数 x ,计算并返回 x 的 算术平方根 。 由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。 注意:不允许使用任何内置指数函数和算符,例如 pow(x, 0.5) 或者 x ** 0.5 。 思路一ÿ…...
!)
CentOS根分区扩容实战(非LVM)!
在虚拟化平台(如KVM,ESXI)中,将虚拟机的磁盘大小扩展到所需的大小。这将增加虚拟机的磁盘空间。 在虚拟机中,使用以下命令查看可用的磁盘和分区信息: sudo fdisk -l确定要扩展的根分区的设备名称(如 /dev/…...
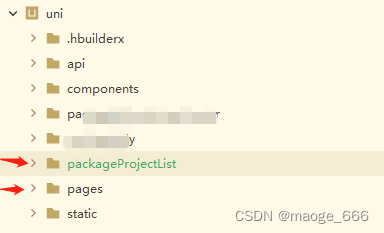
uniapp 微信小程序 分包
1、manifest.json内添加如图所示: "optimization" : {"subPackages" : true },2、在与pages同级上创建各个分包的文件夹 把需要分包的文件对应移入分包文件夹内 3、page.json内修改分包文件的路径 比如: {"path" : &qu…...

Redis_安装、启动以及基本命令
2.Redis安装 2.1前置处理环境 VMware安装安装centOS的linux操作系统xshellxftp 2.2 配置虚拟机网络 按ctrlaltf2 切换到命令行 cd (/)目录 修改/etc/sysconfig/network-scripts/ifcfg-ens3 vi 命令 按insert表示插入 按ctrlesc退出修改状态 :wq 写入并退出 此文件必须保持一…...

IPv4编址及子网划分
IPv4编址及子网划分 一、IPv4地址概述1.1、IPv4报文结构1.2、IPv4地址分类1.2.1、A类1.2.2、B类1.2.3、C类1.2.4、D类1.2.5、E类 1.3、私有IP地址1.4、特殊地址 二、子网划分2.1、子网掩码2.2、VLSM 可变长的子网掩码2.3、子网划分2.4、子网划分示例2.4.1、子网划分案例 —— A…...
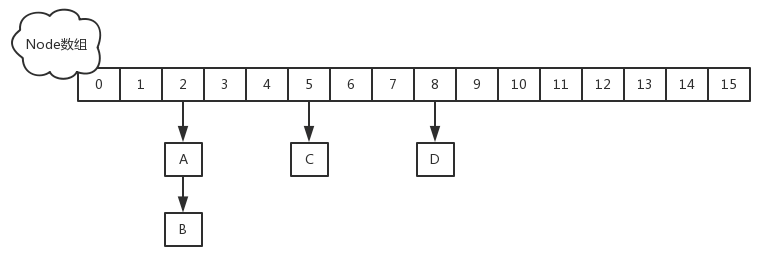
HashMap 二十一问
1:HashMap 的数据结构? A:哈希表结构(链表散列:数组链表)实现,结合数组和链表的优点。当链表长度超过 8 时,链表转换为红黑树。transient Node<K,V>[] table; 2:…...
什么是Selenium?使用Selenium进行自动化测试
什么是 Selenium? Selenium 是一种开源工具,用于在 Web 浏览器上执行自动化测试(使用任何 Web 浏览器进行 Web 应用程序测试)。 等等,先别激动,让我再次重申一下,Selenium 仅可以测试We…...

解决“先commit再pull”造成的git冲突
一、问题场景 在分支上修改了代码然后commit(没有push),此时再git pull,拉下了别人的修改,但是报错无法merge 二、解决步骤 1.在idea下方工具栏选择git -> log,可以看到版本变化链表,右键…...
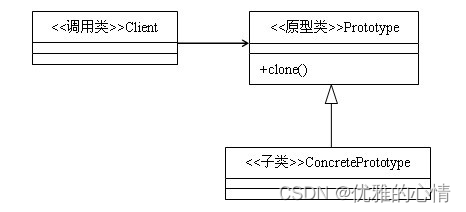
JAVA设计模式----原型设计模式
文章目录 一、简介二、实现方式三、原型模式的注意事项浅拷贝与深拷贝浅拷贝深拷贝一、简介 定义:用原型实例指定创建对象的种类,并通过拷贝这些原型创建新的对象。 类型:创建类模式 类图: 原型模式主要用于对象的复制,它的核心是就是类图中的原型类Prototype。Protot…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

【若依】框架项目部署笔记
参考【SpringBoot】【Vue】项目部署_no main manifest attribute, in springboot-0.0.1-sn-CSDN博客 多一个redis安装 准备工作: 压缩包下载:http://download.redis.io/releases 1. 上传压缩包,并进入压缩包所在目录,解压到目标…...

Linux中INADDR_ANY详解
在Linux网络编程中,INADDR_ANY 是一个特殊的IPv4地址常量(定义在 <netinet/in.h> 头文件中),用于表示绑定到所有可用网络接口的地址。它是服务器程序中的常见用法,允许套接字监听所有本地IP地址上的连接请求。 关…...

基于Python的气象数据分析及可视化研究
目录 一.🦁前言二.🦁开源代码与组件使用情况说明三.🦁核心功能1. ✅算法设计2. ✅PyEcharts库3. ✅Flask框架4. ✅爬虫5. ✅部署项目 四.🦁演示效果1. 管理员模块1.1 用户管理 2. 用户模块2.1 登录系统2.2 查看实时数据2.3 查看天…...
