【1572. 矩阵对角线元素的和】
来源:力扣(LeetCode)
描述:
给你一个正方形矩阵 mat,请你返回矩阵对角线元素的和。
请你返回在矩阵主对角线上的元素和副对角线上且不在主对角线上元素的和。
示例 1:
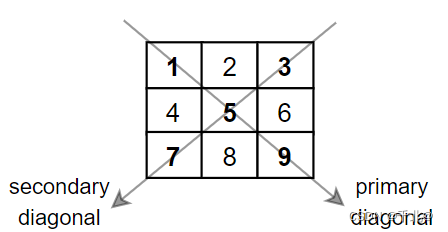
输入:mat = [[1,2,3],[4,5,6],[7,8,9]]
输出:25
解释:对角线的和为:1 + 5 + 9 + 3 + 7 = 25
请注意,元素 mat[1][1] = 5 只会被计算一次。
示例 2:
输入:mat = [[1,1,1,1],[1,1,1,1],[1,1,1,1],[1,1,1,1]]
输出:8
示例 3:
输入:mat = [[5]]
输出:5
提示:
- n == mat.length == mat[i].length
- 1 <= n <= 100
- 1 <= mat[i][j] <= 100
方法一:遍历矩阵
思路与算法
我们知道矩阵中某个位置 (i, j) 处于对角线上,则一定满足下列条件之一:
- i = j;
- i + j = n − 1;
根据上述结论,我们可以遍历整个矩阵,如果当前坐标 (i, j) 满足 i = j 或者 i + j = n − 1 则表示该位置一定在对角线上,则把当前的数字加入到答案之中。
代码:
class Solution {
public:int diagonalSum(vector<vector<int>>& mat) {int n = mat.size(), sum = 0;for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {if (i == j || i + j == n - 1) {sum += mat[i][j];}}}return sum;}
};
时间 12ms 击败 77.20%使用 C++ 的用户
内存 10.61mb 击败 89.00%使用 C++ 的用户
复杂度分析
- 时间复杂度:O(n2),其中 n 是矩阵 mat 的行数。
- 空间复杂度:O(1)。
方法二:枚举对角线元素
思路与算法
逐行遍历,记当前的行号为 i,则当前行中处于对角线的元素为: 坐标 (i, i) 和坐标 (i, n − i − 1),因此我们把 (i, i) 与 (i, n − i − 1) 处的数字加入到答案中。 如果 n 是奇数的话,则主对角线与副对角线存在交点 (⌊ n 2 n \over 2 2n⌋, ⌊ n 2 n \over 2 2n⌋),该点会被计算两次。所以当 n 为奇数的时候,需要减掉交点处的值。
代码:
class Solution {
public:int diagonalSum(vector<vector<int>>& mat) {int n = mat.size(), sum = 0, mid = n / 2;for (int i = 0; i < n; ++i) {sum += mat[i][i] + mat[i][n - 1 - i];}return sum - mat[mid][mid] * (n & 1);}
};
时间 12ms 击败 77.20%使用 C++ 的用户
内存 10.68mb 击败 54.80%使用 C++ 的用户
复杂度分析
- 时间复杂度:O(n),其中 n 是矩阵 mat 的行数。
- 空间复杂度:O(1)。
author:力扣官方题解
相关文章:

【1572. 矩阵对角线元素的和】
来源:力扣(LeetCode) 描述: 给你一个正方形矩阵 mat,请你返回矩阵对角线元素的和。 请你返回在矩阵主对角线上的元素和副对角线上且不在主对角线上元素的和。 示例 1: 输入:mat [[1,2,3]…...

GaussDB 开发篇+Java调用JDBC访问openGauss数据库
★ 数据库信息 ✔ 数据库版本:openGauss 5.0.0 ✔ 数据库端口:5432 ✔ 数据库名称:db_zzt ★ Java代码 package PAC_001;import java.sql.Connection; import java.sql.DriverManager; import java.sql.PreparedStatement; import java.sq…...

钕铁硼永磁材料基本概念
目录 一、何为磁性材料二、永磁材料的主要性能三、永磁材料的历史四、永磁材料的分类五、钕铁硼永磁材料5.1 产业链5.2 生产工艺 之前也写过其他行业的一些生产过程和工艺流程,大家有兴趣的可以翻翻以前的文章。 一、何为磁性材料 参加过九年义务教育的同学应该都知…...
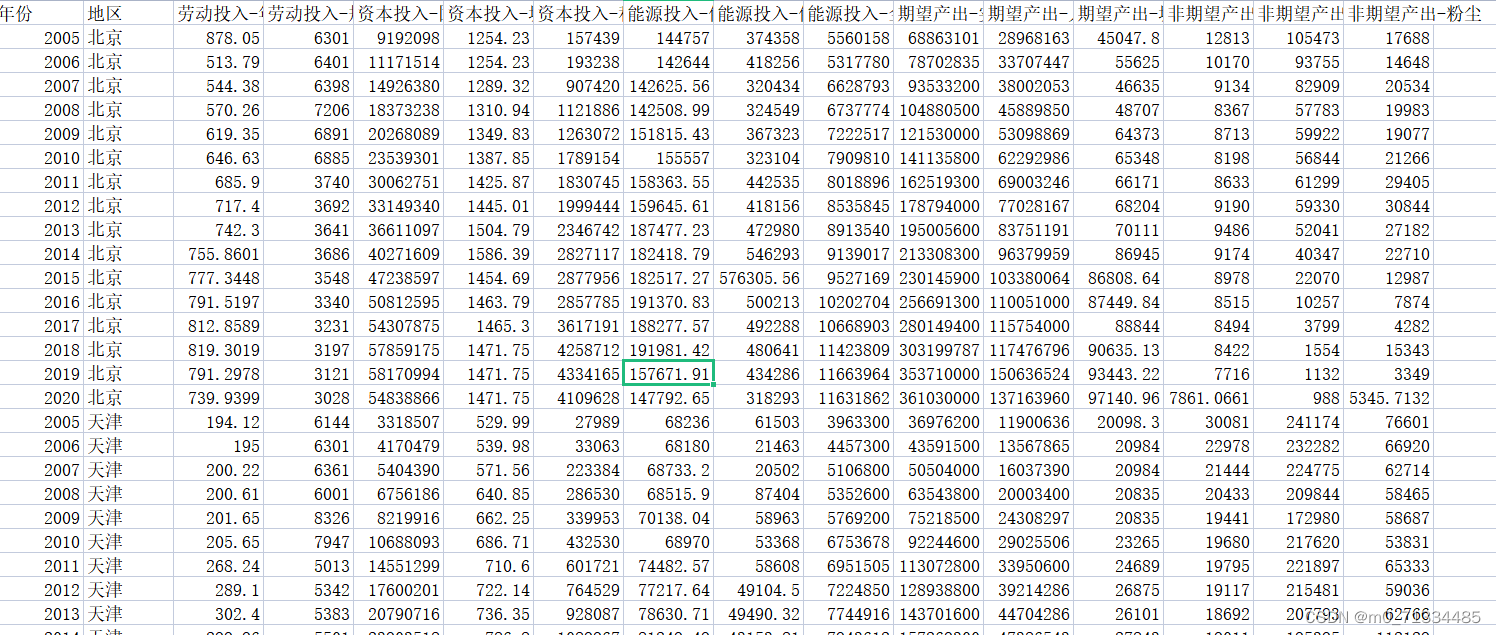
2005-2020年280个地级市绿色全要素生产率测算原始数据
2005-2020年280个地级市绿色全要素生产率测算原始数据 1、时间:2005-2020年 2、来源:中国城市统计年鉴、中国区域统计年鉴、中国能源年鉴、中国环境年鉴等 3、范围:280个地级市 4、指标:年末单位从业人员数、规模以上工业企业…...
电流的测量(反馈电流表)
另一方面,反馈电流表使用不同的方法来产生电流测量(见图 3)。他们使用有源跨阻放大器将电流转换为电压读数。电压输出是电流输入的倒数乘以反馈电阻器 R F的值。 V输出 -I输入* R F 图 3. 反馈电流表方法使用有源跨阻放大器将电流转换为…...
白帽黑帽与linux安全操作
目录 白帽黑帽 Linux安全 白帽黑帽 白帽(White Hat)和黑帽(Black Hat)通常用于描述计算机安全领域中的两种不同角色。白帽黑客通常被认为是合法的安全专家,他们通过合法途径寻找和修复安全漏洞,帮助企业和…...
【TypeScript】进阶之路语法细节,类型和函数
进阶之路 类型别名(type)的使用接口(interface)的声明的使用二者区别: 联合类型和交叉类型联合类型交叉类型 类型断言获取DOM元素 非空类型断言字面量类型的使用类型缩小(类型收窄)TypeScript 函数类型函数类型表达式内部规则检测函数的调用签…...
)
每日一题 611有效三角形的个数(相向双指针)
题目 给定一个包含非负整数的数组 nums ,返回其中可以组成三角形三条边的三元组个数。 示例 1: 输入: nums [2,2,3,4] 输出: 3 解释:有效的组合是: 2,3,4 (使用第一个 2) 2,3,4 (使用第二个 2) 2,2,3示例 2: 输入: nums [4,2,3,4] 输出: 4 题解 class Solu…...
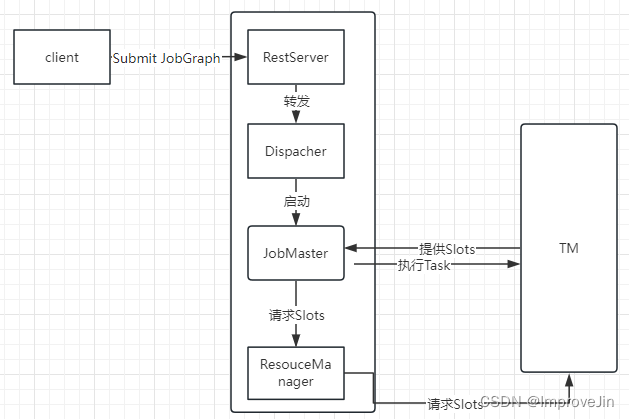
Flink源码之JobMaster启动流程
Flink中Graph转换流程如下: Flink Job提交时各种类型Graph转换流程中,JobGraph是Client端形成StreamGraph后经过Operator Chain优化后形成的,然后提交给JobManager的Restserver,最终转发给JobManager的Dispatcher处理。 Completa…...

C#,数值计算——抛物线插值与Brent方法(Parabolic Interpolation and Brent‘s Method)的计算方法与源程序
using System; namespace Legalsoft.Truffer { /// <summary> /// 抛物线插值与Brent方法 /// Parabolic Interpolation and Brents Method /// </summary> public class Brent : Bracketmethod { public double xmin { get; set…...
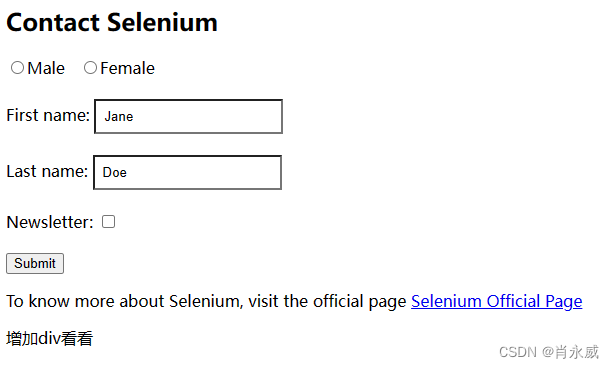
基于Selenium技术方案的爬取界面内容实践
1. 定位页面(多窗口切换) WebDriver提供了处理多个窗口的能力,这是通过使用“WebDriver.switchTo.window()”方法来切换到已知名称的窗口来实现的。如果名称未知,您可以使用“WebDriver.getWindowHandles()”获取已知窗口列表。您…...
)
线程记录(1)
创建线程: 一、1.继承Thread,重写run(),将操作写入其中 2.创建子类对象,start() 二、1.实现runnable接口,实现run() 2.创建子类对象,将子类对象作为参数传递到thread的构造器中,创建出Thread类…...

requests
操作步骤 安装 requests 发送GET请求 发送POST请求 说明: data: 参数接收form表单数据,后台会⾃动附加form表单请求信息头(data数据格式为字典) json:参数接收json数据,后台会⾃动附加json表单请求信息头&…...

Python 监控 Windows 服务
Python 监控 Windows 服务 Python 在 Windows 系统上可以使用 wmi 模块来实现对 Windows 服务的监控。本文将介绍如何使用 Python 监控 Windows 服务,并实现服务状态的查询和服务启停功能。 安装依赖 在使用 wmi 模块之前,需要先安装 wmi包。可以使用…...
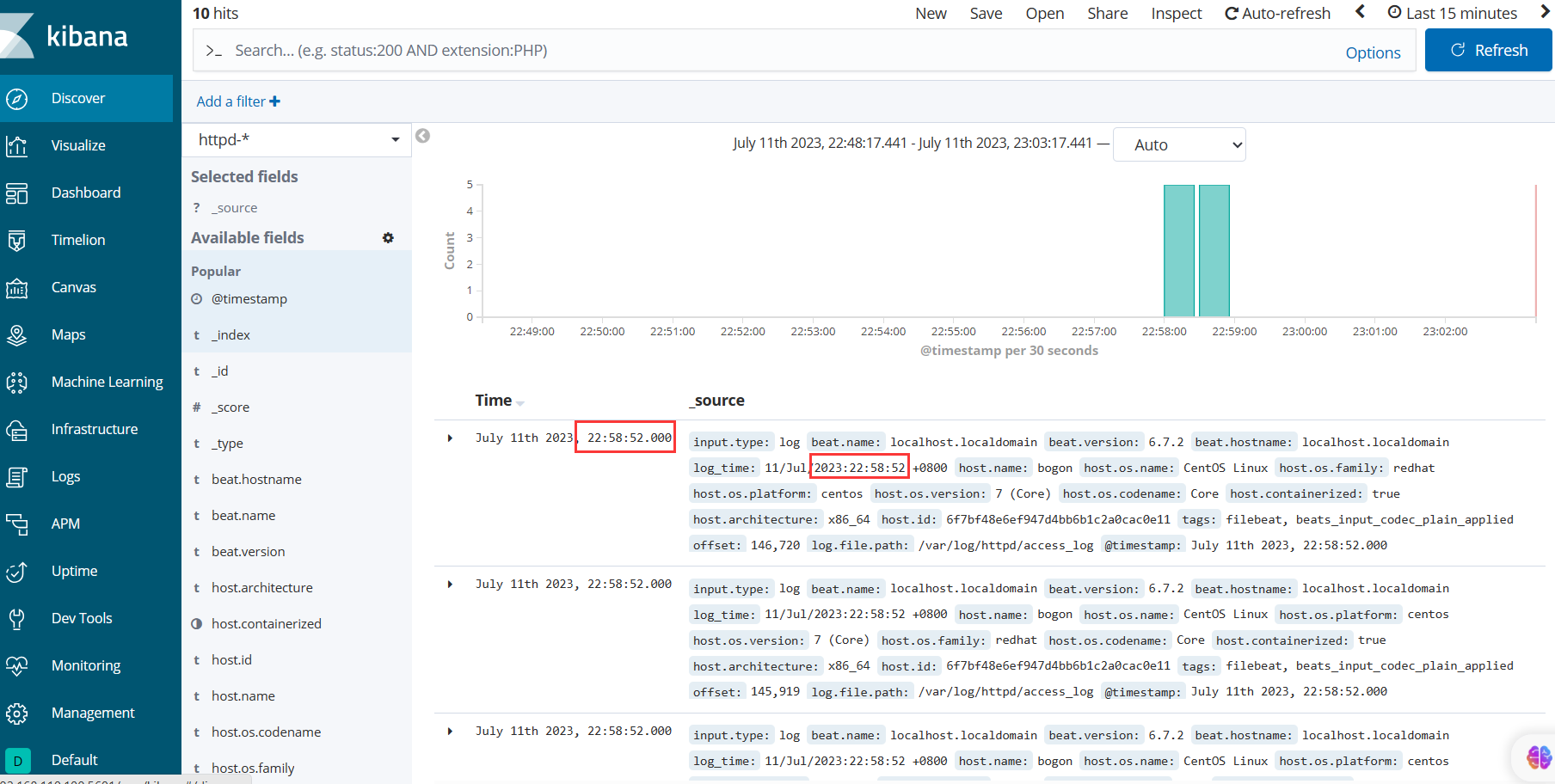
ELK中grok插件、mutate插件、multiline插件、date插件的相关配置
目录 一、grok 正则捕获插件 自定义表达式调用 二、mutate 数据修改插件 示例: ●将字段old_field重命名为new_field ●添加字段 ●将字段删除 ●将filedName1字段数据类型转换成string类型,filedName2字段数据类型转换成float类型 ●将filedNam…...
【C#】静默安装、SQL SERVER静默安装等
可以通过cmd命令行来执行,也可以通过代码来执行,一般都需要管理员权限运行 代码 /// <summary>/// 静默安装/// </summary>/// <param name"fileName">安装文件路径</param>/// <param name"arguments"…...

在vue3中定义组件的5种方式
在vue3中定义组件的5种方式 Vue 正在不断发展,目前在 Vue3 中定义组件的方法有多种。从选项式到组合式再到类API,情况截然不同。本文将会定义一个简单的组件并使用所有可用的方法重构它。 选项式 这是在 Vue 中声明组件的最常见方法。从 Vue1 就开始存…...

算法训练营题目,忘了第几天了
144. 二叉树的前序遍历 给你二叉树的根节点 root ,返回它节点值的 前序 遍历。 输入:root [1,null,2,3] 输出:[1,2,3] var res[]int func preorderTraversal(root *TreeNode) []int {res []int{}traval(root)return res }func traval(no…...

蓝桥杯-统计子矩阵
统计子矩阵 题目链接 思路: 使用前缀和滑动窗口 ,可以先计算出纵向或横向的前缀和,matrix[i][j]表示前i行第j列之和 然后遍历上边界top和下边界buttom,再这个上下边界内使用滑动窗口,由于前面维护了纵向前缀和&…...

在线预览Word、Excel、PowerPoint等文件
在我们工作时,经常会有在线查看各种不同类型的文件的需要,如Word文档、Excel表格、PowerPoint幻灯片和PDF等。可以直接在这里预览:https://www.compdf.com/webviewer/demo Word 文件实现前端预览 方案一: 使用 XDOC 可以实现预…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...
