⌈算法进阶⌋图论::并查集——快速理解到熟练运用
目录
一、原理
1. 初始化Init
2. 查询 find
3. 合并 union
二、代码模板
三、练习
1、 990.等式方程的可满足性🟢
2、 1061. 按字典序排列最小的等效字符串🟢
3、721.账户合并 🟡
4、 839.相似字符串组🟡
5、 2812.找出最安全路径 🔴
一、原理
并查集主要运用与求一些不相交且有关联的集合的合并,这一点我们从后面的例题中进一步理解,我们首先掌握并查集的原理和运用
并查集的主要操作有:
1. 初始化Init
我们将每个数据看作一个树的节点,初始化每个节点指针指向自己
我们用一个数组fa[]的下标index表示节点, 用fa[index]表示该节点的根节点;
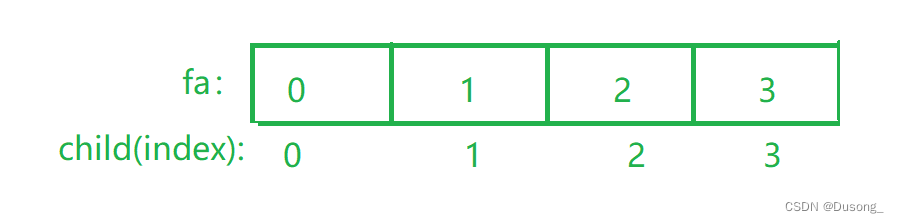
2. 查询 find
查询一个节点的根节点,以用于其他操作;
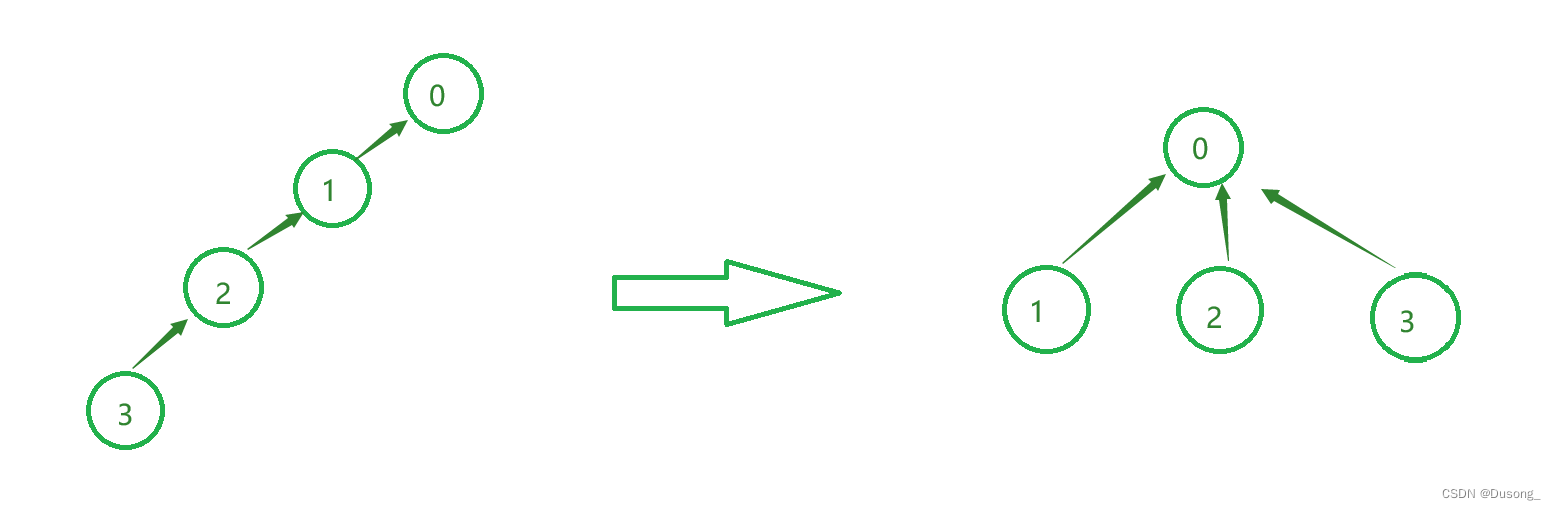
如上图, 若要查询数据3所在的集合的根节点,想做图这样的链接方式每次查询需要O(n)的时间,我们需要在查询时将树的结构转换成右图所示,这样之后的每次查询时间复杂度为O(logn)
3. 合并 union
实现两个集合的合并,可以抽象成两颗树的合并,即将两颗树的根节点相连;
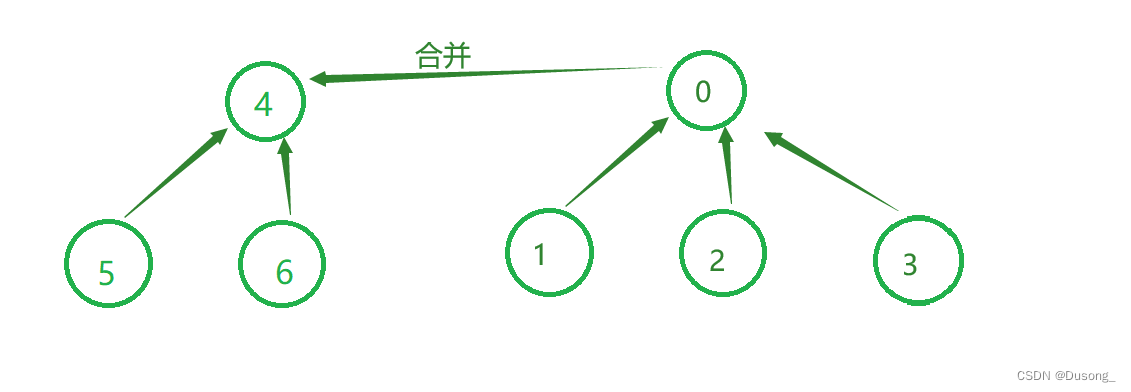
二、代码模板
//初始化
vector<int> fa(n* n);
iota(fa.begin(), fa.end(), 0);//查询
function<int(int)> find = [&](int x) -> int { return x == fa[x] ? x : fa[x] = find(fa[x]); }; //合并
fa[find(x)] = find(y); 三、练习
1、 990.等式方程的可满足性🟢
给定一个由表示变量之间关系的字符串方程组成的数组,每个字符串方程
equations[i]的长度为4,并采用两种不同的形式之一:"a==b"或"a!=b"。在这里,a 和 b 是小写字母(不一定不同),表示单字母变量名。只有当可以将整数分配给变量名,以便满足所有给定的方程时才返回
true,否则返回false。
解题思路:合并等式方程两侧字母,运用并查集管理相等字母集合
class Solution {
public:bool equationsPossible(vector<string>& equations) {//初始化vector<int> fa(26);iota(fa.begin(), fa.end(), 0);//查询function<int(int)> find = [&](int x) -> int { return fa[x] == x ? x : fa[x] = find(fa[x]); };for (auto s : equations) {if (s[1] == '=') {int x = s[0] - 97, y = s[3] - 97;fa[find(x)] = find(y); //相等则合并}}for (auto s : equations) {int x = s[0] - 97, y = s[3] - 97;if (s[1] == '!' && find(x) == find(y)) return false; //矛盾,返回false}return true;}
};2、 1061. 按字典序排列最小的等效字符串🟢
给出长度相同的两个字符串
s1和s2,还有一个字符串baseStr。其中
s1[i]和s2[i]是一组等价字符。
- 举个例子,如果
s1 = "abc"且s2 = "cde",那么就有'a' == 'c', 'b' == 'd', 'c' == 'e'。等价字符遵循任何等价关系的一般规则:
- 自反性 :
'a' == 'a'- 对称性 :
'a' == 'b'则必定有'b' == 'a'- 传递性 :
'a' == 'b'且'b' == 'c'就表明'a' == 'c'例如,
s1 = "abc"和s2 = "cde"的等价信息和之前的例子一样,那么baseStr = "eed","acd"或"aab",这三个字符串都是等价的,而"aab"是baseStr的按字典序最小的等价字符串利用
s1和s2的等价信息,找出并返回baseStr的按字典序排列最小的等价字符串。
解题思路:由等价关系可以一眼看出这道题使用并查集,s1与s2对应字母放入一个集合(即将其合并),最终找到baseStr每个字母对应的集合中的最小字典序字母
class Solution {
public:string smallestEquivalentString(string s1, string s2, string baseStr) {//初始化vector<int> fa(26);iota(fa.begin(), fa.end(), 0);//查询function<int(int)> find = [&](int x) -> int { return fa[x] == x ? x : fa[x] = find(fa[x]); };for (int i = 0; i < s1.size(); i++) {int x = s1[i] - 97, y = s2[i] - 97;fa[find(y)] = find(x); //合并}unordered_map<int, set<char>> g; //统计以根节点代表的一个集合中的所有节点for (int i = 0; i < 26; i++) {g[find(i)].insert(i + 97);}for (int i = 0; i < baseStr.size(); i++) {//利用set默认排升序的特点,找到baseStr[i]的根节点的集合中的最小字母baseStr[i] = *(g[find(baseStr[i] - 97)].begin()); }return baseStr;}
};3、721.账户合并 🟡
给定一个列表
accounts,每个元素accounts[i]是一个字符串列表,其中第一个元素accounts[i][0]是 名称 (name),其余元素是 emails 表示该账户的邮箱地址。现在,我们想合并这些账户。如果两个账户都有一些共同的邮箱地址,则两个账户必定属于同一个人。请注意,即使两个账户具有相同的名称,它们也可能属于不同的人,因为人们可能具有相同的名称。一个人最初可以拥有任意数量的账户,但其所有账户都具有相同的名称。
合并账户后,按以下格式返回账户:每个账户的第一个元素是名称,其余元素是 按字符 ASCII 顺序排列 的邮箱地址。账户本身可以以 任意顺序 返回。
解题思路:根据题意,拥有相同邮箱的账户为同一人,最终需要将相同用户的邮箱合并到一起,同样也是一眼并查集,但是代码实现起来可能有些复杂;首先需要遍历所有邮箱,判断是否有重复,将拥有同一邮箱的用户合并,需要特别注意的是,用户名相同不代表是同一人,最终将属于同一集合的用户邮箱用set去重,返回结果;
class Solution {
public:vector<vector<string>> accountsMerge(vector<vector<string>>& accounts) {int n = accounts.size();//以accounts的下标[0, n)作为用户名字,方便以下标寻找父亲vector<int> fa(n);iota(fa.begin(), fa.end(), 0); //初始化function<int(int)> find = [&](int i) -> int { return fa[i] == i ? i : fa[i] = find(fa[i]); };//key:邮箱 val:名字unordered_map<string, vector<int>> email_name;for (int i = 0; i < n; i++) {for (int j = 1; j < accounts[i].size(); j++) { //遍历每个账户的所有邮箱email_name[accounts[i][j]].push_back(i);//如果同一个邮箱出现多个名字,那么认为为同一个人,此时连接if (email_name[accounts[i][j]].size() > 1) {fa[find(email_name[accounts[i][j]][0])] = find(i); //合并}}}//之前尝试用map,但是同一个名字可能不是同一人,所以map行不通//用set去重vector<set<string>> g(n);for (int i = 0; i < n; i++) {int f = find(i); //找到根节点,将邮箱插入到根节点的数组中for (int j = 1; j < accounts[i].size(); j++) {g[f].insert(accounts[i][j]); }}vector<vector<string>> ans;for (int i = 0; i < n; i++) {if (g[i].size() != 0) { vector<string> tmp = {g[i].begin(), g[i].end()}; //将set转vectortmp.insert(tmp.begin(), accounts[i][0]); //头插名字ans.push_back(tmp);}}return ans;}
};4、 839.相似字符串组🟡
如果交换字符串
X中的两个不同位置的字母,使得它和字符串Y相等,那么称X和Y两个字符串相似。如果这两个字符串本身是相等的,那它们也是相似的。例如,
"tars"和"rats"是相似的 (交换0与2的位置);"rats"和"arts"也是相似的,但是"star"不与"tars","rats",或"arts"相似。总之,它们通过相似性形成了两个关联组:
{"tars", "rats", "arts"}和{"star"}。注意,"tars"和"arts"是在同一组中,即使它们并不相似。形式上,对每个组而言,要确定一个单词在组中,只需要这个词和该组中至少一个单词相似。给你一个字符串列表
strs。列表中的每个字符串都是strs中其它所有字符串的一个字母异位词。请问strs中有多少个相似字符串组?
解题思路:暴力遍历+dfs查询相似字符串,将相似字符串合并,最终返回集合个数
class Solution {
public:int numSimilarGroups(vector<string>& strs) {int n = strs.size();//初始化vector<int> fa(n);iota(fa.begin(), fa.end(), 0);//查询function<int(int)> find = [&](int x) -> int { return x == fa[x] ? x : fa[x] = find(fa[x]); }; int vis[n];memset(vis, 0, sizeof(vis));//dfsfunction<void(int)> is_same = [&](int i) -> void {vis[i] = true;string& s1 = strs[i];for (int j = 0; j < n; j++) {if (!vis[j]) {string& s2 = strs[j];if (s1 == s2) { //相同字符串相似,直接合并fa[find(j)] = fa[i];is_same(j);} else {int dif = 0;for (int k = 0; k < s1.size(); k++) {if (s1[k] != s2[k]) dif++;if (dif > 2) break;}if (dif == 2) { //恰有两个位置字符不同则相似,合并fa[find(j)] = fa[i];is_same(j);}}}}};//dfs入口for (int i = 0; i < n; i++) {if(!vis[i]) is_same(i);}//用set去重,返回集合个数set<int> ans;for (int i = 0; i < n; i++) ans.insert(find(i)); //将根节点插入set中return ans.size();}
};5、 2812.找出最安全路径 🔴
给你一个下标从 0 开始、大小为
n x n的二维矩阵grid,其中(r, c)表示:
- 如果
grid[r][c] = 1,则表示一个存在小偷的单元格- 如果
grid[r][c] = 0,则表示一个空单元格你最开始位于单元格
(0, 0)。在一步移动中,你可以移动到矩阵中的任一相邻单元格,包括存在小偷的单元格。矩阵中路径的 安全系数 定义为:从路径中任一单元格到矩阵中任一小偷所在单元格的 最小 曼哈顿距离。
返回所有通向单元格
(n - 1, n - 1)的路径中的 最大安全系数 。单元格
(r, c)的某个 相邻 单元格,是指在矩阵中存在的(r, c + 1)、(r, c - 1)、(r + 1, c)和(r - 1, c)之一。两个单元格
(a, b)和(x, y)之间的 曼哈顿距离 等于| a - x | + | b - y |,其中|val|表示val的绝对值。
解题思路:由题,求从左上角到右下角路径中的最小安全系数的最大值:倒序枚举答案(安全系数), 将>=当前安全系数的坐标用并查集相连(合并),一次循环结束判断左上角与右下角是否相连
class Solution {
public:static constexpr int dirs[5] = {1, 0, -1, 0, 1};int maximumSafenessFactor(vector<vector<int>>& grid) {int n = grid.size();vector<pair<int, int>> q;vector<vector<int>> dis(n, vector<int>(n, -1));for (int i = 0; i < n; i++) {for (int j = 0;j < n; j++) {if(grid[i][j] == 1) {q.push_back({i, j});dis[i][j] = 0;}}}//bfs求每个点安全系数,及不同安全系数的值的下标(用于后续并查集的合并)vector<vector<pair<int, int>>> groups = {q};while (!q.empty()) {int safe = groups.size();vector<pair<int, int>> tmp;for (auto &[i, j] : q) {for (int k = 0; k < 4; k++) {int x = i + dirs[k], y = j + dirs[k + 1];if (x >= 0 && x < n && y >= 0 && y < n && dis[x][y] < 0) {dis[x][y] = safe;tmp.push_back({x, y});}}}if (tmp.size() > 0)groups.push_back(tmp);q = move(tmp);}//初始化vector<int> fa(n*n);for (int i = 0; i < n * n; i++) fa[i] = i;//查询function<int(int)> find = [&](int x) -> int { return x == fa[x] ? x : fa[x] = find(fa[x]); };for (int ans = groups.size() - 1; ans > 0; ans--) {for (auto& [i, j] : groups[ans]) {for (int k = 0; k < 4; k++) {int x = i + dirs[k], y = j + dirs[k + 1];if (x >= 0 && x < n && y >= 0 && y < n && dis[x][y] >= dis[i][j]) fa[find(x * n + y)] = find(i * n + j); //合并}}if (find(0) == find((n - 1) * n + n - 1)) return ans; //相通则返回答案}return 0;}
};相关文章:

⌈算法进阶⌋图论::并查集——快速理解到熟练运用
目录 一、原理 1. 初始化Init 2. 查询 find 3. 合并 union 二、代码模板 三、练习 1、 990.等式方程的可满足性🟢 2、 1061. 按字典序排列最小的等效字符串🟢 3、721.账户合并 🟡 4、 839.相似字符串组🟡 5、 2812.找出最安全…...

【ROS】fsd_algorithm架构学习与源码分析(致敬)
😏★,:.☆( ̄▽ ̄)/$:.★ 😏 这篇文章主要介绍fsd_algorithm架构学习与源码分析。 无专精则不能成,无涉猎则不能通。——梁启超 欢迎来到我的博客,一起学习,共同进步。 喜欢的朋友可以关注一下&am…...
PHP最简单自定义自己的框架定义常量自动生成目录(三)
1、框架入口增加模块定义,实现多模块功能 index.php 定义模块 <?php //定义当前请求模块 define("MODULE",index); require "./core/KJ.php"; 创建后台模块admin.php <?php define("MODULE",admin); require "./cor…...
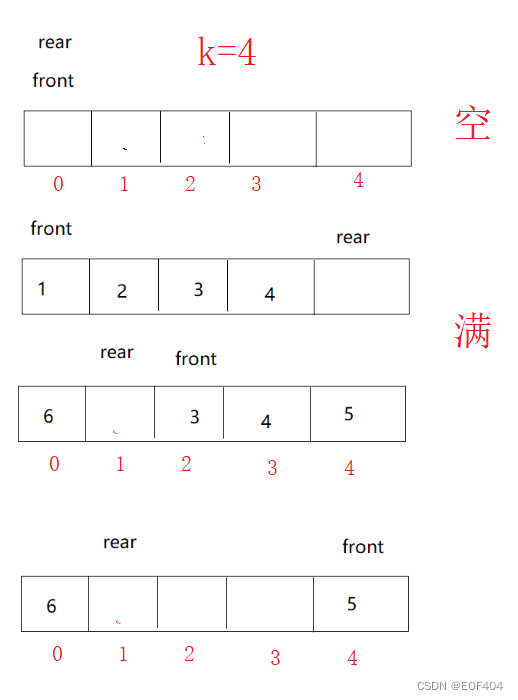
栈和队列详解
目录 栈 栈的概念及结构: 栈的实现: 代码实现: Stack.h stack.c 队列: 概念及结构: 队列的实现: 代码实现: Queue.h Queue.c 拓展: 循环队列(LeetCode题目链接࿰…...
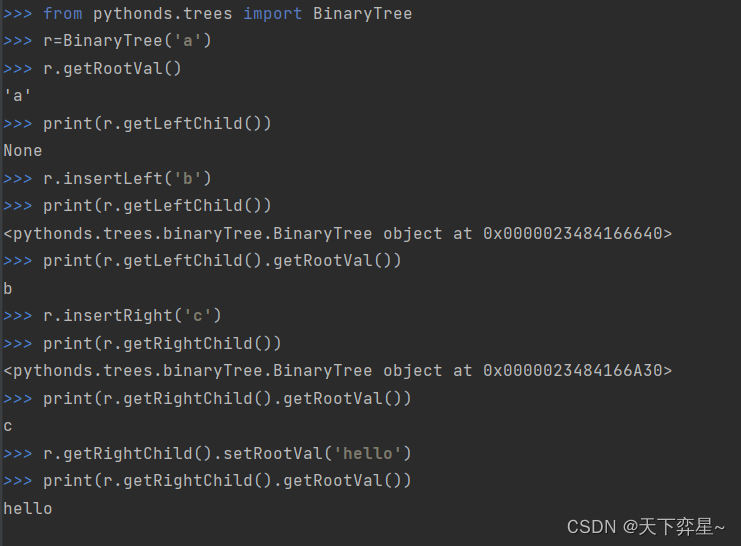
数据结构 | 树的定义及实现
目录 一、树的术语及定义 二、树的实现 2.1 列表之列表 2.2 节点与引用 一、树的术语及定义 节点: 节点是树的基础部分。它可以有自己的名字,我们称作“键”。节点也可以带有附加信息,我们称作“有效载荷”。有效载荷信息对于很多树算法…...
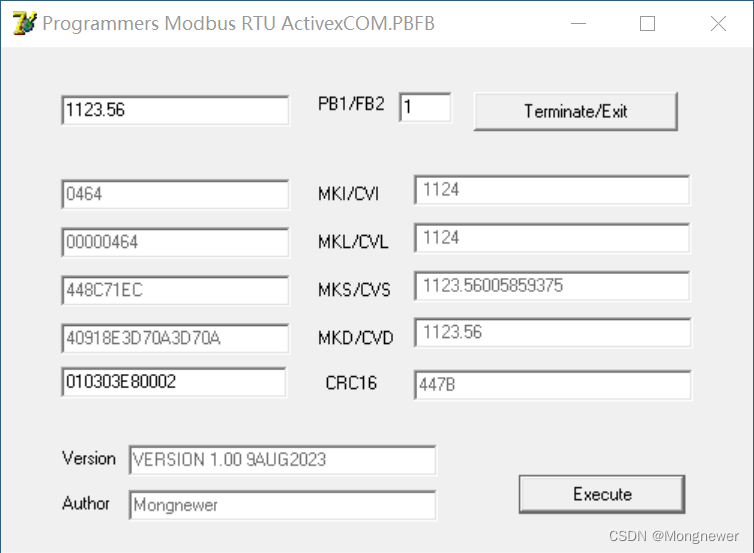
Delphi7通过VB6之COM对象调用FreeBASIC写的DLL功能
VB6写ActiveX COM组件比较方便,不仅PowerBASIC与VB6兼容性好,Delphi7与VB6兼容性也不错,但二者与FreeBASIC兼容性在字符串处理上差距比较大,FreeBASIC是C化的语言,可直接使用C指令。下面还是以实现MKI/CVI, MKL/CVL, M…...
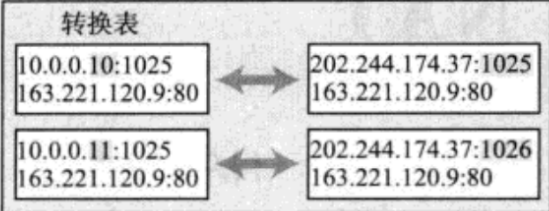
【Linux 网络】NAT技术——缓解IPv4地址不足
NAT技术 NAT 技术背景NAT IP转换过程NAPTNAT 技术的缺陷 NAT(Network Address Translation,网络地址转换)技术,是解决IP地址不足的主要手段,并且能够有效地避免来自网络外部的攻击,隐藏并保护网络内部的计算…...
协议)
Flink 两阶段提交(Two-Phase Commit)协议
Flink 两阶段提交(Two-Phase Commit)是指在 Apache Flink 流处理框架中,为了保证分布式事务的一致性而采用的一种协议。它通常用于在流处理应用中处理跨多个分布式数据源的事务性操作,确保所有参与者(数据源或计算节点…...

【Docker晋升记】No.2 --- Docker工具安装使用、命令行选项及构建、共享和运行容器化应用程序
文章目录 前言🌟一、Docker工具安装🌟二、Docker命令行选项🌏2.1.docker run命令选项:🌏2.2.docker build命令选项:🌏2.3.docker images命令选项:🌏2.4.docker ps命令选项…...

[OnWork.Tools]系列 00-目录
OnWork.Tools系列文章目录 OnWork.Tools系列 01-简介_末叶的博客-CSDN博客OnWork.Tools系列 02-安装_末叶的博客-CSDN博客OnWork.Tools系列 03-软件设置_末叶的博客-CSDN博客OnWork.Tools系列 04-快捷启动_末叶的博客-CSDN博客OnWork.Tools系列 05-系统工具_末叶的博客-CSDN博…...

Cadvisor+InfluxDB+Grafan+Prometheus(详解)
目录 一、CadvisorInfluxDBGrafan案例概述 (一)Cadvisor Cadvisor 产品特点: (二)InfluxDB InfluxDB应用场景: InfluxDB主要功能: InfluxDB主要特点: (三&#…...
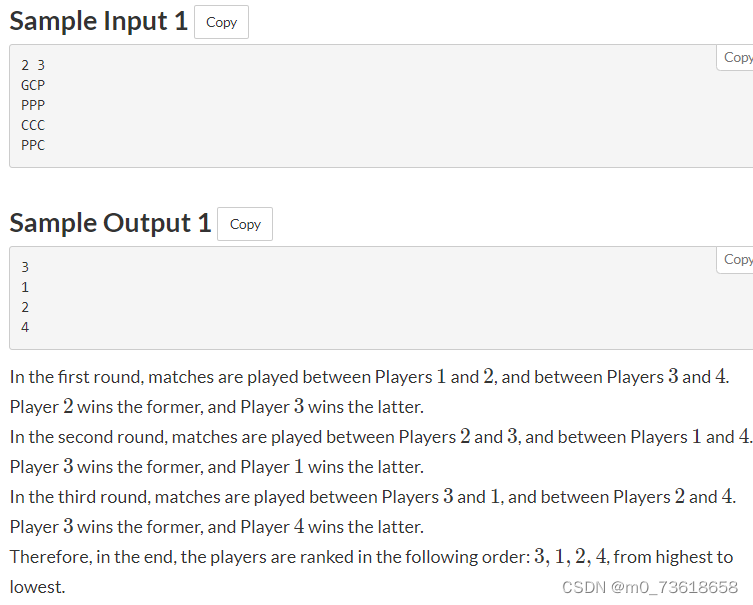
AtcoderABC222场
A - Four DigitsA - Four Digits 题目大意 给定一个整数N,其范围在0到9999之间(包含边界)。在将N转换为四位数的字符串后,输出它。如果N的位数不足四位,则在前面添加必要数量的零。 思路分析 可以使用输出流的格式设…...
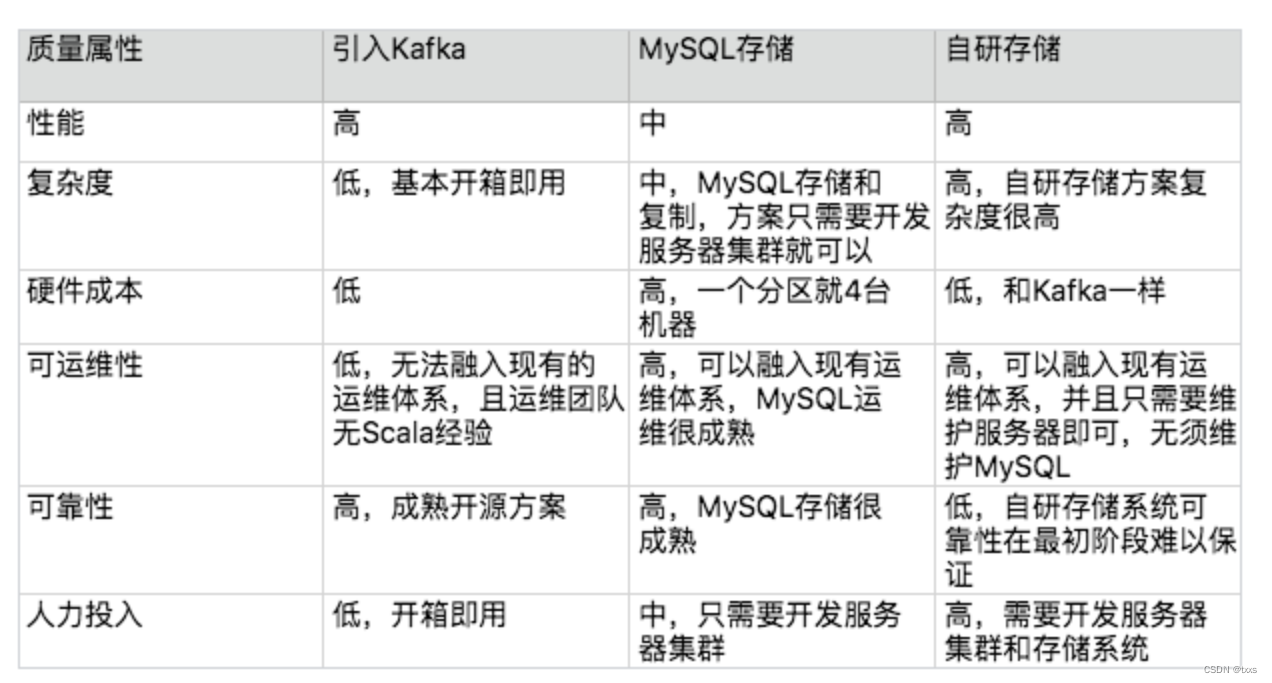
架构实践方法
一、识别复杂度 将主要的复杂度问题列出来,然后根据业务、技术、团队等综合情况进行排序,优先解决当前面临的最主要的复杂度问题。对于按照复杂度优先级解决的方式,存在一个普遍的担忧:如果按照优先级来解决复杂度,可…...
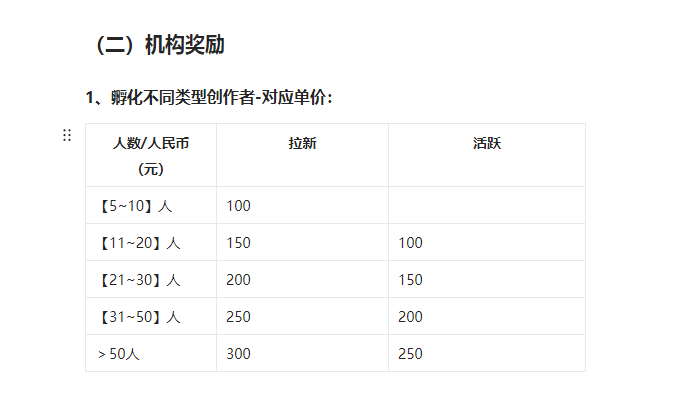
点淘的MCN机构申请详细入驻指南!
消费趋势的变化,来自消费人群的变化。 后疫情时代,经济复苏的反弹力度不足,人们开始怀疑我们正从前几年的消费升级,跌入消费降级的时代,但这并不能准确概括消费市场的变化。 仔细翻看各大奢侈品集团的财报࿰…...
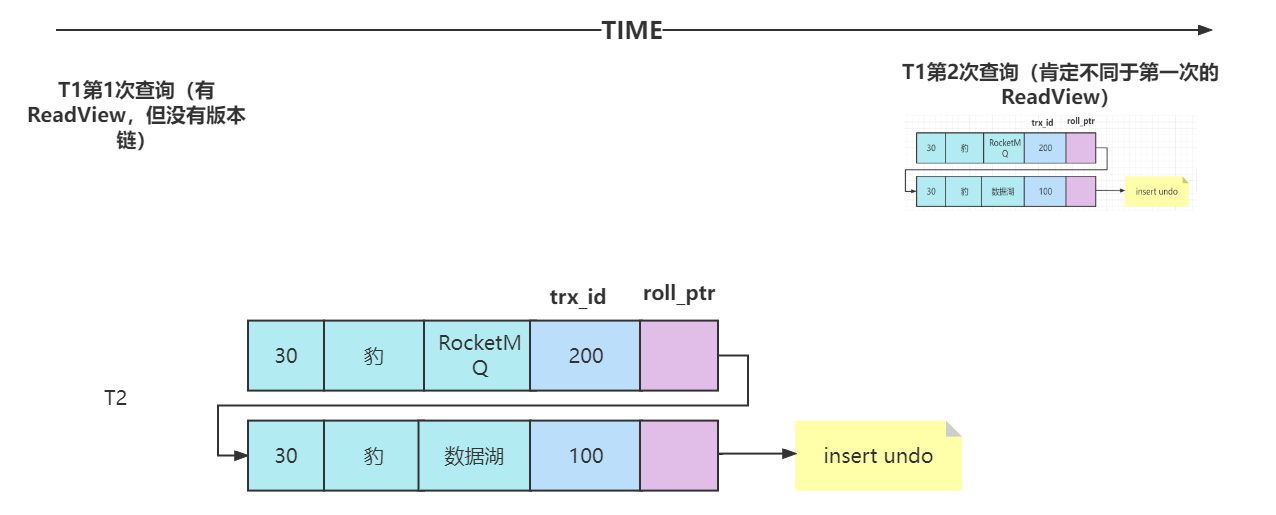
事务和事务的隔离级别
1.4.事务和事务的隔离级别 1.4.1.为什么需要事务 事务是数据库管理系统(DBMS)执行过程中的一个逻辑单位(不可再进行分割),由一个有限的数据库操作序列构成(多个DML语句,select语句不包含事务&…...
)
每日一题 34在排序数组中查找元素的第一个和最后一个位置(二分查找)
题目 给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。 如果数组中不存在目标值 target,返回 [-1, -1]。 你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。 示例 1&…...
Spring Boot Admin 环境搭建与基本使用
Spring Boot Admin 环境搭建与基本使用 一、Spring Boot Admin是什么二、提供了那些功能三、 使用Spring Boot Admin3.1搭建Spring Boot Admin服务pom文件yml配置文件启动类启动admin服务效果 3.2 common-apipom文件feignhystrix 3.3服务消费者pom文件yml配置文件启动类control…...
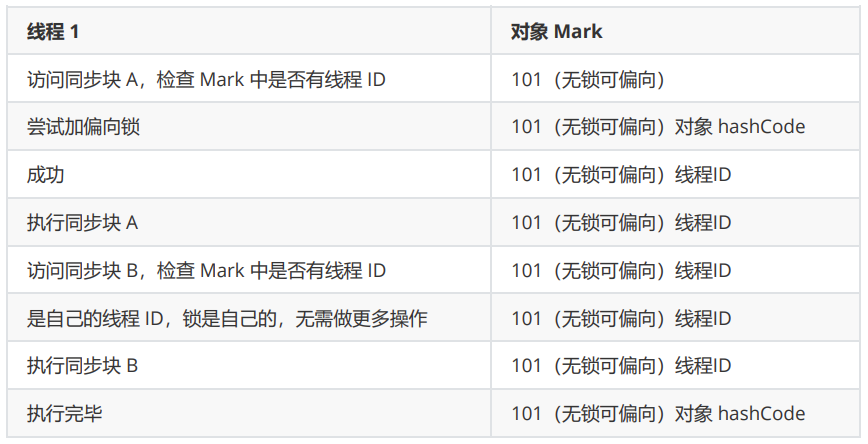
JVM之内存模型
1. Java内存模型 很多人将Java 内存结构与java 内存模型傻傻分不清,java 内存模型是 Java Memory Model(JMM)的意思。 简单的说,JMM 定义了一套在多线程读写共享数据时(成员变量、数组)时,对数据…...

音视频 vs2017配置FFmpeg
vs2017 ffmpeg4.2.1 一、首先我把FFmpeg整理了一下,放在C盘 二、新建空项目 三、添加main.cpp,将bin文件夹下dll文件拷贝到cpp目录下 #include<stdio.h> #include<iostream>extern "C" { #include "libavcodec/avcodec.h&…...

【项目管理】PMP备考宝典-第二章《环境》
第一节:概述 1.项目所处的组织环境 (1)事业环境因素(EEFs) 组织内部的事业环境因素: 企业都会有愿景、使命、价值观,这些决定了企业的发展方向。不忘初心,坚定地走自己的路&#…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...
