最后一击
第二届上海市青少年算法竞赛(小学组)
题目描述 Description
小爱和小艾两人组队打一只怪兽。一开始怪兽有 n 点生命值,当 n 变成 0 或更低时,怪兽就被消灭了。他们两人是同时开始攻击的,小爱每分钟可以攻击 a 下,小艾每分钟可以攻击 b 下。若 a=2,b=4,则小爱发出攻击的时刻为
0.5, 1, 1.5, 2, 2.5, ⋯
小艾发出攻击的时刻为
0.25, 0.5, 0.75, 1, 1.25, 1.5, ⋯
攻击分两种类型,普通攻击每次对怪兽造成 1 点伤害。若在某时刻,小爱和小艾恰好一同发出攻击,称为爆击,爆击将对怪兽造成成倍的伤害,共计 (1+1)×2=4 点伤害。
一旦攻击开始,就不会中断,直到怪兽被消灭为止,请问,对怪兽造成最后一点伤害的是哪一位玩家?如果最后一击是两人同时造成的,输出 C(Combo的意思)。
输入描述 Input Description
第一行:一个正整数表示 n。
第二行:两个正整数表示 a 与 b。
输出描述 Output Description
1.若是小爱发出了最后一击,输出 A;
2.若是小艾发出了最后一击,输出 B;
3.若是两人的爆击为最后一击,输出 C。
样例输入 Sample Input
输入样例1: 40 3 5 ---------- 输入样例2: 33 3 5
样例输出 Sample Output
输出样例1: C ---------- 输出样例2: B
数据范围及提示 Data Size & Hint
数据范围提示:
对于 50% 的数据,1≤n≤100,1≤a,b≤10;
对于 100% 的数据,1≤n≤20000000,1≤a,b≤40000;
代码:
#include<iostream>
using namespace std;
int n,a,b;
int ap=0;
int bp=0;int main() {cin>>n>>b>>a;while (n>0){if (ap+a<bp+b){ap+=a;n--;}else if(ap+a>bp+b){bp+=b;n--;}else {ap+=a;bp+=b;n-=4;}if(ap>1e9&&bp>1e9){ap-=1e9;bp-=1e9;}}if (ap>bp){cout<<"A";}else if (bp>ap){cout<<"B";}else{cout<<"C";}return 0;
}没事干压缩一下:
#include<iostream>
using namespace std;int n,a,b;int ap=0;int bp=0;int main() {cin>>n>>b>>a;while (n>0){if (ap+a<bp+b){ap+=a;n--;}else if(ap+a>bp+b){bp+=b;n--;}else {ap+=a;bp+=b;n-=4;}if(ap>1e9&&bp>1e9){ap-=1e9;bp-=1e9;}}if (ap>bp){cout<<"A";}else if (bp>ap){cout<<"B";}else{cout<<"C";}return 0;}相关文章:

最后一击
第二届上海市青少年算法竞赛(小学组) 题目描述 Description 小爱和小艾两人组队打一只怪兽。一开始怪兽有 n 点生命值,当 n 变成 0 或更低时,怪兽就被消灭了。他们两人是同时开始攻击的,小爱每分钟可以攻击 a 下&…...

K8S资源管理方式
K8S资源管理方式 文章目录 K8S资源管理方式一、陈述式资源管理1.基础命令操作2.创建pod3.查看资源状态4.查看pod中的容器日志5.进入pod中的容器6.删除pod资源7.pod扩容8.项目生命周期管理(创建-->发布-->更新-->回滚-->删除)8.1创建services…...
第三章 图论 No.9有向图的强连通与半连通分量
文章目录 定义Tarjan求SCC1174. 受欢迎的牛367. 学校网络1175. 最大半连通子图368. 银河 定义 连通分量是无向图的概念,yxc说错了,不要被误导 强连通分量:在一个有向图中,对于分量中的任意两点u,v,一定能从…...

回归预测 | MATLAB实现基于PSO-LSSVM-Adaboost粒子群算法优化最小二乘支持向量机结合AdaBoost多输入单输出回归预测
回归预测 | MATLAB实现基于PSO-LSSVM-Adaboost粒子群算法优化最小二乘支持向量机结合AdaBoost多输入单输出回归预测 目录 回归预测 | MATLAB实现基于PSO-LSSVM-Adaboost粒子群算法优化最小二乘支持向量机结合AdaBoost多输入单输出回归预测预测效果基本介绍模型描述程序设计参考…...

Mysql 和Oracle的区别
、mysql与oracle都是关系型数据库,Oracle是大型数据库,而MySQL是中小型数据库。但是MySQL是开源的,但是Oracle是收费的,而且比较贵。 1 2 mysql默认端口:3306,默认用户:root oracle默认端口&…...

在收藏夹里“积灰”的好东西——“收藏从未停止,行动从未开始”
方向一:分享一道你收藏的好题 小雅兰刚学数据结构与算法的时候,学的真的是很吃力,感觉链表真的特别的难,在学习了后面的知识之后,发现链表慢慢变得简单了,若是放在现在,小雅兰仍然觉得链表的知…...
【算法|数组】双指针
算法|数组——双指针 引入 给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。 示例 1: 输入:nums [-4,-1,0,3,10] 输出:[0,1,9,16,100] 解释:…...

asp.net core6 webapi 使用反射批量注入接口层和实现接口层的接口的类到ioc中
IBLL接口层类库 namespace IBLL {public interface ICar{string CarName();} } namespace IBLL {public interface IRed{string RedName();} }BLL实现接口层类库 namespace BLL {public class Car : ICar{public string CarName(){return "BBA";}} } namespace BLL…...

【2023】字节跳动 10 日心动计划——第九关
目录 1. 螺旋矩阵2. 划分字母区间3. 子集 II 1. 螺旋矩阵 🔗 原题链接:54. 螺旋矩阵 类似于BFS那样使用方向数组即可。 class Solution { public:vector<int> spiralOrder(vector<vector<int>>& matrix) {int m matrix.size(), …...
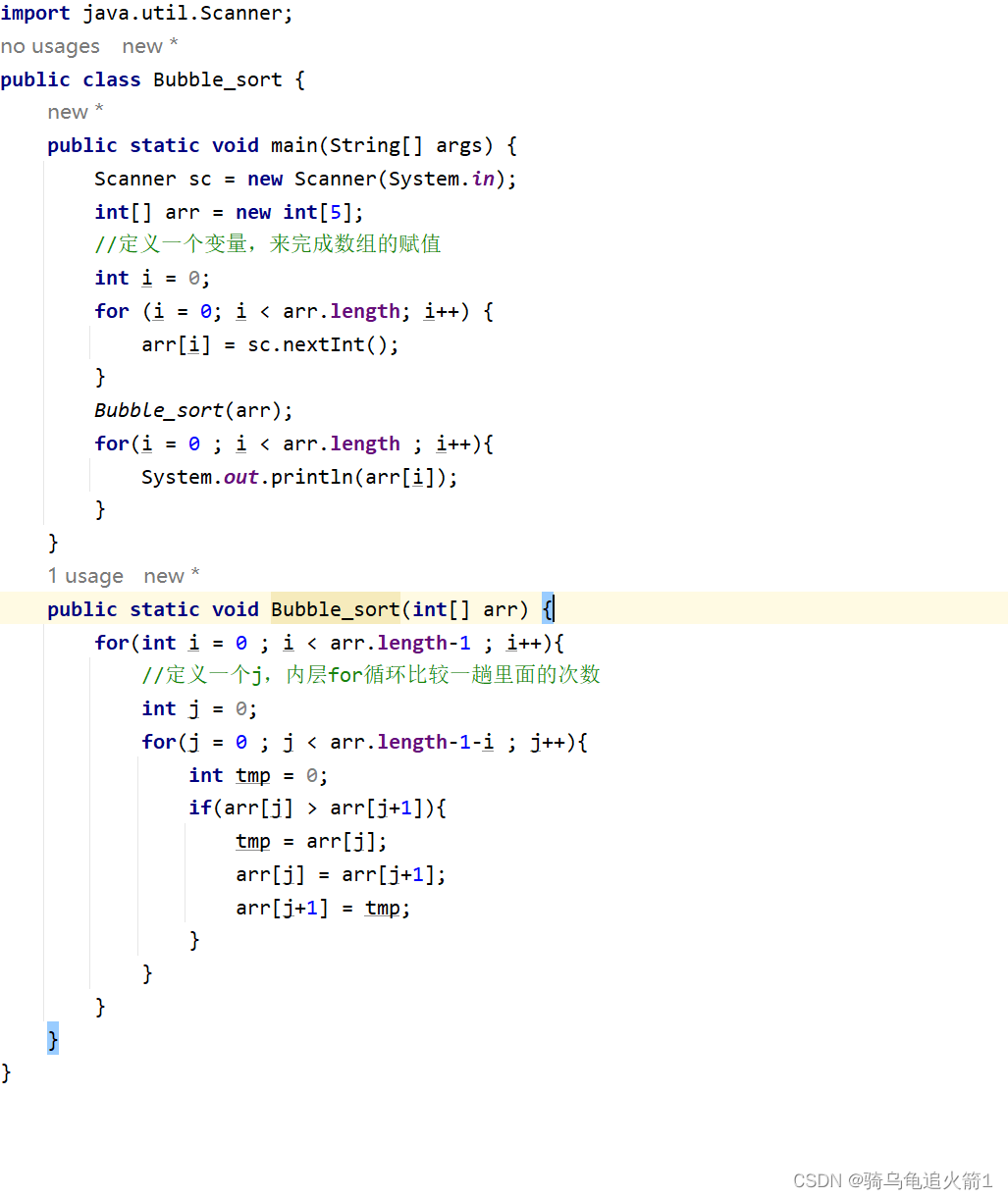
小龟带你敲排序之冒泡排序
冒泡排序 一. 定义二.题目三. 思路分析(图文结合)四. 代码演示 一. 定义 冒泡排序(Bubble Sort,台湾译为:泡沫排序或气泡排序)是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元…...
Nacos AP架构集群搭建(Windows)
手写SpringCloud项目地址,求个star github:https://github.com/huangjianguo2000/spring-cloud-lightweight gitee:https://gitee.com/huangjianguo2000/spring-cloud-lightweigh 目录: 一:初始化MySQL 二:复制粘贴三份Nacos文…...

nodejs+vue+elementui,图书评论管理系统_g9e3a
用户的功能主要是对首页、图书信息、公告信息、在线咨询、个人中心等进行操作。表名:token语言 node.js 框架:Express 前端:Vue.js 数据库:mysql 数据库工具:Navicat 开发软件:VScode 前端nodejsvueelementui, 管理员…...
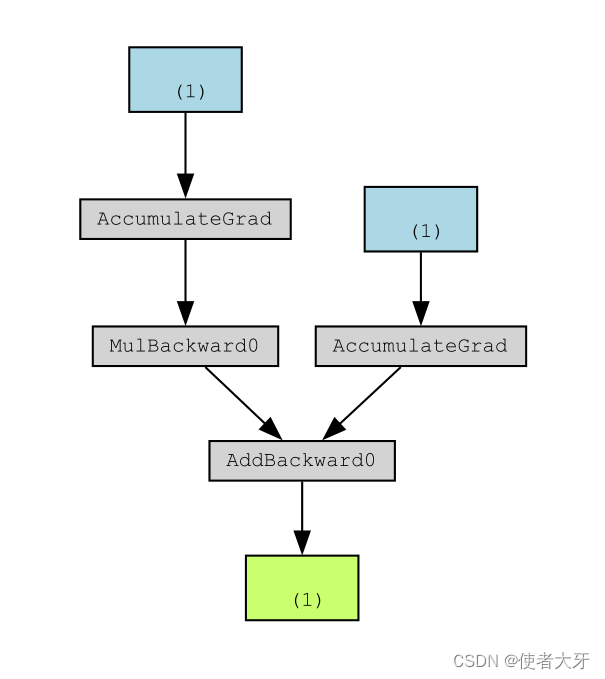
基于TorchViz详解计算图(附代码)
文章目录 0. 前言1. 计算图是什么?2. TorchViz的安装3. 计算图详解 0. 前言 按照国际惯例,首先声明:本文只是我自己学习的理解,虽然参考了他人的宝贵见解,但是内容可能存在不准确的地方。如果发现文中错误,…...

解决GitHub的速度很慢的几种方式
1. GitHub 镜像访问 这里提供两个最常用的镜像地址: https://hub.njuu.cf/search https://www.gitclone.com/gogs/search/clonesearch 也就是说上面的镜像就是一个克隆版的 GitHub,你可以访问上面的镜像网站,网站的内容跟 GitHub 是完整同步…...
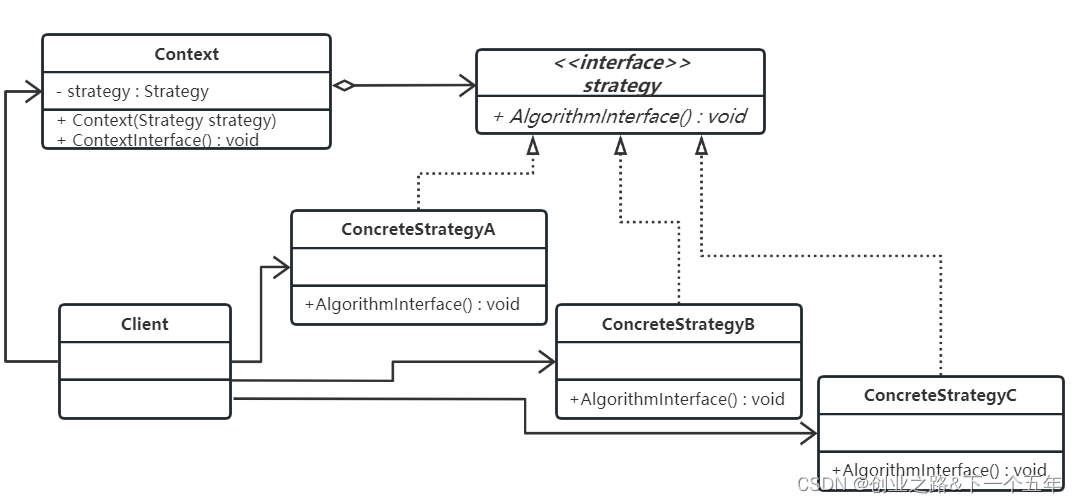
设计模式再探——策略模式
目录 一、背景介绍二、思路&方案三、过程1.策略模式简介2.策略模式的类图3.策略模式代码4.策略模式还可以优化的地方5.策略模式的例子改造(配置文件反射) 四、总结五、升华 一、背景介绍 最近在做产品的过程中,对于主题讨论回复内容,按照追评次数排…...
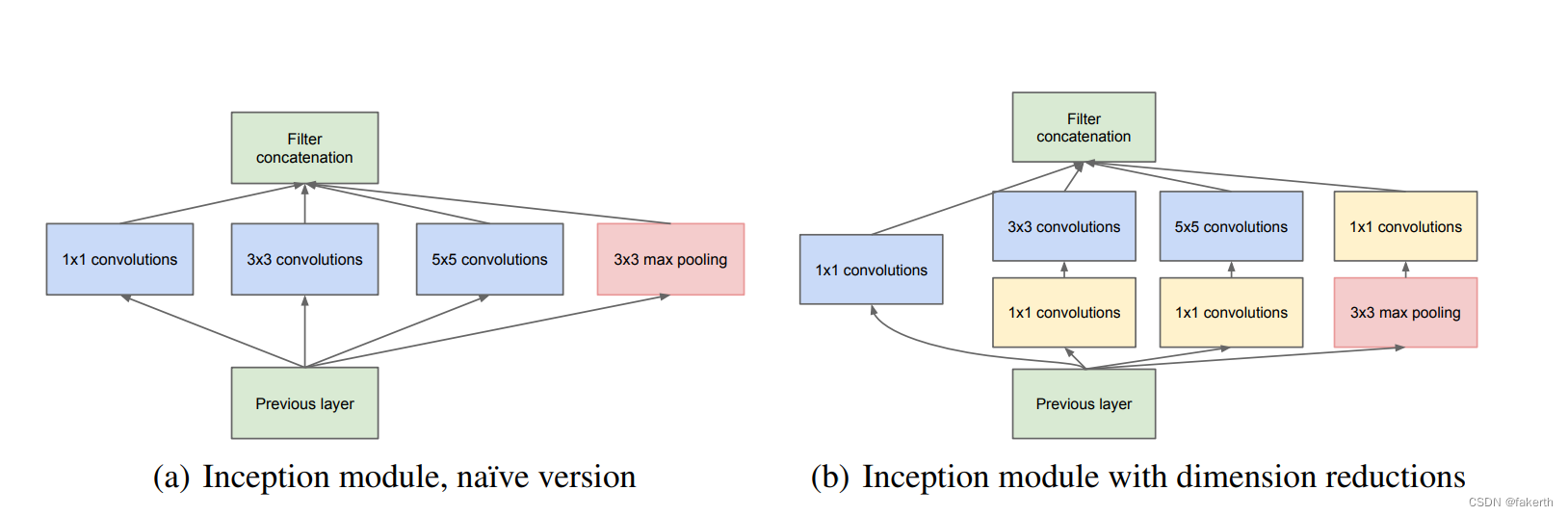
基于Googlenet深度学习网络的人员行为动作识别matlab仿真
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 1. 原理 1.1 深度学习与卷积神经网络(CNN) 1.2 GoogLeNet 2. 实现过程 2.1 数据预处理 2.2 构建网络模型 2.3 数据输入与训练 2.4 模型评估与调优 3. 应用领域…...

存储过程的学习
1,前言 这是实习期间学习的,我可能是在学校没好好听课,(或者就是学校比较垃,没教这部分,在公司经理让我下去自己学习,太难了,因为是公司代码很多部分都是很多表的操作&#…...

zookeeperAPI操作与写数据原理
要执行API操作需要在idea中创建maven项目 (改成自己的阿里仓库)导入特定依赖 添加日志文件 上边操作做成后就可以进行一些API的实现了 目录 导入maven依赖: 创建日志文件: 创建API客户端: (1)…...

防火墙对双通道协议的处理
防火墙是一种网络安全设备或软件,用于控制网络流量并保护计算机网络免受未经授权的访问、恶意攻击和网络威胁。它作为网络的第一道防线,用于监视、过滤和管理进出网络的数据包。 防火墙可以基于预设的安全策略对网络流量进行评估和筛选。它通过比较数据…...
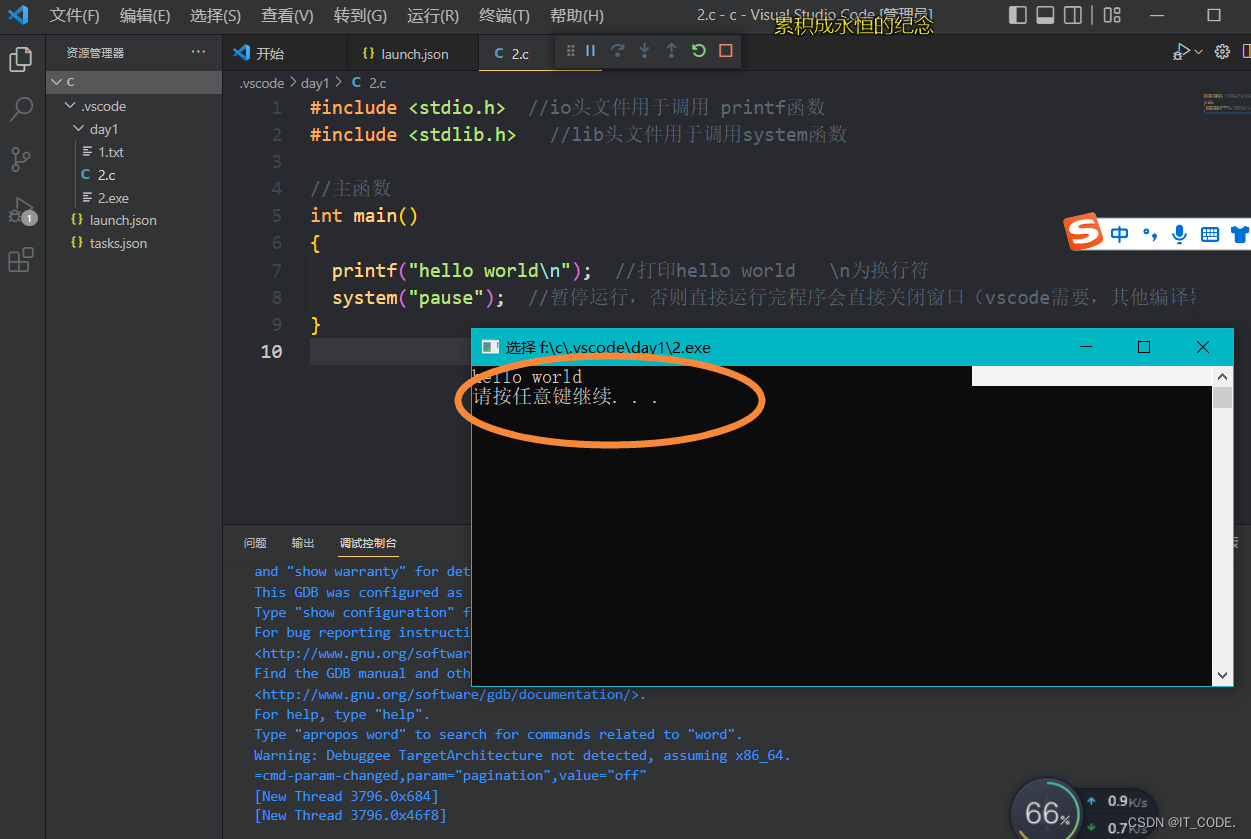
vscode搭建c语言环境问题
c语言环境搭建参考文章:【C语言初级阶段学习1】使用vscode运行C语言,vscode配置环境超详细过程(包括安装vscode和MinGW-W64安装及后续配置使用的详细过程,vscode用户代码片段的使用)[考研专用]_QAQshift的博客-CSDN博客 问题如下:…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...
