当前位置：首页 > news >正文

n-皇后问题

news 2026/2/11 1:55:54

希望这篇题解对你有用，麻烦动动手指点个赞或关注，感谢您的关注

不清楚蓝桥杯考什么的点点下方👇

考点秘籍

想背纯享模版的伙伴们点点下方👇

想背注释模版的伙伴们点点下方👇

往期精彩回顾

想看JavaB组填空题的伙伴们点点下方 👇

竞赛干货

题目

关于n皇后正对角线和反对角线的详细解释

即为什么是dg[x+i]、udg[x-i+n]?
是通过数组下标去维护正反对角线。
通过相同的数组下标保证遍历正反对角线上的点。
(1)x + i实际上是对应的行号加上列号
在这里插入图片描述

注：如图,通过行号加列号,保证了正对角线每个数组下标都一致相同。
所以在判断的时候只需要设置为dg[x+i]即可访问该正对角线上的所有点。

(2)x - i实际上是对应的行号减去列号
会出现负数情况，需要再加上一个n。
即 x-i+n
在这里插入图片描述

注：如图，通过行号减去列号，保证了反对角线上每个数组下标一致(虽然还存在部分的负数)
负数的处理很好办,再加上n,即可将负数保证为正数,这样就不会出现数组下标越界的问题。
所以在判断的时候只需要设置为**udg[x-i+n]**即可访问该反对角线上的所有点。

原理(解析几何)

对于y=k*x+b直线方程
给定一个斜率k和截距b我们可以唯一确定这一条直线
在这里插入图片描述

注：左为正对角线dg[],右为反对角线udg[]。

有了上述的几何基础,我们可以代入到本题中。
在这里插入图片描述

说明：途图中的y为行号(x) , x为列号(i)。
注：找到一个如图的b值,结合直线的斜率便可以唯一确定这一条直线。
对于这条直线上所有的点截距均为b
所有我们只需要找到截距，便可以遍历该对角线上的所有点。

N定义为20的原因

x+i=9+9=18,为防止边界多开一些空间定义为20个单位。

Accode

import java.util.*;
public class Main{static int N=20;static char g[][]=new char [N][N];static boolean dg[]=new boolean[N];static boolean udg[]=new boolean[N];static boolean col[]=new boolean[N];static int n;public static void main(String []args){Scanner in = new Scanner(System.in);n=in.nextInt();for(int i=0;i<n;i++){for(int j=0;j<n;j++){g[i][j]='.';}}dfs(0);}public static void dfs(int x){if(x==n){for(int i=0;i<n;i++){for(int j=0;j<n;j++){System.out.print(g[i][j]);}System.out.println();}System.out.println();return;}//因为我们是去看每一行的位置是否满足，每一行去dfs保证每一行至多只有一个皇后//所以在标记判断的时候，标记上列和正对角线和反对角线即可for(int i=0;i<n;i++){if(!col[i]&&!dg[x+i]&&!udg[x-i+n]){g[x][i]='Q';col[i]=dg[x+i]=udg[x-i+n]=true;dfs(x+1);col[i]=dg[x+i]=udg[x-i+n]=false;g[x][i]='.';//不满足的标为 .}}
}
}

n-皇后问题

希望这篇题解对你有用，麻烦动动手指点个赞或关注，感谢您的关注不清楚蓝桥杯考什么的点点下方👇 考点秘籍想背纯享模版的伙伴们点点下方👇 蓝桥杯省一你一定不能错过的模板大全(第一期) 蓝桥杯省一你一定不能错过的模板大全…...

编程日记 2023/8/14 9:39:21

常见的办法有 1、push()方法 var arr [a, b, c,d]; arr.push(e); console.log(arr); // [a, b, c, d,e] 2、concat()方法 var arr1 [a, b, c]; var arr2 [d, e, f]; var arr3 arr1.concat(arr2); console.log(arr3); // [a, b, c, d, e, f] 3、可以使用ES6中的spread操作符…...

编程日记 2023/8/14 9:38:19

串口通信收发项目级一

void 定时器中断函数入口(void) { if(判断是否为定时器中断) { static uint16_t num定义静态变量; static uint8_t index定义静态变量; unsigned char buff_busy定义局部变量; if(串口中断接收数据数量>静态变量) { 静态变量串口中断接收数据数量; } else if(静态变量串口中…...

编程日记 2023/8/14 9:37:18

设计模式之七：适配器模式与外观模式

面向对象适配器将一个接口转换成另一个接口，以符合客户的期望。 // 用火鸡来冒充一下鸭子class Duck { public:virtual void quack() 0;virtual void fly() 0; };class Turkey { public:virtual void gobble() 0;virtual void fly() 0; };class TurkeyAdapter :…...

编程日记 2023/8/14 9:36:17

FFmpeg接收UDP码流

一、FFmpeg参数初始化： //在打开码流前指定各种参数比如:探测时间/超时时间/最大延时等//设置缓存大小,1080p可将值调大av_dict_set(&options, "buffer_size", "8192000", 0);//以tcp方式打开,如果以udp方式打开将tcp替换为udpav_dict_set(…...

编程日记 2023/8/14 9:35:16

【Pytroch】基于支持向量机算法的数据分类预测（Excel可直接替换数据）

【Pytroch】基于支持向量机算法的数据分类预测（Excel可直接替换数据） 1.模型原理2.数学公式3.文件结构4.Excel数据5.下载地址6.完整代码7.运行结果 1.模型原理支持向量机（Support Vector Machine，SVM）是一种强大的监…...

编程日记 2023/8/14 9:34:13

【Git】git初始化项目时 | git默认创建main分之 | 如何将git默认分支从main改为master

git 更改 branch 在 Git 中，如果你在第一次提交后想要将默认分支名从 main 修改为 master，你可以按照以下步骤进行操作： 创建 master 分支： 首先，你需要在当前的 main 分支基础上创建一个新的 master 分支。使用以下命…...

编程日记 2023/8/14 9:33:11

Vue3中配置environment

environment顾名思义就是环境，对于项目来说，无非就是： 开发环境：development生产环境：production 某些逻辑，配置等在两个不同的环境中要呈现出不同的状态，所以environment是一个必要的事情。 …...

编程日记 2023/8/14 9:32:08

前端基础积累_新技术_Vue_React_H5_奇怪的BUG_面试_招聘

前端之路序前几天在博客园收到了一封来自出版社的消息，说看到原来很久之前写的 < VueJS 源码分析的文章 > 希望能够联系他们出版社去写书。这样的事情虽然在博客园是会经常发生的，但是这也让我意识到了，多多写高质量的文章能够给 co…...

编程日记 2023/8/14 9:31:07

【密码学】维京密码

维京密码瑞典罗特布鲁纳巨石上的图案看起来毫无意义，但是它确实是一种维京密码。如果我们注意到每组图案中长笔画和短笔画的数量，将得到一组数字2、4、2、3、3、5、2、3、3、6、3、5。组合配对得到24、23、35、23、36、35。现在考虑如图1.4所示的内容&a…...

编程日记 2023/8/14 9:30:06

小米基于 Flink 的实时计算资源治理实践

摘要：本文整理自小米高级软件工程师张蛟，在 Flink Forward Asia 2022 生产实践专场的分享。本篇内容主要分为四个部分： 发展现状与规模框架层治理实践平台层治理实践未来规划与展望点击查看原文视频 & 演讲PPT 一、发展现状与规模如上图…...

编程日记 2023/8/14 9:29:05

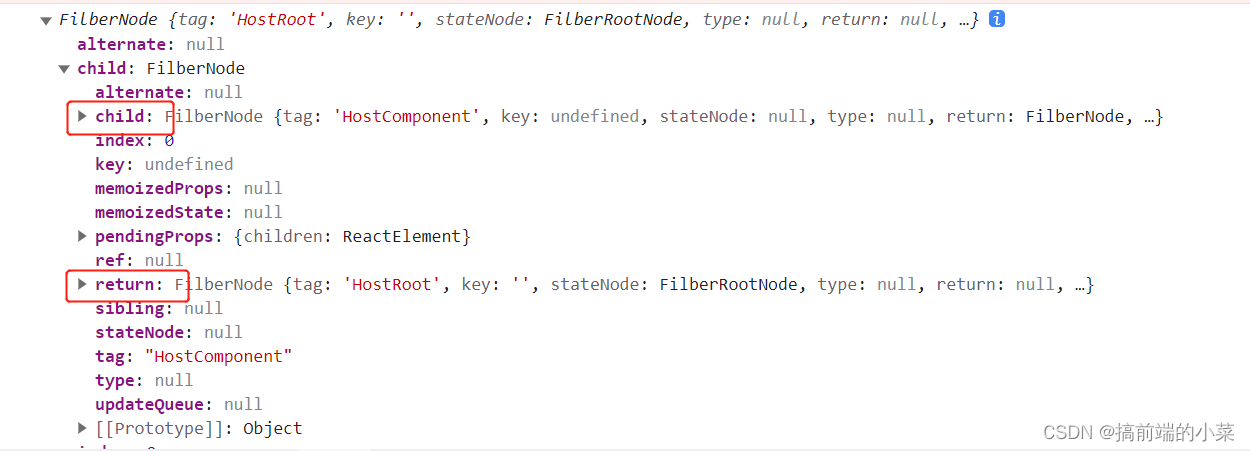
React源码解析18（3）------ beginWork的工作流程【mount】

摘要 OK，经过上一篇文章。我们调用了： const root document.querySelector(#root); ReactDOM.createRoot(root)生成了FilberRootNode和HostRootFilber。并且二者之间的对应关系也已经确定。而下一步我们就需要调用render方法来讲react元素挂载在ro…...

编程日记 2023/8/14 9:28:03

JAVA SpringBoot 项目多线程、线程池的使用。

1.1 线程： 线程就是进程中的单个顺序控制流，也可以理解成是一条执行路径单线程：一个进程中包含一个顺序控制流（一条执行路径） 多线程：一个进程中包含多个顺序控制流（多条执行路径&#xff0…...

编程日记 2023/8/14 9:27:02

【数据结构与算法】动态规划算法

动态规划算法应用场景 - 背包问题背包问题：有一个背包，容量为 4 磅，现有如下物品： 物品重量价格吉他（G）11500音响（S）43000电脑（L）32000 要求达到的目标…...

编程日记 2023/8/14 9:26:01

离线安装vscode插件，导出 Visual Studio Code 的扩展应用，并离线安装

在没有网络的情况下，如何安装vscode插件 1.使用之前电脑安装过的插件包 Visual Studio Code 的扩展应用安装位置在文件夹 .vscode/extensions 下。不同平台，它位于： Windows %USERPROFILE%\.vscode\extensions Mac ~/.vscode/extensions L…...

编程日记 2023/8/14 9:24:59

【ChatGPT 指令大全】怎么使用ChatGPT辅助程式开发

目录写程式解读程式码重构程式码解 bug 写测试写 Regex 总结在当今快节奏的数字化世界中，程式开发变得越来越重要和普遍。无论是开发应用程序、网站还是其他软件，程式开发的需求都在不断增长。然而，有时候我们可能会遇到各种问题…...

编程日记 2023/8/14 9:23:58

涂色

蜀山区2021年信息学竞赛试题题目描述 Description 小李喜欢写日记，为了有效区分每题记录的内容，他循环使用七种不同颜色的笔在日记本上记录每天发生的事情，循环次序分别为Red,Orange,Yellow,Green,Blue,Cyan,Purple,由于近期工作繁忙&…...

编程日记 2023/8/14 9:22:56

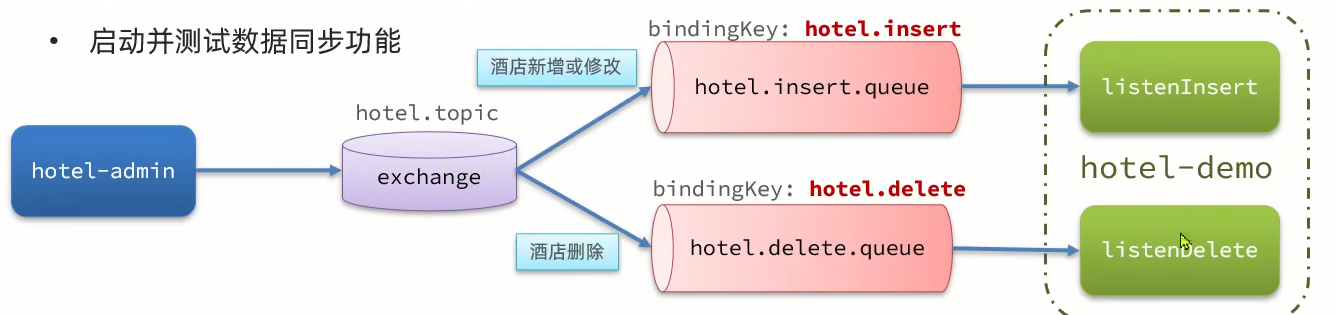
微服务——数据同步

问题分析 mysql和redis之间有数据同步问题，ES和mysql之间也有数据同步问题。单体项目可以在crud时就直接去修改，但在微服务里面不同的服务不行。方案一方案二方案三总结导入酒店管理项目倒入完成功启动后可以看见数据成功获取到了声明队列和…...

编程日记 2023/8/14 9:21:55

MySQL 手机选号(AABB、ABCD、DCBA、AAA)，SQL SERVER 手机选号(AABB、ABCD、DCBA、AAA)，通过规则查询靓号

先上SQL SERVER： create table plat_uidlist(Uidd varchar(15) , Areaid int , State int)insert into plat_uidlist values(2335435 ,8 ,0 ) insert into plat_uidlist values(2335436 ,8 ,1 ) insert into plat_uidlist values(2335437 ,2 ,2 ) insert into plat…...

编程日记 2023/8/14 9:20:54

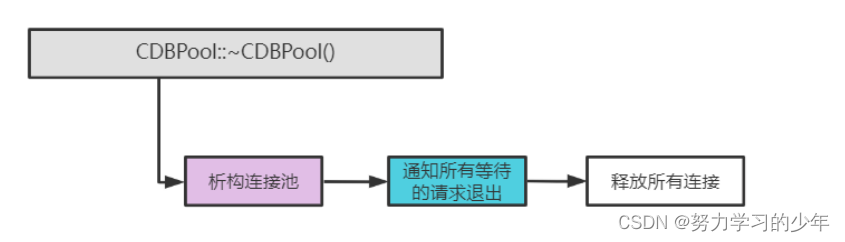
【server组件】——mysql连接池的实现原理

目录 1.池化技术 2.数据库连接池的定义 3.为什么要使用连接池 4. 数据库连接池的运行机制 5. 连接池与线程池的关系 6. CResultSet的设计 6.1构造函数 7. CDBConn的设计 6.1.构造函数 6.2.init——初始化连接 8.数据库连接池的设计要点 9.接口设计 9.1 构造函数 …...

编程日记 2023/8/14 9:19:53

椭圆曲线密码学(ECC)

一、ECC算法概述椭圆曲线密码学（Elliptic Curve Cryptography）是基于椭圆曲线数学理论的公钥密码系统，由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA，ECC在相同安全强度下密钥更短（256位ECC ≈ 3072位RSA…...

编程新知 2025/10/1 22:26:06

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力

引言： 在人工智能快速发展的浪潮中，快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型（LLM）。该模型代表着该领域的重大突破，通过独特方式融合思考与非思考…...

编程新知 2026/2/6 19:29:20

第一篇：Agent2Agent (A2A) 协议——协作式人工智能的黎明

AI 领域的快速发展正在催生一个新时代，智能代理（agents）不再是孤立的个体，而是能够像一个数字团队一样协作。然而，当前 AI 生态系统的碎片化阻碍了这一愿景的实现，导致了“AI 巴别塔问题”——不同代理之间…...

编程新知 2026/1/31 3:30:33

RNN避坑指南：从数学推导到LSTM/GRU工业级部署实战流程

本文较长，建议点赞收藏，以免遗失。更多AI大模型应用开发学习视频及资料，尽在聚客AI学院。本文全面剖析RNN核心原理，深入讲解梯度消失/爆炸问题，并通过LSTM/GRU结构实现解决方案，提供时间序列预测和文本生成…...

编程新知 2026/1/20 17:16:46

现有的 Redis 分布式锁库（如 Redisson）提供了哪些便利？

现有的 Redis 分布式锁库（如 Redisson）相比于开发者自己基于 Redis 命令（如 SETNX, EXPIRE, DEL）手动实现分布式锁，提供了巨大的便利性和健壮性。主要体现在以下几个方面： 原子性保证 (Atomicity)&#xff…...

编程新知 2025/9/23 11:26:04

基于IDIG-GAN的小样本电机轴承故障诊断

目录 🔍 核心问题一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化（Gradient Normalization） (2) 判别器梯度间隙正则化（Discriminator Gradient Gap Regularization） (3) 自注意力机制（Self-Attention） 3. 完整损失函数二…...

编程新知 2026/1/31 10:58:46

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能

1. 开发环境准备安装DevEco Studio 3.1： 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置： // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

编程新知 2025/12/29 15:43:26