【数学建模】--聚类模型
聚类模型的定义:
“物以类聚,人以群分”,所谓的聚类,就是将样本划分为由类似的对象组成的多个类的过程。聚类后,我们可以更加准确的在每个类中单独使用统计模型进行估计,分析或预测;也可以探究不同类之间的相关性和主要差异。
聚类和分类的区别:分类是已知类别的,聚类未知。
K-means聚类算法
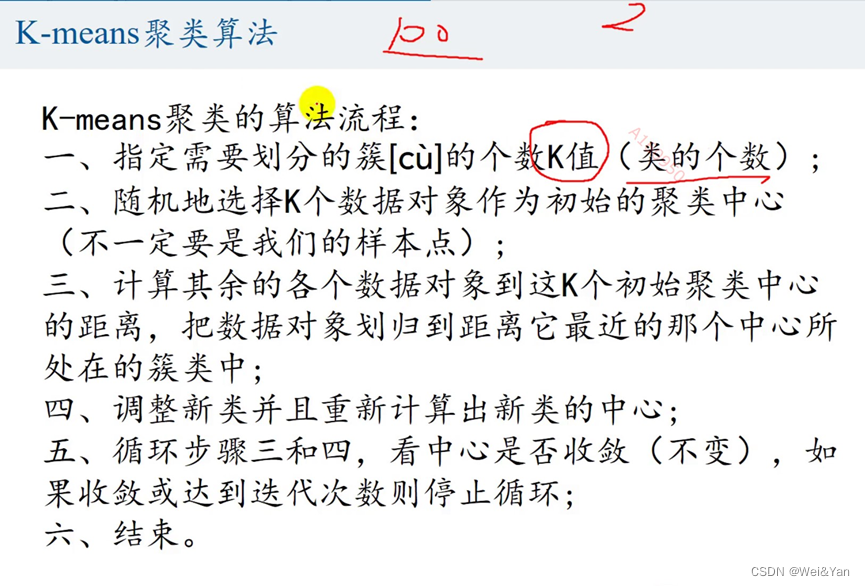
流程:
- 指定划分的簇的k值(类的个数)
- 随机选择k个数据作为哦初始聚类中心(不一定是样本点)
- 将其余数据划分到距离较近的聚类中心
- 调整新类,将中心更新为已划分数据的中心
- 重复3,4步检查中心是否收敛(不变),如果收敛或达到迭代次数使停止循环。(一般循迭代次数设置为10次)
- 结束。
图形结合理解: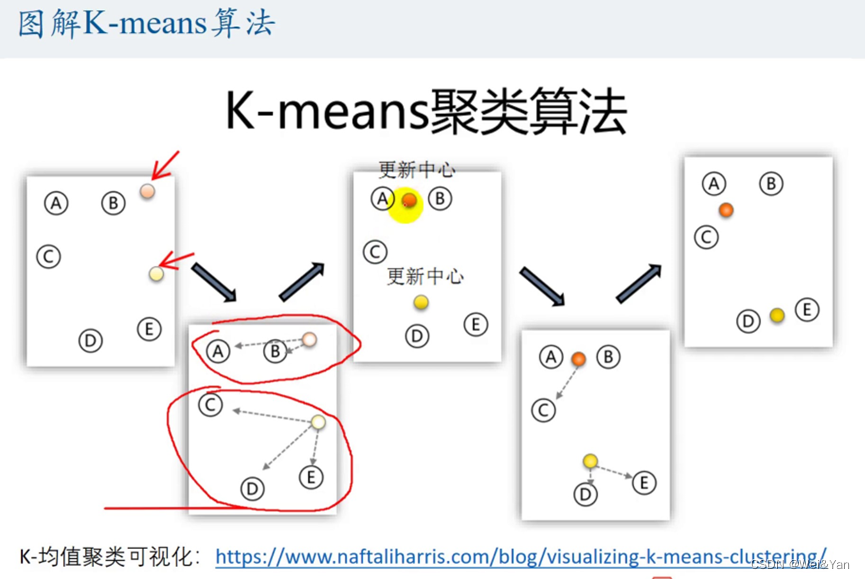
我们可以登录网站自行体验:Visualizing K-Means Clustering
如果使自己添加类的位置可以选择I‘ll Choose
选择自己喜欢的图形:
选择图形后添加类的位置然后一直点GO/Update Centroids直至不想不再发生变化。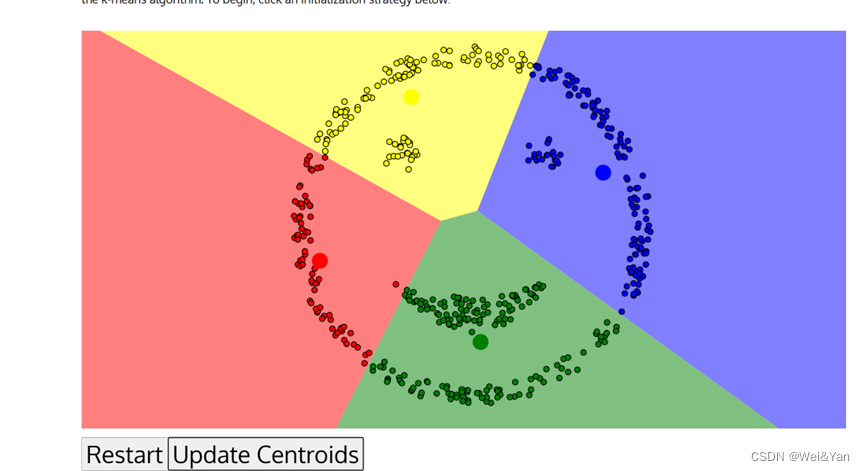
算法流程图: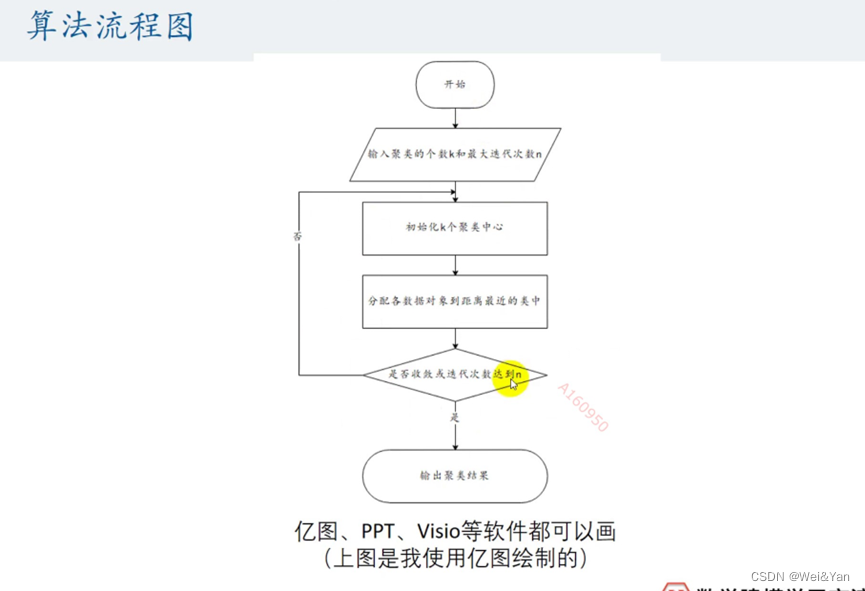
K_means算法的评价:
优点:快,高效率
缺点:需要给出k;对聚类中心敏感,聚类中心的位置不同结果不同;对孤立点敏感,孤立点对中心和其余样本带点的更新影响较大。
K-means算法—Spss操作: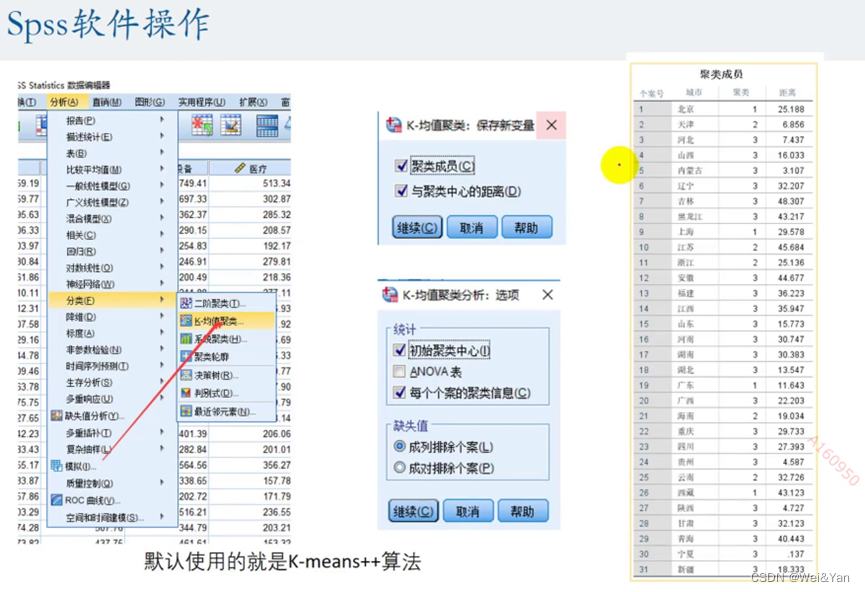
聚类数根据自己想要分类的层次决定。
这里我们分为了高消费,中消费,低消费三类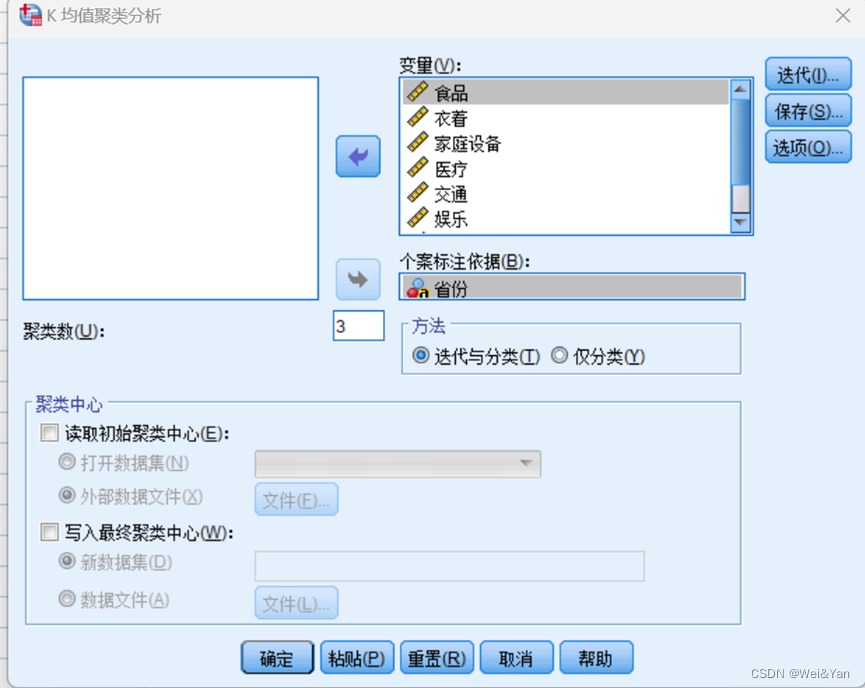
得出结果
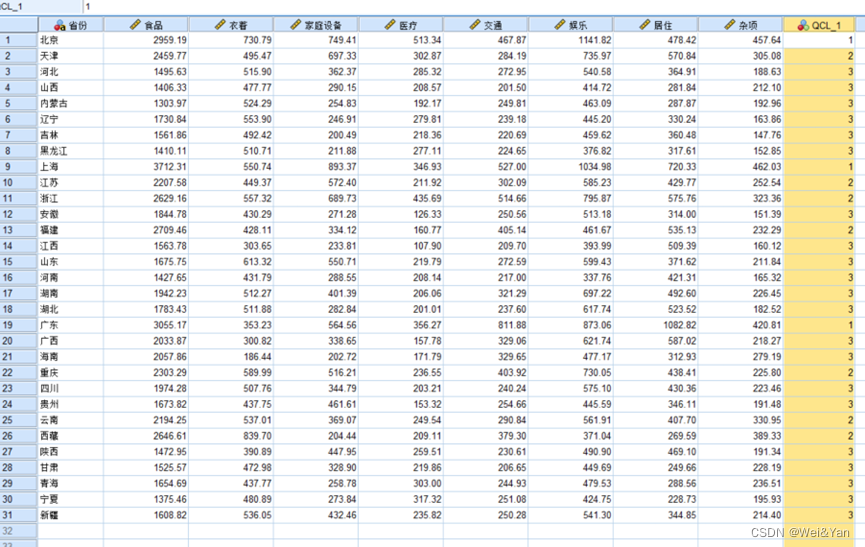
K-means算法的讨论:
需要自己给定k,当变量量纲不同的时候需要去量纲化。
Spss中去量纲化操作:
分析->描述统计->描述->导入需要去量纲化变量->√将标准化值另存为变量。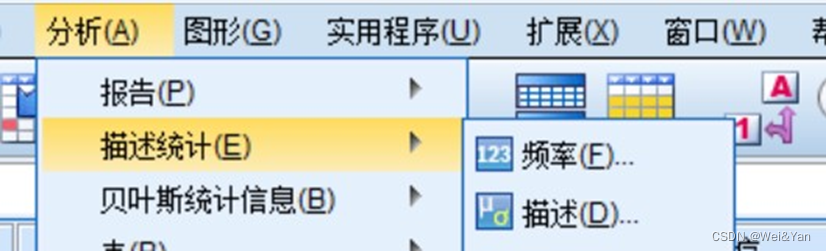

得到去量纲话Z-name
因为本次的例子变量单位相同不需要去量纲化,为了方便就拿此例子的数据去量纲化得到的结果有些轻微差
系统(层次)模型
简介: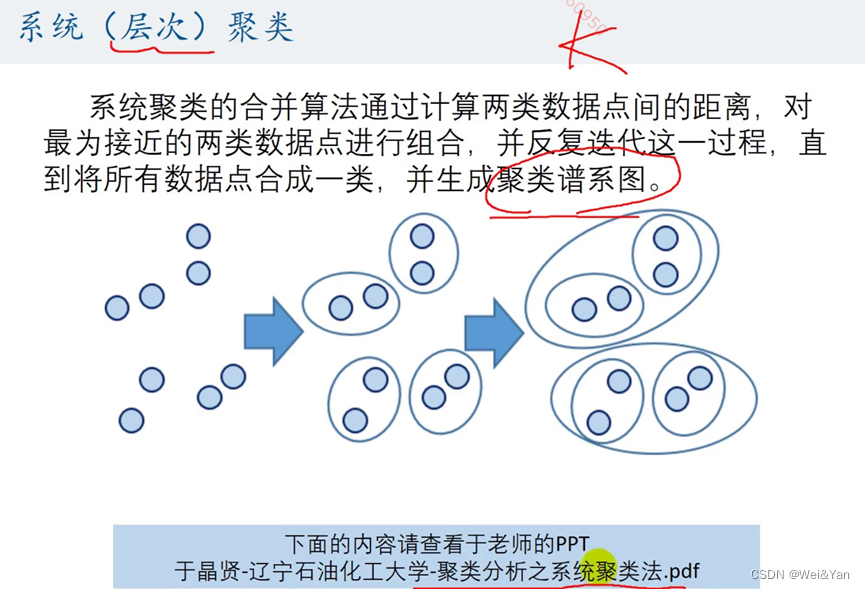
过程及原理简介: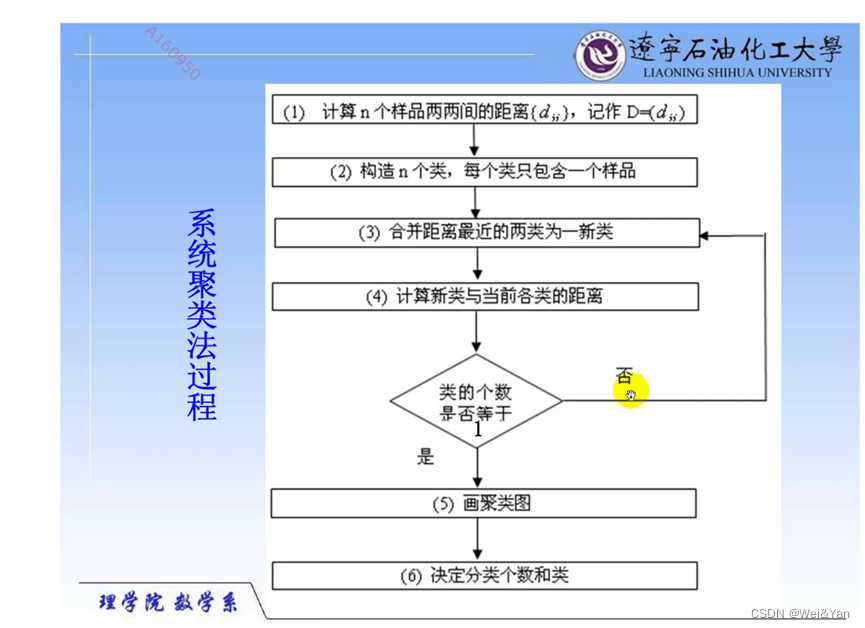
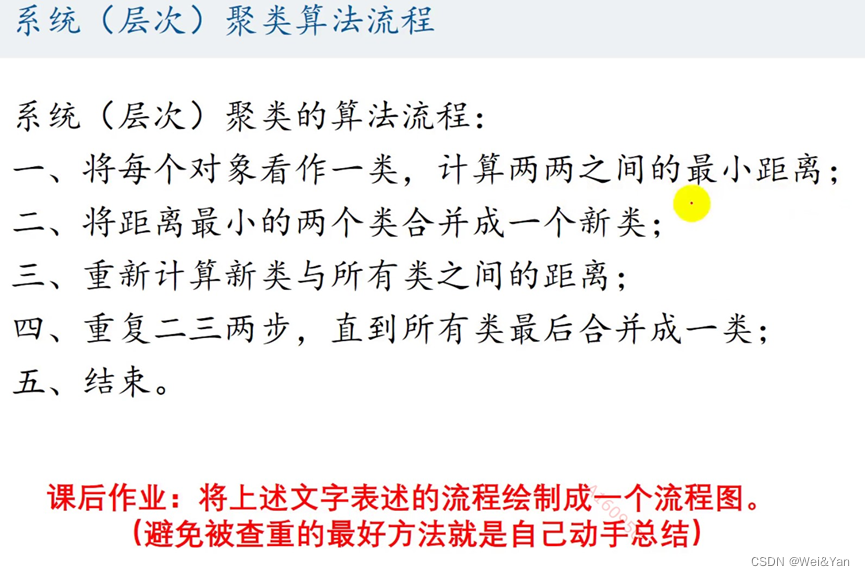
样品与样品之间的常用距离:
指标与指标之间的常用距离:
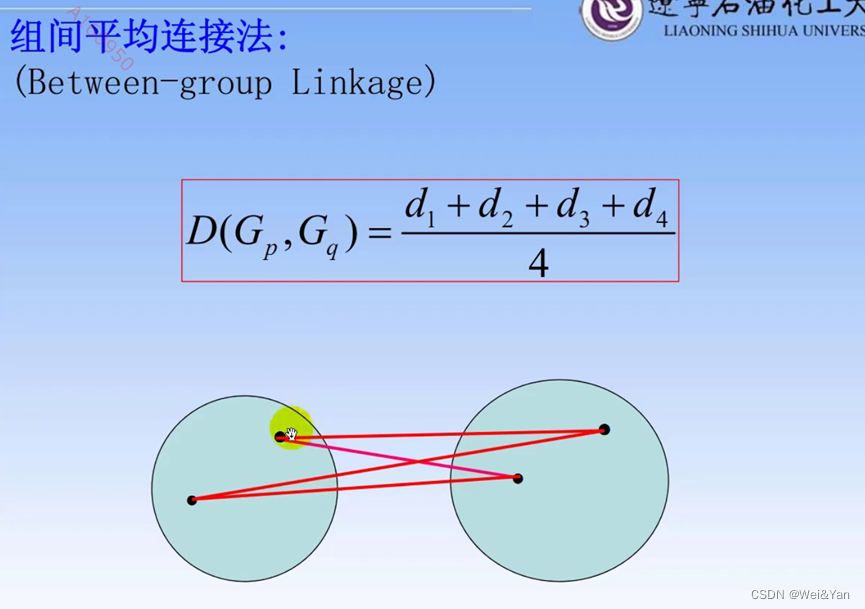
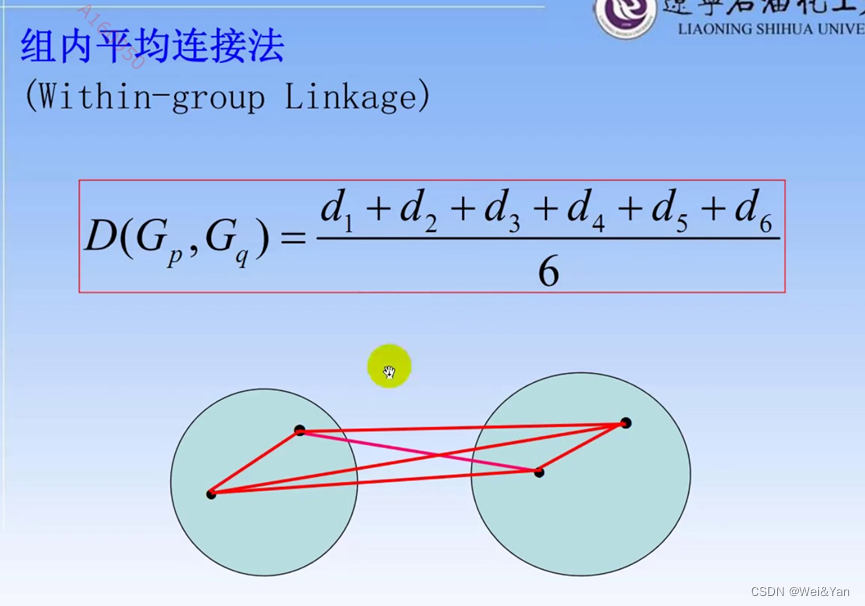
类与类之间的常用距离以及计算方法:

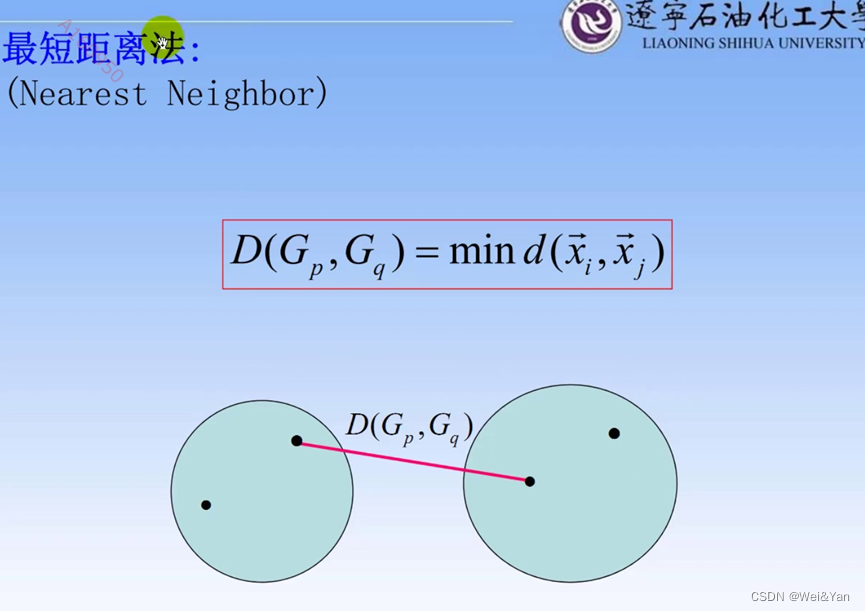
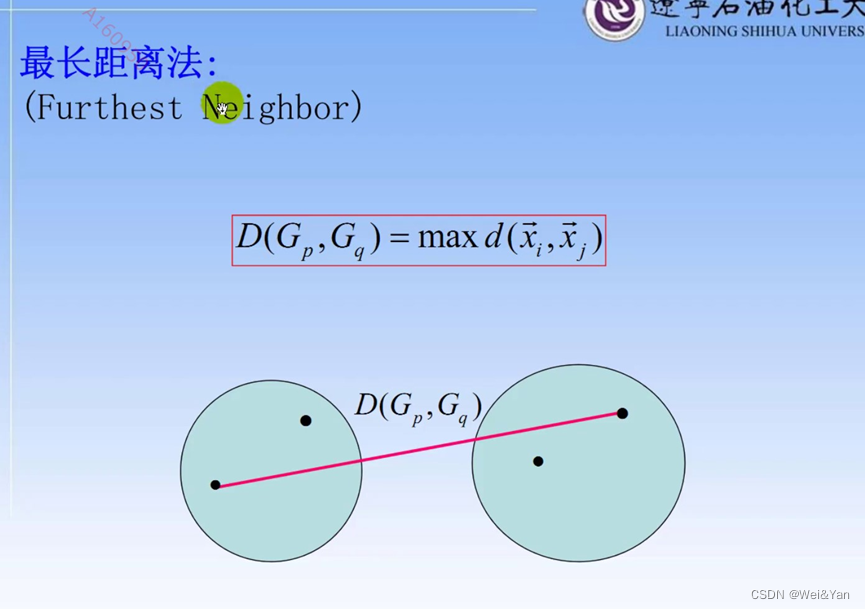
案例: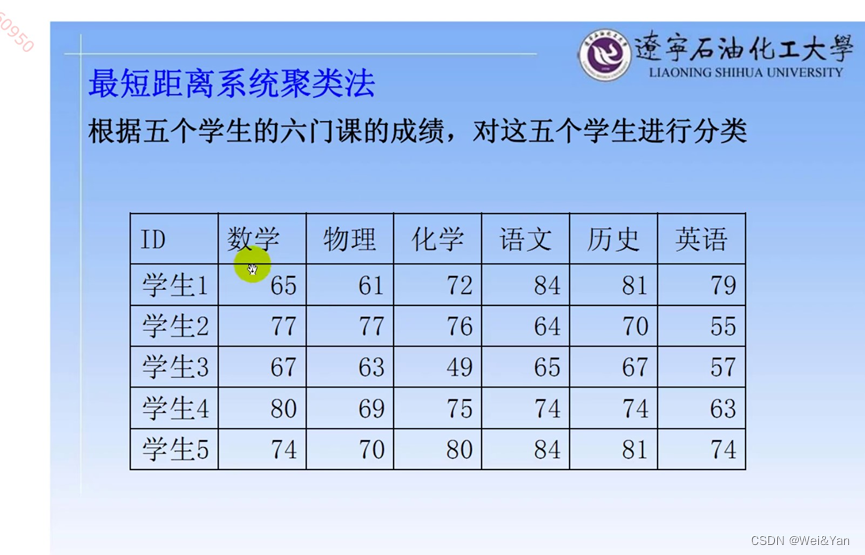
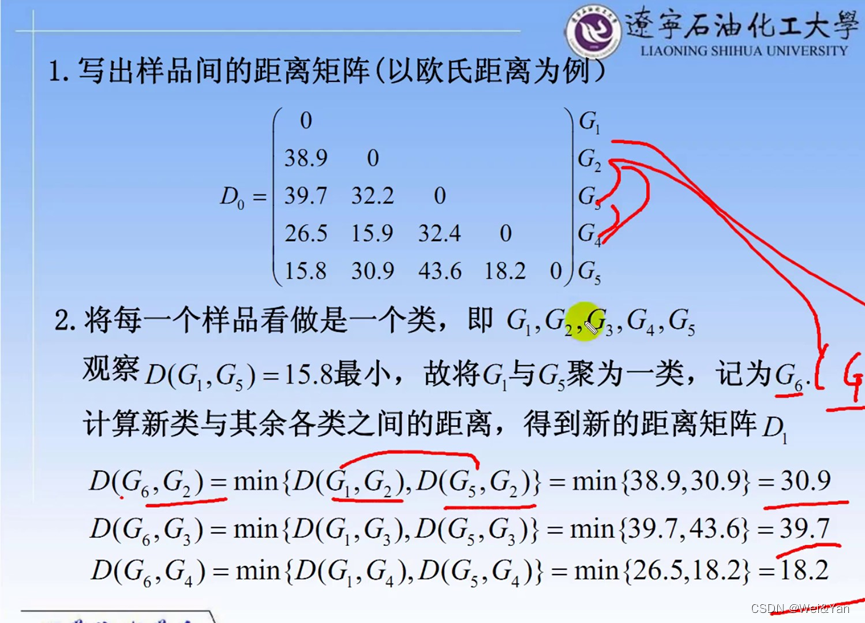
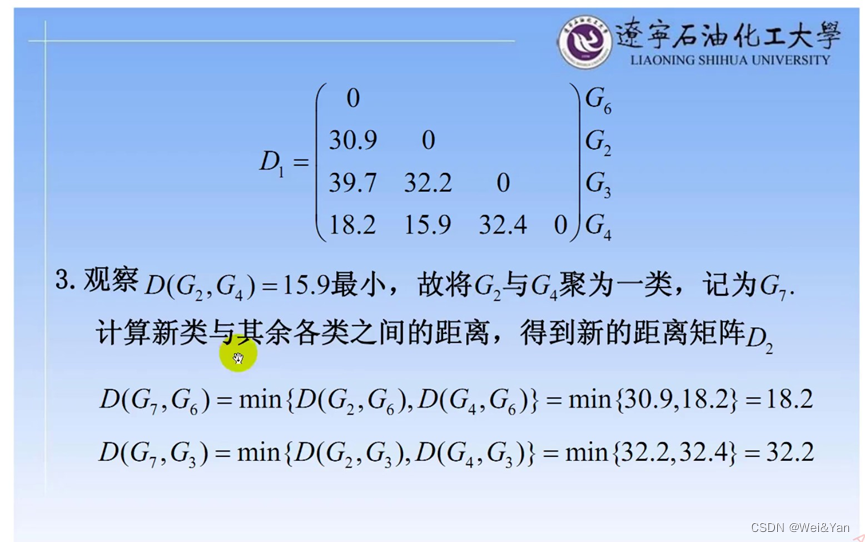
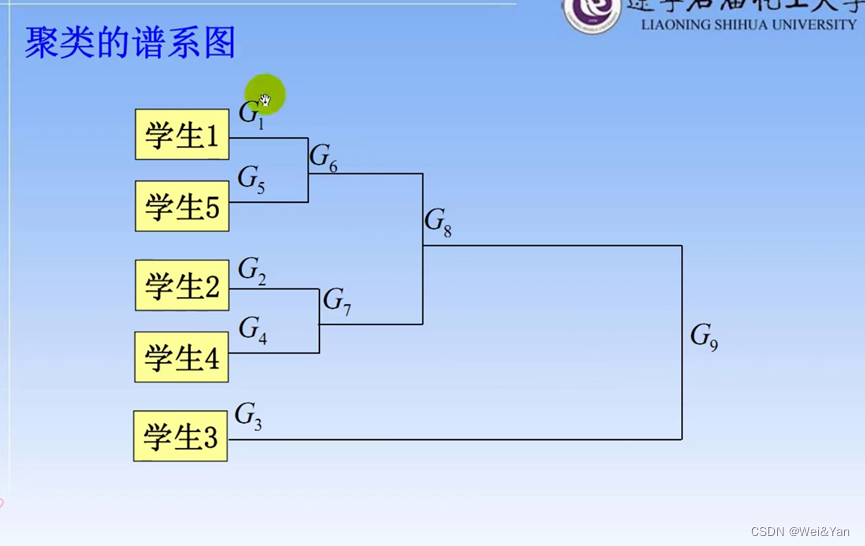
得到聚类的谱系图:
我们想要将数据分成几类通过对谱系图作垂线可得到明显的类组如在G9后面的线作垂线得到G1,2,4,5,6,7,8为一组,G3为一组一共两组。
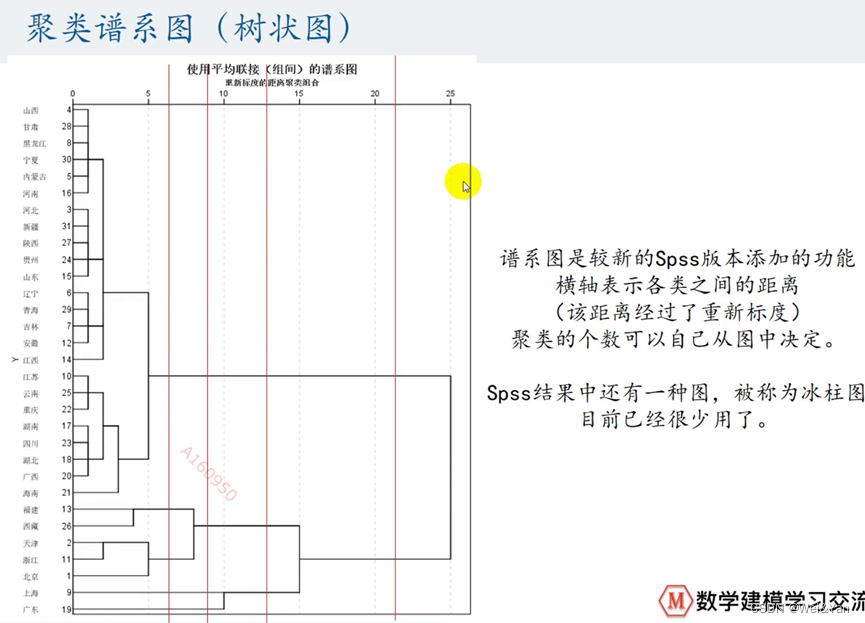
注意问题:

系统聚类在SPSS中的操作:
分析-分类-系统聚类-导入数据-图-√谱系图
由冰柱图聚类谱系图等。
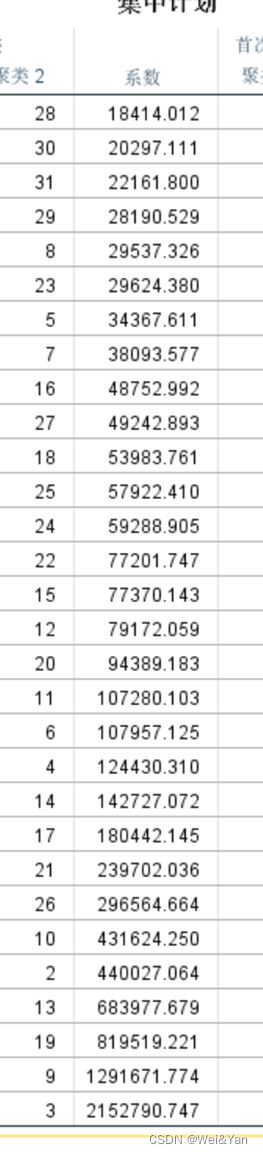
如何确定类的个数:利用Excel中的折线图,在折线趋缓的时候找对应的横坐标即是合适的分类个数。
操作:
1.复制stata中得到的系数-excel-排序-降序
2.插入-推荐的图标-散点图-调整合适的x轴坐标范围
3.观察下降趋势趋缓的地方对应的x可作为分类的个数。
STATA EXCEL
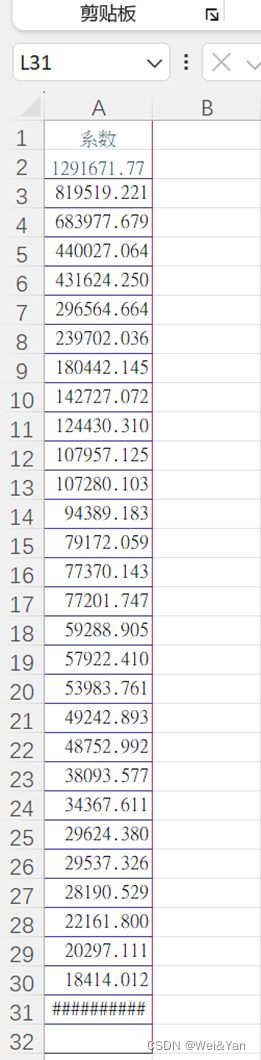
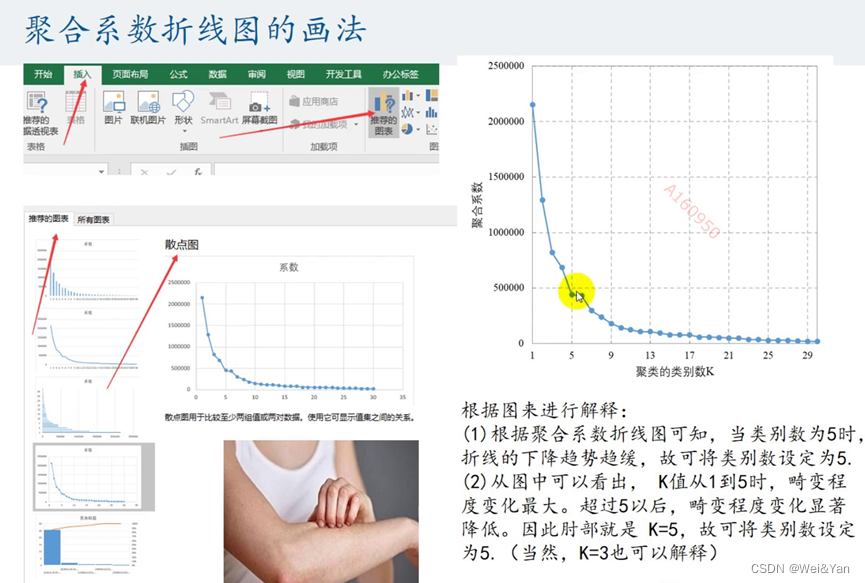
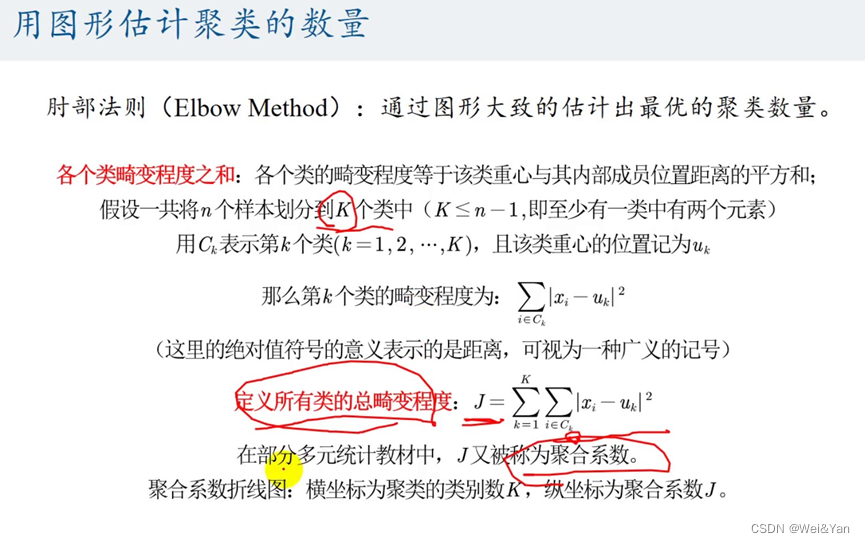
确定K后保存聚类结果并画图
- 通过excel的三点分析确定k
分析-分类-系统聚类-保存-单个解-聚类数
- 作图:
图形-图标构建-散点图/点图-2个指标(第二个)上拖,3个指标(第四个)上拖-输入x轴,y轴-设置颜色(聚类)-组-点id标签(将省份拖入)-修改图的背景,散点等颜色(双击编辑)
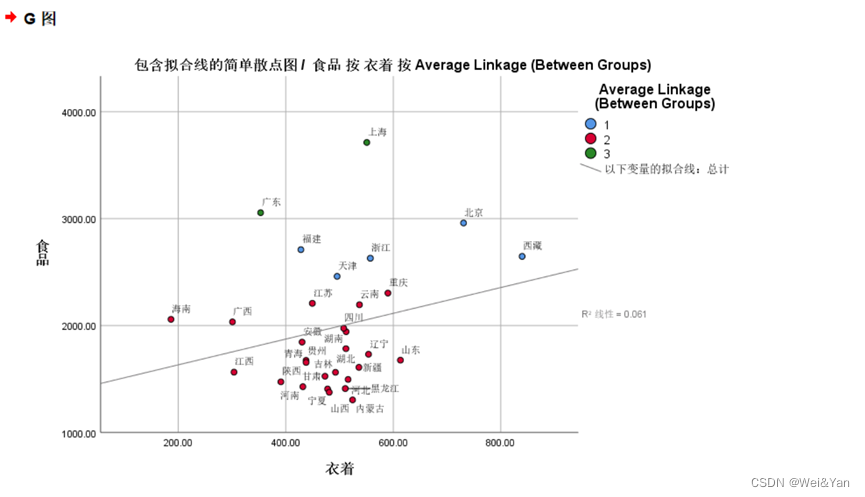
图二是三维的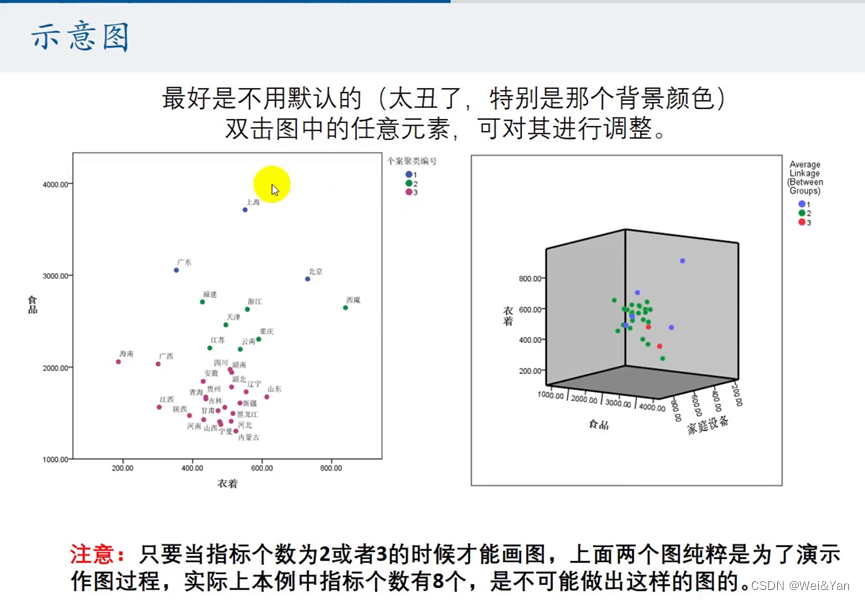
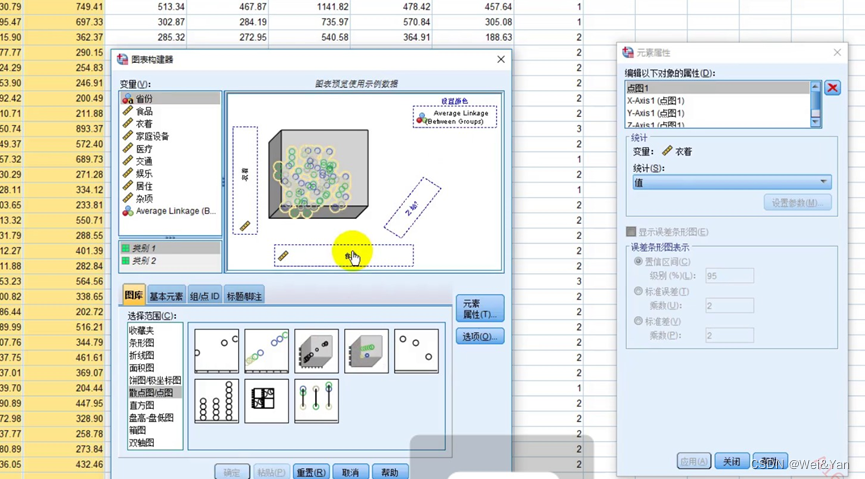
编辑界面:
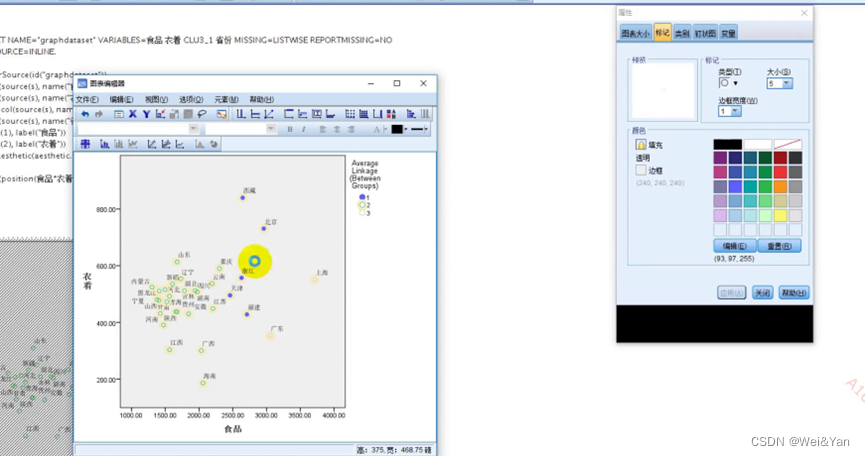
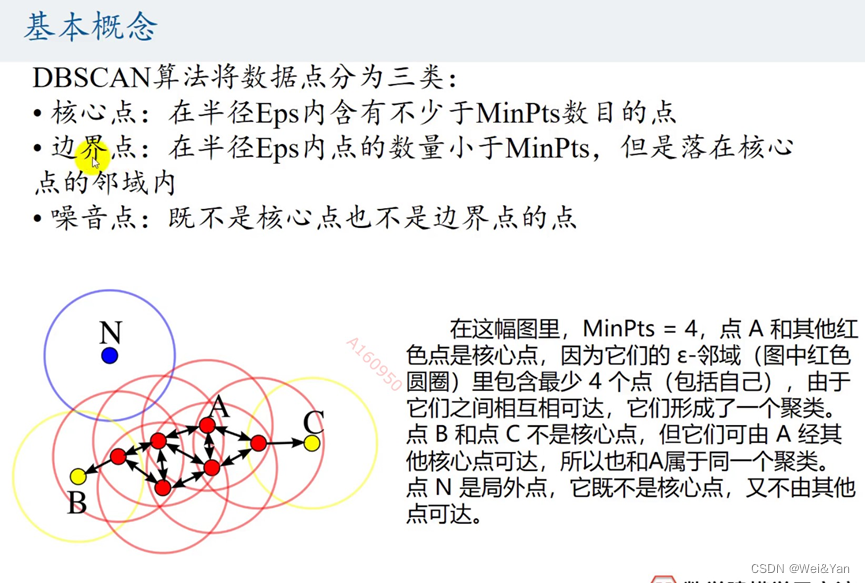
DBSCAN算法
基本概念:
可以理解为流感,按一定的半径不断蔓延传播。
DBSCAN的优缺点:
指标只有很少比如只有两个的时候较为合适,DSCAN的制图对半径,和圆内所能容纳最大聚类个数非常敏感,稍微修改就有很大的显著差异。
DBSACN的制图网站:Visualizing DBSCAN Clustering (naftaliharris.com)
演示:
半径为1.2,最少容纳点为4: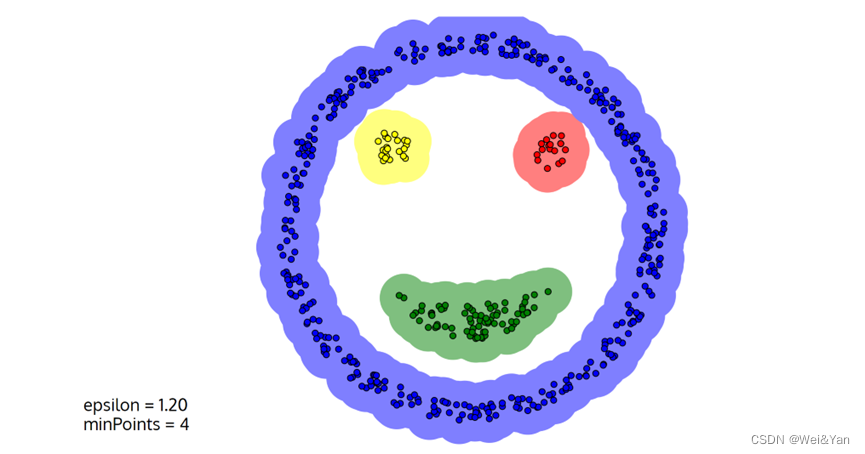
半径为0.8,最少容纳点为4: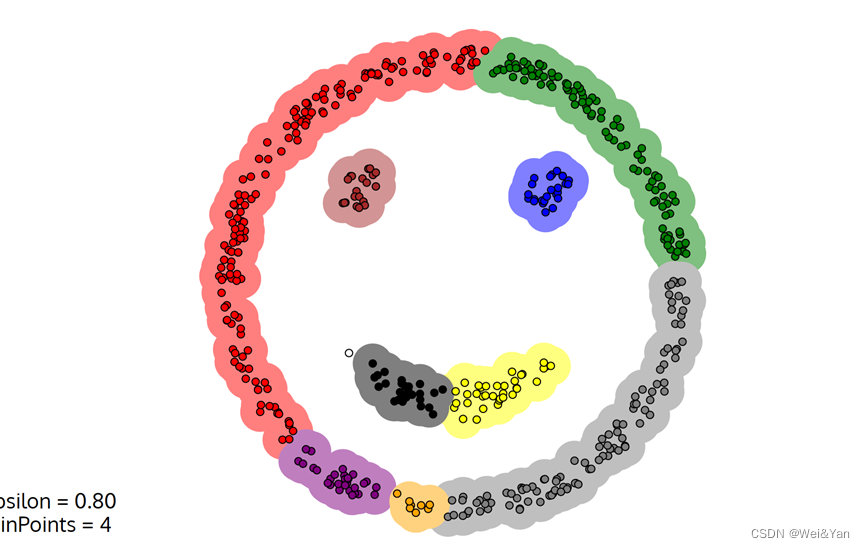
DBSACN的伪代码:
Matlab中的DBSACN代码:
IDX中的数据就是每个数据的分类,为0则是孤立点。
旁边则是DBSACN用matlab画出的图形。
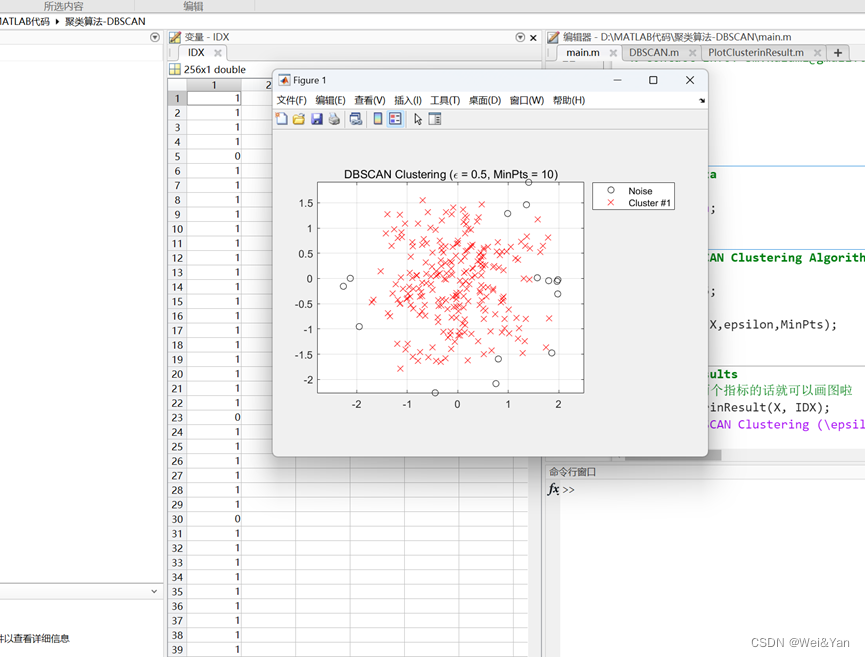
Matlab代码:
主函数:
clc;
clear;
close all;%% Load Dataload mydata;%这里的数据跟随自己需要聚类的数据可以改变,后面的X是博主调试时使用的数据名可以自己改变。%% Run DBSCAN Clustering Algorithmepsilon=0.5;
MinPts=10;
IDX=DBSCAN(X,epsilon,MinPts);%% Plot Results
% 如果只要两个指标的话就可以画图啦
PlotClusterinResult(X, IDX);
title(['DBSCAN Clustering (\epsilon = ' num2str(epsilon) ', MinPts = ' num2str(MinPts) ')']);
DBSCAN函数:
function [IDX, isnoise]=DBSCAN(X,epsilon,MinPts)C=0;n=size(X,1);IDX=zeros(n,1); % 初始化全部为0,即全部为噪音点D=pdist2(X,X);visited=false(n,1);isnoise=false(n,1);for i=1:nif ~visited(i)visited(i)=true;Neighbors=RegionQuery(i);if numel(Neighbors)<MinPts% X(i,:) is NOISEisnoise(i)=true;elseC=C+1;ExpandCluster(i,Neighbors,C);endendendfunction ExpandCluster(i,Neighbors,C)IDX(i)=C;k = 1;while truej = Neighbors(k);if ~visited(j)visited(j)=true;Neighbors2=RegionQuery(j);if numel(Neighbors2)>=MinPtsNeighbors=[Neighbors Neighbors2]; %#okendendif IDX(j)==0IDX(j)=C;endk = k + 1;if k > numel(Neighbors)break;endendendfunction Neighbors=RegionQuery(i)Neighbors=find(D(i,:)<=epsilon);endendDBSCAN制图函数:
function PlotClusterinResult(X, IDX)k=max(IDX);Colors=hsv(k);Legends = {};for i=0:kXi=X(IDX==i,:);if i~=0Style = 'x';MarkerSize = 8;Color = Colors(i,:);Legends{end+1} = ['Cluster #' num2str(i)];elseStyle = 'o';MarkerSize = 6;Color = [0 0 0];if ~isempty(Xi)Legends{end+1} = 'Noise';endendif ~isempty(Xi)plot(Xi(:,1),Xi(:,2),Style,'MarkerSize',MarkerSize,'Color',Color);endhold on;endhold off;axis equal;grid on;legend(Legends);legend('Location', 'NorthEastOutside');end相关文章:

【数学建模】--聚类模型
聚类模型的定义: “物以类聚,人以群分”,所谓的聚类,就是将样本划分为由类似的对象组成的多个类的过程。聚类后,我们可以更加准确的在每个类中单独使用统计模型进行估计,分析或预测;也可以探究不…...

css3新增选择器总结
目录 一、属性选择器 二、结构伪类选择器 三、伪元素选择器 四、UI状态伪类选择器 五、反选伪类选择器 六、target选择器 七、父亲选择器、后代选择器 八、相邻兄弟选择器、兄弟们选择器 一、属性选择器 (除IE6外的大部分浏览器支持) E&#…...

0基础学C#笔记10:归并排序法
文章目录 前言一、递归的方式二、代码总结 前言 将一个大的无序数组有序,我们可以把大的数组分成两个,然后对这两个数组分别进行排序,之后在把这两个数组合并成一个有序的数组。由于两个小的数组都是有序的,所以在合并的时候是很…...

nlohmann json:通过for遍历object和array
object和array可以使用数for进行遍历: #include <iostream> #include <nlohmann/json.hpp> using namespace std; using json = nlohmann::json;auto checkJsonType(json& x) {if(x.type() == json::value_t::null){cout<<x<<" is null&quo…...

适配器模式:将不兼容的接口转换为可兼容的接口
适配器模式:将不兼容的接口转换为可兼容的接口 什么是适配器模式? 适配器模式是一种结构型设计模式,用于将一个类的接口转换为客户端所期望的另一个接口。它允许不兼容的类能够合作,使得原本由于接口不匹配而无法工作的类能够一…...
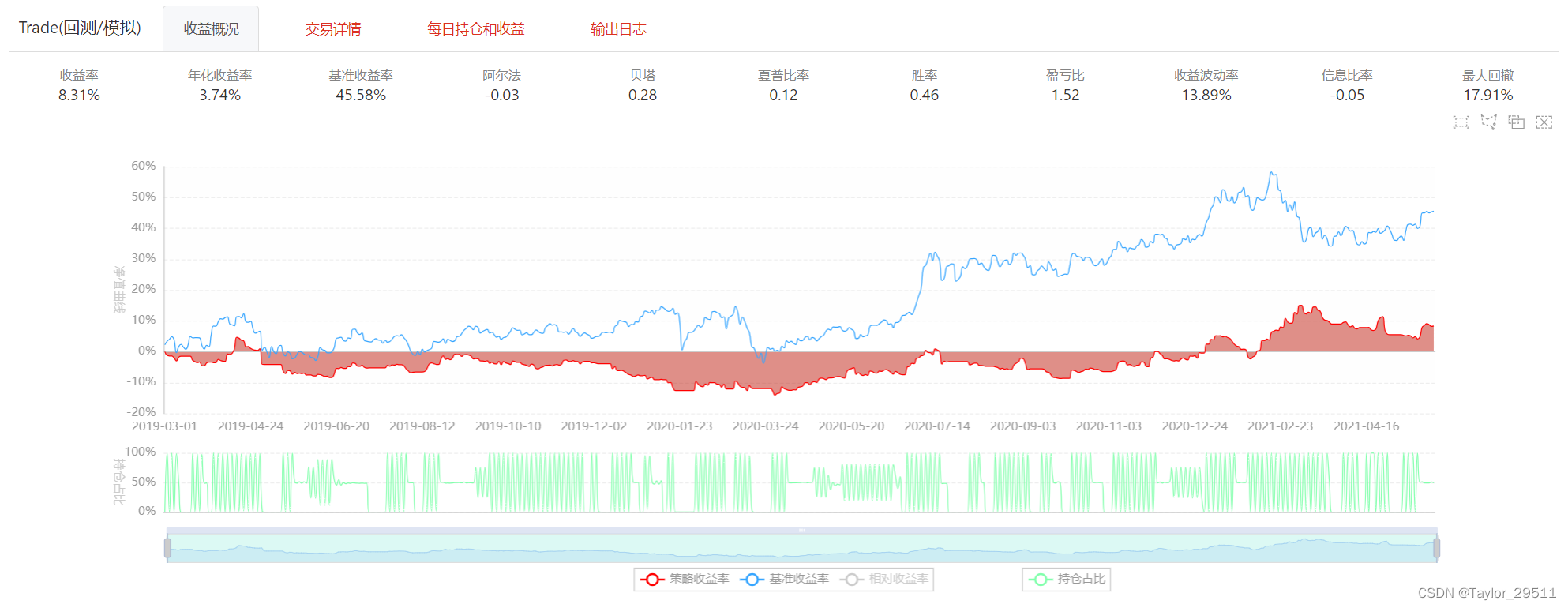
【量化课程】07_量化回测
文章目录 7.1 pandas计算策略评估指标数据准备净值曲线年化收益率波动率最大回撤Alpha系数和Beta系数夏普比率信息比率 7.2 聚宽平台量化回测实践平台介绍策略实现 7.3 Backtrader平台量化回测实践Backtrader简介Backtrader量化回测框架实践 7.4 BigQuant量化框架实战BigQuant简…...
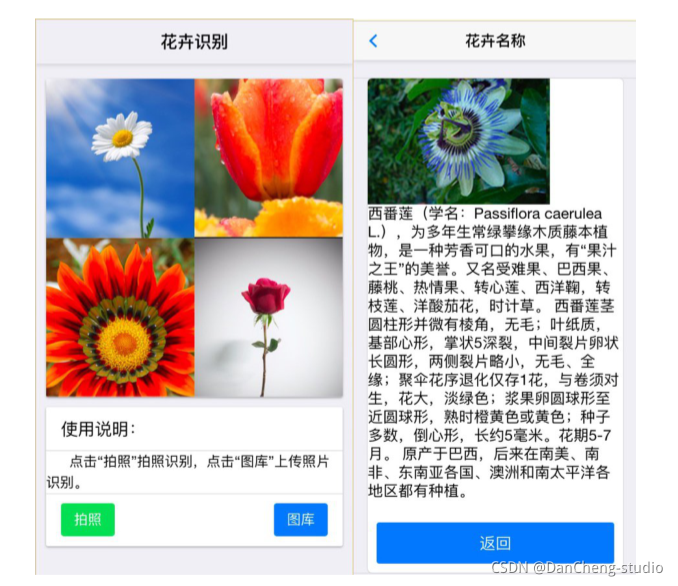
竞赛项目 深度学习花卉识别 - python 机器视觉 opencv
文章目录 0 前言1 项目背景2 花卉识别的基本原理3 算法实现3.1 预处理3.2 特征提取和选择3.3 分类器设计和决策3.4 卷积神经网络基本原理 4 算法实现4.1 花卉图像数据4.2 模块组成 5 项目执行结果6 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 &a…...
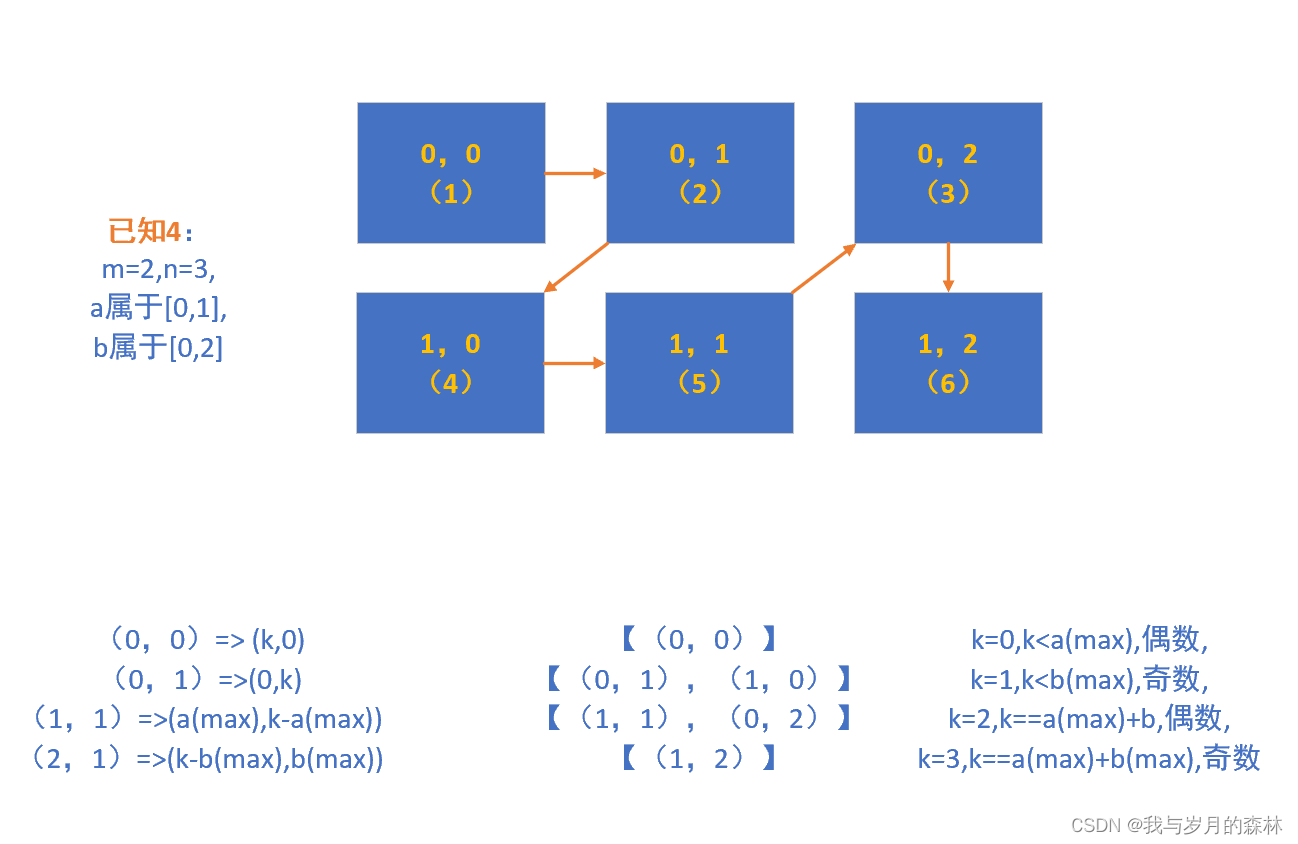
用对角线去遍历矩阵
声明 该系列文章仅仅展示个人的解题思路和分析过程,并非一定是优质题解,重要的是通过分析和解决问题能让我们逐渐熟练和成长,从新手到大佬离不开一个磨练的过程,加油! 原题链接 用对角线遍历矩阵https://leetcode.c…...
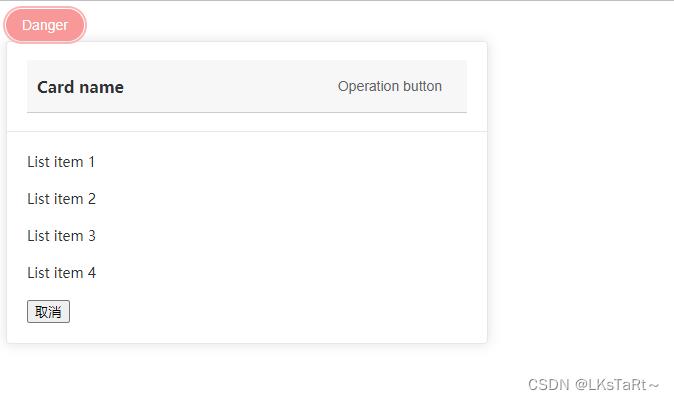
【vue】点击按钮弹出卡片,点击卡片中的取消按钮取消弹出的卡片(附代码)
实现思路: 在按钮上绑定一个点击事件,默认是true;在export default { }中注册变量给卡片标签用v-if判断是否要显示卡片,ture则显示;在卡片里面写好你想要展示的数据;给卡片添加一个取消按钮,绑…...

【K8S】pod 基础概念讲解
目录 Pod基础概念:在Kubrenetes集群中Pod有如下两种使用方式:pause容器使得Pod中的所有容器可以共享两种资源:网络和存储。总结:kubernetes中的pause容器主要为每个容器提供以下功能:Kubernetes设计这样的Pod概念和特殊…...
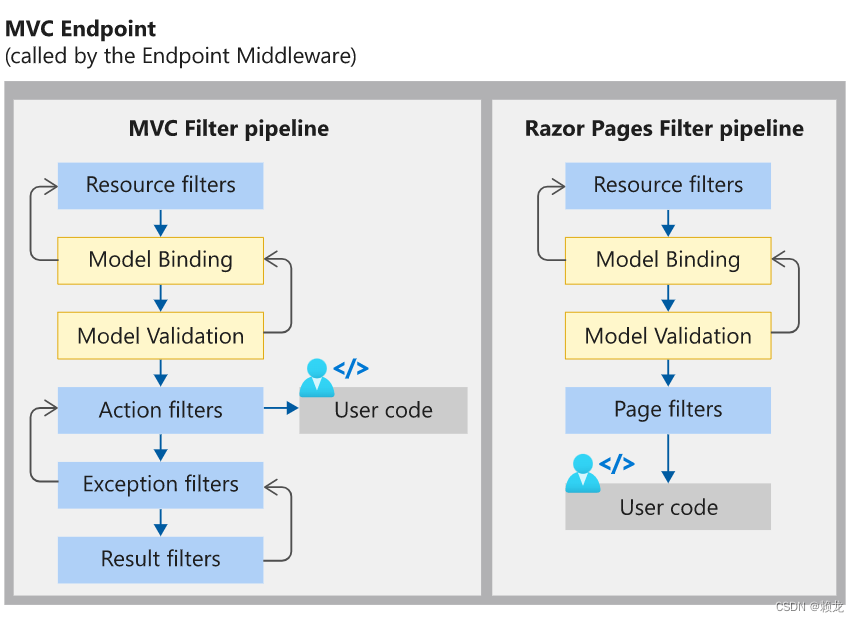
ASP.NET Core中间件记录管道图和内置中间件
管道记录 下图显示了 ASP.NET Core MVC 和 Razor Pages 应用程序的完整请求处理管道 中间件组件在文件中添加的顺序Program.cs定义了请求时调用中间件组件的顺序以及响应的相反顺序。该顺序对于安全性、性能和功能至关重要。 内置中间件记录 内置中间件原文翻译MiddlewareDe…...

[系统安全] 五十二.DataCon竞赛 (1)2020年Coremail钓鱼邮件识别及分类详解
您可能之前看到过我写的类似文章,为什么还要重复撰写呢?只是想更好地帮助初学者了解病毒逆向分析和系统安全,更加成体系且不破坏之前的系列。因此,我重新开设了这个专栏,准备系统整理和深入学习系统安全、逆向分析和恶意代码检测,“系统安全”系列文章会更加聚焦,更加系…...

Android学习之路(3) 布局
线性布局LinearLayout 前几个小节的例程中,XML文件用到了LinearLayout布局,它的学名为线性布局。顾名思义,线性布局 像是用一根线把它的内部视图串起来,故而内部视图之间的排列顺序是固定的,要么从左到右排列…...
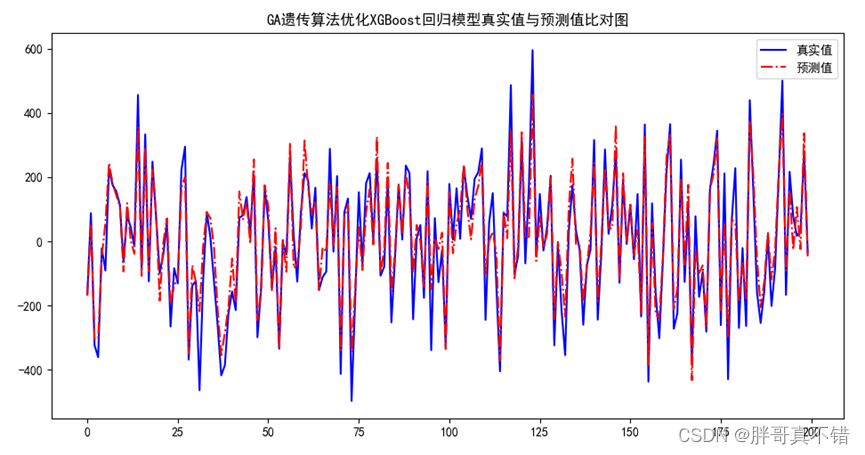
Python实现GA遗传算法优化XGBoost回归模型(XGBRegressor算法)项目实战
说明:这是一个机器学习实战项目(附带数据代码文档视频讲解),如需数据代码文档视频讲解可以直接到文章最后获取。 1.项目背景 遗传算法(Genetic Algorithm,GA)最早是由美国的 John holland于20世…...
C#软件外包开发流程
C# 是一种由微软开发的多范式编程语言,常用于开发各种类型的应用程序,从桌面应用程序到移动应用程序和Web应用程序。下面和大家分享 C# 编程学习流程,希望对大家有所帮助。北京木奇移动技术有限公司,专业的软件外包开发公司&#…...

队列的实现
1.队列的概念 队列:只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列具有先进先出FIFO(First In First Out)。 入队列:进行插入操作的一端称为队尾 出队列:进行删除操作的一端称为队头 2.队列…...

Node + Express 后台开发 —— 起步
Node Express 后台开发 —— 起步 前面陆续学习了一下 node、npm、模块,也稍尝试 Express,感觉得换一个思路加快进行。 比如笔者对前端的开发已较熟悉,如果领导给一个内部小网站的需求,难道说你得给我配置一个后端?…...
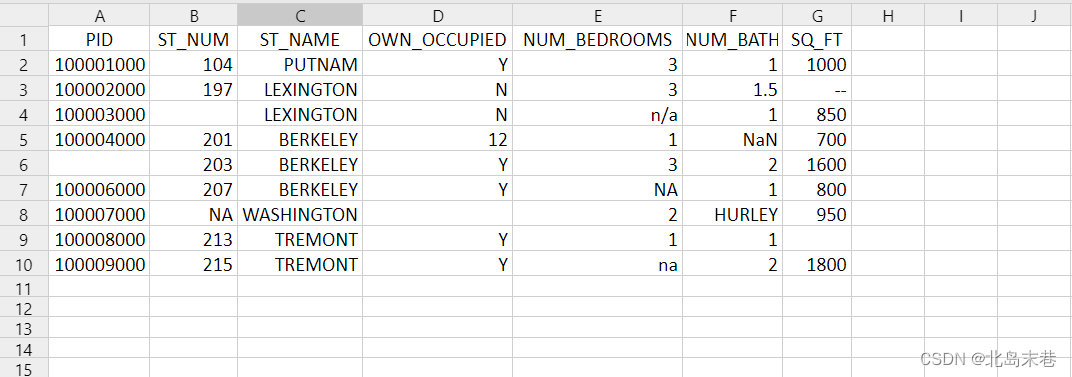
Python学习笔记第五十七天(Pandas 数据清洗)
Python学习笔记第五十七天 Pandas 数据清洗Pandas 清洗空值isnull() Pandas替换单元格mean()median()mode() Pandas 清洗格式错误数据Pandas 清洗错误数据Pandas 清洗重复数据duplicated()drop_duplicates() 后记 Pandas 数据清洗 数据清洗是对一些没有用的数据进行处理的过程…...
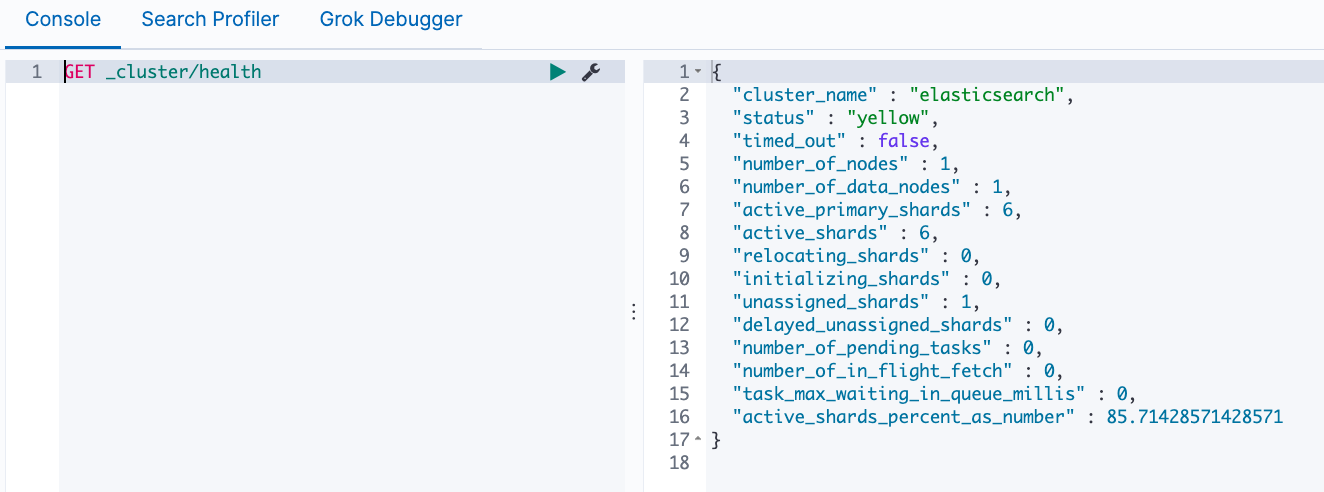
Elasticsearch的一些基本概念
文章目录 基本概念:文档和索引JSON文档元数据索引REST API 节点和集群节点Master eligible节点和Master节点Data Node 和 Coordinating Node其它节点 分片(Primary Shard & Replica Shard)分片的设定操作命令 基本概念:文档和索引 Elasticsearch是面…...

Guitar Pro8专业版吉他学习、绘谱、创作软件
Guitar Pro 8 专业版更强大!更优雅!更完美!Guitar Pro 8.0 五年磨一剑!多达30项功能优化!Guitar Pro8 版本一共更新近30项功能,令吉他打谱更出色!Guitar Pro8 是自2017年4月发布7.0之后发布的最…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...
