0基础学C#笔记10:归并排序法
文章目录
- 前言
- 一、递归的方式
- 二、代码
- 总结
前言
将一个大的无序数组有序,我们可以把大的数组分成两个,然后对这两个数组分别进行排序,之后在把这两个数组合并成一个有序的数组。由于两个小的数组都是有序的,所以在合并的时候是很快的。
一、递归的方式
通过递归的方式将大的数组一直分割,直到数组的大小为 1,此时只有一个元素,那么该数组就是有序的了,之后再把两个数组大小为1的合并成一个大小为2的,再把两个大小为2的合并成4的 …… 直到全部小的数组合并起来。
为方便理解我还准备了动图:

二、代码
public class MergeSort {// 归并排序public static int[] mergeSort(int[] arr, int left, int right) {// 如果 left == right,表示数组只有一个元素,则不用递归排序if (left < right) {// 把大的数组分隔成两个数组int mid = (left + right) / 2;// 对左半部分进行排序arr = mergeSort(arr, left, mid);// 对右半部分进行排序arr = mergeSort(arr, mid + 1, right);//进行合并merge(arr, left, mid, right);}return arr;}// 合并函数,把两个有序的数组合并起来// arr[left..mif]表示一个数组,arr[mid+1 .. right]表示一个数组private static void merge(int[] arr, int left, int mid, int right) {//先用一个临时数组把他们合并汇总起来int[] a = new int[right - left + 1];int i = left;int j = mid + 1;int k = 0;while (i <= mid && j <= right) {if (arr[i] < arr[j]) {a[k++] = arr[i++];} else {a[k++] = arr[j++];}}while(i <= mid) a[k++] = arr[i++];while(j <= right) a[k++] = arr[j++];// 把临时数组复制到原数组for (i = 0; i < k; i++) {arr[left++] = a[i];}}
}
然而面试官要你写个非递归式的归并排序怎么办?别怕,我这还撸了个非递归式的归并排序,代码如下:
public class MergeSort {// 非递归式的归并排序public static int[] mergeSort(int[] arr) {int n = arr.length;// 子数组的大小分别为1,2,4,8...// 刚开始合并的数组大小是1,接着是2,接着4....for (int i = 1; i < n; i += i) {//进行数组进行划分int left = 0;int mid = left + i - 1;int right = mid + i;//进行合并,对数组大小为 i 的数组进行两两合并while (right < n) {// 合并函数和递归式的合并函数一样merge(arr, left, mid, right);left = right + 1;mid = left + i - 1;right = mid + i;}// 还有一些被遗漏的数组没合并,千万别忘了// 因为不可能每个字数组的大小都刚好为 iif (left < n && mid < n) {merge(arr, left, mid, n - 1);}}return arr;}
}
总结
性质:
1、时间复杂度:O(nlogn)
2、空间复杂度:O(n)
3、稳定排序
4、非原地排序
相关文章:

0基础学C#笔记10:归并排序法
文章目录 前言一、递归的方式二、代码总结 前言 将一个大的无序数组有序,我们可以把大的数组分成两个,然后对这两个数组分别进行排序,之后在把这两个数组合并成一个有序的数组。由于两个小的数组都是有序的,所以在合并的时候是很…...

nlohmann json:通过for遍历object和array
object和array可以使用数for进行遍历: #include <iostream> #include <nlohmann/json.hpp> using namespace std; using json = nlohmann::json;auto checkJsonType(json& x) {if(x.type() == json::value_t::null){cout<<x<<" is null&quo…...

适配器模式:将不兼容的接口转换为可兼容的接口
适配器模式:将不兼容的接口转换为可兼容的接口 什么是适配器模式? 适配器模式是一种结构型设计模式,用于将一个类的接口转换为客户端所期望的另一个接口。它允许不兼容的类能够合作,使得原本由于接口不匹配而无法工作的类能够一…...
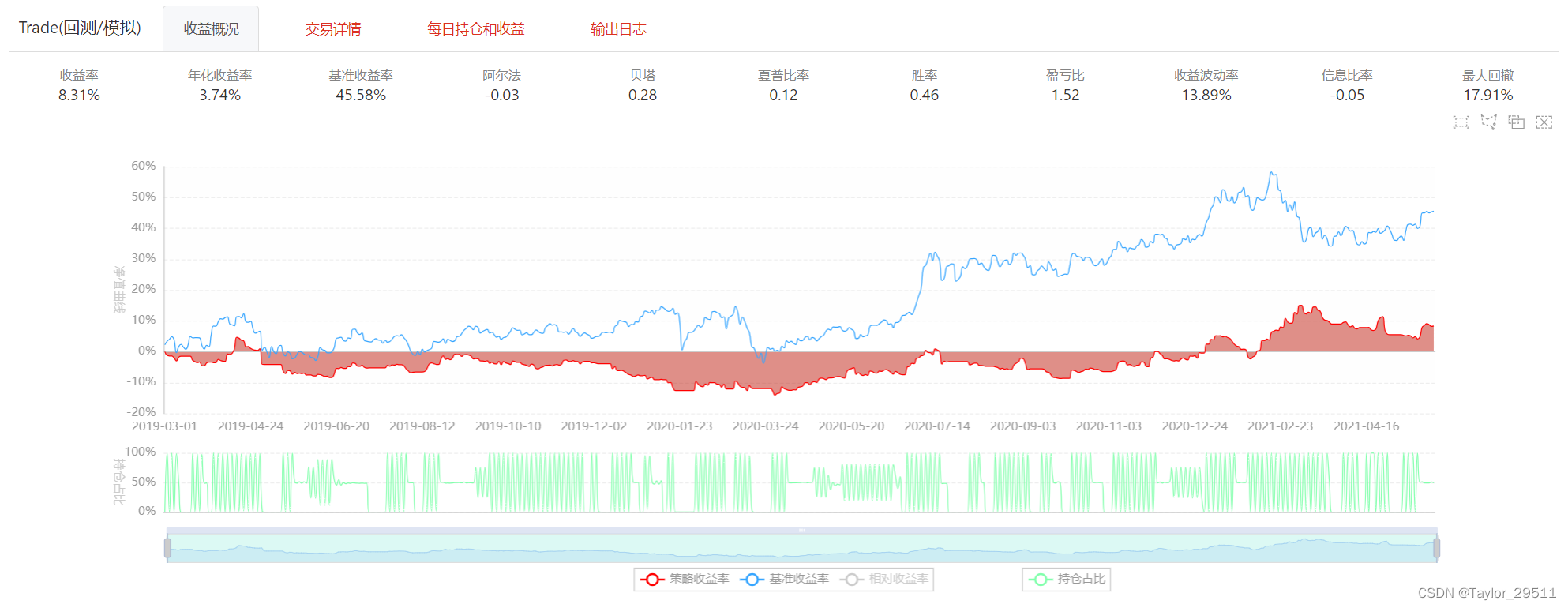
【量化课程】07_量化回测
文章目录 7.1 pandas计算策略评估指标数据准备净值曲线年化收益率波动率最大回撤Alpha系数和Beta系数夏普比率信息比率 7.2 聚宽平台量化回测实践平台介绍策略实现 7.3 Backtrader平台量化回测实践Backtrader简介Backtrader量化回测框架实践 7.4 BigQuant量化框架实战BigQuant简…...
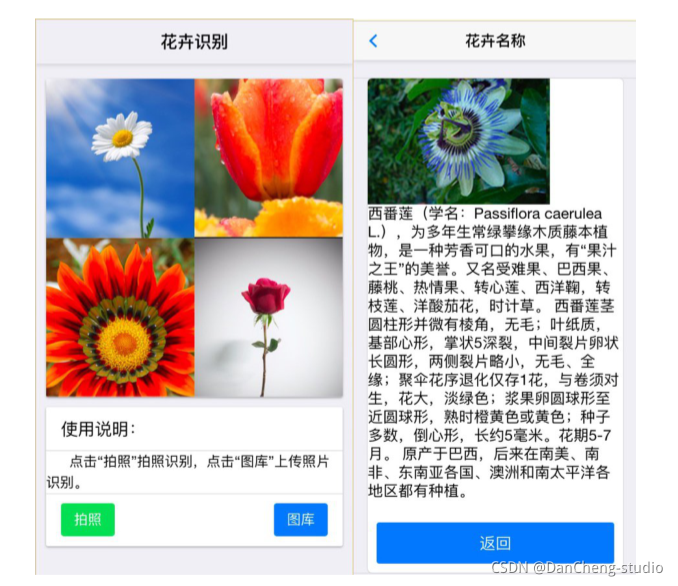
竞赛项目 深度学习花卉识别 - python 机器视觉 opencv
文章目录 0 前言1 项目背景2 花卉识别的基本原理3 算法实现3.1 预处理3.2 特征提取和选择3.3 分类器设计和决策3.4 卷积神经网络基本原理 4 算法实现4.1 花卉图像数据4.2 模块组成 5 项目执行结果6 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 &a…...
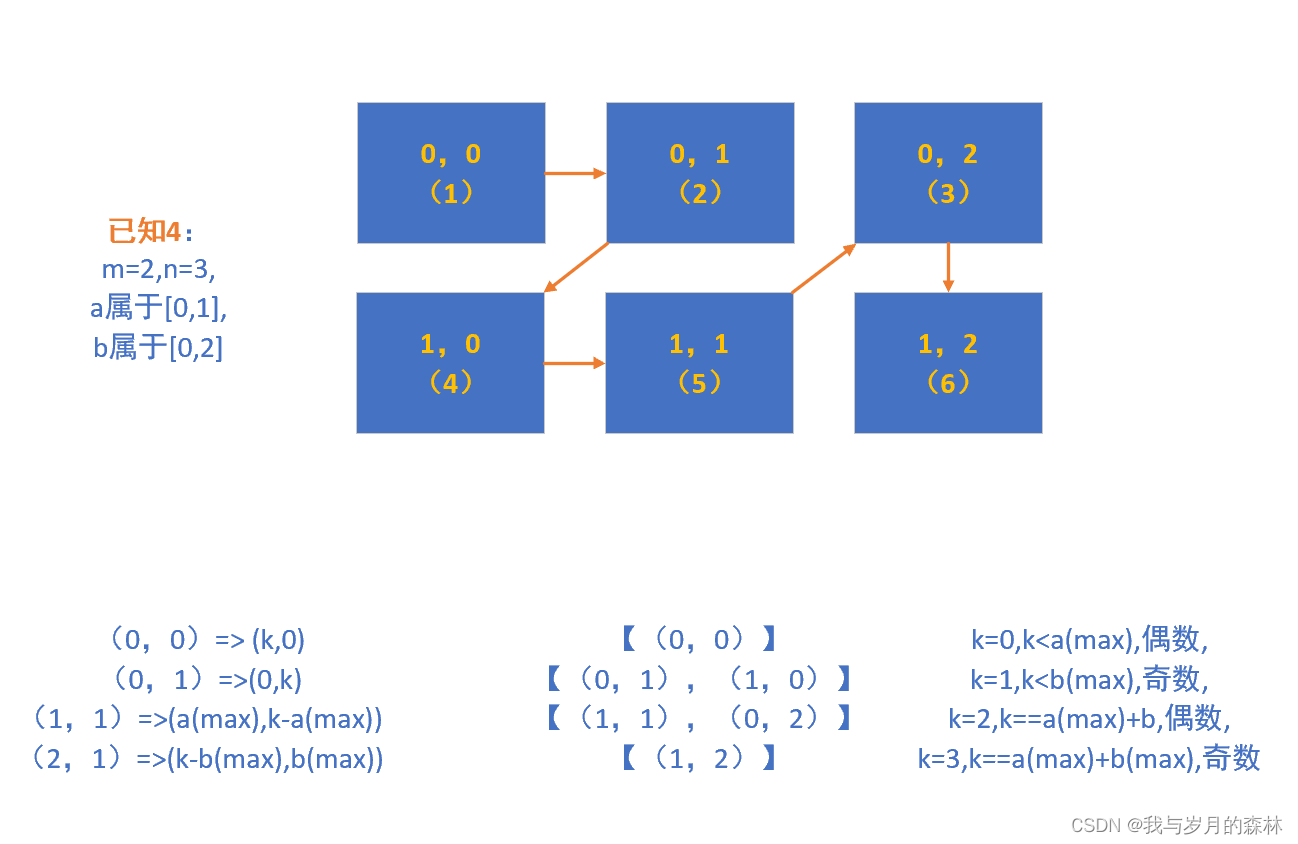
用对角线去遍历矩阵
声明 该系列文章仅仅展示个人的解题思路和分析过程,并非一定是优质题解,重要的是通过分析和解决问题能让我们逐渐熟练和成长,从新手到大佬离不开一个磨练的过程,加油! 原题链接 用对角线遍历矩阵https://leetcode.c…...
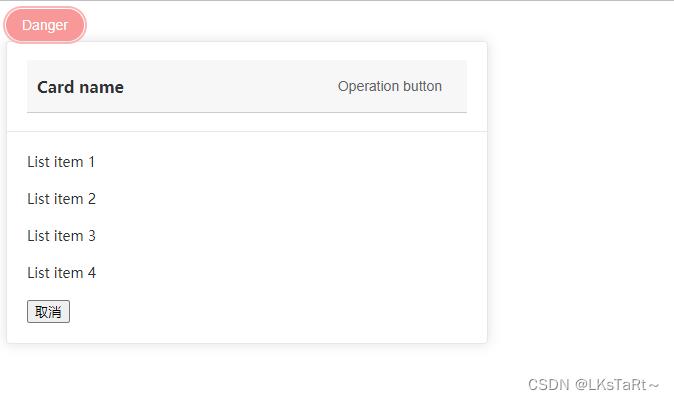
【vue】点击按钮弹出卡片,点击卡片中的取消按钮取消弹出的卡片(附代码)
实现思路: 在按钮上绑定一个点击事件,默认是true;在export default { }中注册变量给卡片标签用v-if判断是否要显示卡片,ture则显示;在卡片里面写好你想要展示的数据;给卡片添加一个取消按钮,绑…...

【K8S】pod 基础概念讲解
目录 Pod基础概念:在Kubrenetes集群中Pod有如下两种使用方式:pause容器使得Pod中的所有容器可以共享两种资源:网络和存储。总结:kubernetes中的pause容器主要为每个容器提供以下功能:Kubernetes设计这样的Pod概念和特殊…...
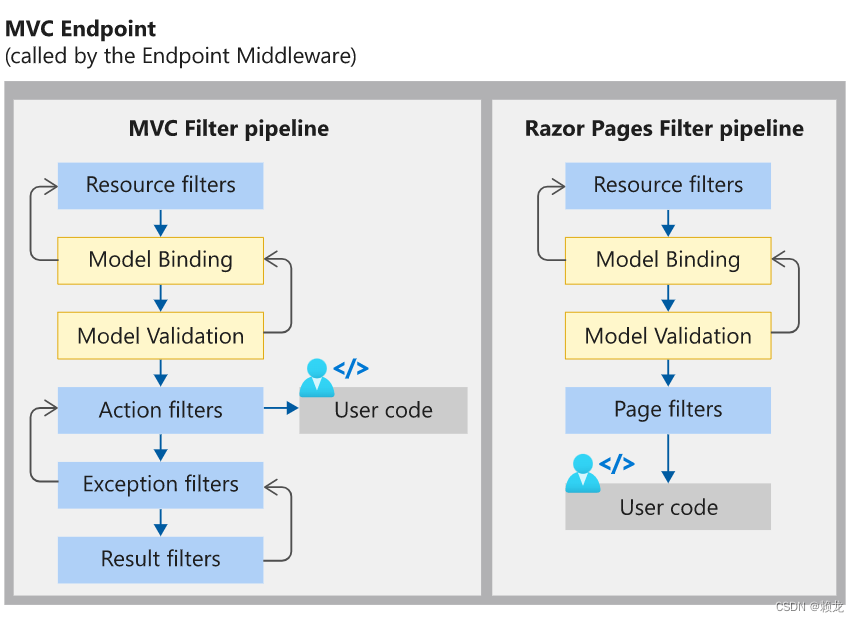
ASP.NET Core中间件记录管道图和内置中间件
管道记录 下图显示了 ASP.NET Core MVC 和 Razor Pages 应用程序的完整请求处理管道 中间件组件在文件中添加的顺序Program.cs定义了请求时调用中间件组件的顺序以及响应的相反顺序。该顺序对于安全性、性能和功能至关重要。 内置中间件记录 内置中间件原文翻译MiddlewareDe…...

[系统安全] 五十二.DataCon竞赛 (1)2020年Coremail钓鱼邮件识别及分类详解
您可能之前看到过我写的类似文章,为什么还要重复撰写呢?只是想更好地帮助初学者了解病毒逆向分析和系统安全,更加成体系且不破坏之前的系列。因此,我重新开设了这个专栏,准备系统整理和深入学习系统安全、逆向分析和恶意代码检测,“系统安全”系列文章会更加聚焦,更加系…...

Android学习之路(3) 布局
线性布局LinearLayout 前几个小节的例程中,XML文件用到了LinearLayout布局,它的学名为线性布局。顾名思义,线性布局 像是用一根线把它的内部视图串起来,故而内部视图之间的排列顺序是固定的,要么从左到右排列…...
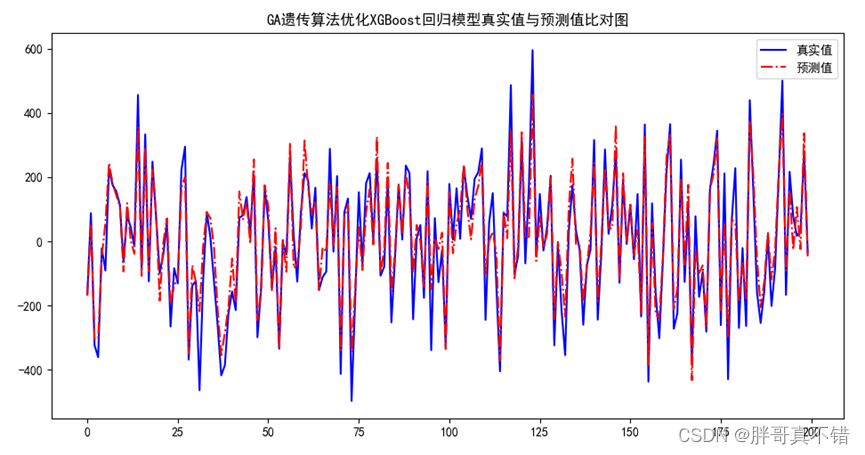
Python实现GA遗传算法优化XGBoost回归模型(XGBRegressor算法)项目实战
说明:这是一个机器学习实战项目(附带数据代码文档视频讲解),如需数据代码文档视频讲解可以直接到文章最后获取。 1.项目背景 遗传算法(Genetic Algorithm,GA)最早是由美国的 John holland于20世…...
C#软件外包开发流程
C# 是一种由微软开发的多范式编程语言,常用于开发各种类型的应用程序,从桌面应用程序到移动应用程序和Web应用程序。下面和大家分享 C# 编程学习流程,希望对大家有所帮助。北京木奇移动技术有限公司,专业的软件外包开发公司&#…...

队列的实现
1.队列的概念 队列:只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列具有先进先出FIFO(First In First Out)。 入队列:进行插入操作的一端称为队尾 出队列:进行删除操作的一端称为队头 2.队列…...

Node + Express 后台开发 —— 起步
Node Express 后台开发 —— 起步 前面陆续学习了一下 node、npm、模块,也稍尝试 Express,感觉得换一个思路加快进行。 比如笔者对前端的开发已较熟悉,如果领导给一个内部小网站的需求,难道说你得给我配置一个后端?…...
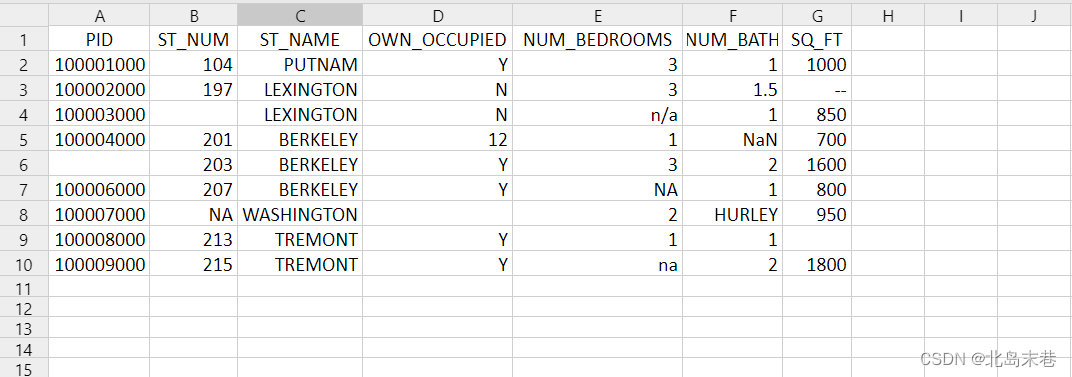
Python学习笔记第五十七天(Pandas 数据清洗)
Python学习笔记第五十七天 Pandas 数据清洗Pandas 清洗空值isnull() Pandas替换单元格mean()median()mode() Pandas 清洗格式错误数据Pandas 清洗错误数据Pandas 清洗重复数据duplicated()drop_duplicates() 后记 Pandas 数据清洗 数据清洗是对一些没有用的数据进行处理的过程…...
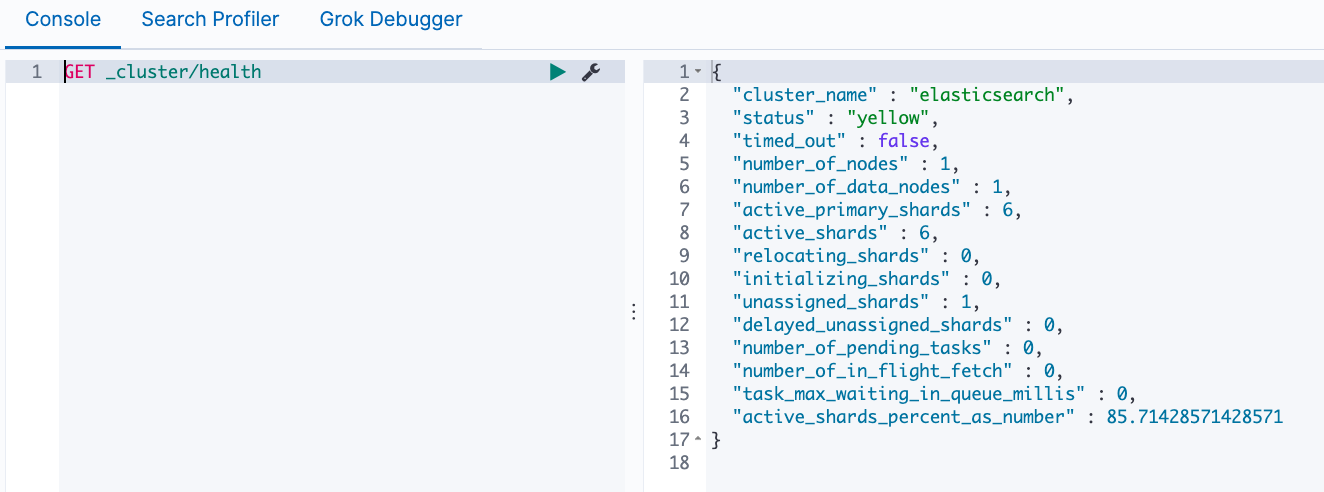
Elasticsearch的一些基本概念
文章目录 基本概念:文档和索引JSON文档元数据索引REST API 节点和集群节点Master eligible节点和Master节点Data Node 和 Coordinating Node其它节点 分片(Primary Shard & Replica Shard)分片的设定操作命令 基本概念:文档和索引 Elasticsearch是面…...

Guitar Pro8专业版吉他学习、绘谱、创作软件
Guitar Pro 8 专业版更强大!更优雅!更完美!Guitar Pro 8.0 五年磨一剑!多达30项功能优化!Guitar Pro8 版本一共更新近30项功能,令吉他打谱更出色!Guitar Pro8 是自2017年4月发布7.0之后发布的最…...
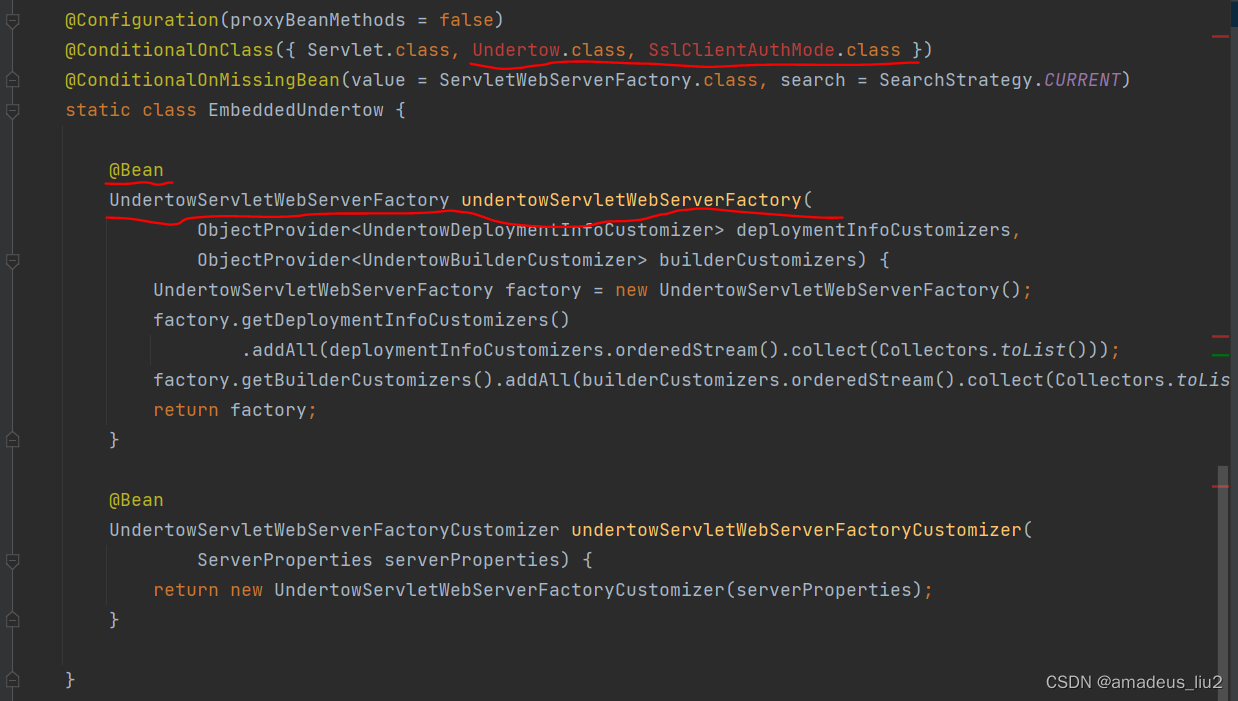
SpringBoot复习(39)Servlet容器的自动配置原理
Servlet容器自动配置类为ServletWebServerFactoryAutoConfiguration 可以看到通过Import注解导入了三个配置类: 通过这个这三个配置类可以看出,它们都使用了ConditionalOnClass注解,当类路径存在tomcat相关的类时,会配置一个T…...

【前端 | CSS】盒模型clientWidth、clientHeight、offsetWidht、offsetHeight
图 先看一个例子 html <div class"container"><div class"item">内容内容内容内容内容内容内容内容内容内容内容内容内容内容内容内容内容内容内容内容内容内容内容内容内容内容内容内容内容内容内容内容内容内容内容内容</div> </…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...
