nlohmann json:检查object是否存在某个键
1.通过find进行检查
#include <iostream>
#include <nlohmann/json.hpp>
using namespace std;
using json = nlohmann::json;int main()
{json data = R"({"name": "xiaoming","age": 10, "parent": [{"father" : "zhang","age" : 40},{"mother" : "wang","age" : 36}]})"_json;auto ifFind = data.find("name");if(ifFind != data.end()){cout<<"name="<<data["name"]<<endl;}else{cout<<"name not exist"<<endl;}ifFind = data.find("address");if(ifFind != data.end()){cout<<相关文章:

nlohmann json:检查object是否存在某个键
1.通过find进行检查 #include <iostream> #include <nlohmann/json.hpp> using namespace std; using json = nlohmann::json;int main() {json data = R"({"name": "xiaoming","age": 10, "parent": [{"fat…...
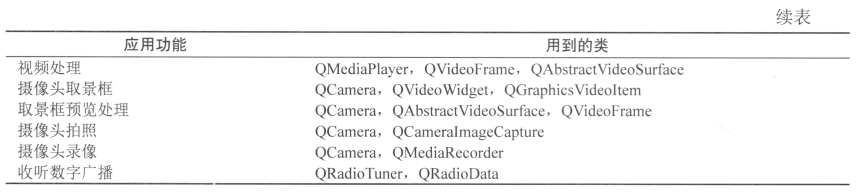
15-1_Qt 5.9 C++开发指南_Qt多媒体模块概述
多媒体功能指的主要是计算机的音频和视频的输入、输出、显示和播放等功能,Qt 的多媒体模块为音频和视频播放、录音、摄像头拍照和录像等提供支持,甚至还提供数字收音机的支持。本章将介绍 Qt 多媒体模块的功能和使用。 文章目录 1. Qt 多媒体模块概述2. …...

分页查询中起始位置的计算
在分页查询中,page 和 pageSize 其实就是表示页数和每页的条数。这两个参数通常用于在数据库查询时进行分页。 如果你想根据 page 和 pageSize 计算数据的起始位置(例如,MySQL数据库的LIMIT查询),可以使用以下公式&am…...

Failed to execute goal org.apache.maven.plugins
原因: 这个文件D:\java\maven\com\ruoyi\pg-student\maven-metadata-local.xml出了问题 解决: 最简单的直接删除D:\java\maven\com\ruoyi\pg-student\maven-metadata-local.xml重新打包 或者把D:\java\maven\com\ruoyi\pg-student这个目录下所有文件…...

50吨收费站生活一体化污水处理设备厂家价格低
50吨收费站生活一体化污水处理设备厂家价格低 设备工艺说明 污水处理设备主要用于生活污水和与之类似的工业有机废水的处理,其主要处理方法是采用目前较为成熟的生化处理技术—生物接触氧化,水质设计按一般生活污水水质设计计算,按BOD5平均20…...
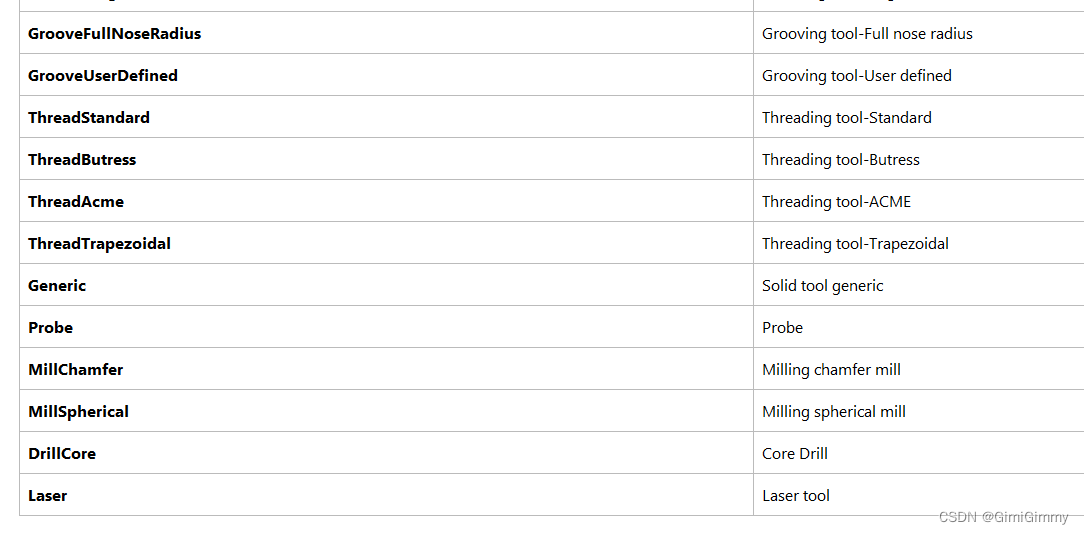
UG NX二次开发(C#)-CAM-获取刀具类型
文章目录 1、前言2、UG NX中的刀具类型3、获取刀具类型3.1 刀具类型帮助文档1、前言 在UG NX的加工模块,加工刀具是一个必要的因素,其包括了多种类型的类型,有铣刀、钻刀、车刀、磨刀、成型刀等等,而且每种刀具所包含的信息也各不相同。想获取刀具的信息,那就要知道刀具的…...
Flask 框架集成Bootstrap
前面学习了 Flask 框架的基本用法,以及模板引擎 Jinja2,按理说可以开始自己的 Web 之旅了,不过在启程之前,还有个重要的武器需要了解一下,就是著名的 Bootstrap 框架和 Flask 的结合,这将大大提高开发 Web …...

在k8s 1.26.6上部署ES集群
一、k8s集群架构: IP 角色,左边是ip,右边是hostname master1 是192.168.1.3 的hostname 192.168.1.3 master1 192.168.1.4 master2 192.168.1.5 master3 192.168.1.6 node1 192.168.1.7 node2 二、部署ES集群 1、配置stor…...

用神经网络玩转数据聚类:自编码器的原理与实践
目录 引言一、什么是自编码器二、自编码器的应用场景三、自编码器的优缺点四、如何实现基于自编码器的聚类算法五、总结 引言 随着数据量的爆炸性增长,如何有效地处理和分析数据成为了一个重要的问题。数据聚类是一种常用的数据分析方法,它可以将数据集…...

Linux系统调试课:Linux Kernel Printk
🚀返回专栏总目录 文章目录 0、printk 说明1、printk 日志等级设置2、屏蔽等级日志控制机制3、printk打印常用方式4、printk打印格式0、printk 说明 在开发Linux device Driver或者跟踪调试内核行为的时候经常要通过Log API来trace整个过程,Kernel API printk()是整个Kern…...
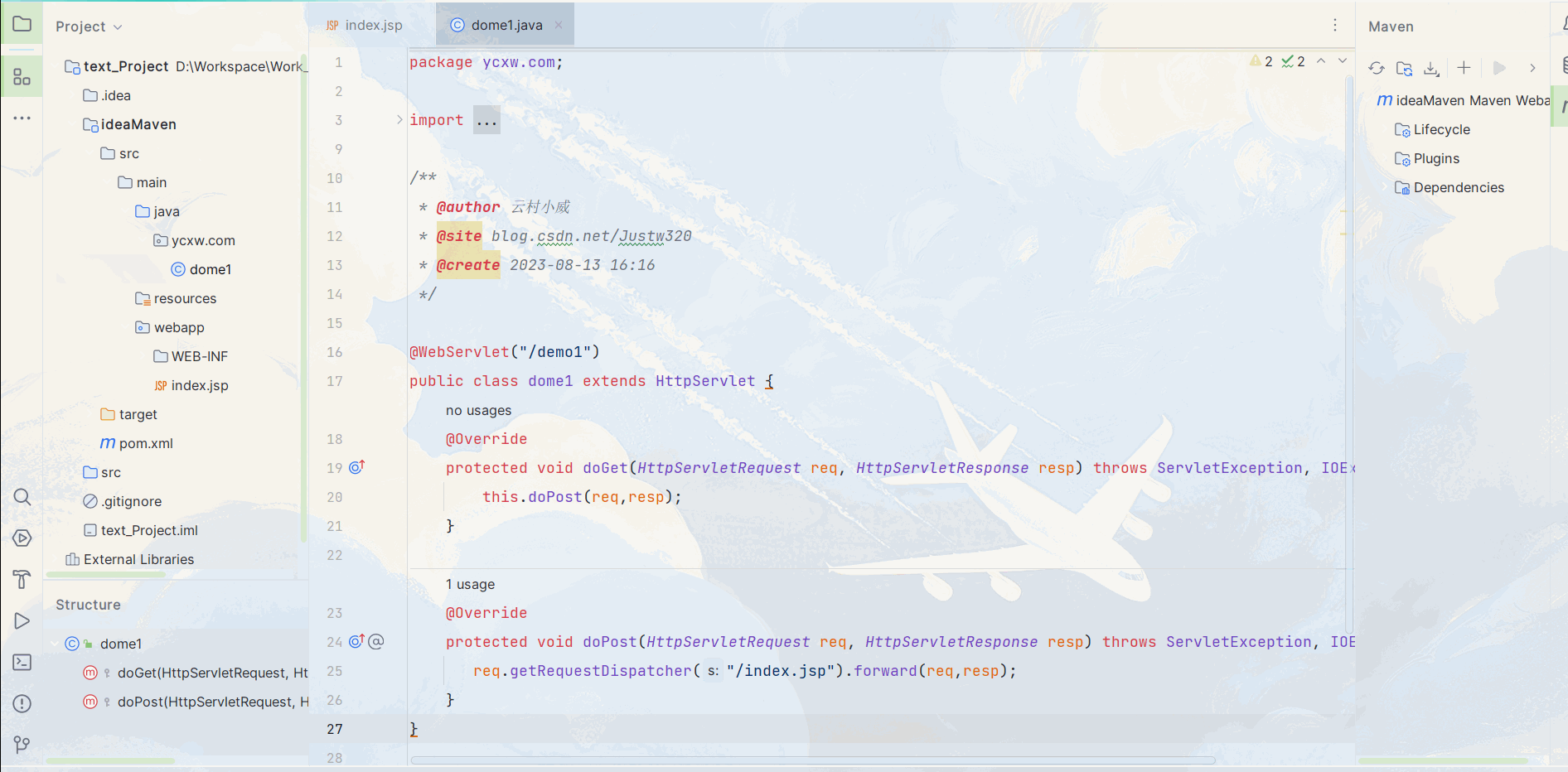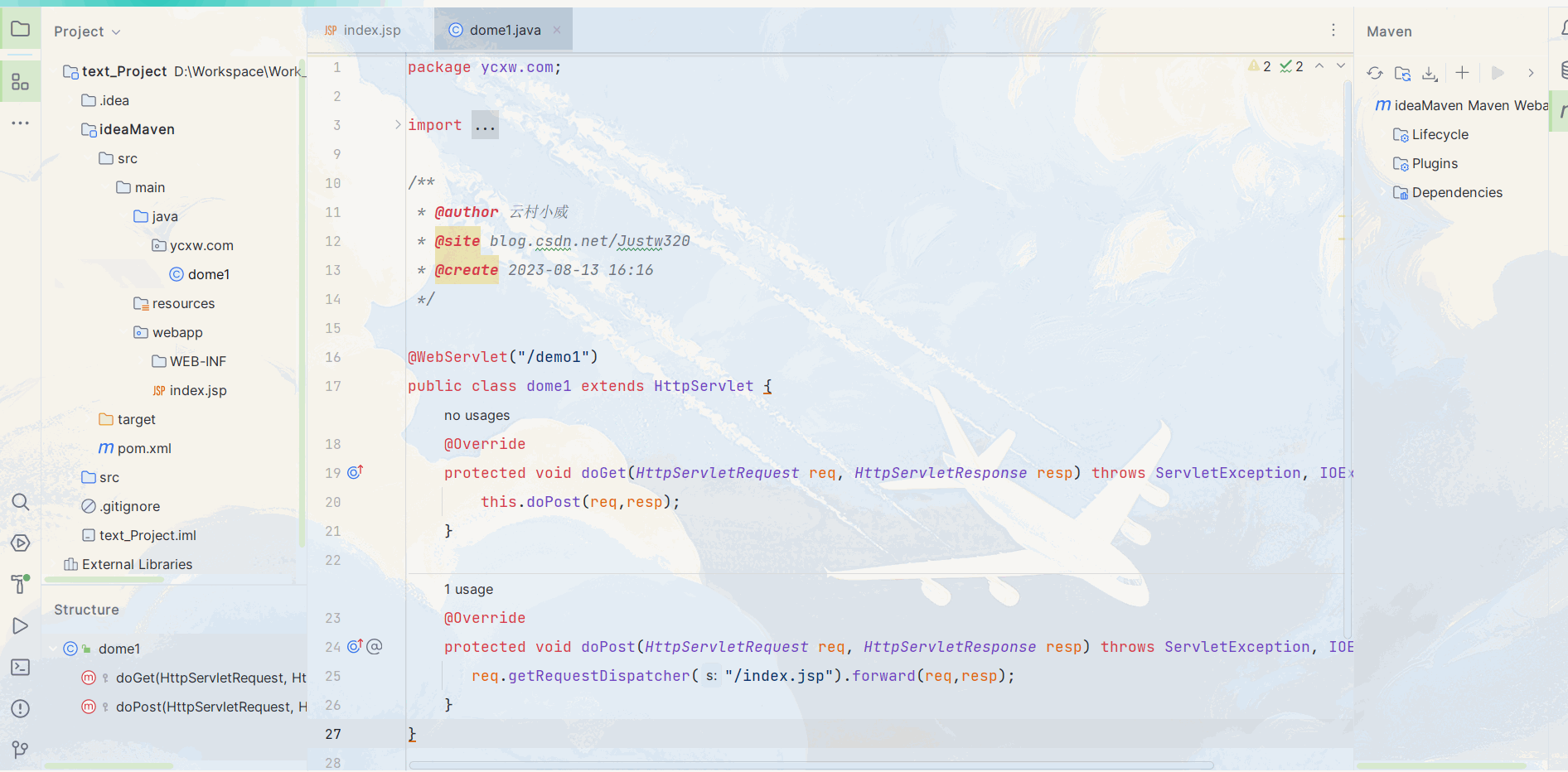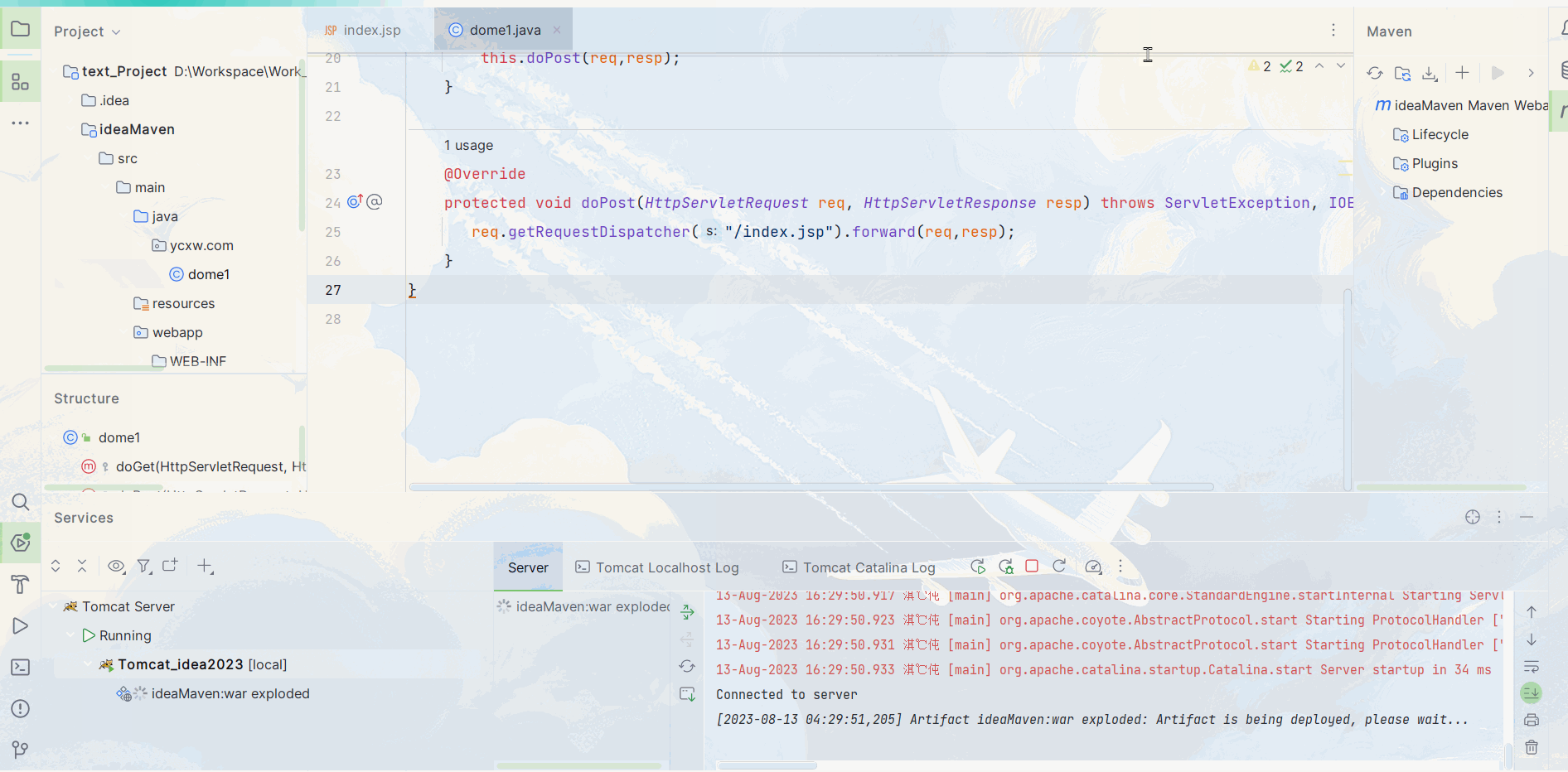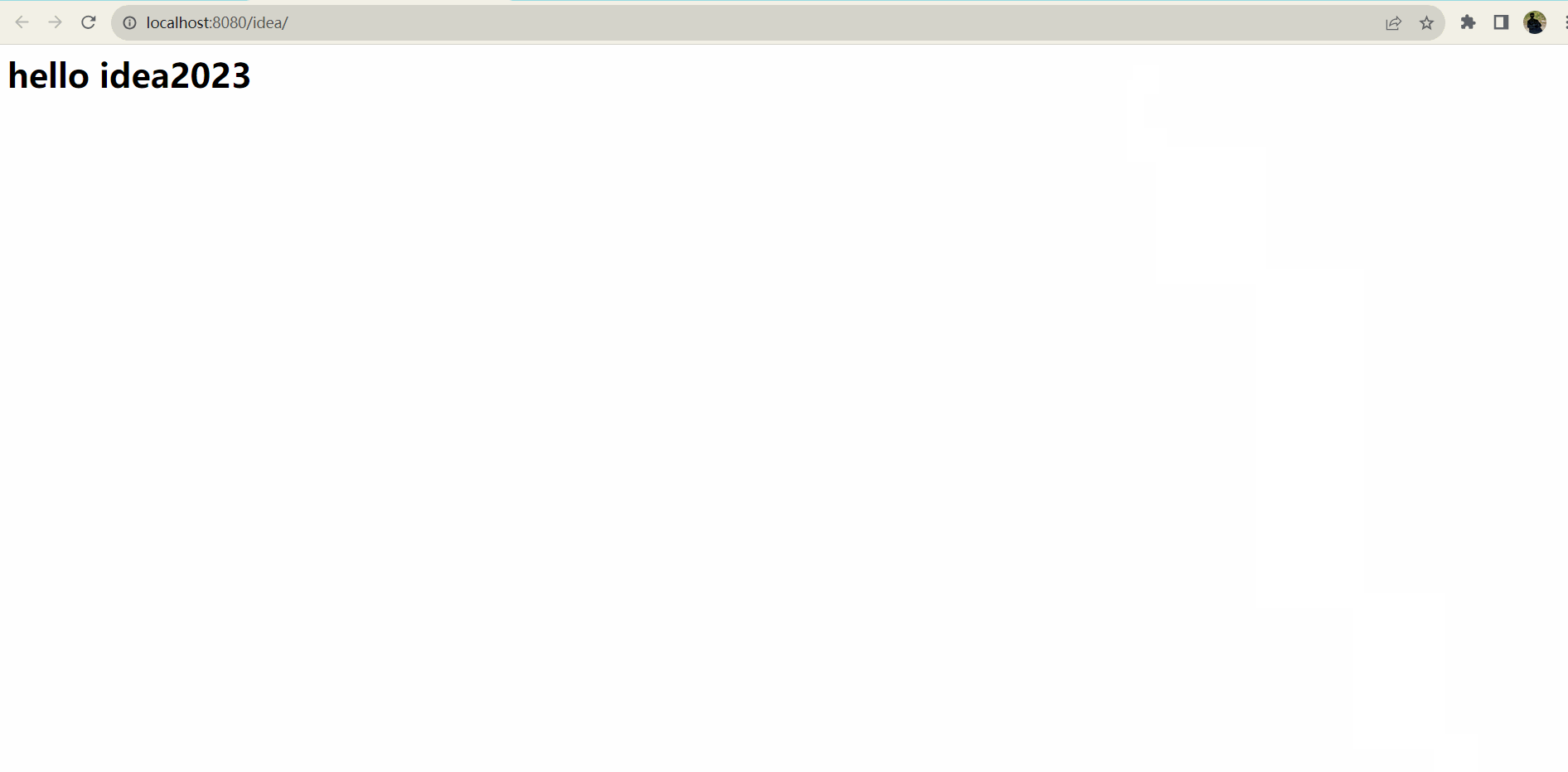
不同版本Idea部署Maven和Tomcat教学
目录 一、2019版Idea 1.1. Maven配置 1.2. Tomcat配置 二、2023版Idea 2.1 Maven配置 2.2. Tomcat配置 一、2019版Idea 1.1. Maven配置 在这篇 http://t.csdn.cn/oetKq 我已经详细讲述了Maven的下载安装及配置,本篇就直接开始实操 : 1. 首先进入设置搜索Mave…...

Vue 3.0中的Treeshaking?
1.treeshaking是什么? Tree shaking 是一种通过清除多余代码方式来优化项目打包体积的技术,专业术语叫 Dead code elimination 简单来讲,就是在保持代码运行结果不变的前提下,去除无用的代码 如果把代码打包比作制作蛋糕&#…...
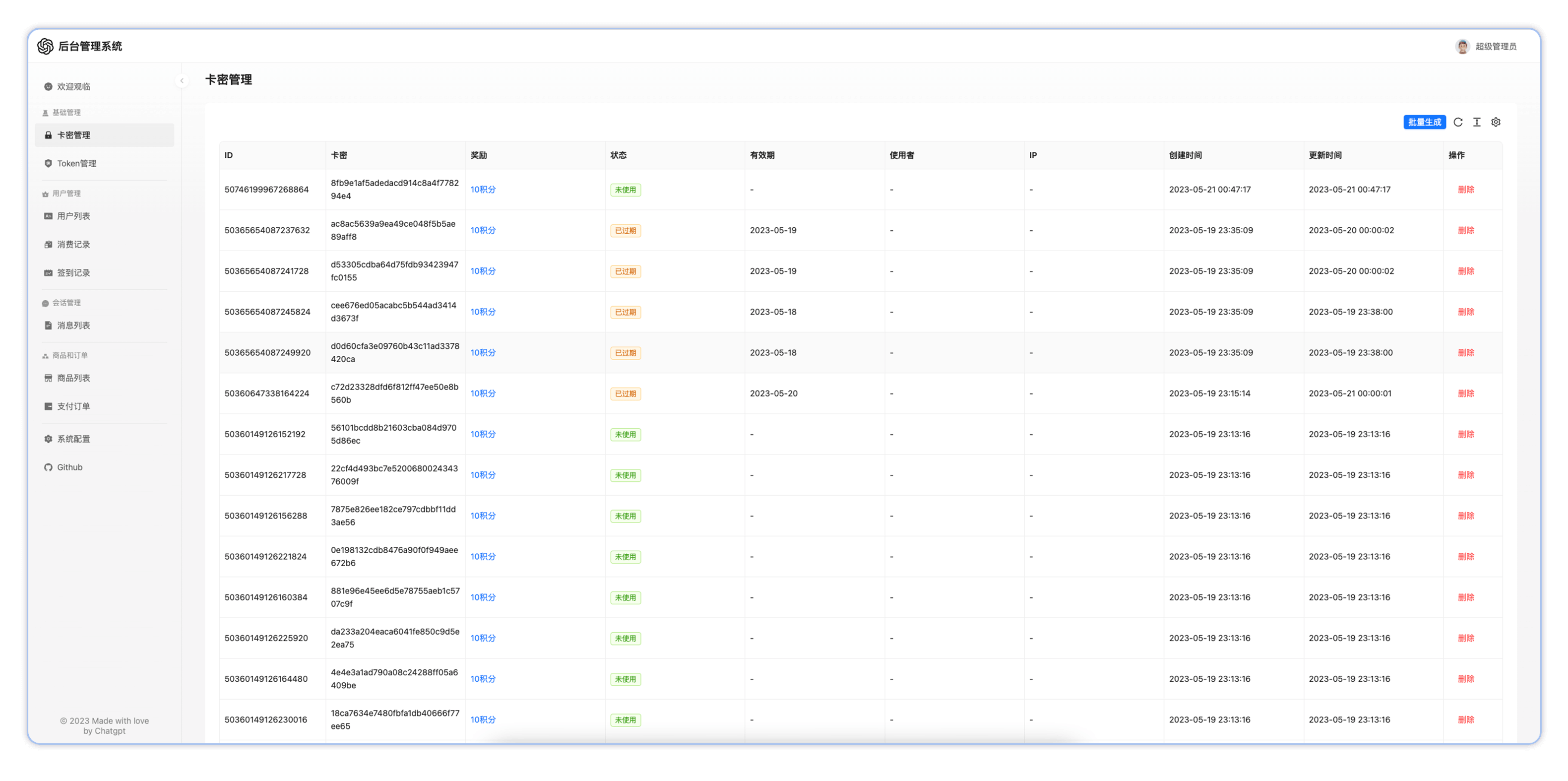
开源可商业运营的ChatGpt网页源码v1.2.2
🤖 主要功能 后台管理系统,可对用户,Token,商品,卡密等进行管理 精心设计的 UI,响应式设计 极快的首屏加载速度(~100kb) 支持Midjourney绘画和DALLE模型绘画,GPT4等应用 海量的内置 prompt 列表,来自中文和英文 一键导…...

驱动阿托斯DLHZO-T伺服比例阀放大器定制
DLHZO-T型伺服比例换向阀,直动式,带LVDT位置传感器和阀芯零遮盖,可应用于各种位置闭环控制实现最佳的性能。 比例阀和模块式数字放大器配合使用。 LVDT传感器和阀套结构可确保非常高的调节精度和响应灵敏度。 失电保护位可实现在电源中断的…...
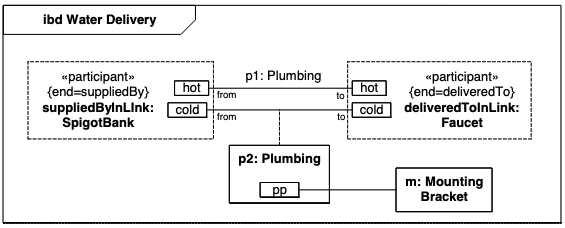
SysML V1.2 Blocks
本人看的实在是太枯燥了,很多都是机翻过了一遍 后面复习的时候,我再用chatgpt润色一下 一、综述 块是系统描述的模块化单元。每个块定义了一组特征来描述系统或其他感兴趣的元素。这些可能包括结构和行为特征,例如属性和操作,以…...

反编译微信小程序,可导出uniapp或taro项目
微信小程序反编译(全网通用) 微信小程序反编译 反编译主要分为四个阶段 操作流程 1. node.js安装 2. node安装模块 3. 开始反编译 4. 导入到微信开发者工具既可运行 微信小程序反编译 当碰到不会写的小程序功能时,正好看到隔壁小程序有类似…...
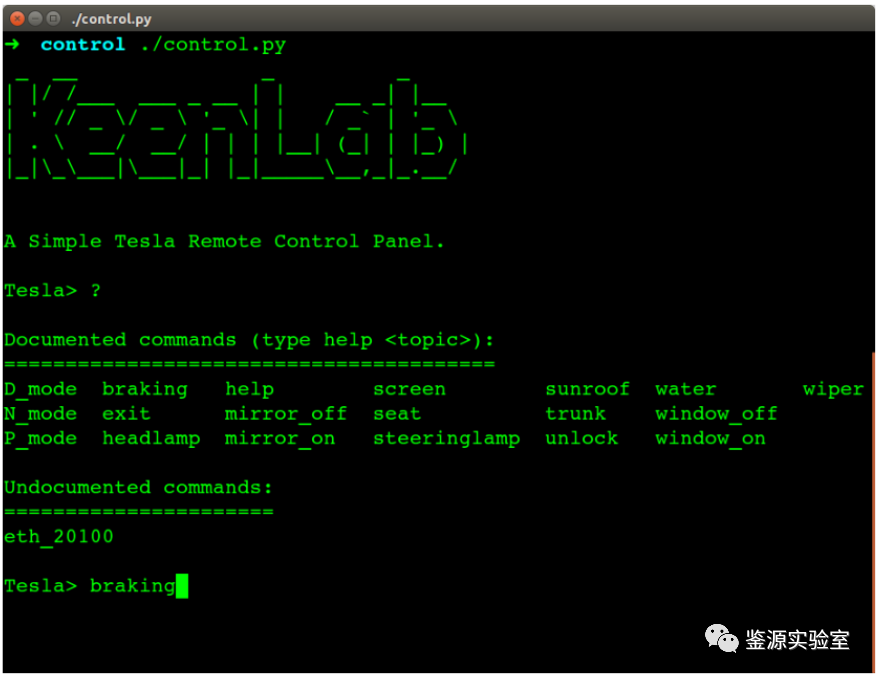
鉴源实验室丨汽车网络安全攻击实例解析(二)
作者 | 田铮 上海控安可信软件创新研究院项目经理 来源 | 鉴源实验室 社群 | 添加微信号“TICPShanghai”加入“上海控安51fusa安全社区” 引言:汽车信息安全事件频发使得汽车行业安全态势愈发紧张。这些汽车网络安全攻击事件,轻则给企业产品发布及产品…...
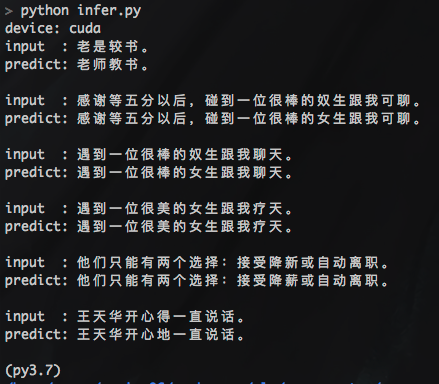
pycorrector一键式文本纠错工具,整合了BERT、MacBERT、ELECTRA、ERNIE等多种模型,让您立即享受纠错的便利和效果
pycorrector:一键式文本纠错工具,整合了Kenlm、ConvSeq2Seq、BERT、MacBERT、ELECTRA、ERNIE、Transformer、T5等多种模型,让您立即享受纠错的便利和效果 pycorrector: 中文文本纠错工具。支持中文音似、形似、语法错误纠正,pytho…...

Linux 日志管理
Linux 日志管理 一.Linux 下的日志服务简介 1.1 CentOS5 之前的版本 centos5 之前的版本使用系统和内核日志分离的格式记录日志 syslogd:该服务专门用于记录系统日志(system application logs) klogd: 该服务专门用于记录内核日志(linux kernel logs) centos5 之前事件的记录格…...

统计学补充概念04-最大似然估计
概念 最大似然估计(Maximum Likelihood Estimation,简称MLE)是一种统计方法,用于估计模型的参数,使得给定观测数据的似然函数达到最大。在最大似然估计中,我们寻找能够最大化观测数据的可能性(…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...
