二叉树题目:二叉树的直径
文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 解法
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:二叉树的直径
出处:543. 二叉树的直径
难度
3 级
题目描述
要求
给定二叉树的根结点 root \texttt{root} root,返回其直径长度。
二叉树的直径是任意两个结点之间的最长路径长度。这条路径可能穿过也可能不穿过根结点。
两个结点之间的路径长度由它们之间边的数目表示。
示例
示例 1:
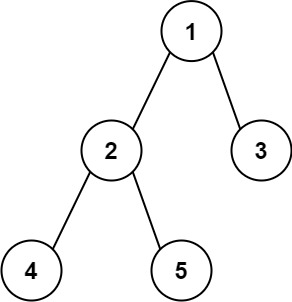
输入: root = [1,2,3,4,5] \texttt{root = [1,2,3,4,5]} root = [1,2,3,4,5]
输出: 3 \texttt{3} 3
解释: 3 \texttt{3} 3 是路径 [4,2,1,3] \texttt{[4,2,1,3]} [4,2,1,3] 或 [5,2,1,3] \texttt{[5,2,1,3]} [5,2,1,3] 的长度。
示例 2:
输入: root = [1,2] \texttt{root = [1,2]} root = [1,2]
输出: 1 \texttt{1} 1
数据范围
- 树中结点数目在范围 [1, 10 4 ] \texttt{[1, 10}^\texttt{4}\texttt{]} [1, 104] 内
- -100 ≤ Node.val ≤ 100 \texttt{-100} \le \texttt{Node.val} \le \texttt{100} -100≤Node.val≤100
解法
思路和算法
二叉树中的任意一条路径一定经过某个子树的根结点,子树可以是二叉树本身。
对于任意一个子树而言,经过该子树根结点的最长路径(以下称为「最长路径」,均指包含根结点的最长路径)一定满足以下条件:如果左子树不为空,则最长路径的左端是左子树的最深叶结点,否则最长路径的左端是根结点;如果右子树不为空,则最长路径的右端是右子树的最深叶结点,否则最长路径的右端是根结点。因此,子树的最长路径长度为该子树的左子树和右子树的深度之和,子树的深度为该子树的左子树和右子树的深度的较大值加 1 1 1。此处的深度定义为二叉树中结点的层数,如果二叉树为空则深度为 0 0 0,如果二叉树只有一个结点则深度为 1 1 1。
由于二叉树的最长路径长度和二叉树的深度都取决于左子树和右子树的深度,因此可以使用深度优先搜索计算二叉树的深度,计算过程中得到二叉树的直径。
计算二叉树的深度的过程是一个递归的过程,递归的终止条件是当前结点为空,此时深度为 0 0 0。其余情况下,首先得到当前结点的左子树和右子树的深度,然后计算以当前结点为根结点的二叉树的深度和最长路径长度,并维护二叉树的直径。遍历结束之后,即可得到二叉树的直径。
代码
class Solution {int diameter = 0;public int diameterOfBinaryTree(TreeNode root) {getDepth(root);return diameter;}public int getDepth(TreeNode node) {if (node == null) {return 0;}int leftDepth = getDepth(node.left);int rightDepth = getDepth(node.right);diameter = Math.max(diameter, leftDepth + rightDepth);return Math.max(leftDepth, rightDepth) + 1;}
}
复杂度分析
-
时间复杂度: O ( n ) O(n) O(n),其中 n n n 是二叉树的结点数。每个结点都被访问一次。
-
空间复杂度: O ( n ) O(n) O(n),其中 n n n 是二叉树的结点数。空间复杂度主要是递归调用的栈空间,取决于二叉树的高度,最坏情况下是 O ( n ) O(n) O(n)。
相关文章:

二叉树题目:二叉树的直径
文章目录 题目标题和出处难度题目描述要求示例数据范围 解法思路和算法代码复杂度分析 题目 标题和出处 标题:二叉树的直径 出处:543. 二叉树的直径 难度 3 级 题目描述 要求 给定二叉树的根结点 root \texttt{root} root,返回其直径…...
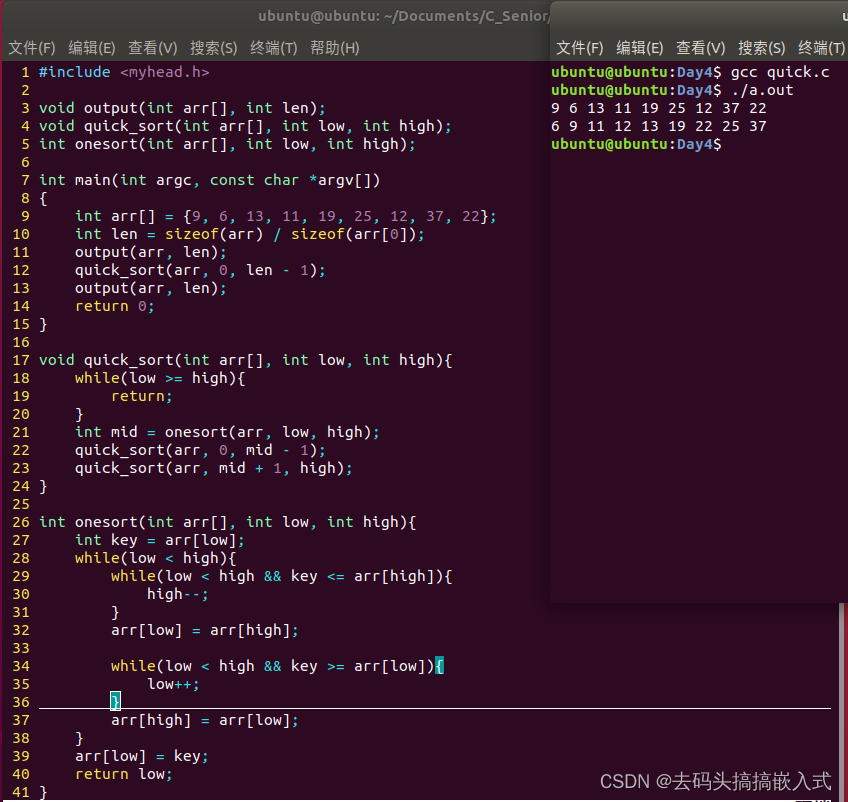
嵌入式:C高级 Day4
一、整理思维导图 二、写一个函数,获取用户的uid和gid并使用变量接收 三、整理冒泡排序、简单选择排序和快速排序的代码 冒泡排序 #include <myhead.h>void output(int arr[], int len); void bubble_sort(int arr[], int len);int main(int argc, const ch…...
——函数相关)
cmake常用命令(1)——函数相关
一、function/endfunction cmake中的函数与其他语言相似,表示一个命令集,可以被重复调用。形式如下: function(<name> [<arg1> ...])<commands> endfunction() function:表示函数开始 <name>…...

阿里三年功能测试的一些感悟
一、前言 功能测试是测试工程师的基础功,很多人功能测试还做不好,就想去做性能测试、自动化测试。很多人对功能测试的理解就是点点点,如何自己不用心去悟,去研究,那么你的职业生涯也就停留在点点点上了。在这里&#…...

React源码解析18(4)------ completeWork的工作流程【mount】
摘要 经过上一章,我们得到的FilberNode已经具有了child和return属性。一颗Filber树的结构已经展现出来了。 那我们最终是想在页面渲染真实的DOM。所以我们现在要在completeWork里,构建出一颗离屏的DOM树。 之前在说FilberNode的属性时,我们…...

Kafka: 详解、使用教程和示例
Kafka: 详细介绍、使用教程和示例 什么是 Kafka? Kafka 是一个分布式的流处理平台,最初由 LinkedIn 开发,现已成为 Apache 基金会的顶级项目。它以高吞吐量、可靠性和可扩展性而闻名,被广泛应用于实时数据传输、日志收集、事件处…...
【LeetCode周赛】LeetCode第358场周赛
LeetCode第358场周赛 数组中的最大数对和翻倍以链表形式表示的数字限制条件下元素之间的最小绝对差 数组中的最大数对和 给你一个下标从0开始的整数数组nums。请你从nums中找出和最大的一对数,且这两个数数位上最大的数字相等。 返回最大和,如果不存在满…...
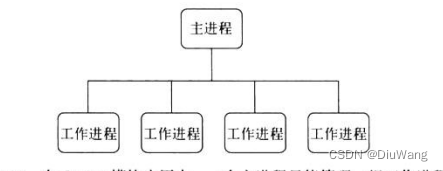
Node.js学习笔记-04
这第九章也是个大重点 九、玩转进程 Node在选型时决定在V8引擎之上构建,也就意味着它的模型与浏览器类似。 本章关于进程的介绍和讨论将会解决如下两个问题: 单进程单线程并非完美,如今CPU基本均是多核的,真正的服务器…...
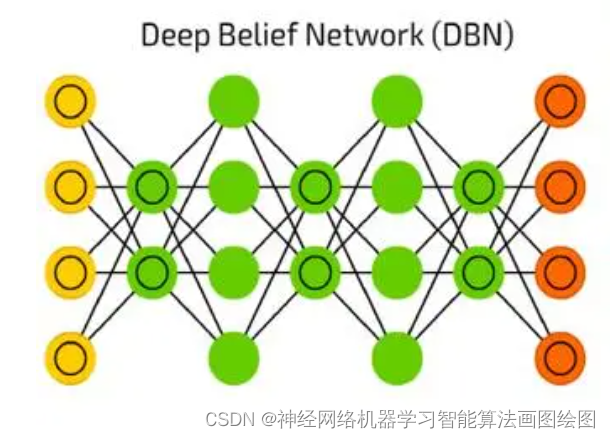
基于dbn+svr的交通流量预测,dbn详细原理
目录 背影 DBN神经网络的原理 DBN神经网络的定义 受限玻尔兹曼机(RBM) DBN+SVR的交通流量预测 基本结构 主要参数 数据 MATALB代码 结果图 展望 背影 DBN是一种深度学习神经网络,拥有提取特征,非监督学习的能力,是一种非常好的分类算法,本文将DBN+SVR用于交通流量预测…...
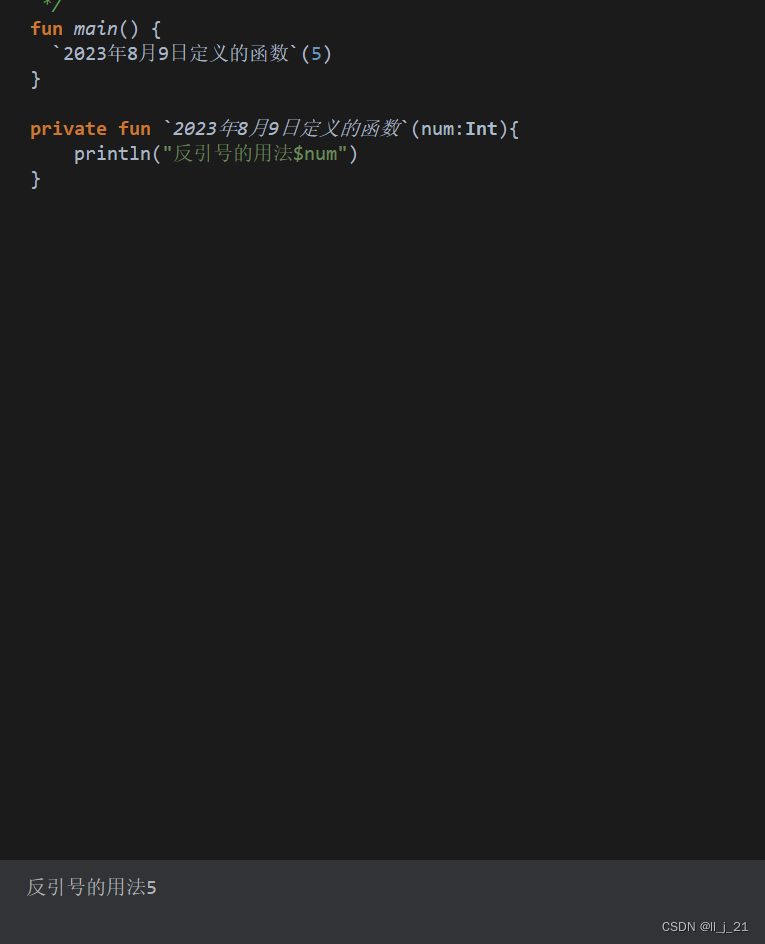
【第一阶段】kotlin中反引号中的函数名特点
在kotlin中可以直接中文定义函数,使用反引号进行调用 eg: fun main() {2023年8月9日定义的函数(5) }private fun 2023年8月9日定义的函数(num:Int){println("反引号的用法$num") }执行结果 在Java中is,in可以定义方法,但是在kotlin中is,in是…...
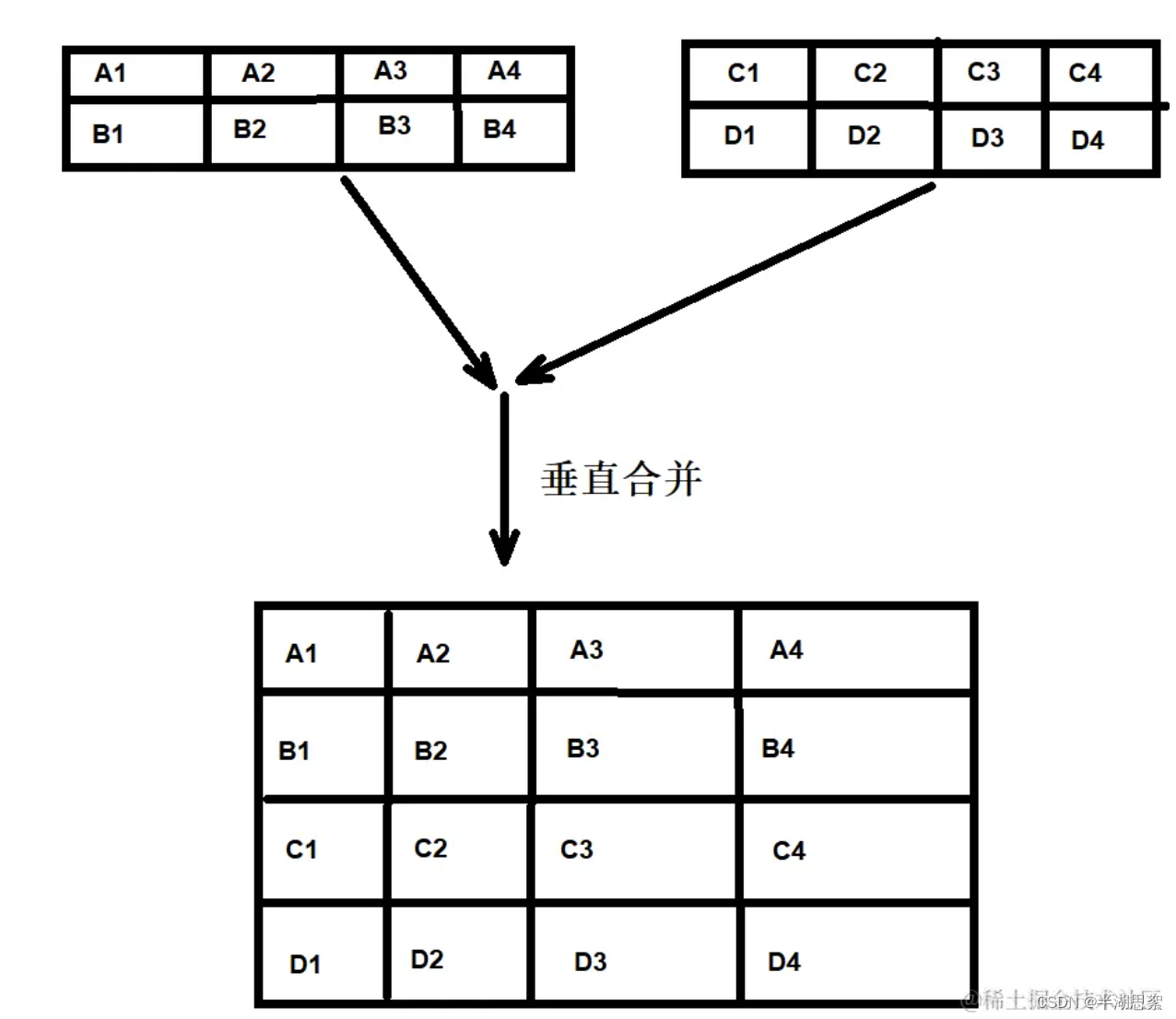
数据分析-python学习 (1)numpy相关
内容为:https://juejin.cn/book/7240731597035864121的学习笔记 导包 import numpy as np numpy数组创建 创建全0数组,正态分布、随机数组等就不说了,提供了相应的方法通过已有数据创建有两种 arr1np.array([1,2,3,4,5]) 或者datanp.loadt…...

数据库的游标
数据库的游标(Cursor)是用于在数据库中进行数据操作的一个控制结构。它类似于在编程语言中使用的指针或迭代器,用于遍历数据库结果集并在结果集上执行各种操作。 游标允许我们在数据库查询的结果集中逐行移动,并对每一行执行特定…...
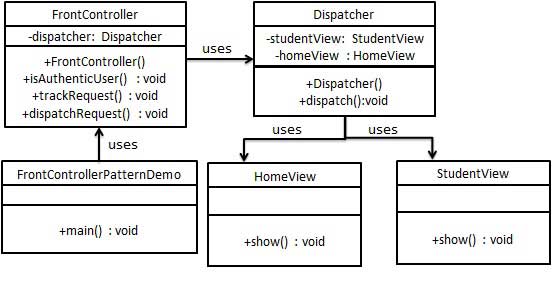
【设计模式】前端控制器模式
前端控制器模式(Front Controller Pattern)是用来提供一个集中的请求处理机制,所有的请求都将由一个单一的处理程序处理。该处理程序可以做认证/授权/记录日志,或者跟踪请求,然后把请求传给相应的处理程序。以下是这种…...

SQL | 过滤数据
4-过滤数据 4.1-使用WHERE子句 数据根据 WHERE 子句中指定的搜索条件进行过滤。WHERE 子句在表名( FROM 子句)之后给出。 select prod_name,prod_price from products where prod_price 3.49; 上述语句查询价格为3.49的行,然后输出名字和…...
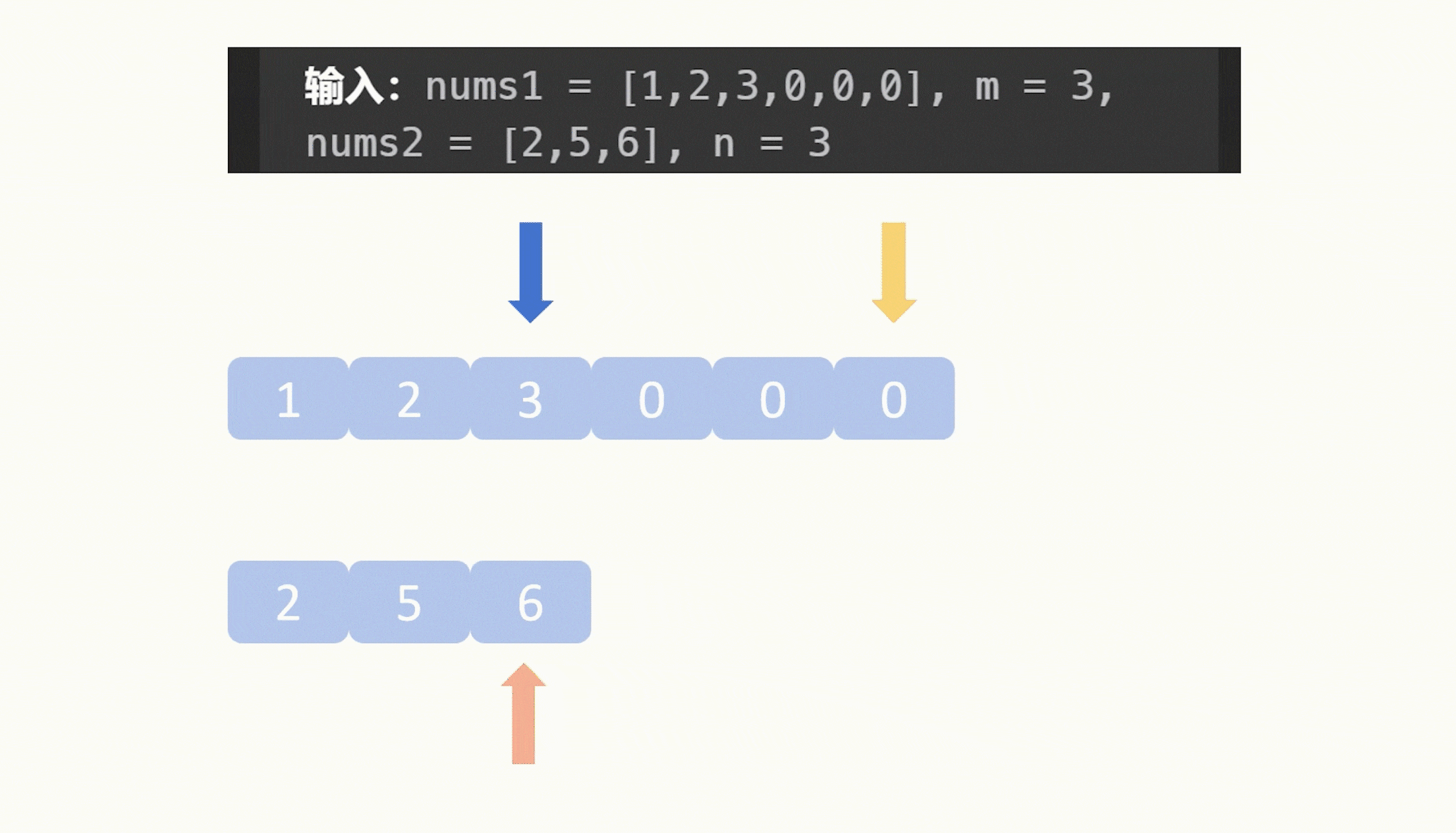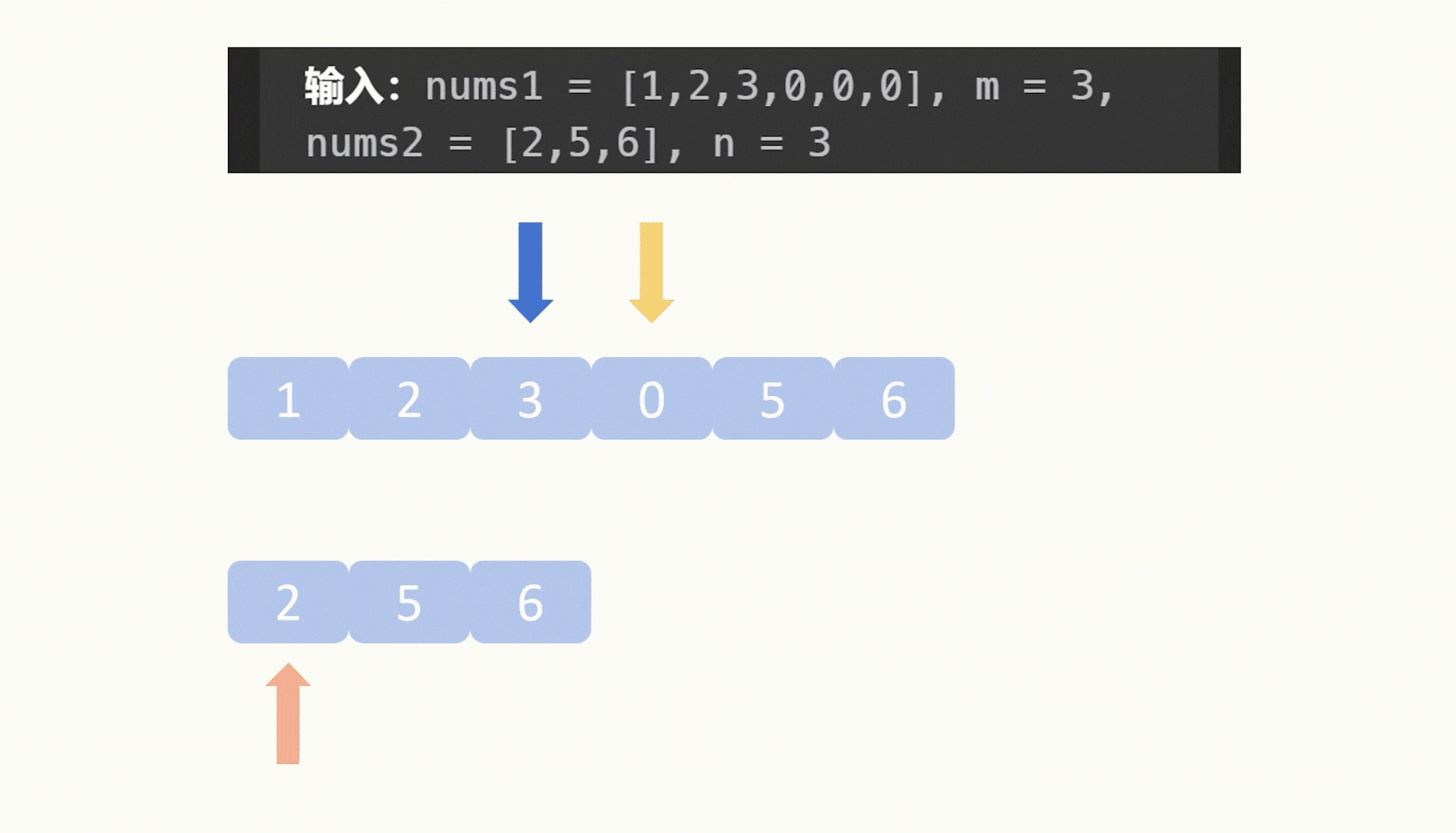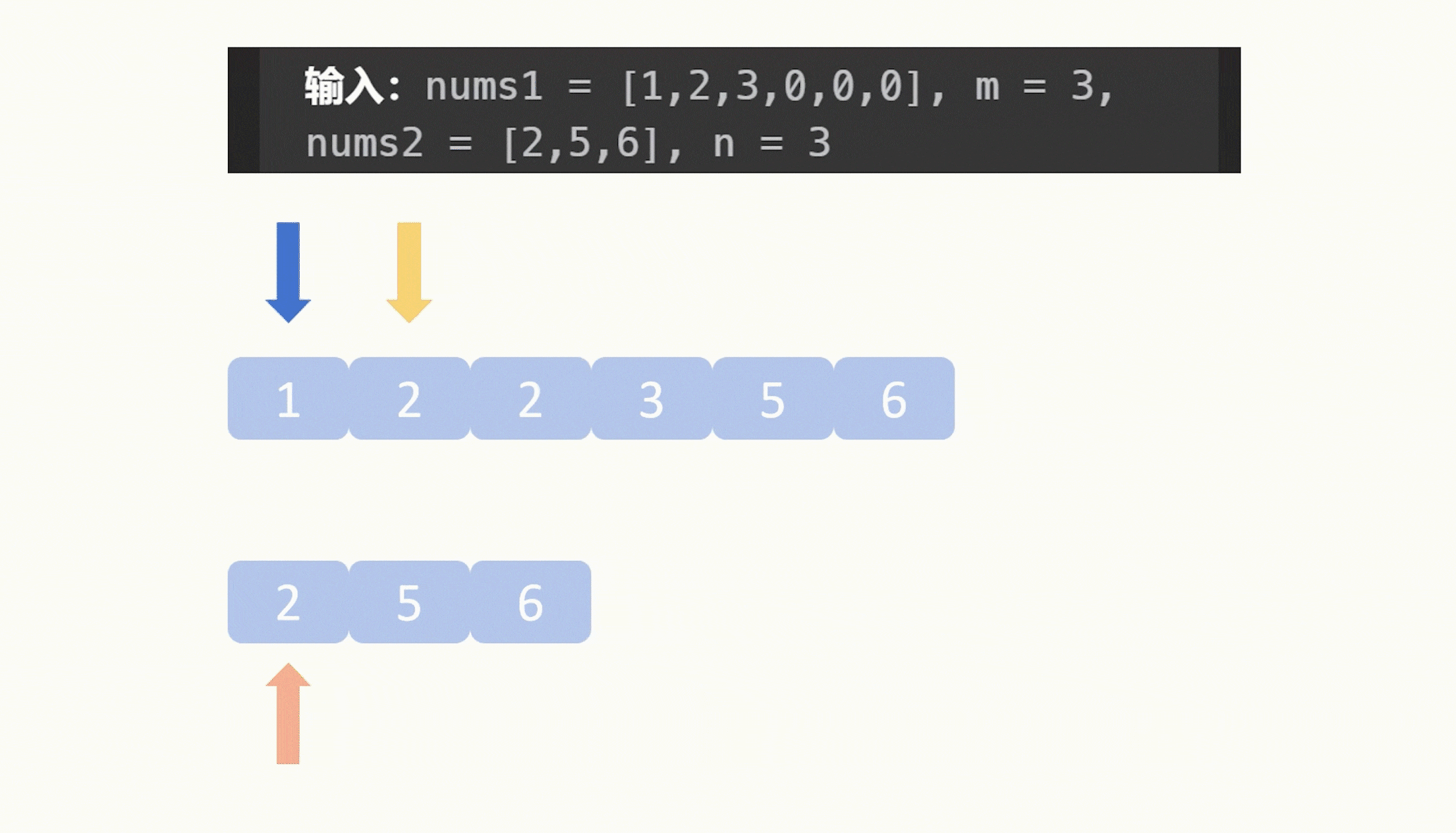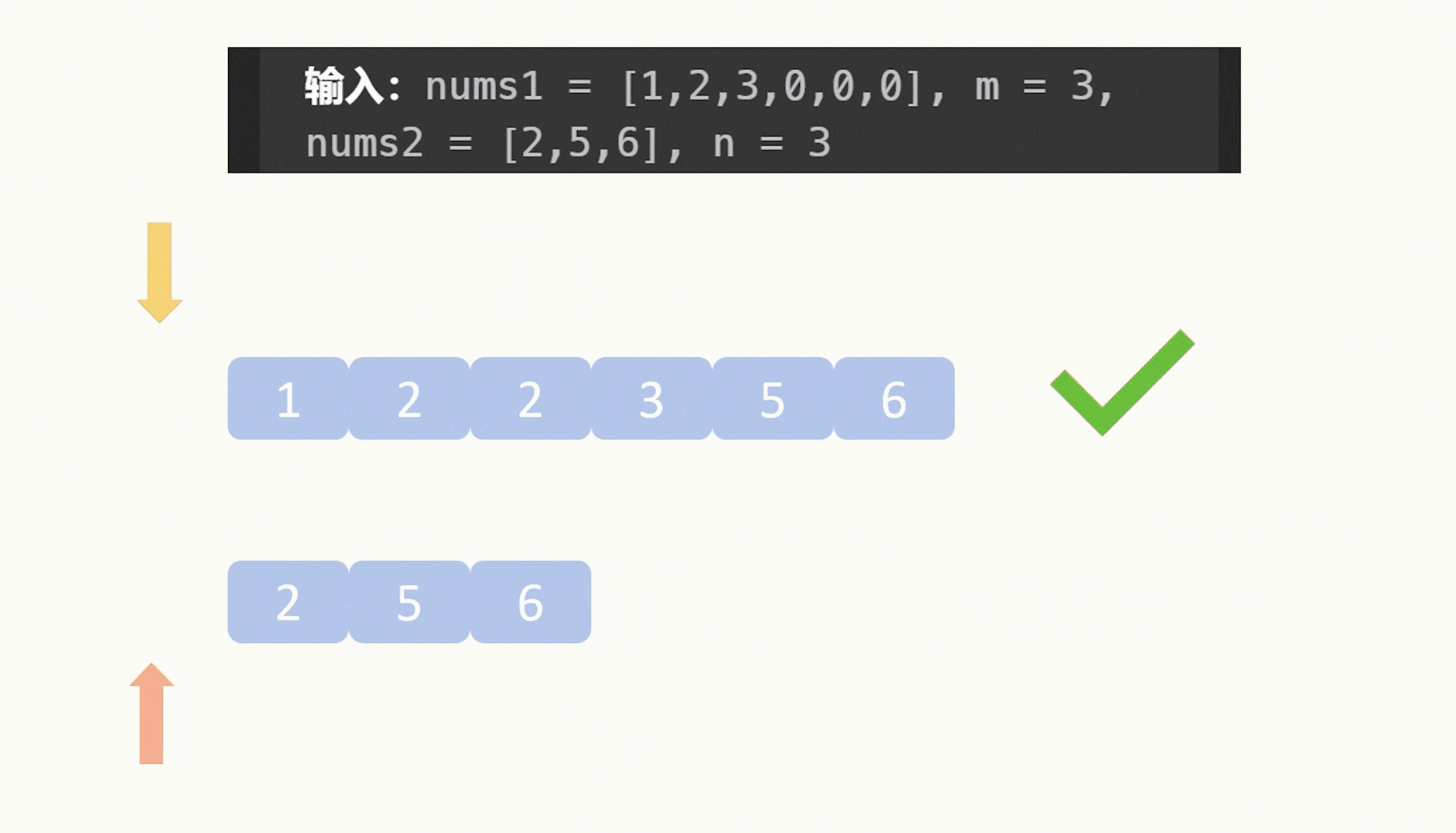
【力扣每日一题】2023.8.13 合并两个有序数组
目录 题目: 示例: 分析: 代码: 题目: 示例: 分析: 题目给我们两个升序数组,让我们合并它们,要求合并之后仍然是升序,并且这个合并操作是在数组1原地修改…...
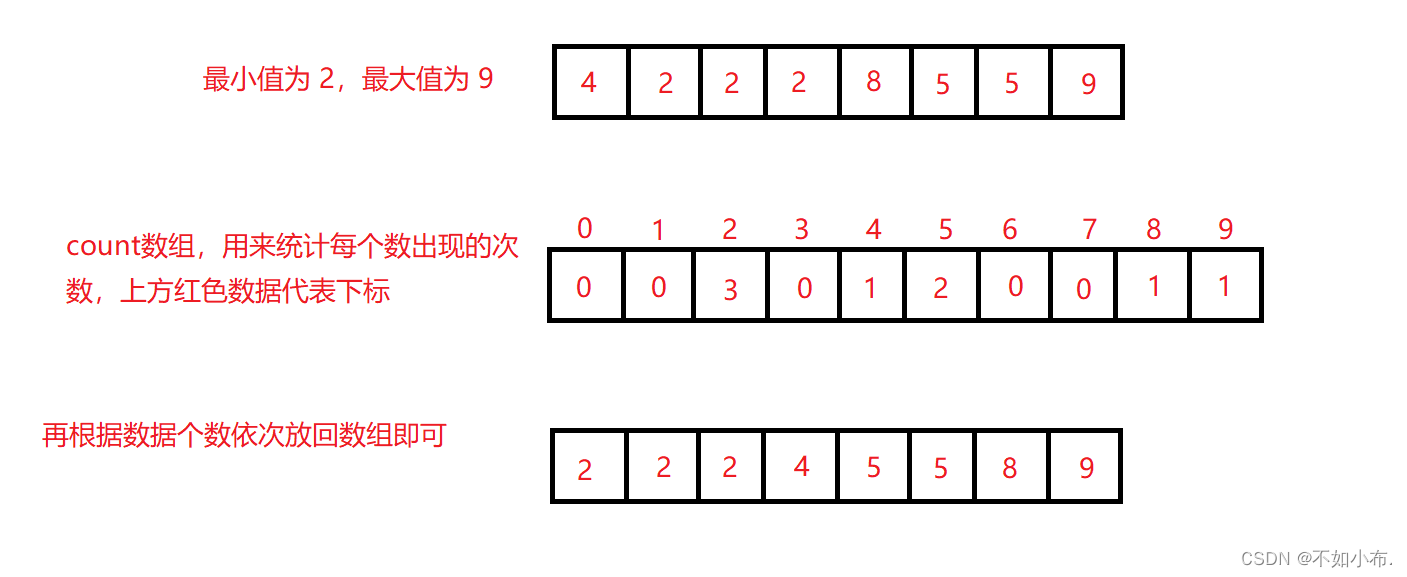
数据结构篇七:排序
文章目录 前言1.插入排序1.1 基本思想1.2 代码实现1.3 特性总结 2.希尔排序2.1 基本思想2.2 代码实现2.3 特性总结 3. 选择排序3.1 基本思想3.2 代码实现3.3 特性总结 4. 堆排序4.1 基本思想4.2 代码实现4.3 特性总结 5. 冒泡排序5.1 基本思想5.2 代码实现5.3 特性总结 6. 快速…...

Vue组件的边界情况
01.$root; 访问组件的根实例;用的不多,基本上在vuex上进行数据操作; 02.$parent/$children; 可以获得父组件或者子组件上边的数据;一般不建议使用$parent,因为如果获取这个值进行修改的话,也会更改父组件上…...

less、sass的使用及其区别
CSS预处理器 CSS 预处理器是一种扩展了原生 CSS 的工具,它们添加了一些编程语言的特性,以便更有效地编写、组织和维护样式代码。预处理器允许开发者使用变量、嵌套、函数、混合等功能,从而使 CSS 更具可读性、可维护性和重用性,特…...
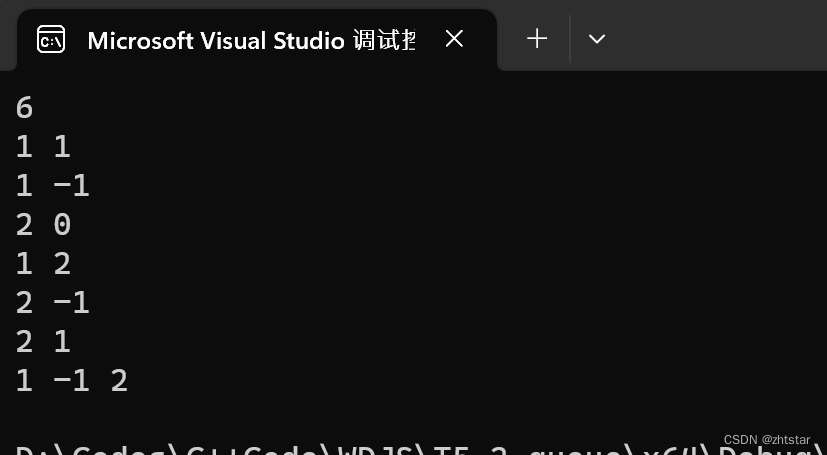
[保研/考研机试] 猫狗收容所 C++实现
题目描述: 输入: 第一个是n,它代表操作序列的次数。接下来是n行,每行有两个值m和t,分别代表题目中操作的两个元素。 输出: 按顺序输出收养动物的序列,编号之间以空格间隔。 源代码ÿ…...

Kotlin 基础教程一
Kotlin 基本数据类型 Java | Kotlin byte Byte short Short int Int long Long float Float double Double boolean Boolean c…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...
