【LeetCode周赛】LeetCode第358场周赛
LeetCode第358场周赛
- 数组中的最大数对和
- 翻倍以链表形式表示的数字
- 限制条件下元素之间的最小绝对差
数组中的最大数对和
给你一个下标从0开始的整数数组nums。请你从nums中找出和最大的一对数,且这两个数数位上最大的数字相等。
返回最大和,如果不存在满足题意的数字对,返回 -1 。
示例 1:
输入:nums = [51,71,17,24,42] 输出:88 解释: i = 1 和 j = 2 ,nums[i] 和 nums[j]
数位上最大的数字相等,且这一对的总和 71 + 17 = 88 。 i = 3 和 j = 4 ,nums[i] 和 nums[j]
数位上最大的数字相等,且这一对的总和 24 + 42 = 66 。 可以证明不存在其他数对满足数位上最大的数字相等,所以答案是 88 。
示例 2:
输入:nums = [1,2,3,4]
输出:-1
解释:不存在数对满足数位上最大的数字相等。
提示:
2 <= nums.length <= 100
1 <= nums[i] <= 104
思路:
首先根据nums.length可以知道数据范围并不大,因此我们可以直接暴力枚举整数数组nums中的两个数,判断这两个数数位上最大的数字是否相等。维护一个maxx用于存储最大和,若满足条件,即这两个数数位上最大的数字相等,则更新maxx。
代码:
class Solution {
public:int maxSum(vector<int>& nums) {int maxx=-1;for(int i=0;i<nums.size();i++){for(int j=i+1;j<nums.size();j++){int ma1=0,ma2=0,tmp1=nums[i],tmp2=nums[j];while(tmp1){ma1=max(ma1,tmp1%10);tmp1/=10;}while(tmp2){ma2=max(ma2,tmp2%10);tmp2/=10;}if(ma1==ma2)maxx=max(maxx,nums[i]+nums[j]);}}return maxx;}
};
翻倍以链表形式表示的数字
给你一个 非空 链表的头节点 head ,表示一个不含前导零的非负数整数。
将链表 翻倍 后,返回头节点 head 。
示例 1:

输入:head = [1,8,9]
输出:[3,7,8]
解释:上图中给出的链表,表示数字 189 。返回的链表表示数字 189 * 2 = 378 。
示例 2:
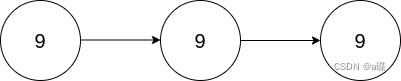
输入:head = [9,9,9]
输出:[1,9,9,8]
解释:上图中给出的链表,表示数字 999 。返回的链表表示数字 999 * 2 = 1998 。
提示:
链表中节点的数目在范围 [ 1 , 1 0 4 ] [1, 10^4] [1,104] 内
0 < = N o d e . v a l < = 9 0 <= Node.val <= 9 0<=Node.val<=9
生成的输入满足:链表表示一个不含前导零的数字,除了数字 0 本身。
思路:
这道题主要考察的是对链表的操作,既然要对链表翻倍,那么我们一定要考虑到进位如何表示,可以先将链表进行翻转,翻转之后对链表的各个数字进行翻倍的操作会变得简单一些。最后再将链表翻转回来即可。
代码:
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode *reverse(ListNode *p){ListNode *q=NULL;while(p){//链表翻转ListNode *x=(ListNode*)malloc(sizeof(ListNode));x->val=p->val;if(q==NULL){q=x;q->next=NULL;}else{x->next=q;q=x;}p=p->next;}return q;}ListNode* doubleIt(ListNode* head) {int num=0;ListNode *p,*x,*q;p=head;q=reverse(p);ListNode *h=q;int pre=0;while(q){//将链表进行翻倍int k=q->val;k*=2;q->val=k%10+pre;pre=k/10;//加在下一位上q=q->next;}h=reverse(h);if(pre){//如果最高位也需要进位x=(ListNode*)malloc(sizeof(ListNode));x->val=pre;x->next=NULL;x->next=h;h=x;}return h;}
};
限制条件下元素之间的最小绝对差
给你一个下标从 0 开始的整数数组 nums 和一个整数 x 。
请你找到数组中下标距离至少为 x 的两个元素的 差值绝对值 的 最小值 。
换言之,请你找到两个下标 i 和 j ,满足 abs(i - j) >= x 且 abs(nums[i] - nums[j]) 的值最小。
请你返回一个整数,表示下标距离至少为 x 的两个元素之间的差值绝对值的 最小值 。
示例 1:
输入:nums = [4,3,2,4], x = 2
输出:0 解释:我们选择 nums[0] = 4 和 nums[3] = 4 。
它们下标距离满足至少为 2 ,差值绝对值为最小值 0 。 0 是最优解。
示例 2:
输入:nums = [5,3,2,10,15], x = 1
输出:1
解释:我们选择 nums[1] = 3 和 nums[2] = 2 。 它们下标距离满足至少为 1 ,差值绝对值为最小值 1 。 1 是最优解。
示例 3:
输入:nums = [1,2,3,4], x = 3
输出:3
解释:我们选择 nums[0] = 1 和 nums[3] = 4 。它们下标距离满足至少为 3 ,差值绝对值为最小值 3 。 3 是最优解。
提示:
1 < = n u m s . l e n g t h < = 1 0 5 1 <= nums.length <= 10^5 1<=nums.length<=105
1 < = n u m s [ i ] < = 1 0 9 1 <= nums[i] <= 10^9 1<=nums[i]<=109
0 < = x < n u m s . l e n g t h 0 <= x < nums.length 0<=x<nums.length
思路:
看到数据范围,知道暴力枚举方法必定会时间超限,看到两个下标,我第一眼想到的就是双指针,滑动窗口的方法。当我们处理第i个数的时候,如果i+x以及之后的数是有序的,那么我们可以通过二分很快计算出最接近与nums[i]的数。
如何维护这个有序的序列呢。数据结构set可以保证集合的有序,使用multiset可以保证序列中存在重复的数字。
所以我们初始化一个multiset,命名ms,一开始将从x位置往后的所有数字都插入ms中。从下标为0的位置i开始逐一枚举,找到和其下标距离大于等于x且与其最相近的一个数,可以使用lower_bound找到第一个大于等于该数的数a。但是与此同时,我们还需要考虑这个数字a的前一个数字(即小于该数的最大的数),计算这两个数和nums[i]的差值,维护最小值即可。
然后开始移动窗口,往右移动一格,则第i+x的数需要移出,因为距离小于x了。然后还需要将i+1-x位置的数移入,因为该位置距离为x。
代码:
class Solution {
public:int minAbsoluteDifference(vector<int>& nums, int x) {if(x==0)return 0;multiset<int>ms;//用来维护一个有序的集合int n=nums.size();for(int i=x;i<n;i++)ms.insert(nums[i]);int ans=1e9;for(int i=0;i<n;i++){auto it=ms.lower_bound(nums[i]);//找到后面的大于等于nums[i]的最小的数字if(it!=ms.end())ans=min(ans,*it-nums[i]);if(it!=ms.begin())ans=min(ans,nums[i]-*prev(it));//找到该数字的前一个数字//移动窗口if(i+x<n)ms.erase(ms.find(nums[i+x]));//往后移动,移除if(i+1-x>=0)ms.insert(nums[i+1-x]);//这个位置的数也符合要求了}return ans;}
};
相关文章:

【LeetCode周赛】LeetCode第358场周赛
LeetCode第358场周赛 数组中的最大数对和翻倍以链表形式表示的数字限制条件下元素之间的最小绝对差 数组中的最大数对和 给你一个下标从0开始的整数数组nums。请你从nums中找出和最大的一对数,且这两个数数位上最大的数字相等。 返回最大和,如果不存在满…...
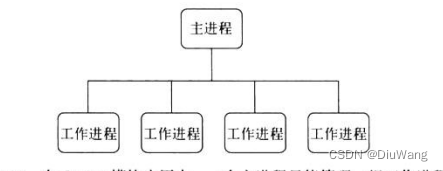
Node.js学习笔记-04
这第九章也是个大重点 九、玩转进程 Node在选型时决定在V8引擎之上构建,也就意味着它的模型与浏览器类似。 本章关于进程的介绍和讨论将会解决如下两个问题: 单进程单线程并非完美,如今CPU基本均是多核的,真正的服务器…...
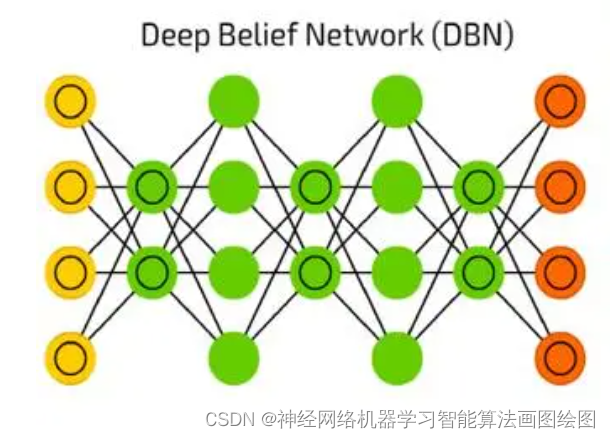
基于dbn+svr的交通流量预测,dbn详细原理
目录 背影 DBN神经网络的原理 DBN神经网络的定义 受限玻尔兹曼机(RBM) DBN+SVR的交通流量预测 基本结构 主要参数 数据 MATALB代码 结果图 展望 背影 DBN是一种深度学习神经网络,拥有提取特征,非监督学习的能力,是一种非常好的分类算法,本文将DBN+SVR用于交通流量预测…...
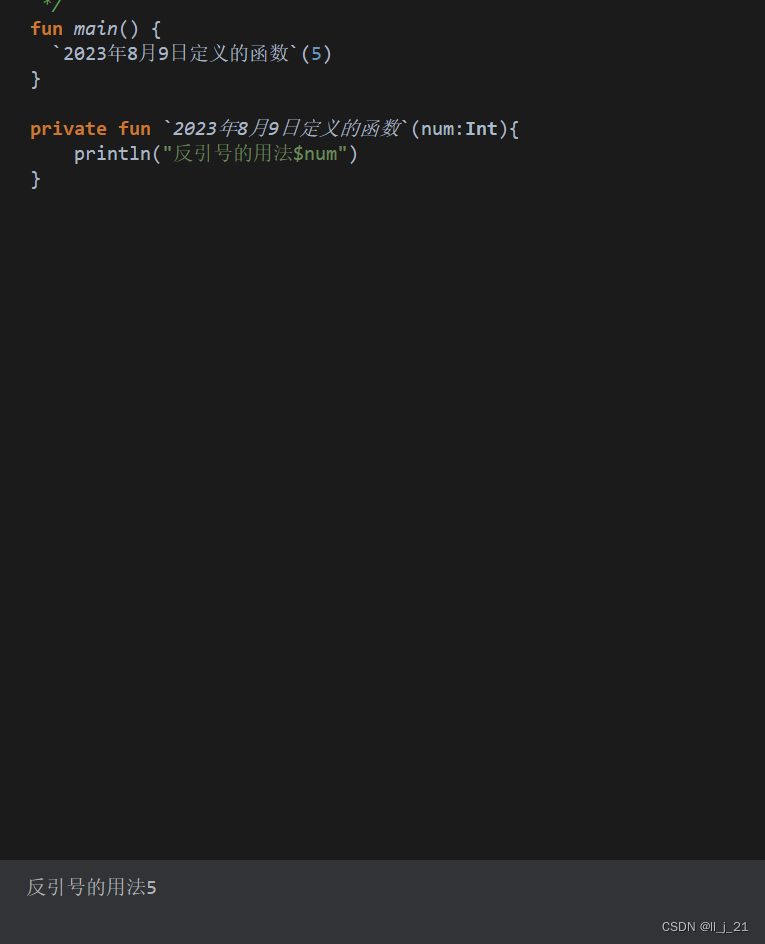
【第一阶段】kotlin中反引号中的函数名特点
在kotlin中可以直接中文定义函数,使用反引号进行调用 eg: fun main() {2023年8月9日定义的函数(5) }private fun 2023年8月9日定义的函数(num:Int){println("反引号的用法$num") }执行结果 在Java中is,in可以定义方法,但是在kotlin中is,in是…...
数据分析-python学习 (1)numpy相关
内容为:https://juejin.cn/book/7240731597035864121的学习笔记 导包 import numpy as np numpy数组创建 创建全0数组,正态分布、随机数组等就不说了,提供了相应的方法通过已有数据创建有两种 arr1np.array([1,2,3,4,5]) 或者datanp.loadt…...

数据库的游标
数据库的游标(Cursor)是用于在数据库中进行数据操作的一个控制结构。它类似于在编程语言中使用的指针或迭代器,用于遍历数据库结果集并在结果集上执行各种操作。 游标允许我们在数据库查询的结果集中逐行移动,并对每一行执行特定…...
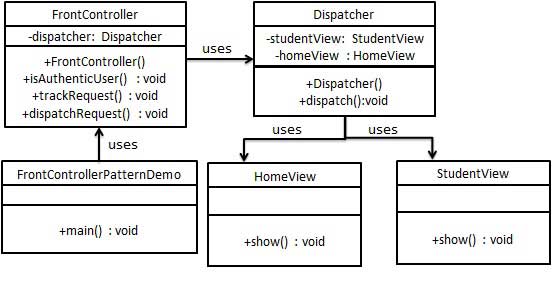
【设计模式】前端控制器模式
前端控制器模式(Front Controller Pattern)是用来提供一个集中的请求处理机制,所有的请求都将由一个单一的处理程序处理。该处理程序可以做认证/授权/记录日志,或者跟踪请求,然后把请求传给相应的处理程序。以下是这种…...

SQL | 过滤数据
4-过滤数据 4.1-使用WHERE子句 数据根据 WHERE 子句中指定的搜索条件进行过滤。WHERE 子句在表名( FROM 子句)之后给出。 select prod_name,prod_price from products where prod_price 3.49; 上述语句查询价格为3.49的行,然后输出名字和…...
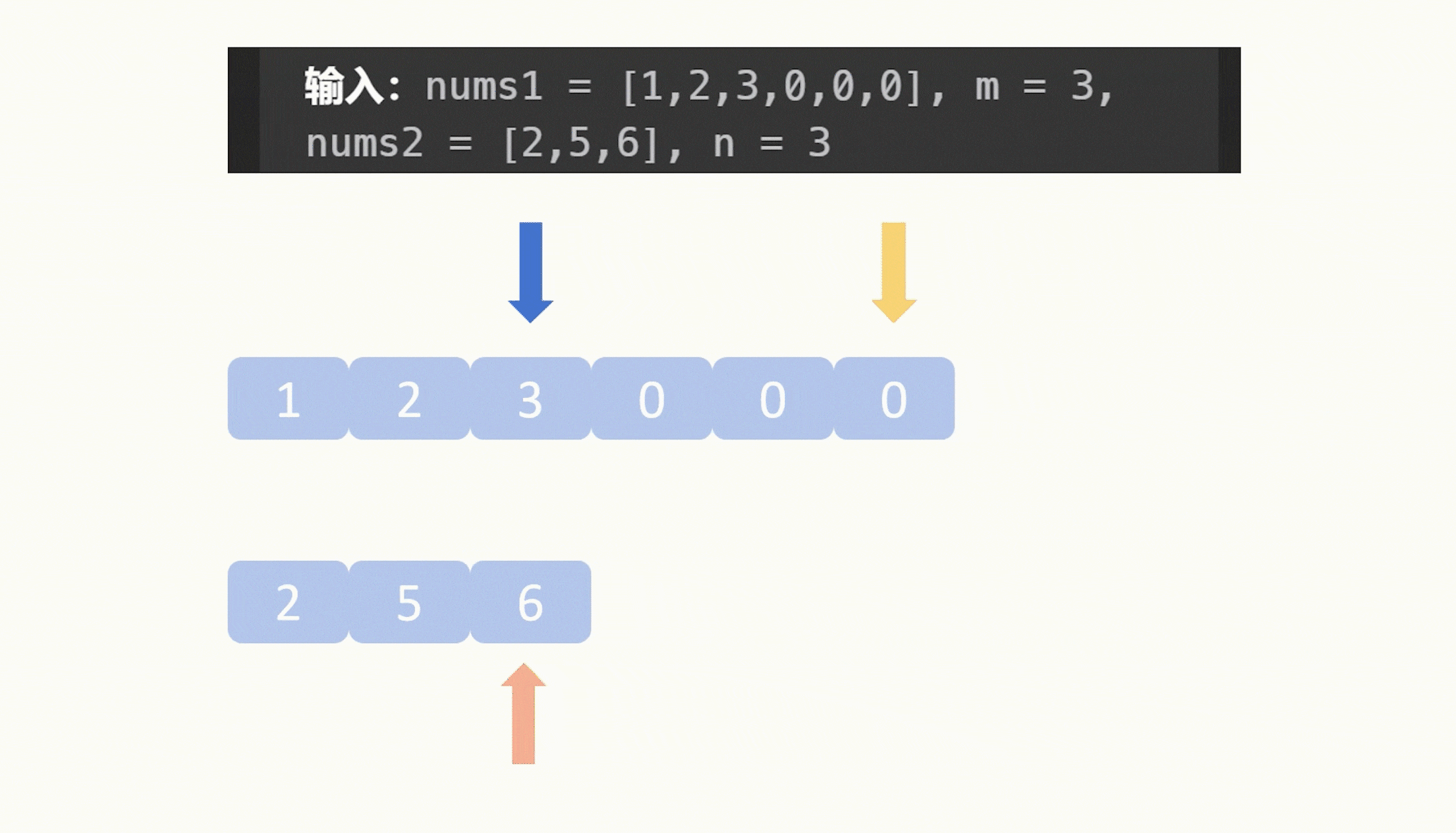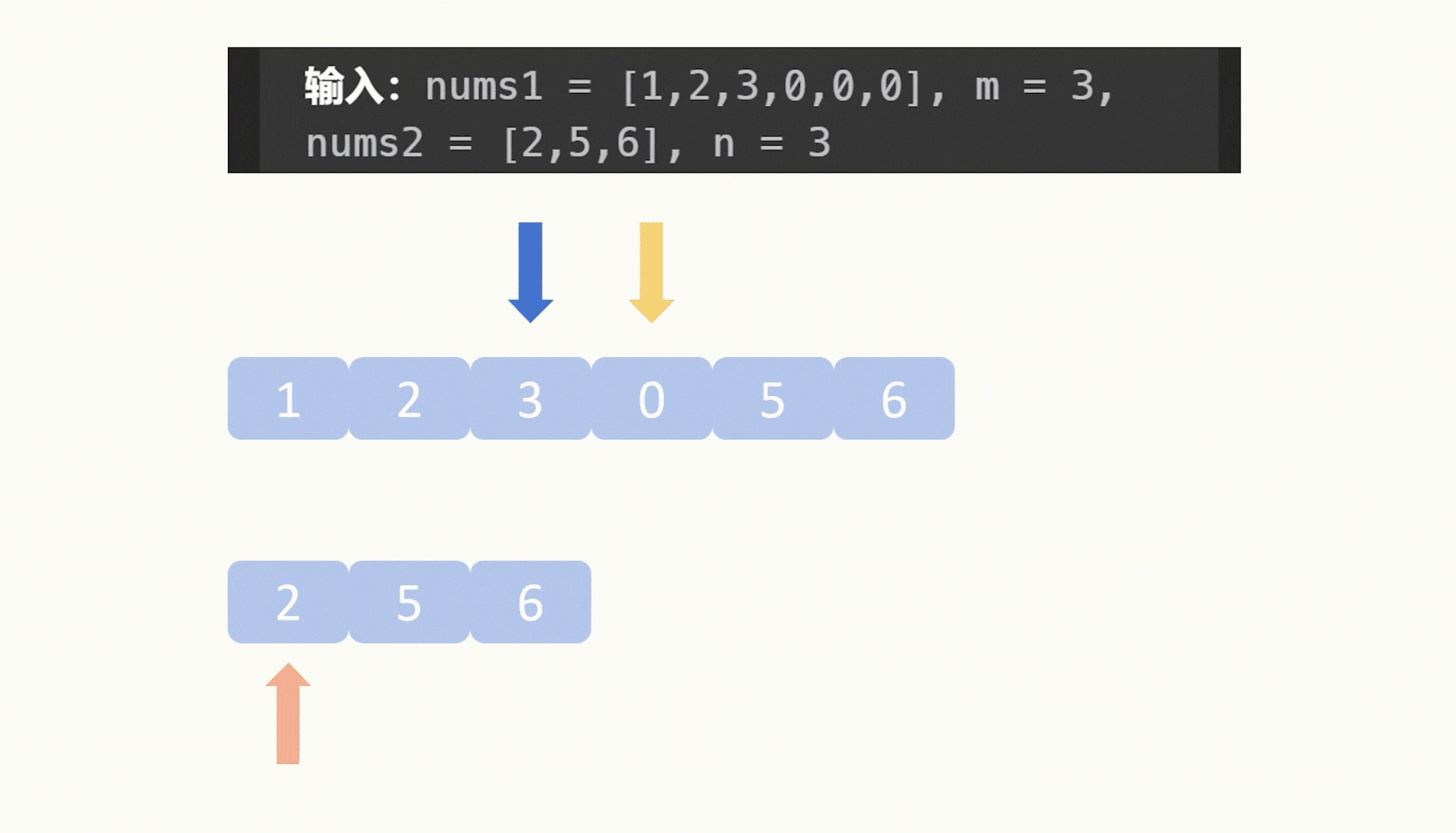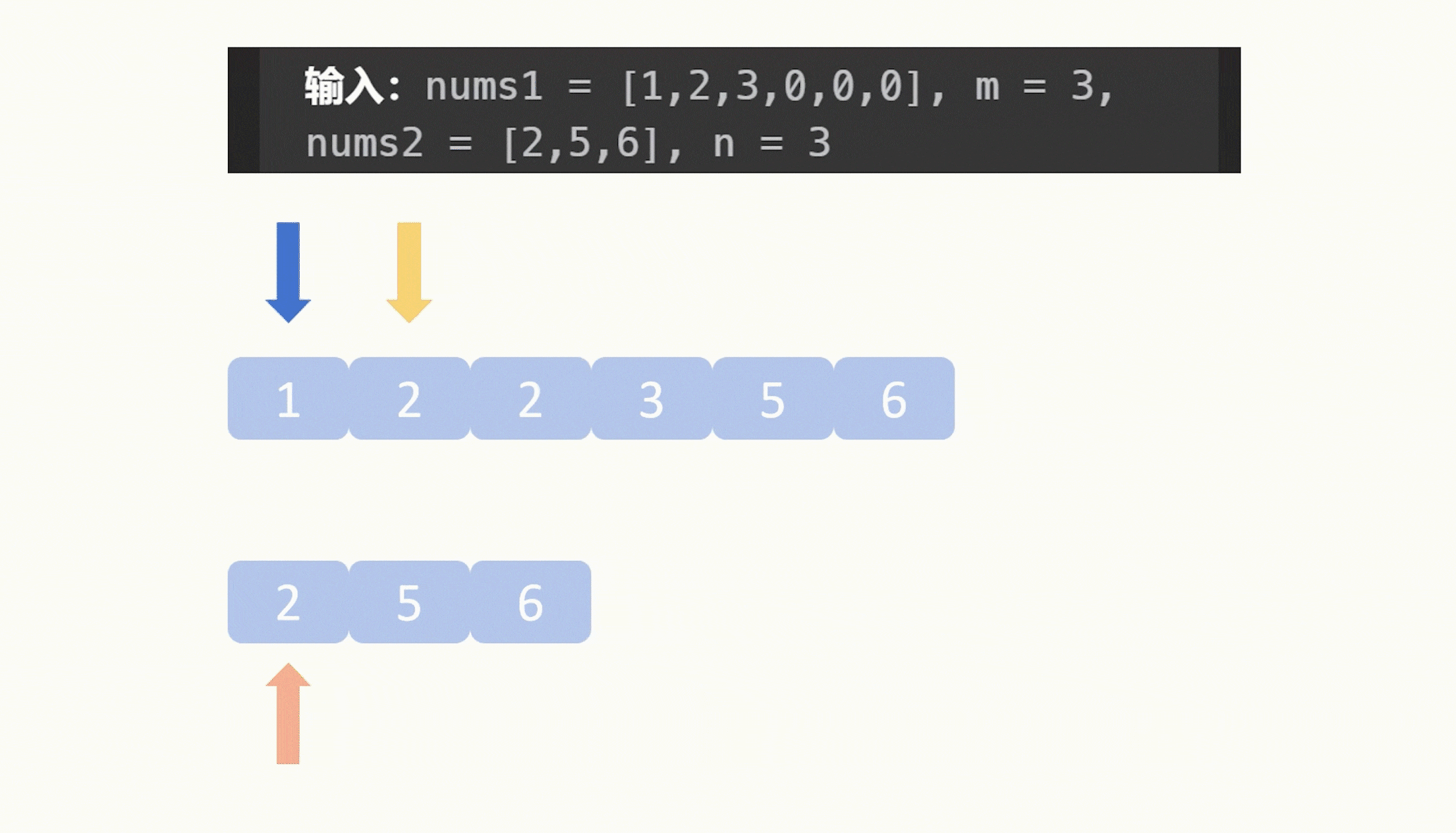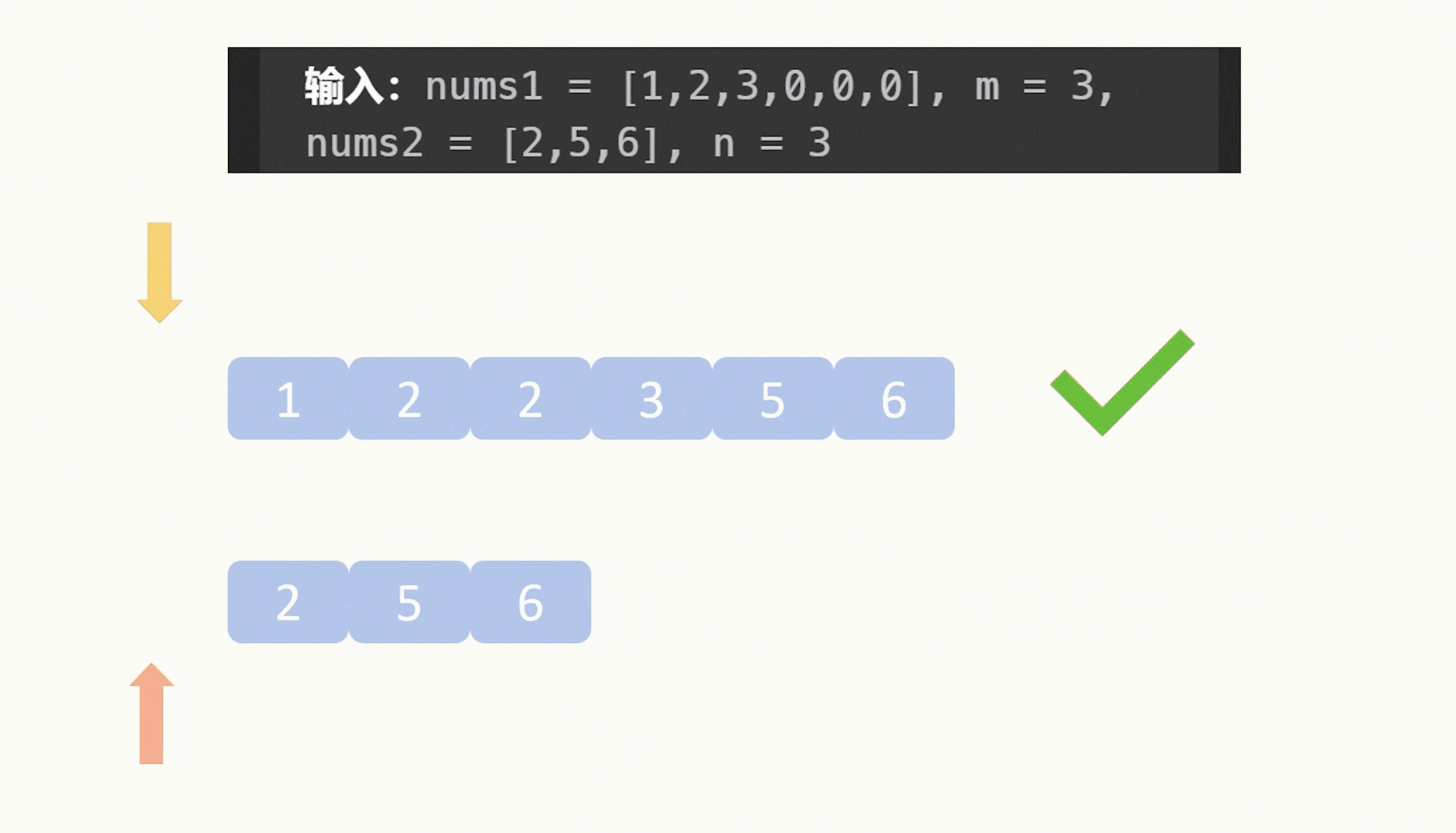
【力扣每日一题】2023.8.13 合并两个有序数组
目录 题目: 示例: 分析: 代码: 题目: 示例: 分析: 题目给我们两个升序数组,让我们合并它们,要求合并之后仍然是升序,并且这个合并操作是在数组1原地修改…...
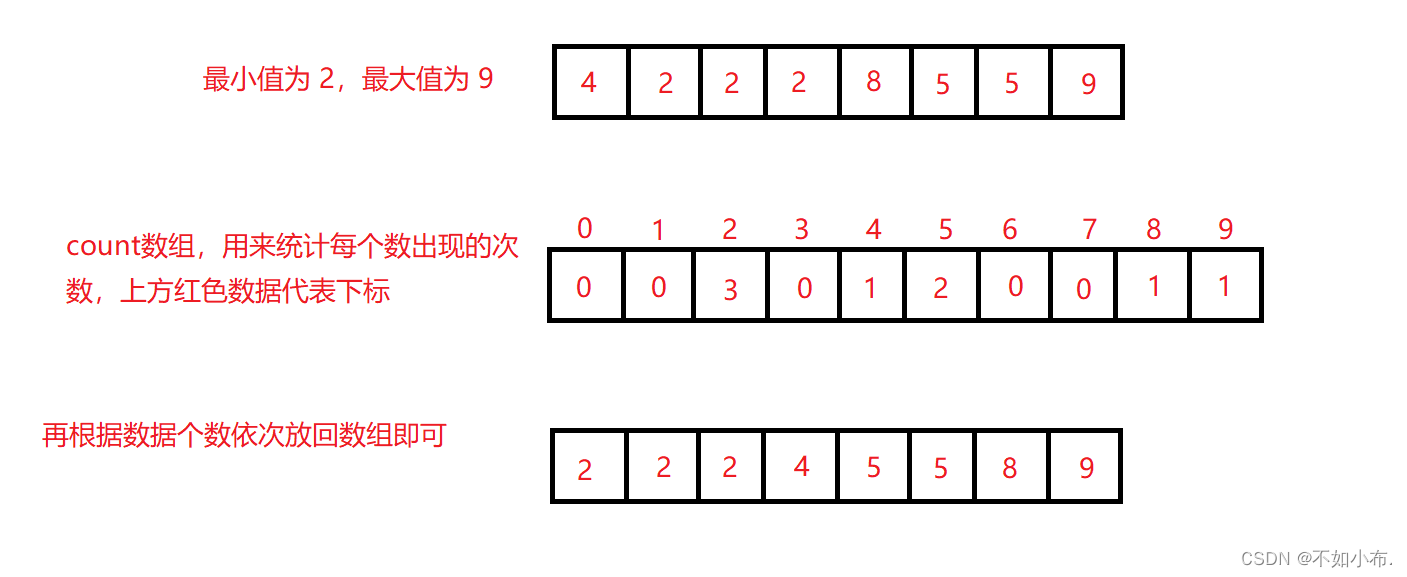
数据结构篇七:排序
文章目录 前言1.插入排序1.1 基本思想1.2 代码实现1.3 特性总结 2.希尔排序2.1 基本思想2.2 代码实现2.3 特性总结 3. 选择排序3.1 基本思想3.2 代码实现3.3 特性总结 4. 堆排序4.1 基本思想4.2 代码实现4.3 特性总结 5. 冒泡排序5.1 基本思想5.2 代码实现5.3 特性总结 6. 快速…...

Vue组件的边界情况
01.$root; 访问组件的根实例;用的不多,基本上在vuex上进行数据操作; 02.$parent/$children; 可以获得父组件或者子组件上边的数据;一般不建议使用$parent,因为如果获取这个值进行修改的话,也会更改父组件上…...

less、sass的使用及其区别
CSS预处理器 CSS 预处理器是一种扩展了原生 CSS 的工具,它们添加了一些编程语言的特性,以便更有效地编写、组织和维护样式代码。预处理器允许开发者使用变量、嵌套、函数、混合等功能,从而使 CSS 更具可读性、可维护性和重用性,特…...
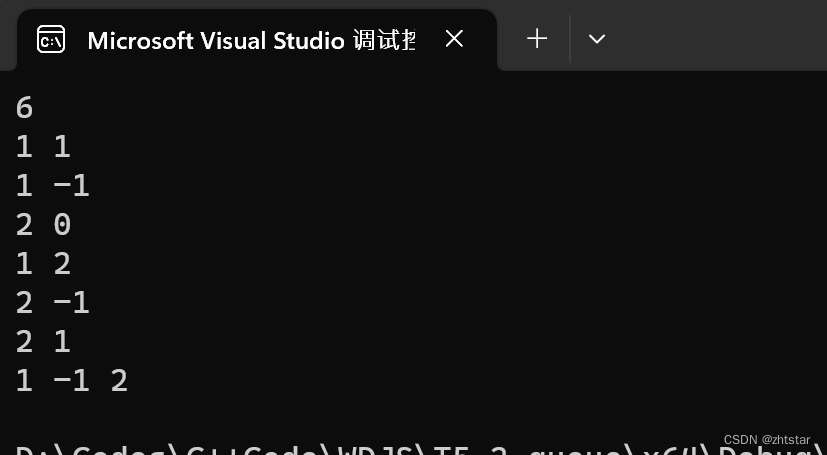
[保研/考研机试] 猫狗收容所 C++实现
题目描述: 输入: 第一个是n,它代表操作序列的次数。接下来是n行,每行有两个值m和t,分别代表题目中操作的两个元素。 输出: 按顺序输出收养动物的序列,编号之间以空格间隔。 源代码ÿ…...

Kotlin 基础教程一
Kotlin 基本数据类型 Java | Kotlin byte Byte short Short int Int long Long float Float double Double boolean Boolean c…...

数据结构笔记--前缀树的实现
1--前缀树的实现 前缀树的每一个节点拥有三个成员变量,pass表示有多少个字符串经过该节点,end表示有多少个字符串以该节点结尾,nexts表示该字符串可以走向哪些节点; #include <iostream> #include <unordered_map>str…...

C/C++时间获取函数
time.h包含C/C中用于获取时间,和时间转换方面的函数。 1、time() 函数 time_t time(time_t *seconds) 返回自(1970-01-01 00:00:00 UTC)起经过的时间,以秒为单位。如果 seconds 不为空,则返回值也存储在变量 seconds …...

sql中判断日期是否是同一天
sql中判断日期是否是同一天的sql sql: select id,product_id,seckill_price,stock_count,time,intergral,start_date from t_seckill_product where to_days(start_date) to_days(now()) to_days函数: 使用to_days(start_date) to_days(now())的方式是一种常见的…...
NAS搭建指南一——服务器的选择与搭建
一、服务器的选择 有自己的本地的公网 IP 的请跳过此篇文章按需求选择一个云服务器,目的就是为了进行 frp 的搭建,完成内网穿透我选择的是腾讯云服务器,我的配置如下,仅供参考: 4. 腾讯云服务器官网地址 二、服务器…...
豪越HYDO智能运维助力智慧医院信息化建设
随着国家政策的推动与支持,医疗行业信息化应用不断普及,大数据、AI、医疗物联网等技术的应用,快速推动了电子病历、智慧服务、智慧管理的智慧医院建设和医院信息标准化建设,通过不断探索创新“智慧医院”服务模式,实现…...

Week1题目重刷
今天把week1的题目都重新刷了一遍,明天开始week2的内容~ 704.二分查找 class Solution {public int search(int[] nums, int target) {int l 0, r nums.length - 1, m;while (l < r) {m (l r) >>> 1;if (nums[m] < target) {l m 1;} else if…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...
