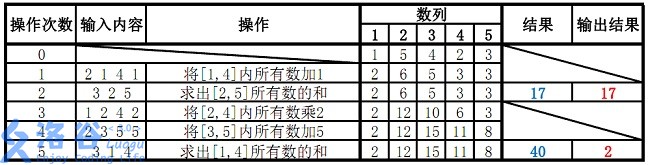
(二分查找) 11. 旋转数组的最小数字 ——【Leetcode每日一题】
❓剑指 Offer 11. 旋转数组的最小数字
难度:简单
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。
给你一个可能存在 重复 元素值的数组 numbers ,它原来是一个升序排列的数组,并按上述情形进行了一次旋转。请返回旋转数组的最小元素。例如,数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一次旋转,该数组的最小值为 1。
注意,数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。
示例 1:
输入:numbers = [3,4,5,1,2]
输出:1
示例 2:
输入:numbers = [2,2,2,0,1]
输出:0
提示:
n == numbers.length1 <= n <= 5000-5000 <= numbers[i] <= 5000numbers原来是一个升序排序的数组,并进行了1至n次旋转
注意:本题与 154. 寻找旋转排序数组中的最小值 II 相同。
💡思路:二分查找
将旋转数组对半分可以得到一个包含最小元素的新旋转数组,以及一个非递减排序的数组。新的旋转数组的长度是原数组的一半,从而将问题规模减少了一半,这种折半性质的算法的时间复杂度为 O ( l o g 2 N ) O(log2N) O(log2N)。
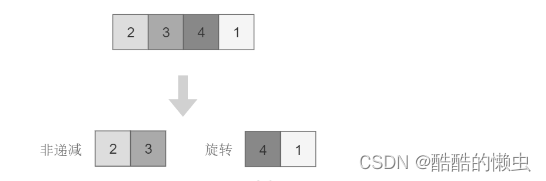
此时问题的关键在于确定对半分得到的两个数组哪一个是旋转数组,哪一个是非递减数组。我们很容易知道非递减数组的第一个元素一定小于等于最后一个元素。
通过修改二分查找算法进行求解(left、mid、right 分别代表包含最小元素的新旋转数组 左、中、右):
- 当
numbers[mid] > numbers[right]时,[left,mid]区间内的数组是非递减数组,[mid + 1, right]区间内的数组为新的旋转数组,此时,left = mid + 1; - 当
numbers[mid] < numbers[right]时,[mid,right]区间内的数组是非递减数组,[left, mid]区间内的数组为新的旋转数组,此时,right = mid; - 当
numbers[mid] = numbers[right]时, 无法判断哪一个是旋转数组,哪一个是非递减数组,此时right- -,直到能判断。
🍁代码:(C++、Java)
C++
class Solution {
public:int minArray(vector<int>& numbers) {int left = 0;int right = numbers.size() - 1;if(right == 0) return numbers[0];while(left < right){int mid = left + (right - left) / 2;if(numbers[mid] > numbers[right]){left = mid + 1;}else if(numbers[mid] < numbers[right]){right = mid;}else{right--;}}return numbers[left];}
};
Java
class Solution {public int minArray(int[] numbers) {int left = 0;int right = numbers.length - 1;if(right == 0) return numbers[0];while(left < right){int mid = left + (right - left) / 2;if(numbers[mid] > numbers[right]){left = mid + 1;}else if(numbers[mid] < numbers[right]){right = mid;}else{right--;}}return numbers[left];}
}
🚀 运行结果:
🕔 复杂度分析:
- 时间复杂度: O ( l o g n ) O(logn) O(logn),平均时间复杂度为 O ( l o g n ) O(logn) O(logn),其中
n是数组numbers的长度。如果数组是随机生成的,那么数组中包含相同元素的概率很低,在二分查找的过程中,大部分情况都会忽略一半的区间。而在最坏情况下,如果数组中的元素完全相同,那么while循环就需要执行n次,每次忽略区间的右端点,时间复杂度为O(n)。 - 空间复杂度: O ( 1 ) O(1) O(1)。
题目来源:力扣。
放弃一件事很容易,每天能坚持一件事一定很酷,一起每日一题吧!
关注我LeetCode主页 / CSDN—力扣专栏,每日更新!
注: 如有不足,欢迎指正!
相关文章:

(二分查找) 11. 旋转数组的最小数字 ——【Leetcode每日一题】
❓剑指 Offer 11. 旋转数组的最小数字 难度:简单 把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。 给你一个可能存在 重复 元素值的数组 numbers ,它原来是一个升序排列的数组,并按上述情形进行了一次旋转…...

docker 制作tomcat镜像
需要下载tomcat安装包和jdk安装包,我这边下载的jdk版本分别为(jdk和tomcat版本需要对应上) apache-tomcat-9.0.78.tar.gzjdk-8u381-linux-x64.tar.gz创建一个readme.txt空文件 readme.txt创建一个Dockerfile文件 # centos系统作为底层 FROM …...

年之年的选择,组装版
组件:<!--* Author: liuyu liuyuxizhengtech.com* Date: 2023-02-01 16:57:27* LastEditors: wangping wangpingxizhengtech.com* LastEditTime: 2023-06-30 17:25:14* Description: 时间选择年 - 年 --> <template><div class"year-range-pick…...

英语词法——代词
代词是用来代替名词、起名词作用的短语、分句和句子的词。英语中代词根据其意义和作用可分为九类:人称代词、物主代词、反身代词、相互代词、指示代词、疑问代词、不定代词、关系代词和连接代词。 第一节 人称代词 一、人称代词的形式和用法 人称代词单数复数第一人称第二人…...
1475.商品折扣后的最终价格
文章目录 题目描述解题思路:方法一:通俗解法方法二:单调栈 leetcode原题链接 1475. 商品折扣后的最终价格 题目描述 给你一个数组 prices ,其中 prices[i] 是商店里第 i 件商品的价格。 商店里正在进行促销活动,如果你…...

php、 go 语言怎么结合构建高性能高并发商城。
一、php、 go 语言怎么结合构建高性能高并发商城。 将PHP和Go语言结合起来构建高性能高并发的商城系统可以通过多种方法实现,以利用两种语言的优势。下面是一些可能的方法和策略: 1. **微服务架构:** 使用微服务架构,将系统拆分…...
ubuntu 部署 ChatGLM-6B 完整流程 模型量化 Nvidia
ubuntu 部署 ChatGLM-6B 完整流程 模型量化 Nvidia 初环境与设备环境准备克隆模型代码部署 ChatGLM-6B完整代码 ChatGLM-6B 是一个开源的、支持中英双语的对话语言模型,基于 General Language Model (GLM) 架构,具有 62 亿参数。结合模型量化技术&#x…...

【数据分享】2001-2022年我国省市县镇四级的逐月最高气温数据(无需转发/Shp/Excel格式)
气象数据是在各项研究中都非常常用的数据!之前我们分享过来自于国家青藏高原科学数据中心的1901-2022年1km分辨率的逐月平均气温栅格数据,以及基于该栅格数据处理的Shp和Excel格式的2001-2022年我国省市县镇四级的逐月平均气温数据(可查看之前…...
线段树-模板-区间查询-区间修改
【模板】线段树 2 传送门:https://www.luogu.com.cn/problem/P3373 题单:https://www.luogu.com.cn/training/16376#problems 题目描述 如题,已知一个数列,你需要进行下面三种操作: 将某区间每一个数乘上 x x x&a…...

微服务架构和分布式架构的区别
微服务架构和分布式架构的区别 有:1、含义不同;2、概念层面不同;3、解决问题不同;4、部署方式不同;5、耦合度不同。其中,含义不同指微服务架构是一种将一个单一应用程序开发为一组小型服务的方法ÿ…...
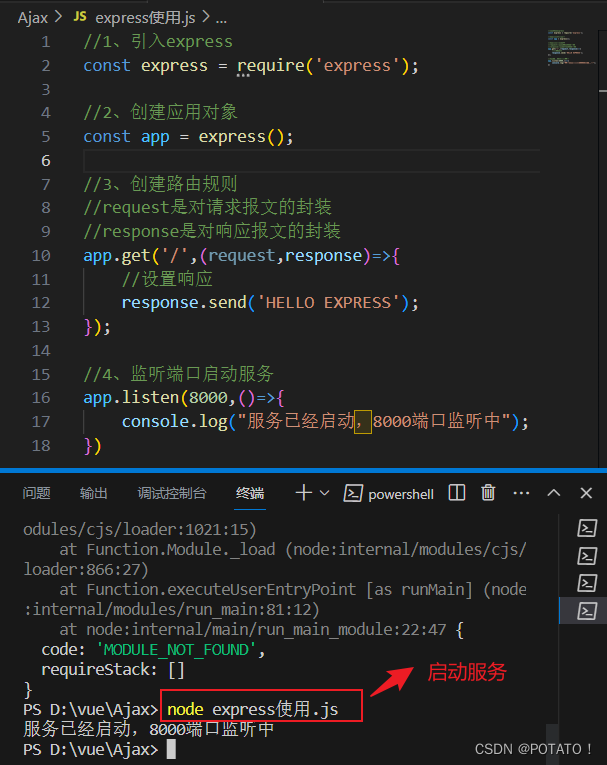
Ajax-概念、Http协议、Ajax请求及其常见问题
Ajax Ajax概念Ajax优缺点HTTP协议请求报文响应报文 Ajax案例准备工作express基本使用创建一个服务器 发送AJAX请求GET请求POST请求JSON响应 Ajax请求出现的问题IE缓存问题Ajax请求超时与网络异常处理Ajax手动取消请求Ajax重复发送请求问题 Ajax概念 AJAX 全称为Asynchronous J…...
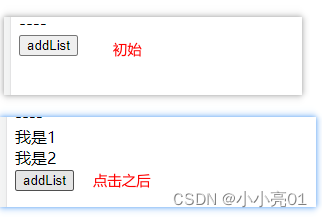
react 09之状态管理工具1 redux+ react-thunk的使用实现跨组件状态管理与异步操作
目录 react 09之状态管理工具1 redux react-thunk的使用实现跨组件状态管理与异步操作store / index.js store的入口文件index.js 在项目入口文件 引入store / actionType.js 定义action的唯一标识store / reducers / index.jsstore / actions / form.jsstore / reducers / for…...
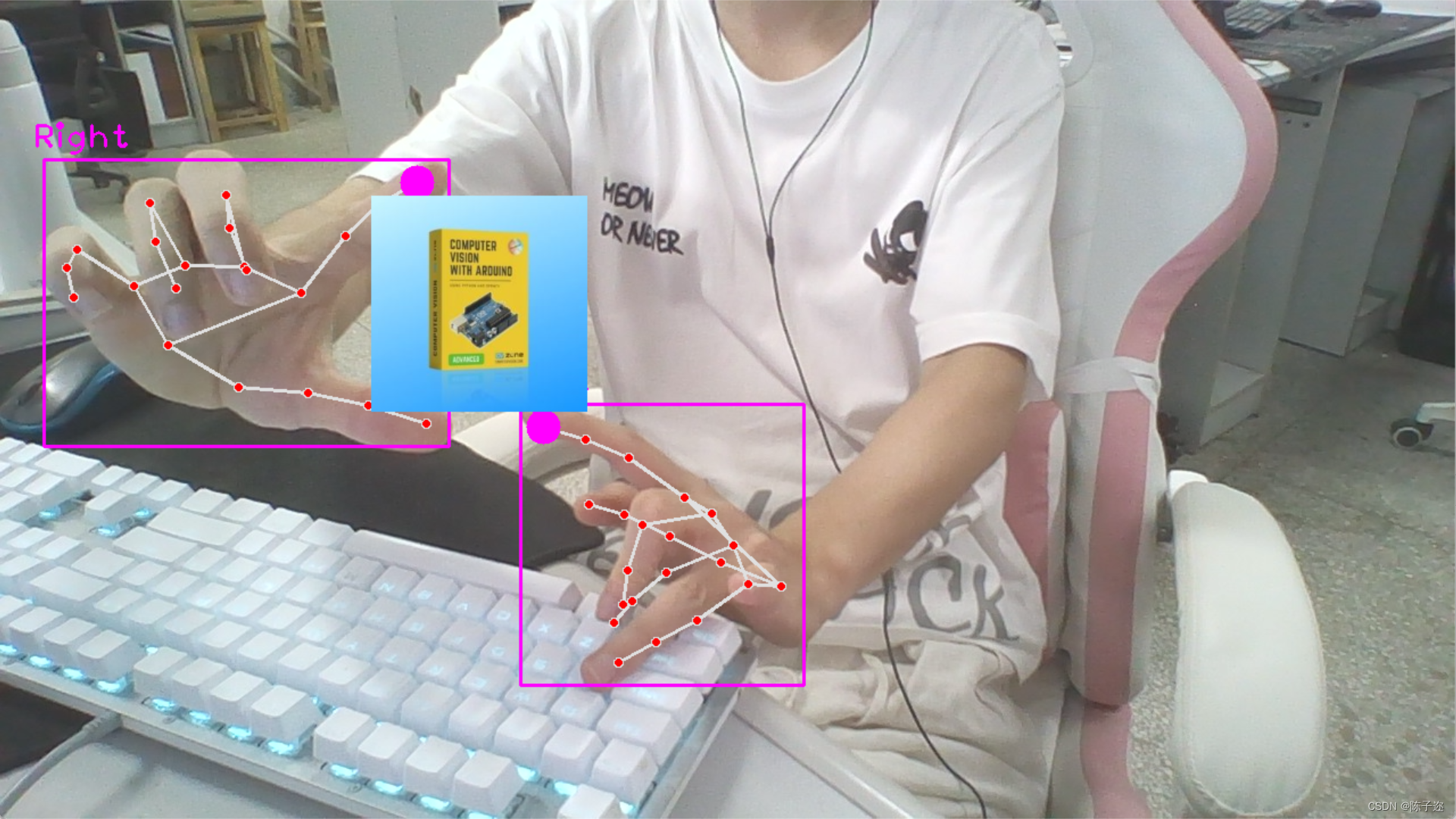
opencv实战项目 手势识别-实现尺寸缩放效果
手势识别系列文章目录 手势识别是一种人机交互技术,通过识别人的手势动作,从而实现对计算机、智能手机、智能电视等设备的操作和控制。 1. opencv实现手部追踪(定位手部关键点) 2.opencv实战项目 实现手势跟踪并返回位置信息&…...

Netty对HPACK头部压缩的支持
前言 HTTP2终于支持对头部进行压缩传输了,Netty很早就支持HTTP2了,看下Netty对HPACK的实现源码,可以对HPACK理解的更深一下。 HpackDecoder Netty内置的编解码器Http2FrameCodec专门用来对HTTP2的各种Frame进行编解码,其中就包…...

C++:替换string中的字符
1.按照位置进行替换 string的成员函数replace可以满足这种需求,其变体有很多种,请参考官方文档,以下列举常用的两种: #include <iostream> #include <string> using namespace std;int main() {string s = "hello world";s.replace(s.begin(), s.b…...

【ChatGPT】自我救赎
ChatGPT辅助学习C之【在C中如果大数据类型转小数据类型会发生什么呢?】,今天问ChatGPT一个问题,让它解析下面这个C程序: #include <iostream> #include <cstdio> using namespace std; int main() {int a;long long b532165478…...
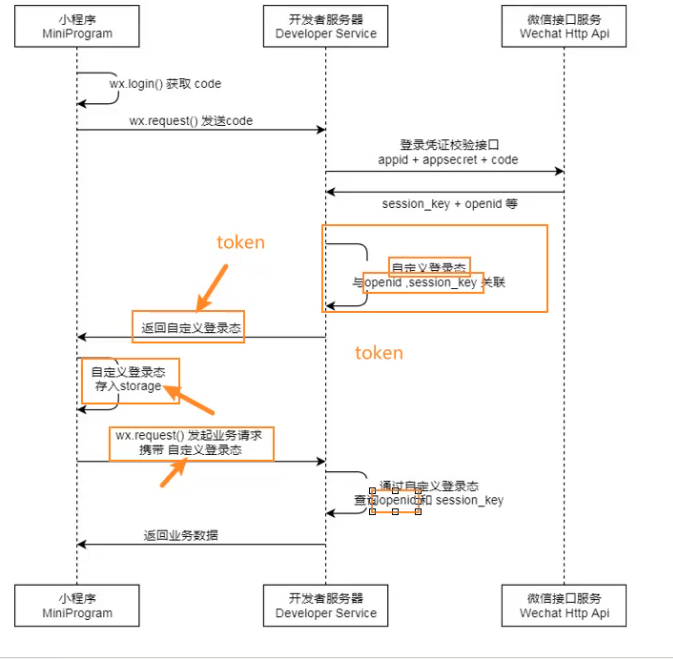
微信小程序(由浅到深)
文章目录 一. 项目基本配置1. 项目组成2. 常见的配置文件解析3. app.json全局的五大配置4.单个页面中的page配置5. App函数6.tabBar配置 二. 基本语法,事件,单位1. 语法2. 事件3. 单位 三. 数据响应式修改四 . 内置组件1. button2. image3. input4. 组件…...
冒泡排序 简单选择排序 插入排序 快速排序
bubblesort 两个for循环,从最右端开始一个一个逐渐有序 #include <stdio.h> #include <string.h> #include <stdlib.h>void bubble(int *arr, int len); int main(int argc, char *argv[]) {int arr[] {1, 2, 3, 4, 5, 6, 7};int len sizeof(…...
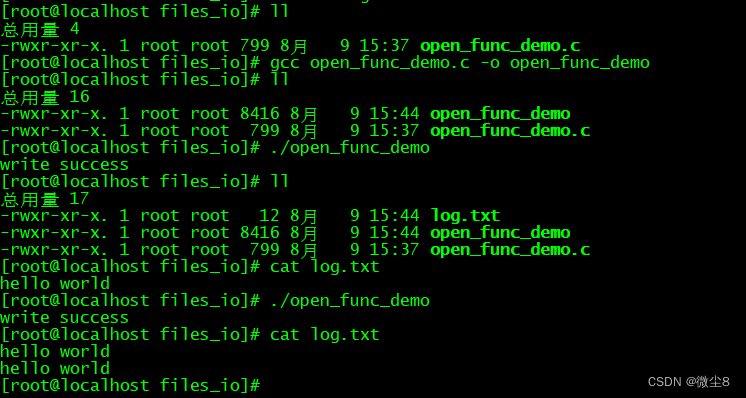
linux文件I/O之 open() 函数用法
#include <sys/types.h> #include <sys/stat.h> #include <fcntl.h> typedef unsigned int mode_t ; int open(const char *pathname, int flags); int open(const char *pathname, int flags, mode_t mode); 函数功能 打开或创建一个文件 返回值 成功…...

用Java操作MySQL数据库
新建Maven项目 创建Maven项目 添加依赖 在pom.xml的标签里加上下面的内容 如果是MySQL 5.8那么的版本号是5.x.x, 例如5.1.49 如果是MySQL 8.0那么的版本号是8.x.x, 例如 8.0.28 <dependencies><!-- https://mvnrepository.com/artifact/mysql/mysql-connector-java …...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

嵌入式学习之系统编程(九)OSI模型、TCP/IP模型、UDP协议网络相关编程(6.3)
目录 一、网络编程--OSI模型 二、网络编程--TCP/IP模型 三、网络接口 四、UDP网络相关编程及主要函数 编辑编辑 UDP的特征 socke函数 bind函数 recvfrom函数(接收函数) sendto函数(发送函数) 五、网络编程之 UDP 用…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

土建施工员考试:建筑施工技术重点知识有哪些?
《管理实务》是土建施工员考试中侧重实操应用与管理能力的科目,核心考查施工组织、质量安全、进度成本等现场管理要点。以下是结合考试大纲与高频考点整理的重点内容,附学习方向和应试技巧: 一、施工组织与进度管理 核心目标: 规…...

数据结构第5章:树和二叉树完全指南(自整理详细图文笔记)
名人说:莫道桑榆晚,为霞尚满天。——刘禹锡(刘梦得,诗豪) 原创笔记:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 上一篇:《数据结构第4章 数组和广义表》…...
