[足式机器人]Part3机构运动微分几何学分析与综合Ch03-1 空间约束曲线与约束曲面微分几何学——【读书笔记】
本文仅供学习使用
本文参考:
《机构运动微分几何学分析与综合》-王德伦、汪伟
《微分几何》吴大任
Ch01-4 平面运动微分几何学
- 3.1 空间曲线微分几何学概述
- 3.1.1 矢量表示
- 3.1.2 Frenet标架
连杆机构中的连杆与连架杆构成运动副,该运动副元素的特征点或特征线在机架坐标系中的运动轨迹曲线或曲面称为约束曲线或约束曲面,是联系刚体运动与机构运动综合的桥梁,其几何性质是机构运动综合的理论基础,既是曲线与曲面的几何学研究内容,也是连杆机构运动几何学分析与综合的课题。然而,研究曲线与曲面的几何学,微分几何学方法无疑是自然而然的选择,将其与机构运动学结合,形成以点与线的运动方式研究约束曲线与曲面几何性质,为机构运动几何学分析与综合提供理论依据。
为方便阅读后续内容,在第3.1和第3.2节简单概述微分几何学基本知识;采用微分几何量方法研究连杆机构中典型而又重要的约束曲线与约束曲面,称为空间约束曲线与约束曲面微分几何学。
3.1 空间曲线微分几何学概述
3.1.1 矢量表示
在直角坐标中表达一条空间曲线 Γ \Gamma Γ时,有:
{ x = x ( t ) y = y ( t ) z = z ( t ) \left\{ \begin{matrix} x=x(t) \\ y=y(t) \\ z=z(t) \\ \end{matrix} \right. ⎩ ⎨ ⎧x=x(t)y=y(t)z=z(t)
式中, t t t为曲线的参数,若置换自变量或者消去参数 t t t,则可写成:
{ y = y ( x ) z = z ( x ) \left\{ \begin{matrix} y=y(x) \\ z=z(x) \\ \end{matrix} \right. {y=y(x)z=z(x)
或者写成隐函数形式:
{ F 1 ( x , y , z ) = 0 F 2 ( x , y , z ) = 0 \left\{ \begin{matrix} {{F}_{1}}(x,y,z)=0 \\ {{F}_{2}}(x,y,z)=0 \\ \end{matrix} \right. {F1(x,y,z)=0F2(x,y,z)=0
若将上述 x , y , z x,y,z x,y,z置于空间固定坐标系 { O : i , j , k } \{O:i,j,k\} {O:i,j,k}中,则曲线 Γ \Gamma Γ以参数 t t t表示的矢量方程为:
Γ : R = x ( t ) i + y ( t ) j + z ( t ) k \Gamma :R=x(t)i+y(t)j+z(t)k Γ:R=x(t)i+y(t)j+z(t)k
可以将其简化为:
R = R ( t ) R=R(t) R=R(t)
式(3.4)和式(3.5)为空间曲线 Γ \Gamma Γ的矢量表达式, t t t为曲线 Γ \Gamma Γ的一般参数。在 第1章平面曲线的微分几何学 中引入了圆矢量函数用来描述曲线的矢量方程,使得形式简洁并便于计算。因此对于空间曲线 Γ \Gamma Γ的矢量方程式(3.4),可以选择任意两个坐标轴上的分量用圆矢量函数进行描述。例如,将曲线 Γ \Gamma Γ上任意点的矢径在坐标平面 O − i j O-ij O−ij上的投影矢量用圆矢量函数描述,如下图所示。
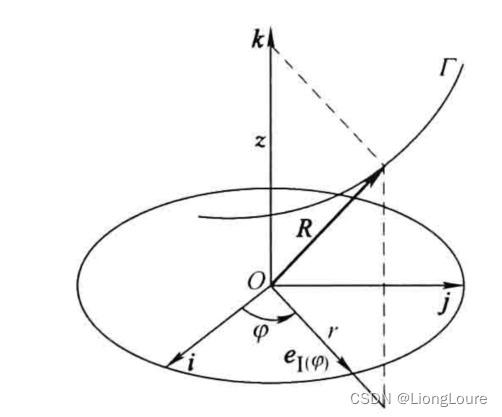
则其矢量方程可以写出另一种形式:
Γ : R = r ( φ ) e I ( φ ) + z ( φ ) k \Gamma :R=r(\varphi ){{e}_{I(\varphi )}}+z(\varphi )k Γ:R=r(φ)eI(φ)+z(φ)k
对于空间曲线 Γ \Gamma Γ,弧长参数 s s s为其自然参数,且与一般参数 t t t的关系为:
s = ∫ t a t b ∣ d R d t ∣ d t , d s = ∣ d R ∣ = ( d x d t ) 2 + ( d y d t ) 2 + ( d z d t ) 2 d t s=\int_{{{t}_{a}}}^{{{t}_{b}}}{\left| \frac{dR}{dt} \right|dt,ds=\left| dR \right|}=\sqrt{{{(\frac{dx}{dt})}^{2}}+{{(\frac{dy}{dt})}^{2}}+{{(\frac{dz}{dt})}^{2}}}dt s=∫tatb dtdR dt,ds=∣dR∣=(dtdx)2+(dtdy)2+(dtdz)2dt
空间曲线 Γ \Gamma Γ的矢量方程用弧长参数 s s s表示为: Γ : R = R ( s ) , s a ≤ s ≤ s b \Gamma :R=R(s),{{s}_{a}}\le s\le {{s}_{b}} Γ:R=R(s),sa≤s≤sb
注:书中为 Γ : R = R ( s ) , s a ≤ a ≤ s b \Gamma :R=R(s),{{s}_{a}}\le a\le {{s}_{b}} Γ:R=R(s),sa≤a≤sb
【例3-1】 球面曲线如下图所示:
对于球面曲线 Γ \Gamma Γ,习惯于将直角坐标系 { O : i , j , k } \{O:i,j,k\} {O:i,j,k}原点置于球心,则用直角坐标表示为:
{ x = x ( t ) , y = y ( t ) , z = z ( t ) x 2 + y 2 + z 2 = R 2 \left\{ \begin{matrix} x=x(t),y=y(t),z=z(t) \\ {{x}^{2}}+{{y}^{2}}+{{z}^{2}}={{R}^{2}} \\ \end{matrix} \right. {x=x(t),y=y(t),z=z(t)x2+y2+z2=R2
式中, R R R为球面半径, t t t为球面曲线的参数,若置换自变量或者消去参数 t t t,可写成:
{ z = z ( x , y ) x 2 + y 2 + z 2 = R 2 \left\{ \begin{matrix} z=z(x,y) \\ {{x}^{2}}+{{y}^{2}}+{{z}^{2}}={{R}^{2}} \\ \end{matrix} \right. {z=z(x,y)x2+y2+z2=R2
由于球面曲线上的点始终分布在一球面上,因此往往用球面坐标表示曲线为:
δ = δ ( t ) , φ = φ ( t ) , r = R \delta =\delta (t),\varphi =\varphi (t),r=R δ=δ(t),φ=φ(t),r=R
式中, δ \delta δ是由原点0到曲线上点 P P P的有向线段 O P OP OP与 k k k的夹角; φ \varphi φ是 O P OP OP在 O − i j O-ij O−ij面上的投影与i的夹角, δ \delta δ和 φ \varphi φ的取值范围分别为 [ 0 , π ] [0,\pi ] [0,π]和 [ 0 , 2 π ] [0,2\pi ] [0,2π]。点 P P P在坐标系 { O : i , j , k } \{O:i,j,k\} {O:i,j,k}中的球面坐标与直角坐标之间具有如下转换关系:
x = R sin δ cos φ , y = R sin δ sin φ , z = R cos δ x=R\sin \delta \cos \varphi ,y=R\sin \delta \sin \varphi ,z=R\cos \delta x=Rsinδcosφ,y=Rsinδsinφ,z=Rcosδ
将上述 x , y , z x,y,z x,y,z置于坐标系 { O : i , j , k } \{O:i,j,k\} {O:i,j,k}中,则球面曲线以参数 t t t表示的矢量方程为:
Γ : R = R ( t ) = x ( t ) i + y ( t ) j + z ( t ) k \Gamma :R=R(t)=x(t)i+y(t)j+z(t)k Γ:R=R(t)=x(t)i+y(t)j+z(t)k
若通过圆矢量函数表示球面曲线的矢量方程,则为:
R = R sin δ ( φ ) e I ( φ ) + R cos δ ( φ ) k R=R\sin \delta (\varphi ){{e}_{I(\varphi )}}+R\cos \delta (\varphi )k R=Rsinδ(φ)eI(φ)+Rcosδ(φ)k
比较式(E3-1.1)、式(E3-1.4)与式(E3-1.6)可知,采用矢量表示的球面曲线比其他方式表达要简单的多。
【例3-2】 圆柱面曲线如下图所示:
圆柱面曲线在直角坐标系 { O : i , j , k } \{O:i,j,k\} {O:i,j,k}中的方程为:
{ x = r 0 cos φ y = r 0 sin φ z = z ( φ ) \left\{ \begin{matrix} x={{r}_{0}}\cos \varphi \\ y={{r}_{0}}\sin \varphi \\ z=z(\varphi ) \\ \end{matrix} \right. ⎩ ⎨ ⎧x=r0cosφy=r0sinφz=z(φ)
式中, r 0 {{r}_{0}} r0为圆柱面半径。若通过圆矢量函数表示圆柱面曲线的矢量方程,则为:
R = r 0 e I ( φ ) + z ( φ ) k R={{r}_{0}}{{e}_{I(\varphi )}}+z(\varphi )k R=r0eI(φ)+z(φ)k
3.1.2 Frenet标架
空间曲线 Γ ⃗ : R ⃗ = R ⃗ ( s ) \vec{\varGamma}:\vec{R}=\vec{R}\left( s \right) Γ:R=R(s) 在任意点 P P P处有两个无限接近位置的点连线组成切线,其单位切矢 α ⃗ ( s ) = d R ⃗ ( s ) d s \vec{\alpha}\left( s \right) =\frac{\mathrm{d}\vec{R}\left( s \right)}{\mathrm{d}s} α(s)=dsdR(s)始终指向曲线弧长增加的方向,将切矢 α ⃗ ( s ) \vec{\alpha}\left( s \right) α(s) 对弧长参数求导,可得:
d α ⃗ ( s ) d s = k ( s ) β ⃗ ( s ) \frac{\mathrm{d}\vec{\alpha}\left( s \right)}{\mathrm{d}s}=k\left( s \right) \vec{\beta}\left( s \right) dsdα(s)=k(s)β(s)
其中, k ( s ) k\left( s \right) k(s) 称为曲线 Γ ⃗ \vec{\varGamma} Γ 在点 P P P 处的曲率,即三个无限接近位置点构成空间曲线在该点处的密切平面,曲率是空间曲线在密切平面内的弯曲程度,体现了曲线的切矢的倾斜角对弧长参数的变化率。与平面曲线曲率不同,空间曲线的曲率非负。 β ⃗ ( s ) \vec{\beta}\left( s \right) β(s) 称为曲线 Γ ⃗ \vec{\varGamma} Γ 在点 P P P 处的主法矢,指向了曲线在该点的曲率中心。当 k ( s ) ≠ 0 k\left( s \right) \ne 0 k(s)=0 时,其倒数 ρ ( s ) = 1 / k ( s ) \rho \left( s \right) =1/k\left( s \right) ρ(s)=1/k(s) 称为曲线 Γ ⃗ \vec{\varGamma} Γ 的曲率半径,则曲线 Γ ⃗ \vec{\varGamma} Γ 曲率中心 C C C的矢量为:
R ⃗ C = R ⃗ P + ρ ⋅ β ⃗ \vec{R}_{\mathrm{C}}=\vec{R}_{\mathrm{P}}+\rho \cdot \vec{\beta} RC=RP+ρ⋅β
由空间曲线 Γ ⃗ \vec{\varGamma} Γ 在点 P P P 处的切矢 α ⃗ ( s ) \vec{\alpha}\left( s \right) α(s) 和主法矢 β ⃗ ( s ) \vec{\beta}\left( s \right) β(s) 可以构建矢量 γ ⃗ ( s ) = α ⃗ ( s ) × β ⃗ ( s ) \vec{\gamma}\left( s \right) =\vec{\alpha}\left( s \right) \times \vec{\beta}\left( s \right) γ(s)=α(s)×β(s) ,称之为曲线的副法矢,从而在空间曲线 Γ ⃗ \vec{\varGamma} Γ 上构造了单位右手系正交标架 { R ⃗ ( s ) ; α ⃗ ( s ) , β ⃗ ( s ) , γ ⃗ ( s ) } \left\{ \vec{R}\left( s \right) ;\vec{\alpha}\left( s \right) ,\vec{\beta}\left( s \right) ,\vec{\gamma}\left( s \right) \right\} {R(s);α(s),β(s),γ(s)} ,称为曲线 Γ ⃗ \vec{\varGamma} Γ 在点 P P P 的Frenet标架。
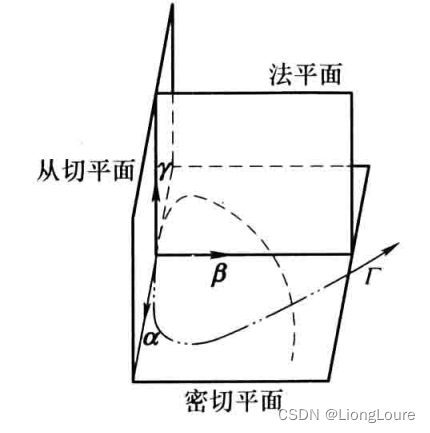
对于空间曲线 Γ ⃗ \vec{\varGamma} Γ 在 P P P 点的Frenet标架 { R ⃗ ( s ) ; α ⃗ ( s ) , β ⃗ ( s ) , γ ⃗ ( s ) } \left\{ \vec{R}\left( s \right) ;\vec{\alpha}\left( s \right) ,\vec{\beta}\left( s \right) ,\vec{\gamma}\left( s \right) \right\} {R(s);α(s),β(s),γ(s)} ,其中标矢 α ⃗ ( s ) \vec{\alpha}\left( s \right) α(s) 和 β ⃗ ( s ) \vec{\beta}\left( s \right) β(s) 确定了密切平面, β ⃗ ( s ) \vec{\beta}\left( s \right) β(s) 和 γ ⃗ ( s ) \vec{\gamma}\left( s \right) γ(s) 确定的平面称为法平面,而 α ⃗ ( s ) \vec{\alpha}\left( s \right) α(s) 和 γ ⃗ ( s ) \vec{\gamma}\left( s \right) γ(s) 确定的平面称为从切平面。可见Frenet标架由三个同空间曲线紧密联系的向量所组成,其微分运算公式为:
{ d R ⃗ ( s ) d s = α ⃗ ( s ) d α ⃗ ( s ) d s = k ( s ) β ⃗ ( s ) d β ⃗ ( s ) d s = − k ( s ) α ⃗ ( s ) + τ ( s ) γ ⃗ ( s ) d γ ⃗ ( s ) d s = − τ ( s ) β ⃗ ( s ) \begin{cases} \begin{array}{c} \frac{\mathrm{d}\vec{R}\left( s \right)}{\mathrm{d}s}=\vec{\alpha}\left( s \right)\\ \frac{\mathrm{d}\vec{\alpha}\left( s \right)}{\mathrm{d}s}=k\left( s \right) \vec{\beta}\left( s \right)\\ \end{array}\\ \begin{array}{c} \frac{\mathrm{d}\vec{\beta}\left( s \right)}{\mathrm{d}s}=-k\left( s \right) \vec{\alpha}\left( s \right) +\tau \left( s \right) \vec{\gamma}\left( s \right)\\ \frac{\mathrm{d}\vec{\gamma}\left( s \right)}{\mathrm{d}s}=-\tau \left( s \right) \vec{\beta}\left( s \right)\\ \end{array}\\ \end{cases} ⎩ ⎨ ⎧dsdR(s)=α(s)dsdα(s)=k(s)β(s)dsdβ(s)=−k(s)α(s)+τ(s)γ(s)dsdγ(s)=−τ(s)β(s)
其中, τ ( s ) \tau \left( s \right) τ(s) 称为空间曲线 Γ ⃗ \vec{\varGamma} Γ 在点 P P P 处的挠率,它衡量了曲线在点 $P$ 的(密切平面)副法矢 $\vec{\gamma}\left( s \right)$ 倾斜角对弧长的变化率,从而描述了曲线在该点偏离密切平面的程度。上式也称为空间曲线的Frenet公式。
由Frenet公式可以得到空间曲线 Γ ⃗ \vec{\varGamma} Γ 曲率 k k k 和挠率 τ \tau τ 的表达式为:
k = ∣ d 2 R ⃗ ( s ) d s 2 ∣ , τ = ( d R ⃗ ( s ) d s , d 2 R ⃗ ( s ) d s 2 , d 3 R ⃗ ( s ) d s 3 ) / ∣ d 2 R ⃗ ( s ) d s 2 ∣ 2 k=\left| \frac{\mathrm{d}^2\vec{R}\left( s \right)}{\mathrm{d}s^2} \right|,\tau =\left( \frac{\mathrm{d}\vec{R}\left( s \right)}{\mathrm{d}s},\frac{\mathrm{d}^2\vec{R}\left( s \right)}{\mathrm{d}s^2},\frac{\mathrm{d}^3\vec{R}\left( s \right)}{\mathrm{d}s^3} \right) /\left| \frac{\mathrm{d}^2\vec{R}\left( s \right)}{\mathrm{d}s^2} \right|^2 k= ds2d2R(s) ,τ=(dsdR(s),ds2d2R(s),ds3d3R(s))/ ds2d2R(s) 2
若空间曲线 Γ ⃗ \vec{\varGamma} Γ 是以一般参数 t t t 进行描述的,则其曲率 k ( s ) k(s) k(s) 和挠率 τ ( s ) \tau \left( s \right) τ(s) 的表达式为:
k = ∣ d R ⃗ d t × d 2 R ⃗ d t 2 ∣ / ∣ d R ⃗ d t ∣ 3 , τ = ( d R ⃗ d t , d 2 R ⃗ d t 2 , d 3 R ⃗ d t 3 ) / ( d R ⃗ d t × d 2 R ⃗ d t 2 ) 2 k=\left| \frac{\mathrm{d}\vec{R}}{\mathrm{d}t}\times \frac{\mathrm{d}^2\vec{R}}{\mathrm{d}t^2} \right|/\left| \frac{\mathrm{d}\vec{R}}{\mathrm{d}t} \right|^3,\tau =\left( \frac{\mathrm{d}\vec{R}}{\mathrm{d}t},\frac{\mathrm{d}^2\vec{R}}{\mathrm{d}t^2},\frac{\mathrm{d}^3\vec{R}}{\mathrm{d}t^3} \right) /\left( \frac{\mathrm{d}\vec{R}}{\mathrm{d}t}\times \frac{\mathrm{d}^2\vec{R}}{\mathrm{d}t^2} \right) ^2 k= dtdR×dt2d2R / dtdR 3,τ=(dtdR,dt2d2R,dt3d3R)/(dtdR×dt2d2R)2
对于空间曲线来说,曲率 k ( s ) k(s) k(s) 和挠率 τ ( s ) \tau \left( s \right) τ(s) 不依赖于坐标系的选定。是空间曲线的不变量,能够唯一地确定空间曲线,可以将 k = k ( s ) , τ = τ ( s ) k=k\left( s \right) ,\tau =\tau \left( s \right) k=k(s),τ=τ(s) 称为空间曲线的自然方程。于是有:
定理3.1:在区间 0 ⩽ s ⩽ l 0\leqslant s\leqslant l 0⩽s⩽l上任意给定连续可微函数 $k\left( s \right) >0 $ 和连续函数 τ ( s ) \tau \left( s \right) τ(s) 以及初始右手系正交标架 { R ⃗ 0 ; α ⃗ 0 , β ⃗ 0 , γ ⃗ 0 } \left\{ \vec{R}_0;\vec{\alpha}_0,\vec{\beta}_0,\vec{\gamma}_0 \right\} {R0;α0,β0,γ0} ,则一定有且仅有一条以 s s s 为弧长、以 k ( s ) k\left( s \right) k(s) 为曲率、 τ ( s ) \tau \left( s \right) τ(s) 为挠率的空间有向曲线。
建立了空间曲线 Γ ⃗ \vec{\varGamma} Γ 上 P P P 点处的Frenet标架 { R ⃗ ( s ) ; α ⃗ ( s ) , β ⃗ ( s ) , γ ⃗ ( s ) } \left\{ \vec{R}\left( s \right) ;\vec{\alpha}\left( s \right) ,\vec{\beta}\left( s \right) ,\vec{\gamma}\left( s \right) \right\} {R(s);α(s),β(s),γ(s)} ,可将曲线 Γ ⃗ \vec{\varGamma} Γ 在点 P P P的邻域内按照泰勒公式展开。假定曲线 Γ ⃗ \vec{\varGamma} Γ 在点 P P P 处的弧长为 s s s,则有:
R ⃗ ( s + Δ s ) = R ⃗ ( s ) + d R ⃗ ( s ) d s Δ s + 1 2 ! d 2 R ⃗ ( s ) d s 2 ( Δ s ) 2 + ⋯ + 1 n ! d n R ⃗ ( s ) d s n ( Δ s ) n + ε n ( s , Δ s ) ( Δ s ) n \vec{R}\left( s+\varDelta s \right) =\vec{R}\left( s \right) +\frac{\mathrm{d}\vec{R}\left( s \right)}{\mathrm{d}s}\varDelta s+\frac{1}{2!}\frac{\mathrm{d}^2\vec{R}\left( s \right)}{\mathrm{d}s^2}\left( \varDelta s \right) ^2+\cdots +\frac{1}{n!}\frac{\mathrm{d}^n\vec{R}\left( s \right)}{\mathrm{d}s^n}\left( \varDelta s \right) ^n+\varepsilon _{\mathrm{n}}\left( s,\varDelta s \right) \left( \varDelta s \right) ^n R(s+Δs)=R(s)+dsdR(s)Δs+2!1ds2d2R(s)(Δs)2+⋯+n!1dsndnR(s)(Δs)n+εn(s,Δs)(Δs)n
式中, lim Δ s → 0 ε n ( s , Δ s ) = 0 , d R ⃗ d s = α ⃗ , d 2 R ⃗ d s 2 = k β ⃗ , d 3 R ⃗ d s 3 = − k 2 α ⃗ + d k d s β ⃗ + k τ γ ⃗ \lim_{\varDelta s\rightarrow 0} \varepsilon _{\mathrm{n}}\left( s,\varDelta s \right) =0,\frac{\mathrm{d}\vec{R}}{\mathrm{d}s}=\vec{\alpha},\frac{\mathrm{d}^2\vec{R}}{\mathrm{d}s^2}=k\vec{\beta},\frac{\mathrm{d}^3\vec{R}}{\mathrm{d}s^3}=-k^2\vec{\alpha}+\frac{\mathrm{d}k}{\mathrm{d}s}\vec{\beta}+k\tau \vec{\gamma} limΔs→0εn(s,Δs)=0,dsdR=α,ds2d2R=kβ,ds3d3R=−k2α+dsdkβ+kτγ ,并以此可以得到矢径 R ⃗ ( s ) \vec{R}\left( s \right) R(s) 关于弧长参数的各阶导数。
相关文章:

[足式机器人]Part3机构运动微分几何学分析与综合Ch03-1 空间约束曲线与约束曲面微分几何学——【读书笔记】
本文仅供学习使用 本文参考: 《机构运动微分几何学分析与综合》-王德伦、汪伟 《微分几何》吴大任 Ch01-4 平面运动微分几何学 3.1 空间曲线微分几何学概述3.1.1 矢量表示3.1.2 Frenet标架 连杆机构中的连杆与连架杆构成运动副,该运动副元素的特征点或特…...

pytest框架快速进阶篇-pytest前置和pytest后置,skipif跳过用例
一、Pytest的前置和后置方法 1.Pytest可以集成unittest实现前置和后置 importunittestimportpytestclassTestCase(unittest.TestCase):defsetUp(self)->None:print(unittest每个用例前置)deftearDown(self)->None:print(unittest每个用例后置)classmethoddefsetUpClass…...

Python 基础语法 | 常量表达式,变量,注释,输入输出
常量和表达式 我们可以把 Python 当成一个计算器,来进行一些算术运算 print(1 2 - 3) # 0 print(1 2 * 3) # 7 print(1 2 / 3) # 1.6666666666666665注意: print 是一个 Python 内置的 函数可以使用 - * / () 等运算符进行算术运算,先…...

SQL | 分组数据
10-分组数据 两个新的select子句:group by子句和having子句。 10.1-数据分组 上面我们学到了,使用SQL中的聚集函数可以汇总数据,这样,我们就能够对行进行计数,计算和,计算平均数。 目前为止,…...
)
软件测试技术之如何编写测试用例(6)
四、客户端兼容性测试 1、平台测试 市场上有很多不同的操作系统类型,最常见的有Windows、Unix、Macintosh、Linux等。Web应用系统的最终用户究竟使用哪一种操作系统,取决于用户系统的配置。这样,就可能会发生兼容性问题,同一个应…...

论文阅读——Adversarial Eigen Attack on Black-Box Models
Adversarial Eigen Attack on Black-Box Models 作者:Linjun Zhou, Linjun Zhou 攻击类别:黑盒(基于梯度信息),白盒模型的预训练模型可获得,但训练数据和微调预训练模型的数据不可得ÿ…...
-[自定义对话记忆与自定义记忆类])
自然语言处理从入门到应用——LangChain:记忆(Memory)-[自定义对话记忆与自定义记忆类]
分类目录:《自然语言处理从入门到应用》总目录 自定义对话记忆 本节介绍了几种自定义对话记忆的方法: from langchain.llms import OpenAI from langchain.chains import ConversationChain from langchain.memory import ConversationBufferMemoryllm…...

【C/C++】STL queue 非线程安全接口,危险!
STL 中的 queue 是非线程安全的,一个组合操作:front(); pop() 先读取队首元素然后删除队首元素,若是有多个线程执行这个组合操作的话,可能会发生执行序列交替执行,导致一些意想不到的行为。因此需要重新设计线程安全的…...
执行Lua脚本后一直查询不到Redis中的数据(附带问题详细排查过程,一波三折)
文章目录 执行Lua脚本后一直查询不到Redis中的数据(附带详细问题排查过程,一波三折)问题背景问题1:Lua脚本无法切库问题2:RedisTemlate切库报错问题3:序列化导致数据不一致问题4:Lua脚本中单引号…...
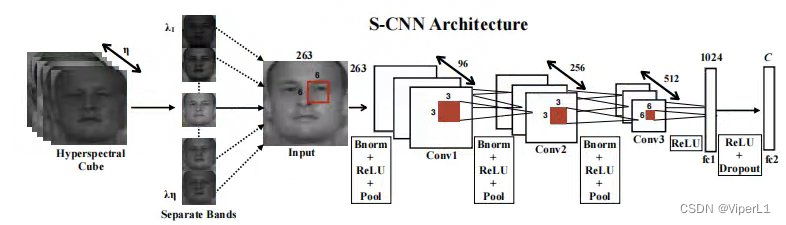
[高光谱]PyTorch使用CNN对高光谱图像进行分类
项目原地址: Hyperspectral-Classificationhttps://github.com/eecn/Hyperspectral-ClassificationDataLoader讲解: [高光谱]使用PyTorch的dataloader加载高光谱数据https://blog.csdn.net/weixin_37878740/article/details/130929358 一、模型加载 在…...
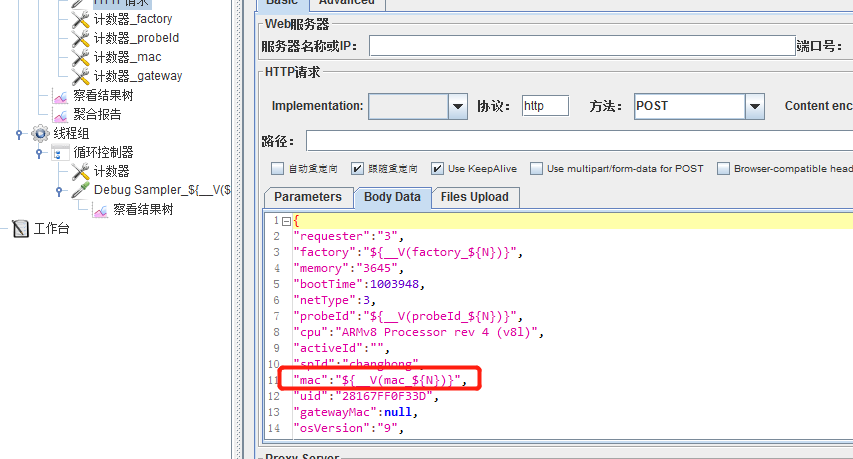
jmeter获取mysql数据
JDBC Connection Configuration Database URL: jdbc:mysql:// 数据库地址 /库名 JDBC Driver class:com.mysql.jdbc.Driver Username:账号 Password:密码 JDBC Request 字段含义 字段含义 Variable Name Bound to Pool 数据库连接池配置…...
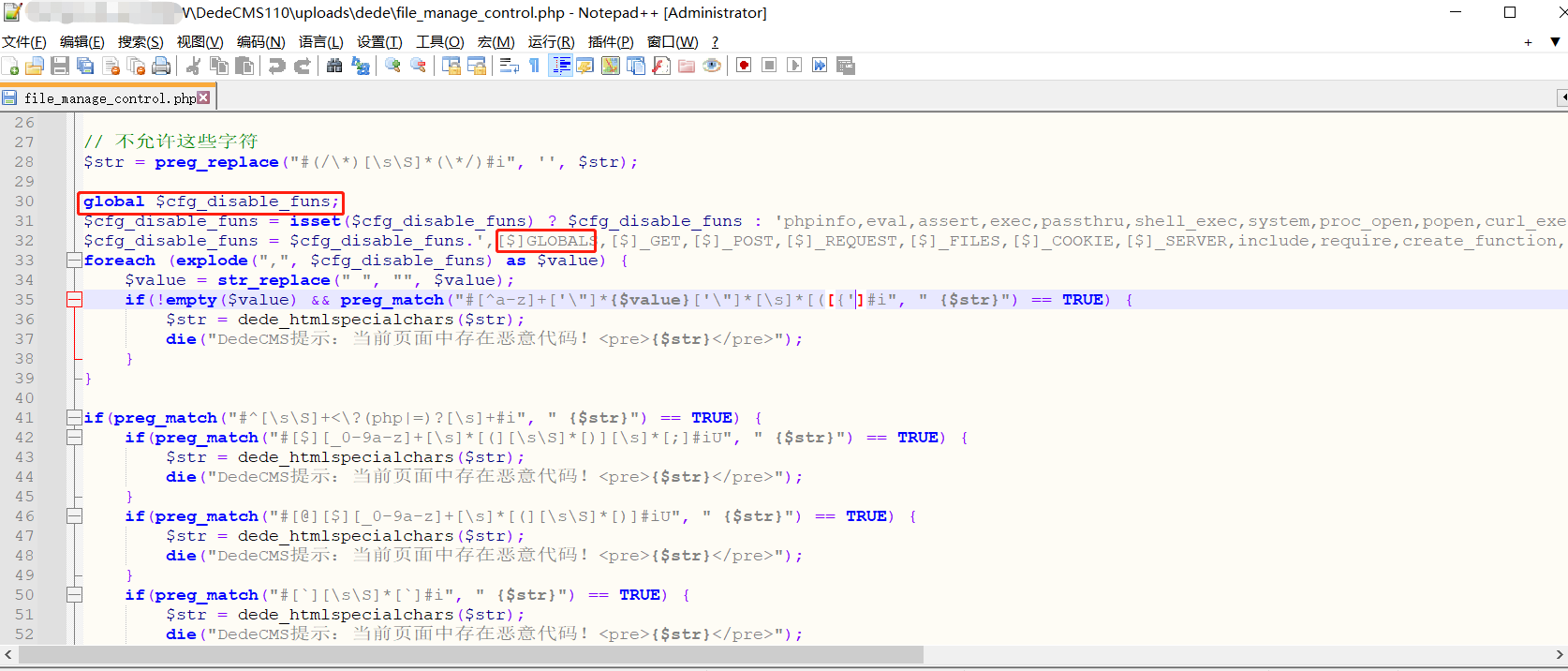
Dedecms V110最新版RCE---Tricks
前言 刚发现Dedecms更新了发布版本,顺便测试一下之前的day有没有修复,突然想到了新的tricks去实现RCE。 文章发布的时候估计比较晚了,一直没时间写了。 利用 /uploads/dede/article_string_mix.php /uploads/dede/article_template_rand.…...
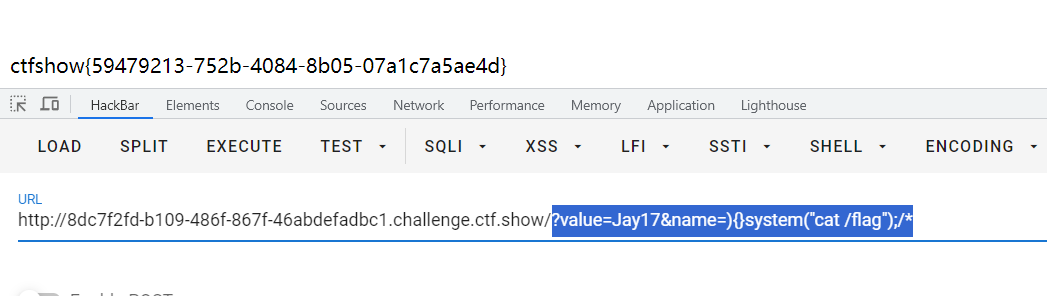
CTFshow 限时活动 红包挑战7、红包挑战8
CTFshow红包挑战7 写不出来一点,还是等了官方wp之后才复现。 直接给了源码 <?php highlight_file(__FILE__); error_reporting(2);extract($_GET); ini_set($name,$value);system("ls ".filter($_GET[1])."" );function filter($cmd){$cmd…...

Redis使用Lua脚本和Redisson来保证库存扣减中的原子性和一致性
文章目录 前言1.使用SpringBoot Redis 原生实现方式2.使用redisson方式实现3. 使用RedisLua脚本实现3.1 lua脚本代码逻辑 3.2 与SpringBoot集成 4. Lua脚本方式和Redisson的方式对比5. 源码地址6. Redis从入门到精通系列文章7. 参考文档 前言 背景:最近有社群技术交…...
【从零开始学Kaggle竞赛】泰坦尼克之灾
目录 0.准备1.问题分析挑战流程数据集介绍结果提交 2.代码实现2.1 加载数据2.1.1 加载训练数据2.1.2 加载测试数据 2.2 数据分析2.3 模型建立与预测 3.结果提交 0.准备 注册kaggle账号后,进入titanic竞赛界面 https://www.kaggle.com/competitions/titanic 进入后界…...

输出无重复的3位数和计算无人机飞行坐标
编程题总结 题目一:输出无重复的3位数 题目描述 从{1,2,3,4,5,6,7,8,9}中随机挑选不重复的5个数字作为输入数组‘selectedDigits’,能组成多少个互不相同且无重复数字的3位数?请编写程》序,从小到大顺序,以数组形式输出这些3位…...

muduo 29 异步日志
目录 Muduo双缓冲异步日志模型: 异步日志实现: 为什么要实现非阻塞的日志...

Qt 对象序列化/反序列化
阅读本文大概需要 3 分钟 背景 日常开发过程中,避免不了对象序列化和反序列化,如果你使用 Qt 进行开发,那么有一种方法实现起来非常简单和容易。 实现 我们知道 Qt 的元对象系统非常强大,基于此属性我们可以实现对象的序列化和…...
)
从零学算法(非官方题库)
输入两棵二叉树A和B,判断B是不是A的子结构。(约定空树不是任意一个树的子结构) B是A的子结构, 即 A中有出现和B相同的结构和节点值。 例如: 给定的树 A:3/ \4 5/ \1 2给定的树 B:4 / 1返回 true,因为 B 与 A 的一个子树拥有相…...

Java # JVM内存管理
一、运行时数据区域 程序计数器、Java虚拟机栈、本地方法栈、Java堆、方法区、运行时常量池、直接内存 二、HotSpot虚拟机对象 对象创建: 引用检查类加载检查分配内存空间:指针碰撞、空闲列表分配空间初始化对象信息设置(对象头内࿰…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...