matlab使用教程(15)—图论基础
1.有向图和无向图
1.1什么是图?
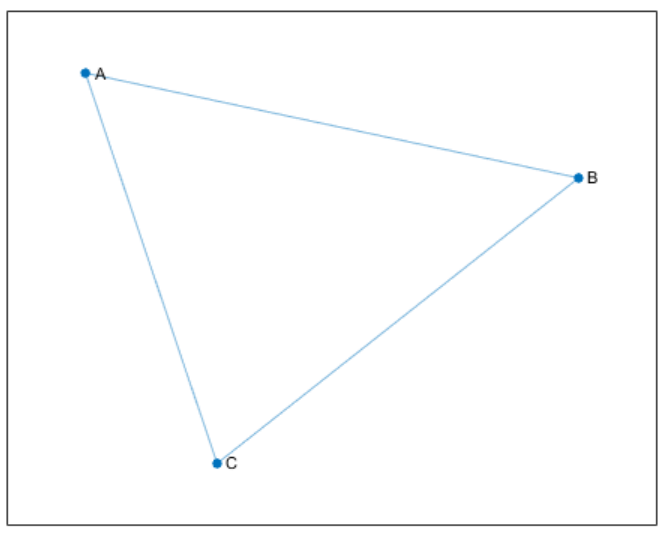
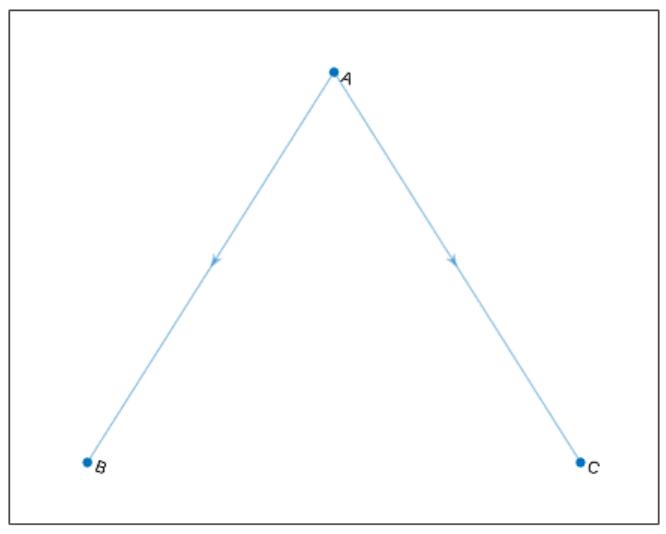
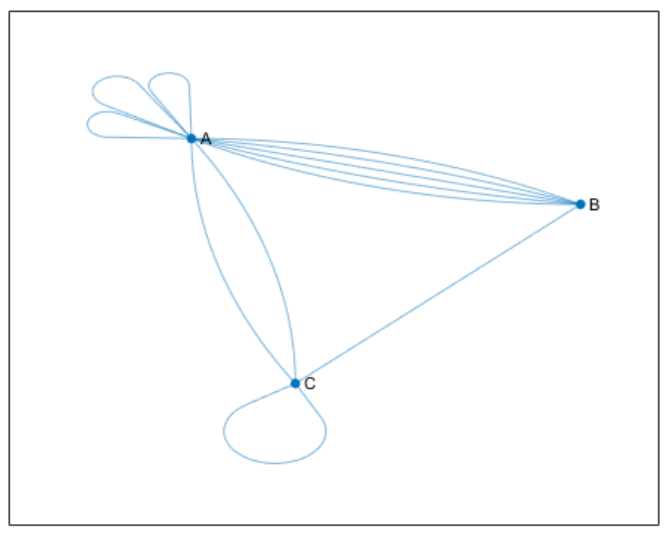
1.2 自环和多重图
2.创建图
2.1 邻接矩阵
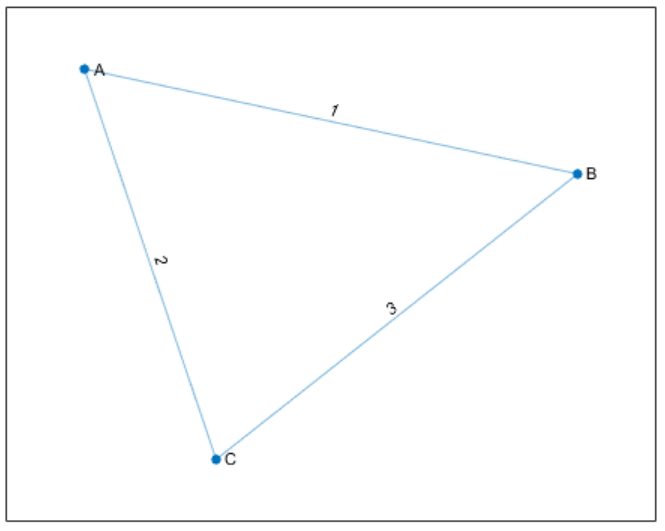
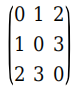
2.2 边列表

3.图节点 ID
4.修改或查询现有图
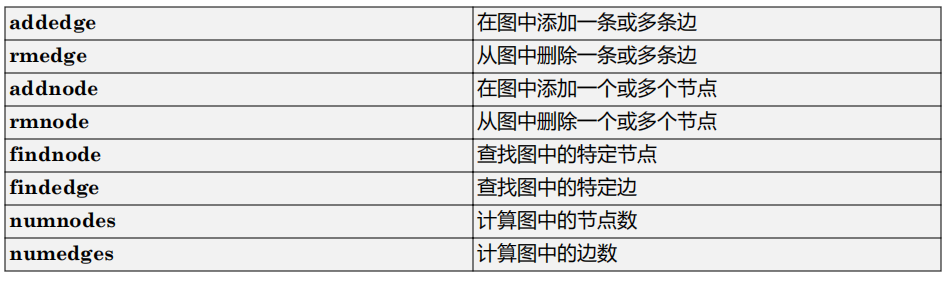

相关文章:

matlab使用教程(15)—图论基础
1.有向图和无向图 1.1什么是图? 图是表示各种关系的节点和边的集合: • 节点 是与对象对应的顶点。 • 边 是对象之间的连接。 • 图的边有时会有权重 ,表示节点之间的每个连接的强度(或一些其他属性)。 这些定…...
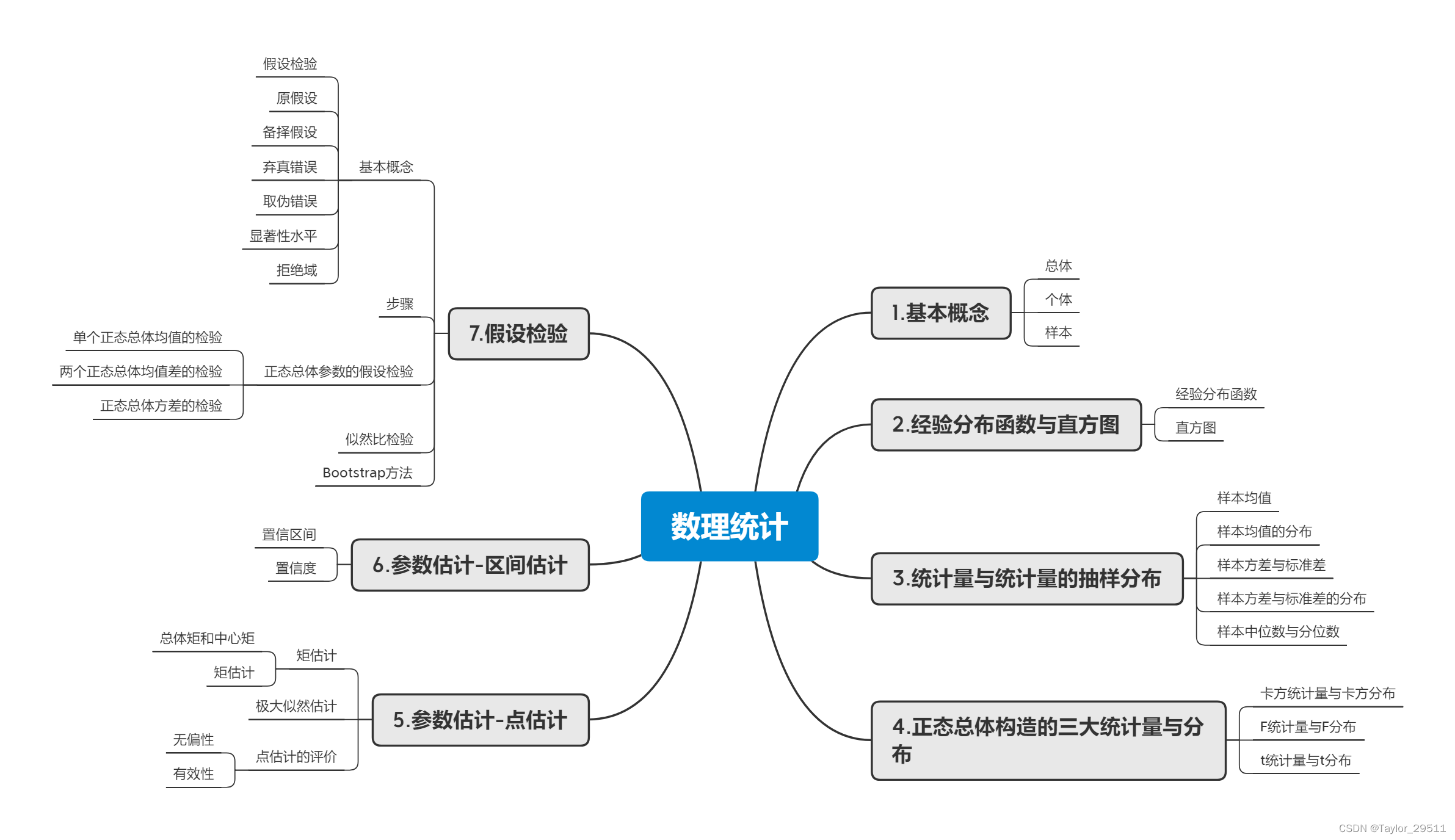
【量化课程】02_4.数理统计的基本概念
2.4_数理统计的基本概念 数理统计思维导图 更多详细内容见notebook 1.基本概念 总体:研究对象的全体,它是一个随机变量,用 X X X表示。 个体:组成总体的每个基本元素。 简单随机样本:来自总体 X X X的 n n n个相互…...

【计算机视觉|生成对抗】改进的生成对抗网络(GANs)训练技术
本系列博文为深度学习/计算机视觉论文笔记,转载请注明出处 标题:Improved Techniques for Training GANs 链接:[1606.03498v1] Improved Techniques for Training GANs (arxiv.org) 摘要 本文介绍了一系列应用于生成对抗网络(G…...
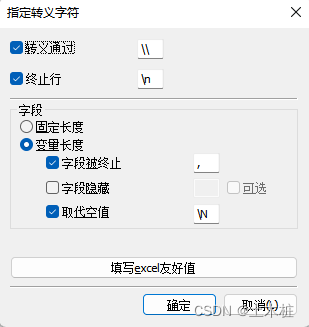
SQLyog中导入CSV文件入库到MySQL中
1.在数据库中新建一个表,设置列名(与待导入文件一致),字段可以多出几个都可以 2.右键表名,导入- - >导入使用本地加载的CSV数据 选择使用加载本地CVS数据 3.指定好转义字符,将终止设置为,号(英文状态下…...

Spring Security6 最新版配置该怎么写,该如何实现动态权限管理
Spring Security 在最近几个版本中配置的写法都有一些变化,很多常见的方法都废弃了,并且将在未来的 Spring Security7 中移除,因此又补充了一些新的内容,重新发一下,供各位使用 Spring Security 的小伙伴们参考。 接下…...

CommandLineRunner 和 ApplicationRunner 用于Spring Boot 应用启动后执行特定逻辑
CommandLineRunner 和 ApplicationRunner 都是 Spring Boot 中用于在应用启动后执行特定逻辑的接口。它们的主要区别在于传递的参数类型和执行顺序。下面我将为您详细解释它们的用途、使用案例以及执行顺序。 CommandLineRunner CommandLineRunner 是一个接口,它有…...
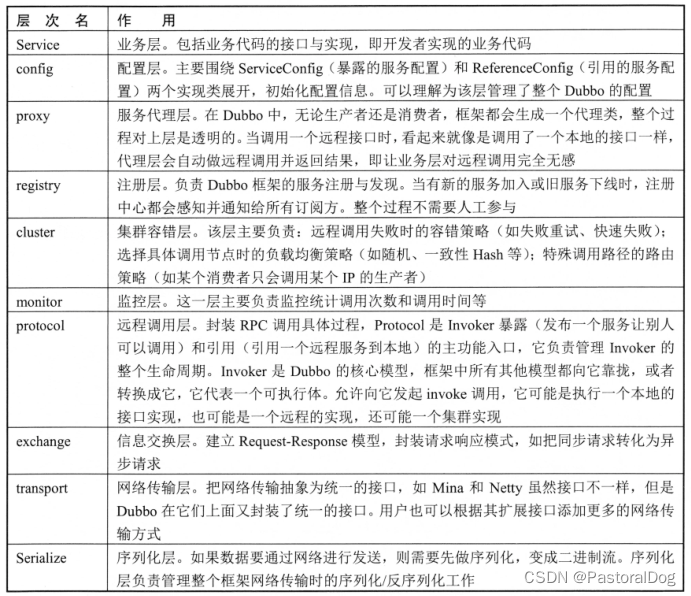
一、Dubbo 简介与架构
一、Dubbo 简介与架构 1.1 应用架构演进过程 单体应用:JEE、MVC分布式应用:SOA、微服务化 1.2 Dubbo 简介一种分布式 RPC 框架,对专业知识(序列化/反序列化、网络、多线程、设计模式、性能优化等)进行了更高层的抽象和…...
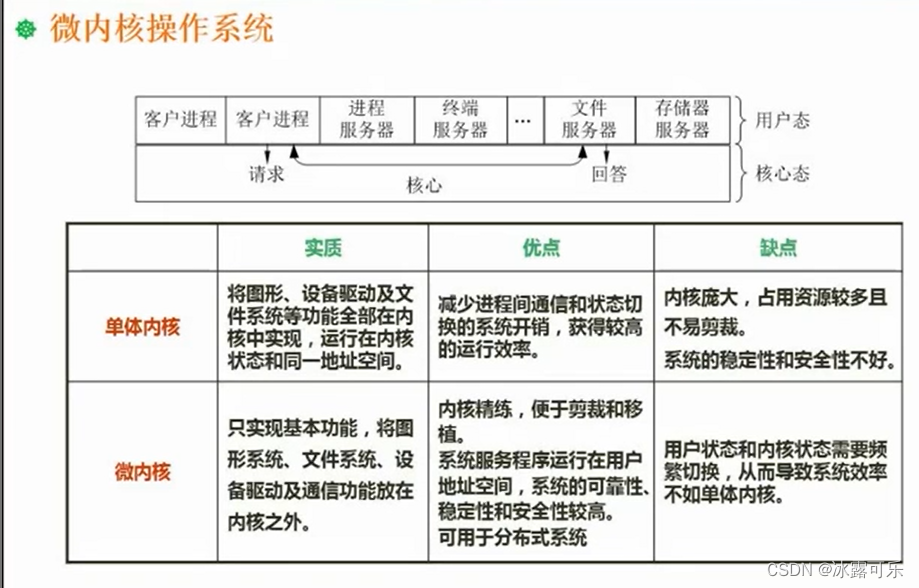
软考:中级软件设计师:文件管理,索引文件结构,树型文件结构,位示图,数据传输方式,微内核
软考:中级软件设计师: 提示:系列被面试官问的问题,我自己当时不会,所以下来自己复盘一下,认真学习和总结,以应对未来更多的可能性 关于互联网大厂的笔试面试,都是需要细心准备的 (1…...

实践-CNN卷积层
实践-CNN卷积层 1 卷积层构造2 整体流程3 BatchNormalization效果4 参数对比5 测试效果 1 卷积层构造 2 整体流程 根据网络结构来写就可以了。 池化 拉平 训练一个网络需要2-3天的时间。用经典网络来,一些细节没有必要去扣。 损失函数: fit模型&…...
【设计模式】MVC 模式
MVC 模式代表 Model-View-Controller(模型-视图-控制器) 模式。这种模式用于应用程序的分层开发。 Model(模型) - 模型代表一个存取数据的对象或 JAVA POJO。它也可以带有逻辑,在数据变化时更新控制器。Viewÿ…...

看康师傅金桔柠檬X国漫IP跨界出圈,打开IP合作新思路
Z世代年轻群体已经成为消费主力,其喜好和消费观念也呈现出全新态势。抓住年轻人的心,就是抓住了品牌未来的战场。 那么到底什么样的营销动作才能真正撬动年轻人? 对于互联网时代成长起来的Z世代年轻人来说,人气二次元IP无疑是能最…...
ElementUI的MessageBox的按钮置灰且不可点击
// this.$confirmthis.$alert(这是一段内容, 标题名称, {confirmButtonText: 确定,confirmButtonCLass: confirmButton,beforeClose: (action,instance,done) > {if (action confirm) {return false} else {done()}});}.confirmButton {background: #ccc !important;cursor…...

pc端与flutter通信失效, Method not found
报错情况描述:pc端与flutter通信,ios端能实现通信,安卓端通信报错 报错通信代码: //app消息通知window.callbackName function (res) {window?.jsBridge && window.jsBridge?.postMessage(JSON.stringify(res), "…...

linux 防火墙经常使用的命令
# 开启防火墙服务 systemctl start firewalld # 关闭防火墙服务 systemctl stop firewalld # 重启防火墙服务 systemctl restart firewalld # 开发端口 firewall-cmd --zonepublic --add-port8080/tcp --permanent # 移除端口 firewall-cmd --zonepublic --remove-port8080/tc…...

Docker desktop安装mysql
首先本地已经有 docker 环境存在,然后可以拉取 MySQL 镜像。 相关 mysql 仓库地址: https://hub.docker.com/_/mysql/ # 镜像拉取 docker pull mysql:8.0.26docker pull mysql:latest# 查看镜像列表docker image ls等待镜像完成之后就可以启动 mysql 了…...
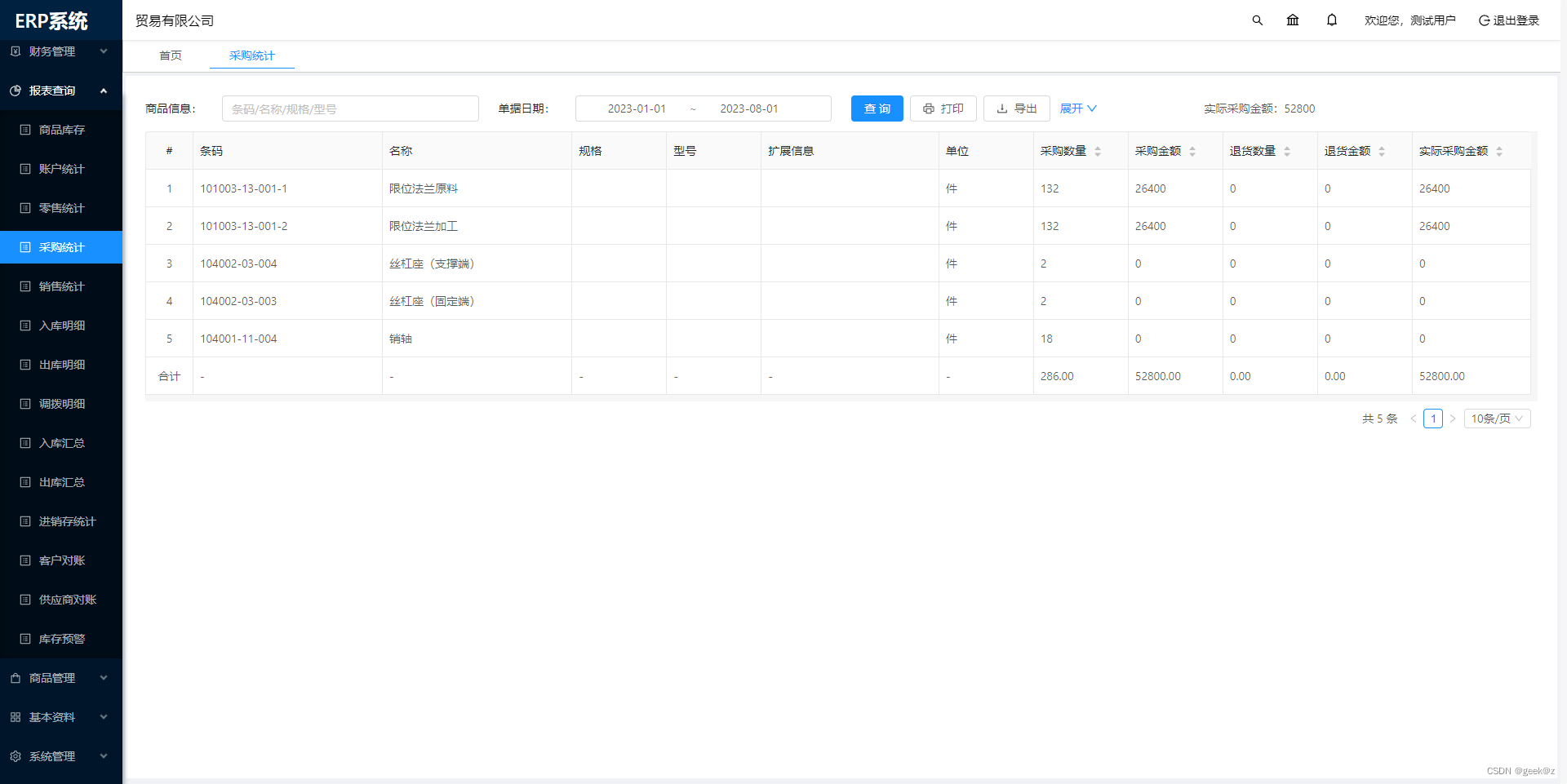
Java SpringBoot Vue ERP系统
系统介绍 该ERP系统基于SpringBoot框架和SaaS模式,支持多租户,专注进销存财务生产功能。主要模块有零售管理、采购管理、销售管理、仓库管理、财务管理、报表查询、系统管理等。支持预付款、收入支出、仓库调拨、组装拆卸、订单等特色功能。拥有商品库存…...

什么是CSS中的渐变(gradient)?如何使用CSS创建线性渐变和径向渐变?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 渐变(Gradient)在CSS中的应用⭐ 线性渐变(Linear Gradient)语法:示例: ⭐ 径向渐变(Radial Gradient)语法:示例: ⭐ 写…...

【深度学习】PyTorch快速入门
【深度学习】学习PyTorch基础 介绍PyTorch 深度学习框架是一种软件工具,旨在简化和加速构建、训练和部署深度学习模型的过程。深度学习框架提供了一系列的函数、类和工具,用于定义、优化和执行各种深度神经网络模型。这些框架帮助研究人员和开发人员专注…...

学习Vue:组件通信
组件化开发在现代前端开发中是一种关键的方法,它能够将复杂的应用程序拆分为更小、更可管理的独立组件。在Vue.js中,父子组件通信是组件化开发中的重要概念,同时我们还会讨论其他组件间通信的方式。 父子组件通信:Props 和 Events…...

springboot项目打包后读取jar包里面的
ResourcePatternResolver resourcePatternResolver new PathMatchingResourcePatternResolver(); Resource[] resources resourcePatternResolver.getResources("classpath*:templates/*.*"); for ( Resource resource : resources ) {//获取文件,在打成…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...
