算法leetcode|70. 爬楼梯(rust重拳出击)
文章目录
- 70. 爬楼梯:
- 样例 1:
- 样例 2:
- 提示:
- 分析:
- 题解:
- rust:
- go:
- c++:
- python:
- java:
70. 爬楼梯:
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
样例 1:
输入:n = 2输出:2解释:有两种方法可以爬到楼顶。1. 1 阶 + 1 阶2. 2 阶
样例 2:
输入:n = 3输出:3解释:有三种方法可以爬到楼顶。1. 1 阶 + 1 阶 + 1 阶2. 1 阶 + 2 阶3. 2 阶 + 1 阶
提示:
1 <= n <= 45
分析:
- 面对这道算法题目,二当家的再次陷入了沉思。
- 可以爬一阶或者两阶台阶,那也就是说,除了初始位置,和第一阶台阶,到达其他阶台阶
n的方式,就只能从n - 1阶台阶,或者n - 2阶台阶来。 - 这是典型的动态规划,到初始位置和第一阶台阶的方式只有一种,之后到达每一阶台阶的发方法总数都可以动态计算得来,即 f(x) = f(x − 1) + f(x − 2)。
- 动态规划方法我觉得很好了,但是由于有规律,用数学的方式计算,当然更快了,另外将前几项列出来,再结合定义,就会发现,到达每一阶台阶的方法总数恰好就是 斐波那契数列。
- 动态规划只能从
1到n按顺序推算,在n较大时,效率仍不令人满意,矩阵快速幂,可以有像二分查找一样的效率,数学的知识都还给老师了,有兴趣的可以去研究一下,能看明白,但是过段时间又会忘记,无奈啊,矩阵快速幂 是 矩阵乘法 和 快速幂 的结合,可以先分别了解,再结合理解。 - 所以建议一定要把动态规划优先掌握,其次是快速幂,至于通项公式,数学的方法,很难举一反三,要具体问题具体分析,说到底还是需要掌握数学知识本身,与君共勉。
- 最后,爬楼梯当然要5阶5阶的上才霸气。
题解:
rust:
impl Solution {pub fn climb_stairs(n: i32) -> i32 {let sqrt5 = 5f64.sqrt();let fibn = ((1f64 + sqrt5) / 2f64).powi(n + 1) - ((1f64 - sqrt5) / 2f64).powi(n + 1);return (fibn / sqrt5).round() as i32;}
}
go:
func climbStairs(n int) int {sqrt5 := math.Sqrt(5)pow1 := math.Pow((1+sqrt5)/2, float64(n+1))pow2 := math.Pow((1-sqrt5)/2, float64(n+1))return int(math.Round((pow1 - pow2) / sqrt5))
}
c++:
class Solution {
public:int climbStairs(int n) {const double sqrt5 = sqrt(5);const double fibn = pow((1 + sqrt5) / 2, n + 1) - pow((1 - sqrt5) / 2, n + 1);return (int) round(fibn / sqrt5);}
};
python:
class Solution:def climbStairs(self, n: int) -> int:sqrt5 = math.sqrt(5)fibn = pow((1 + sqrt5) / 2, n + 1) - pow((1 - sqrt5) / 2, n + 1)return round(fibn / sqrt5)java:
class Solution {public int climbStairs(int n) {final double sqrt5 = Math.sqrt(5);final double fibn = Math.pow((1 + sqrt5) / 2, n + 1) - Math.pow((1 - sqrt5) / 2, n + 1);return (int) Math.round(fibn / sqrt5);}
}
非常感谢你阅读本文~
欢迎【点赞】【收藏】【评论】三连走一波~
放弃不难,但坚持一定很酷~
希望我们大家都能每天进步一点点~
本文由 二当家的白帽子:https://le-yi.blog.csdn.net/ 博客原创~
相关文章:
)
算法leetcode|70. 爬楼梯(rust重拳出击)
文章目录 70. 爬楼梯:样例 1:样例 2:提示: 分析:题解:rust:go:c:python:java: 70. 爬楼梯: 假设你正在爬楼梯。需要 n 阶你才能到达楼…...
)
基于epoll的TCP服务器端(C++)
网络编程——C实现socket通信(TCP)高并发之epoll模式_tcp通信c 多客户端epoll_n大橘为重n的博客-CSDN博客 网络编程——C实现socket通信(TCP)高并发之select模式_n大橘为重n的博客-CSDN博客 server.cpp #include <stdio.h> #include <sys/types.h> #include <…...

实时安全分析监控加强网络安全
网络犯罪分子只需几分钟,有时甚至几秒钟即可泄露敏感数据。但是,IT 团队可能无法在数周内发现这些违规行为。通常,这些违规行为是由外部方或客户发现的,到那时为时已晚。随着网络漏洞的激增,对安全分析的需求空前高涨。…...

基于ipad协议的gewe框架进行微信群组管理(二)
友情链接 geweapi.com 点击访问即可。 获取群组详情 小提示: 该接口可以一次查询20个群组查询出来的信息是不带公告的 请求URL: http://域名地址/api/group/detail 请求方式: POST 请求头: Content-Type:applica…...
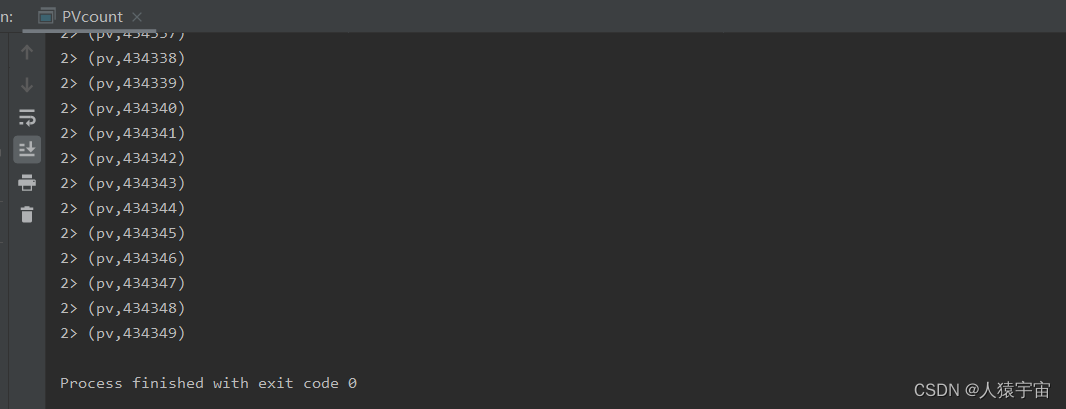
大数据-玩转数据-Flink网页埋点PV统计
一、说明 衡量网站流量一个最简单的指标,就是网站的页面浏览量(Page View,PV)。用户每次打开一个页面便记录1次PV,多次打开同一页面则浏览量累计。 一般来说,PV与来访者的数量成正比,但是PV并不…...

什么是伪类选择器?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 伪类选择器⭐ 一些常见的伪类选择器示例::hover:active:focus:nth-child(n):first-child 和 :last-child ⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦 几何…...
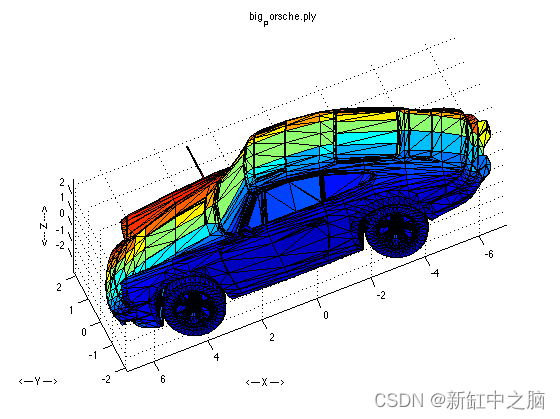
PLY模型格式详解【3D】
本文介绍PLY 多边形文件格式,这是一种用于存储被描述为多边形集合的图形对象。 PLY文件格式的目标是提供一种简单且易于实现但通用的格式足以适用于各种模型。 PLY有两种子格式:易于入门的 ASCII 表示形式和用于紧凑存储和快速保存和加载的二进制格式。 …...

Java的反射机制、Lambda表达式和枚举
Java的反射机制、Lambda表达式和枚举 文章目录 Java的反射机制、Lambda表达式和枚举1.反射机制反射的概念、用途、优缺点反射相关的类及使用(重要!!)相关类Class类:代表类实体,表示类和接口Field类…...
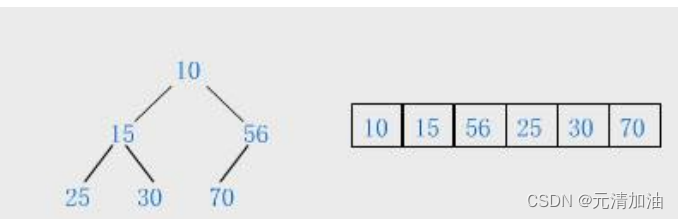
数据结构:堆的实现
1.堆的概念 如果有一个关键码的集合 K { k1 ,k2 ,k3 ,…,kn },把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并且 k(i) < k(i*21) 和 k(i) < k(i*22), i 0 ÿ…...
zabbix-6.4 监控 MySQL
目录 1、rpm安装zabbix_agentd服务 2、编写zabbix_agentd.conf文件 3、编写模板文件 4、创建mysql用户并赋权限 5、创建.my.cnf文件 6、将规则添加到SELinux策略中 注意: 若模板无法读取.my.cnf 信息,从而导致监控报错,可以尝试修改模…...
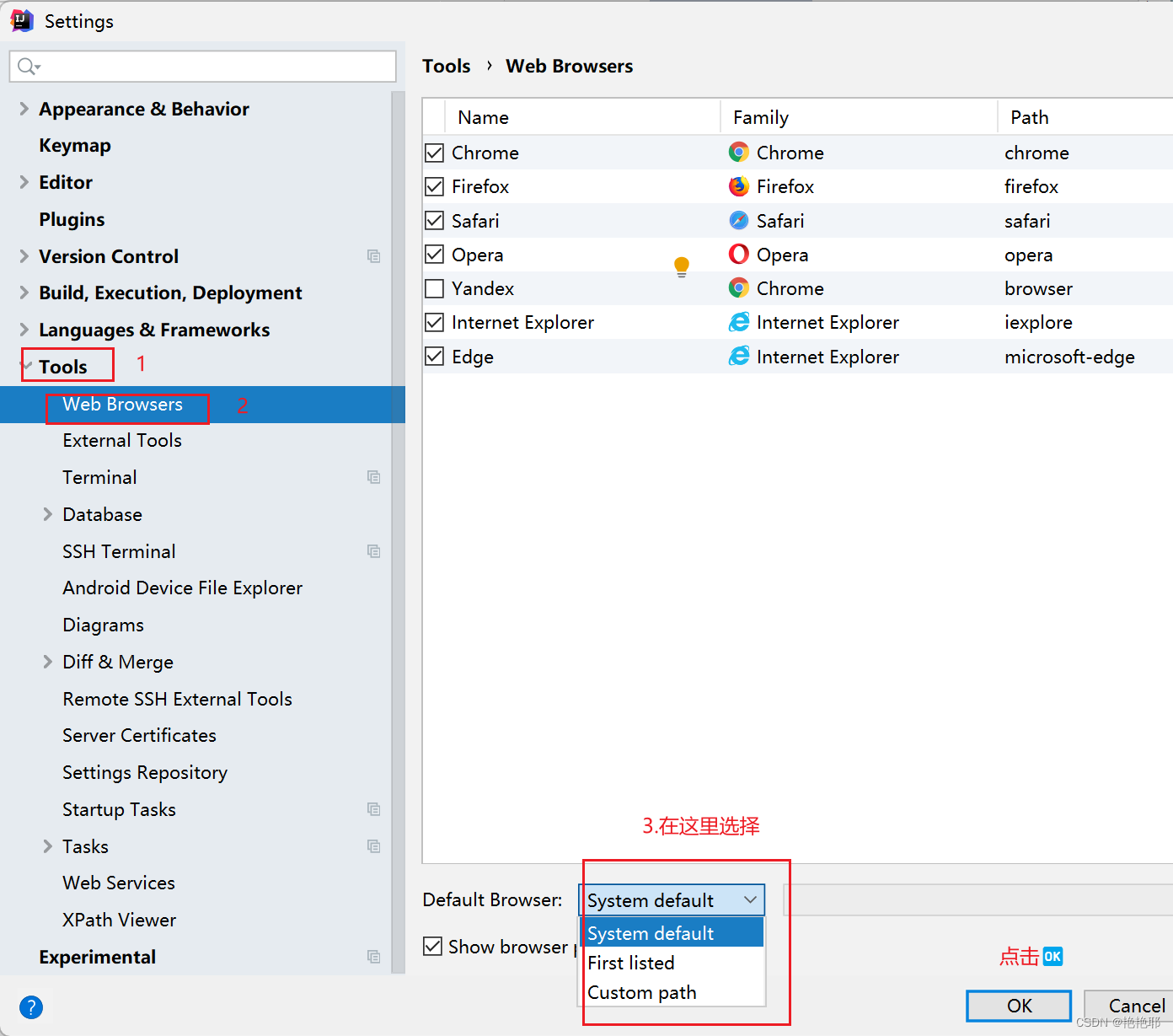
深入探索:解读创意的力量——idea的下载、初步使用
目录 编辑 1.IDEA的简介 2.IDEA的下载 2.1下载路径https://www.jetbrains.com/zh-cn/idea/download/?sectionwindows编辑 2.2下载的步骤 3 idea的初步使用 3.1新建一个简单的Java项目 3.1.1首先需要创建一个新的工程 3.1.2创建一个新的项目(模块&am…...

Redis详解
Redis 简介 Redis(Remote Dictionary Server)是一个开源的高性能键值对存储数据库,最初由 Salvatore Sanfilippo 开发,它在内存中存储数据,并提供了持久化功能,可以将数据保存到磁盘中,是一种N…...
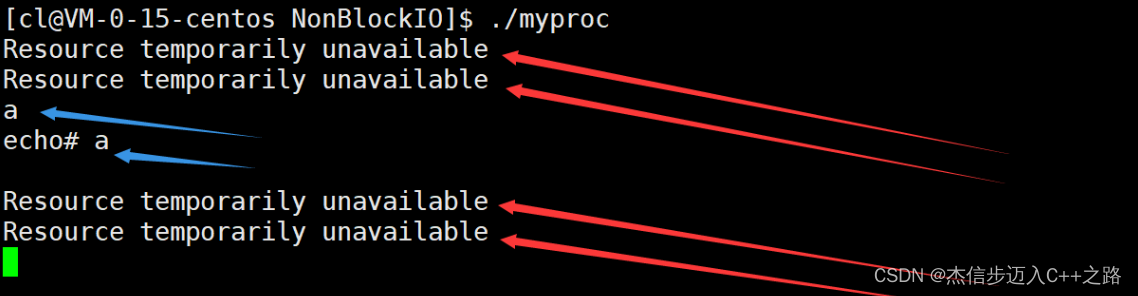
【Linux】高级IO
目录 IO的基本概念 钓鱼五人组 五种IO模型 高级IO重要概念 同步通信 VS 异步通信 阻塞 VS 非阻塞 其他高级IO 阻塞IO 非阻塞IO IO的基本概念 什么是IO? I/O(input/output)也就是输入和输出,在著名的冯诺依曼体系结构当中…...

动态HTTP代理与竞争情报收集的关联
Hey,各位爬友们!作为一名专业的爬虫HTTP代理提供者,今天我要和大家聊一聊动态HTTP代理与竞争情报收集之间的关联。在这篇文章中,我将向大家解释怎么使用动态HTTP代理完成在竞争中的情报收集,并分享一些实用的技巧。 首…...
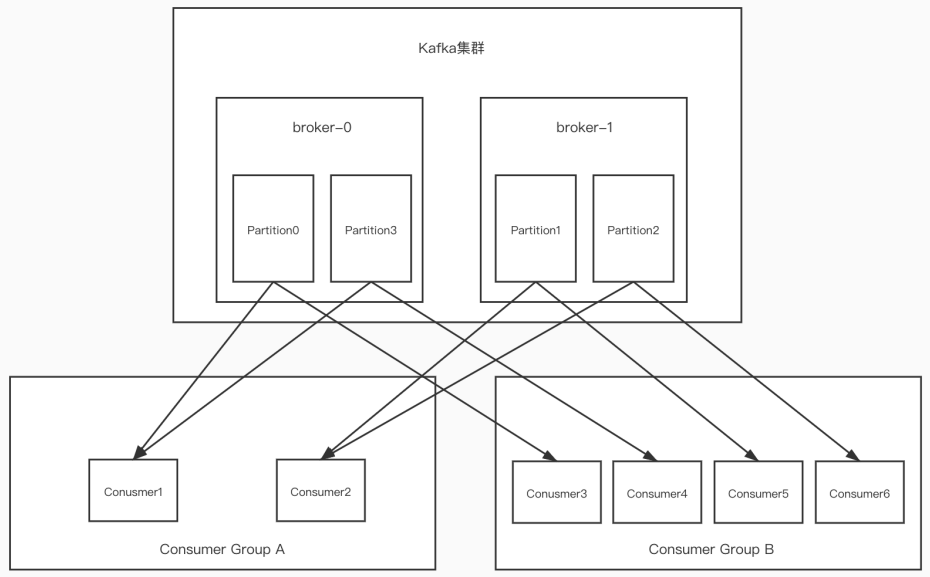
kafka基本概念及操作
kafka介绍 Kafka是最初由Linkedin公司开发,是一个分布式、支持分区的(partition)、多副本的 (replica),基于zookeeper协调的分布式消息系统,它的最大的特性就是可以实时的处理大量数据以满足各…...

分享个试卷去笔迹什么软件,几个步骤轻松擦除
试卷擦去笔迹是一项非常关键的技能,它可以帮助你更好地管理你的笔记和文件。不管是小伙伴们想重新测试试卷或者是将试卷输出为电子版,都可以实现的。在这篇文章中,我将分享一些方法和软件,帮助你更好地进行试卷擦除。有需要的小伙…...

ClickHouse(十八):Clickhouse Integration系列表引擎
进入正文前,感谢宝子们订阅专题、点赞、评论、收藏!关注IT贫道,获取高质量博客内容! 🏡个人主页:含各种IT体系技术,IT贫道_Apache Doris,大数据OLAP体系技术栈,Kerberos安全认证-CSDN博客 &…...

日常BUG——代码提交到了本地但是没有push,删除了本地分支如何恢复
😜作 者:是江迪呀✒️本文关键词:日常BUG、BUG、问题分析☀️每日 一言 :存在错误说明你在进步! 一、问题描述 代码在本地提交了,但是没有push到远程,然后删除了本地的分支。想要恢…...
Markdown语法
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 Markdown语法目录 前言1.标题2.文本样式3.列表四.图片5.链接6.目录7.代码片7.表格8.注脚9.注释10.自定义列表11.LaTeX数学公式12.插入甘特图13.插入UML图14.插入Merimaid流程…...

vue3表格,编辑案例
index.vue <script setup> import { onMounted, ref } from "vue"; import Edit from "./components/Edit.vue"; import axios from "axios";// TODO: 列表渲染 const list ref([]); const getList async () > {const res await ax…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

大数据治理的常见方式
大数据治理的常见方式 大数据治理是确保数据质量、安全性和可用性的系统性方法,以下是几种常见的治理方式: 1. 数据质量管理 核心方法: 数据校验:建立数据校验规则(格式、范围、一致性等)数据清洗&…...

JS红宝书笔记 - 3.3 变量
要定义变量,可以使用var操作符,后跟变量名 ES实现变量初始化,因此可以同时定义变量并设置它的值 使用var操作符定义的变量会成为包含它的函数的局部变量。 在函数内定义变量时省略var操作符,可以创建一个全局变量 如果需要定义…...
