[Poetize6] IncDec Sequence
题目描述
给定一个长度为 n 的数列 a_1,a_2,...,a_n,每次可以选择一个区间[l,r],使这个区间内的数都加 1 或者都减 1。
请问至少需要多少次操作才能使数列中的所有数都一样,并求出在保证最少次数的前提下,最终得到的数列有多少种。
输入格式
第一行一个正整数 n
接下来 n 行,每行一个整数,第 i+1 行的整数表示 a_i。
输出格式
第一行输出最少操作次数
第二行输出最终能得到多少种结果
样例 #1
样例输入 #1
4
1
1
2
2
样例输出 #1
1
2
提示
对于 100% 的数据,n<= 100000, 0 <= a_i <= 2^31。
代码:
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long LL; // 定义 long long 类型的别名为 LL
LL n, c, p, q, a[100010]; // 声明变量int main()
{cin >> n; // 输入数组的长度 nfor (int i = 1; i <= n; i++){scanf("%lld", &a[i]); // 输入数组的元素}for (int i = 2; i <= n; i++) // 从第二个元素开始遍历数组{c = a[i] - a[i - 1]; // 计算相邻元素之间的差值if (c > 0) // 如果差值大于 0,说明需要增加操作{p += c; // 累加增加操作次数}else // 否则,需要减少操作{q -= c; // 取反后累加减少操作次数}}LL ans1 = max(p, q); // 找到增加和减少操作次数中的较大值,作为最少操作次数LL ans2 = abs(p - q) + 1; // 计算操作次数之差的绝对值加 1,作为最终可能的结果种数cout << ans1 << endl << ans2; // 输出最少操作次数和结果种数return 0; // 程序结束
}
相关文章:

[Poetize6] IncDec Sequence
题目描述 给定一个长度为 n 的数列 a_1,a_2,...,a_n,每次可以选择一个区间[l,r],使这个区间内的数都加 1 或者都减 1。 请问至少需要多少次操作才能使数列中的所有数都一样,并求出在保证最少次数的前提下,最终得到的数列有多…...
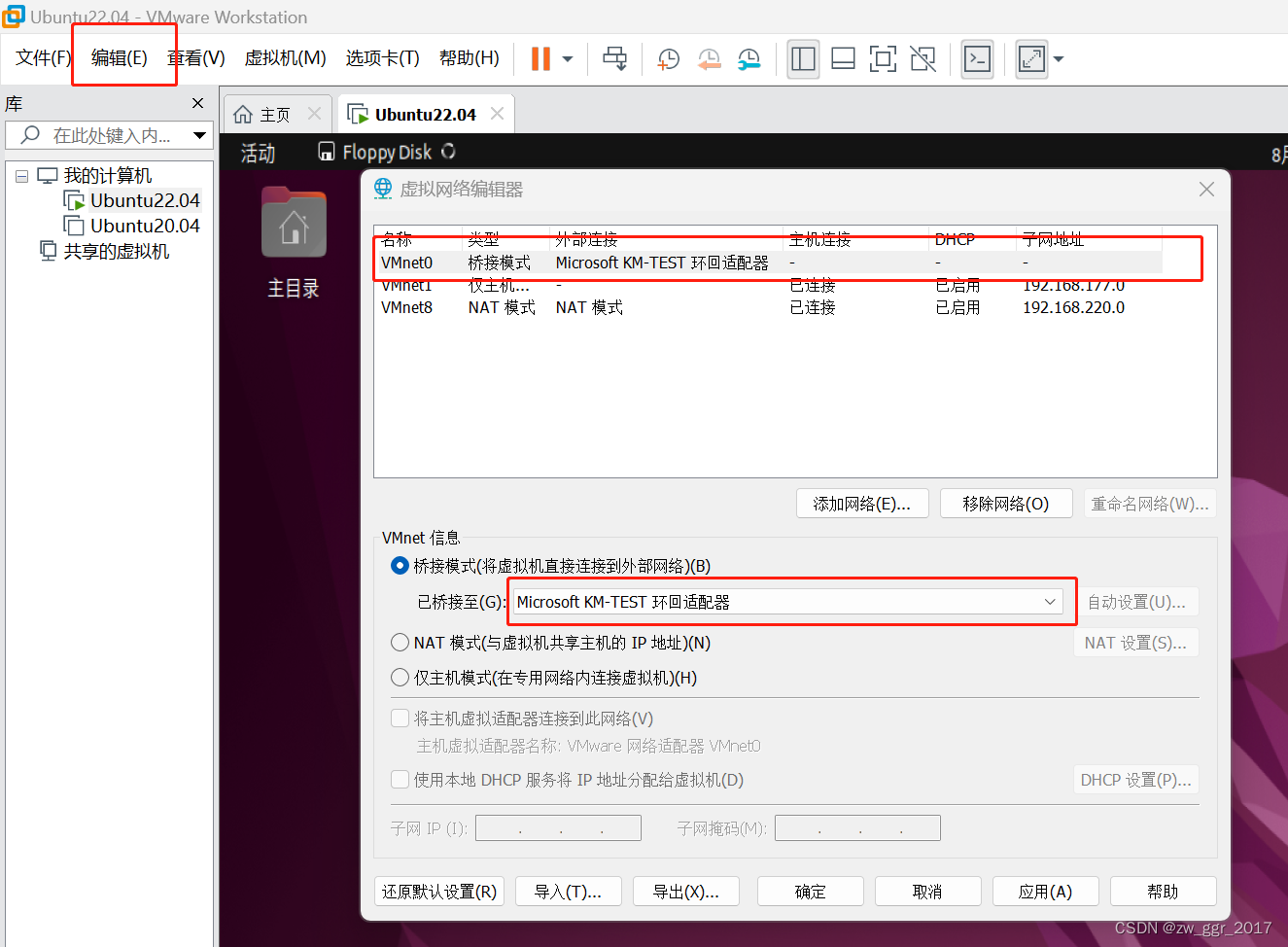
通过Microsoft Loopback Adapter实现虚拟机和物理机的通信
问题 问:不借助路由器或交换机的情况下,能不能实现主机和虚拟及之间两个软件的通信呢?要求主机和虚拟及均有独立的ip地址,从而进行指定源的组播通信。 答:可以。通过借助虚拟网络适配器,不需要路由器或交…...
)
算法leetcode|70. 爬楼梯(rust重拳出击)
文章目录 70. 爬楼梯:样例 1:样例 2:提示: 分析:题解:rust:go:c:python:java: 70. 爬楼梯: 假设你正在爬楼梯。需要 n 阶你才能到达楼…...
)
基于epoll的TCP服务器端(C++)
网络编程——C实现socket通信(TCP)高并发之epoll模式_tcp通信c 多客户端epoll_n大橘为重n的博客-CSDN博客 网络编程——C实现socket通信(TCP)高并发之select模式_n大橘为重n的博客-CSDN博客 server.cpp #include <stdio.h> #include <sys/types.h> #include <…...

实时安全分析监控加强网络安全
网络犯罪分子只需几分钟,有时甚至几秒钟即可泄露敏感数据。但是,IT 团队可能无法在数周内发现这些违规行为。通常,这些违规行为是由外部方或客户发现的,到那时为时已晚。随着网络漏洞的激增,对安全分析的需求空前高涨。…...

基于ipad协议的gewe框架进行微信群组管理(二)
友情链接 geweapi.com 点击访问即可。 获取群组详情 小提示: 该接口可以一次查询20个群组查询出来的信息是不带公告的 请求URL: http://域名地址/api/group/detail 请求方式: POST 请求头: Content-Type:applica…...
大数据-玩转数据-Flink网页埋点PV统计
一、说明 衡量网站流量一个最简单的指标,就是网站的页面浏览量(Page View,PV)。用户每次打开一个页面便记录1次PV,多次打开同一页面则浏览量累计。 一般来说,PV与来访者的数量成正比,但是PV并不…...

什么是伪类选择器?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 伪类选择器⭐ 一些常见的伪类选择器示例::hover:active:focus:nth-child(n):first-child 和 :last-child ⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦 几何…...
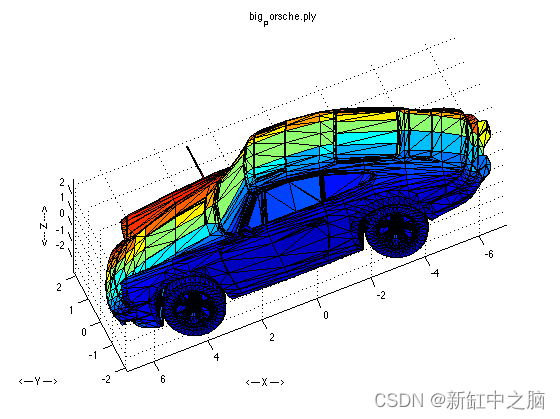
PLY模型格式详解【3D】
本文介绍PLY 多边形文件格式,这是一种用于存储被描述为多边形集合的图形对象。 PLY文件格式的目标是提供一种简单且易于实现但通用的格式足以适用于各种模型。 PLY有两种子格式:易于入门的 ASCII 表示形式和用于紧凑存储和快速保存和加载的二进制格式。 …...

Java的反射机制、Lambda表达式和枚举
Java的反射机制、Lambda表达式和枚举 文章目录 Java的反射机制、Lambda表达式和枚举1.反射机制反射的概念、用途、优缺点反射相关的类及使用(重要!!)相关类Class类:代表类实体,表示类和接口Field类…...
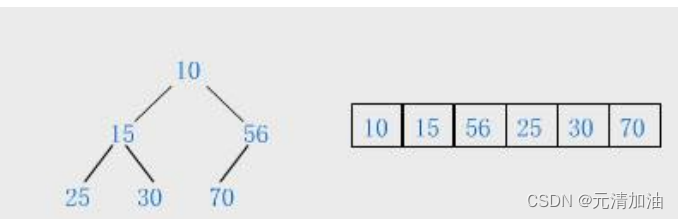
数据结构:堆的实现
1.堆的概念 如果有一个关键码的集合 K { k1 ,k2 ,k3 ,…,kn },把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并且 k(i) < k(i*21) 和 k(i) < k(i*22), i 0 ÿ…...
zabbix-6.4 监控 MySQL
目录 1、rpm安装zabbix_agentd服务 2、编写zabbix_agentd.conf文件 3、编写模板文件 4、创建mysql用户并赋权限 5、创建.my.cnf文件 6、将规则添加到SELinux策略中 注意: 若模板无法读取.my.cnf 信息,从而导致监控报错,可以尝试修改模…...
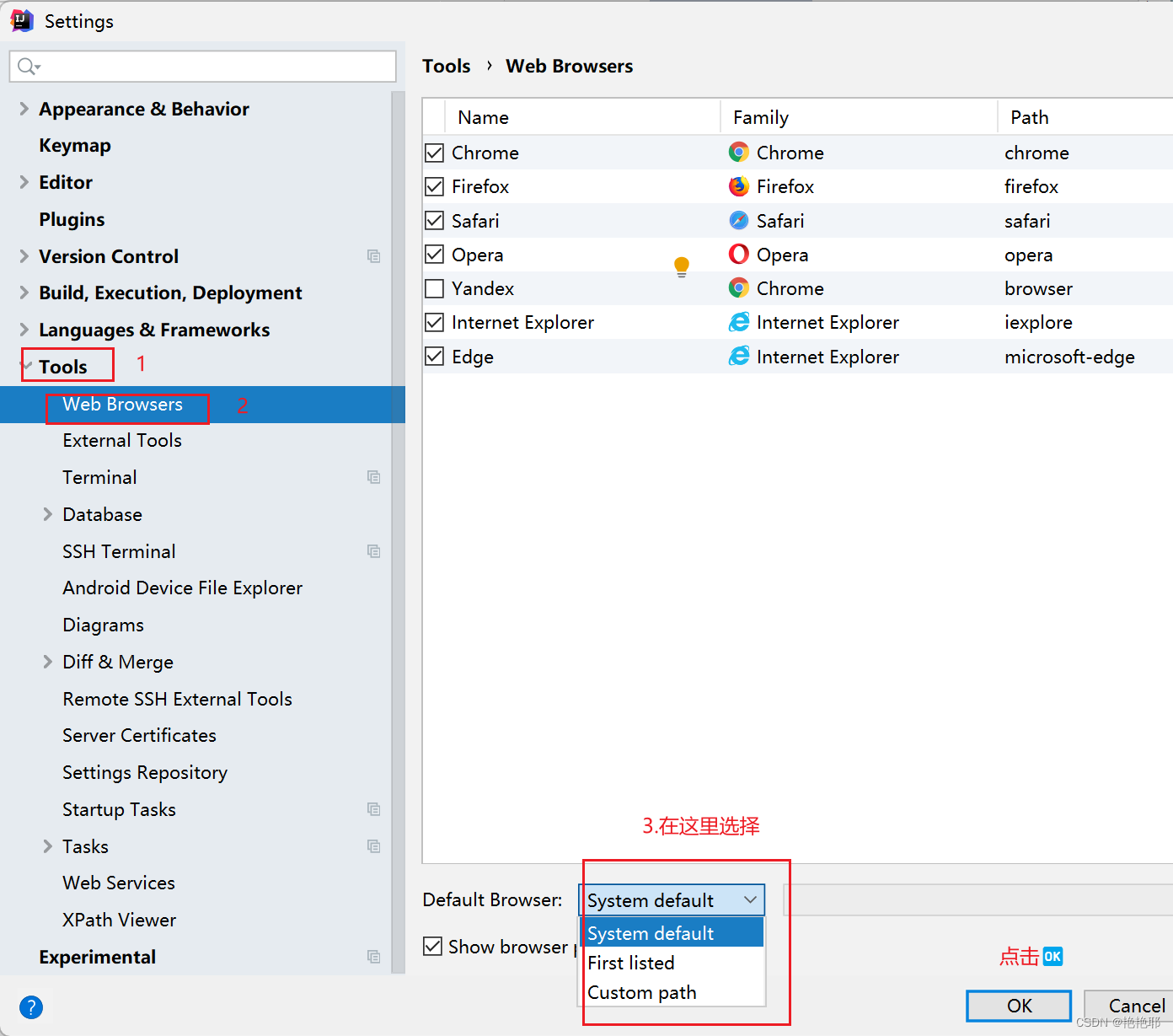
深入探索:解读创意的力量——idea的下载、初步使用
目录 编辑 1.IDEA的简介 2.IDEA的下载 2.1下载路径https://www.jetbrains.com/zh-cn/idea/download/?sectionwindows编辑 2.2下载的步骤 3 idea的初步使用 3.1新建一个简单的Java项目 3.1.1首先需要创建一个新的工程 3.1.2创建一个新的项目(模块&am…...

Redis详解
Redis 简介 Redis(Remote Dictionary Server)是一个开源的高性能键值对存储数据库,最初由 Salvatore Sanfilippo 开发,它在内存中存储数据,并提供了持久化功能,可以将数据保存到磁盘中,是一种N…...
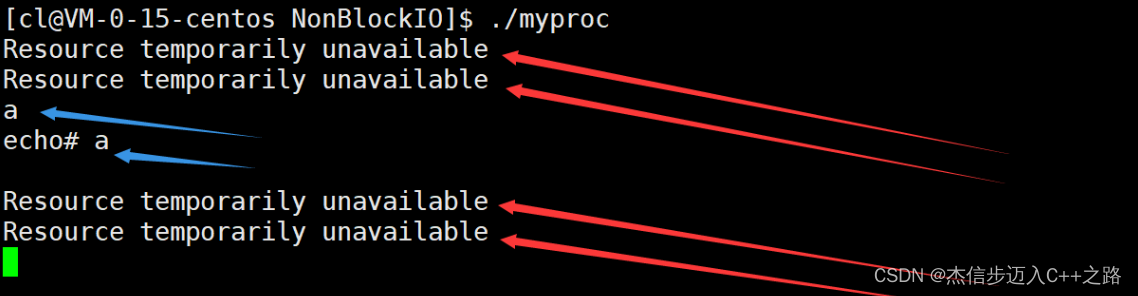
【Linux】高级IO
目录 IO的基本概念 钓鱼五人组 五种IO模型 高级IO重要概念 同步通信 VS 异步通信 阻塞 VS 非阻塞 其他高级IO 阻塞IO 非阻塞IO IO的基本概念 什么是IO? I/O(input/output)也就是输入和输出,在著名的冯诺依曼体系结构当中…...

动态HTTP代理与竞争情报收集的关联
Hey,各位爬友们!作为一名专业的爬虫HTTP代理提供者,今天我要和大家聊一聊动态HTTP代理与竞争情报收集之间的关联。在这篇文章中,我将向大家解释怎么使用动态HTTP代理完成在竞争中的情报收集,并分享一些实用的技巧。 首…...
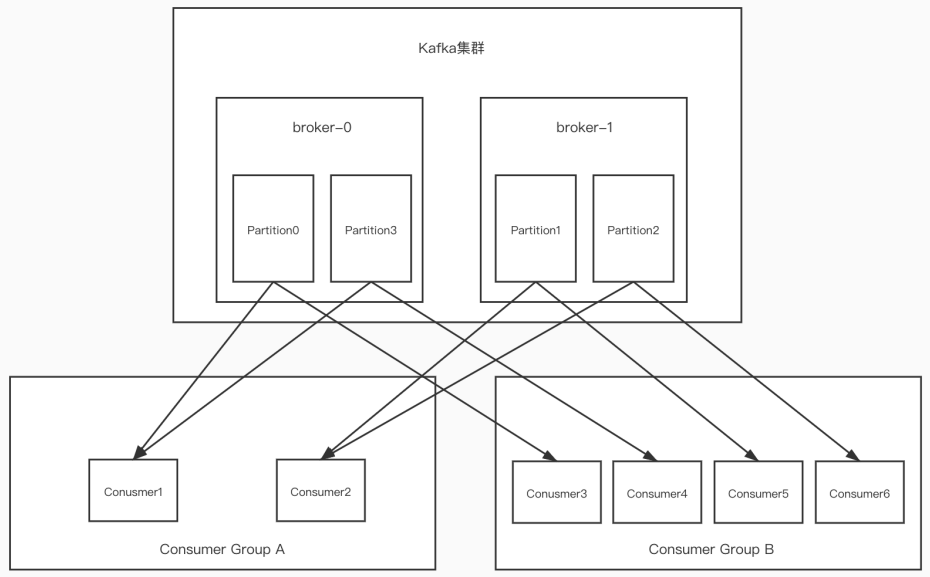
kafka基本概念及操作
kafka介绍 Kafka是最初由Linkedin公司开发,是一个分布式、支持分区的(partition)、多副本的 (replica),基于zookeeper协调的分布式消息系统,它的最大的特性就是可以实时的处理大量数据以满足各…...

分享个试卷去笔迹什么软件,几个步骤轻松擦除
试卷擦去笔迹是一项非常关键的技能,它可以帮助你更好地管理你的笔记和文件。不管是小伙伴们想重新测试试卷或者是将试卷输出为电子版,都可以实现的。在这篇文章中,我将分享一些方法和软件,帮助你更好地进行试卷擦除。有需要的小伙…...

ClickHouse(十八):Clickhouse Integration系列表引擎
进入正文前,感谢宝子们订阅专题、点赞、评论、收藏!关注IT贫道,获取高质量博客内容! 🏡个人主页:含各种IT体系技术,IT贫道_Apache Doris,大数据OLAP体系技术栈,Kerberos安全认证-CSDN博客 &…...

日常BUG——代码提交到了本地但是没有push,删除了本地分支如何恢复
😜作 者:是江迪呀✒️本文关键词:日常BUG、BUG、问题分析☀️每日 一言 :存在错误说明你在进步! 一、问题描述 代码在本地提交了,但是没有push到远程,然后删除了本地的分支。想要恢…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...
