每天一个知识点——L2R
面试的时候,虽然做过医疗文献搜索,也应用过L2R的相关模型,但涉及到其中的一些技术细节,都会成为我拿不下offer永远的痛。也尝试过去理解去背下一些知识点,终究没有力透纸背,随着时间又开始变得模糊,下面对相关问题进行一个总结。
一、PointWise、PairWise和ListWise
这个并不是特定的算法,而是排序模型的设计思路,主要体现在损失函数(Loss Function)以及相应的标签标注方式和优化方法的不同。
PointWise
可以训练一个二分类网络:,其中
。训练的目标是最小化数据集中所有问题和候选句子对的交叉熵。
缺陷是虽然预测分数,但损失函数只考虑正负样本,并不要求精确打分,正样本内的先后关系并不在考虑范围。
Pointwise常见算法有SVM等
PairWise
损失函数为合页损失函数:
这里m为边界阈值,即正样本的得分不仅要比负样本的高,而且还要高出一定阈值范围,。
缺陷是对噪音更加敏感,比如一个样本标注错误,会引起多个pair对错误,仅考虑了pair对的相对位置信息,并没有考虑到绝对位置信息。
Pairwise常见算法有Ranking SVM、RankNet、RankBoost等。
ListWise
在训练过程中给定提问和它的一系列候选句子
和标签
,归一化的得分向量
通过如下公式计算:
标签归一化为,
训练的目标可以为最小化和
的KL散度。
Listwise常见算法有AdaRank,SoftRank,LambdaMART等
二、RankNet、LambdaRank和LambdaMart
RankNet
RankNet的训练数据是一个个的pair对,比如文章(i,j),然后模型对两个候选进行打分,我们建模的目标是一个概率,即模型认为候选i比候选j更相关的概率:
,
LambdaRank
首先对RankNet的损失函数进行分解,得到其中的梯度,
可以表示梯度的强度,进一步简化,假设对于文档对(i,j),都有文档i在文档j前面,即
,则
LambdaRank主要创新点在于不直接定义模型的损失函数再求梯度,而是通过分析RankNet排序损失函数的梯度再直接对梯度lambda进行修改。
现在将NDCG,ERR等指标引入lambda中,论文中的做法是交换两个文档i,j的位置,然后计算评估指标的变化情况,把
作为lambda的因子,Z可以是NDCG等评价指标
通过梯度lambda也可以反推出LambdaRank的损失函数,如下,
三、LambdaMart的实现原理
MART: Multiple Additive Regression Tree
GBDT: Gradient Boosting Decision Tree
- 基于多个决策树来预测结果;
- 决策树之间通过加法模型叠加结果;
- 每棵决策树都是针对之前决策树的不足进行改进。

综上的伪代码可知,lambdaMart的计算经历这样几个步骤
- 利用训练数据每个query的pair对情况,计算
,
同时,计算的,还有权重参数,用于牛顿迭代法,但实际代码中感觉没有用到这一块。
2. 以每个样本特征为,以
为拟合目标
,构建决策树,
3. 然后用训练的决策树去预测的分数,将得到分数加入
中,
4、然后重复上面3个步骤,训练多棵决策树。
说到决策树的训练:lambdaMART采用最朴素的最小二乘法,也就是最小化平方误差和来分裂节点:即对于某个选定的feature,选定一个值val,所有<=val的样本分到左子节点,>val的分到右子节点。然后分别对左右两个节点计算平方误差和,并加在一起作为这次分裂的代价。遍历所有feature以及所有可能的分裂点val(每个feature按值排序,每个不同的值都是可能的分裂点),在这些分裂中找到代价最小的。
五、评价指标
NDCG
这里计算的时候,会可能会采取两种策略,需要注意下:
1、预测结果的分数不要,只要文档的顺序,而具体分数用文档真实的分数,也就是分子分母计算的用的是同一套,只不过由于预测文档的先后顺序出现变动,最大分数未必会出现在第一位;
2、分子用预测分数,分母用真实分数。
另外需要注意的一点是分子分母计算面对可能并非完全一样的样本集。
六、参考文献
-
排序学习(LTR)经典算法:RankNet、LambdaRank和LambdaMart
- LambdaMART简介-基于Ranklib源码(Regression Tree训练)
- LambdaMART简介-基于Ranklib源码(lambda计算)
相关文章:
每天一个知识点——L2R
面试的时候,虽然做过医疗文献搜索,也应用过L2R的相关模型,但涉及到其中的一些技术细节,都会成为我拿不下offer永远的痛。也尝试过去理解去背下一些知识点,终究没有力透纸背,随着时间又开始变得模糊…...

解决flutter showDialog下拉框,复选框等无法及时响应的问题
使用StatefulBuilder _showDialogr() {showDialog(context: context,builder: (BuildContext ctx) {return StatefulBuilder(builder: (BuildContext context, StateSetter setState) {return Scaffold(body: Column(children: <Widget>[Container(height: 400,padding: …...
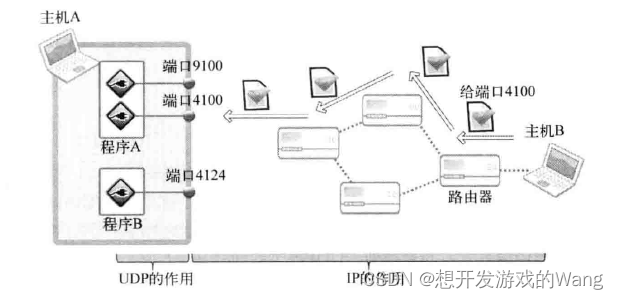
[C++ 网络协议编程] UDP协议
目录 1. UDP和TCP的区别 2. UDP的工作原理 3. UDP存在数据边界 4. UDP的I/O函数 4.1 sendto函数 4.2 recvfrom函数 4. 已连接(connected)UDP套接字和未连接(unconnected)UDP套接字 5. UDP的通信流程 5.1 服务器端通信流程 5.2 客户端通信流程 1. UDP和TCP的区别 主要…...
)
reactNative跳转appstore链接报错:Redirection to URL with a scheme that is not HTTP(S)
在reactnative中webview跳转H5下载页面,包错Redirection to URL with a scheme that is not HTTP(S) 在webview中添加一下代码 const onShouldStartLoadWithRequest (event: any) > {const { url } event;console.log(url);if (url.startsWith(https://itune…...

html css实现爱心
<!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>Document</title><style>/* 爱心 */.lo…...

react中使用shouldComponentUpdate生命周期函数调用setState引起的无限循环的错误
场景: 在 React 组件中,当在 componentWillUpdate 或 componentDidUpdate 生命周期方法中调用 setState 时,会触发无限循环,导致超过最大更新深度。 错误原因 在React组件中 ,我们使用componentWillUpdate 或 componen…...

麦肯锡发布《2023科技趋势展望报告》,生成式AI、下一代软件开发成为趋势,软件测试如何贴合趋势?
近日,麦肯锡公司发布了《2023科技趋势展望报告》。报告列出了15个趋势,并把他们分为5大类,人工智能革命、构建数字未来、计算和连接的前沿、尖端工程技术和可持续发展。 类别一:人工智能革命 生成式AI 生成型人工智能标志着人工智…...
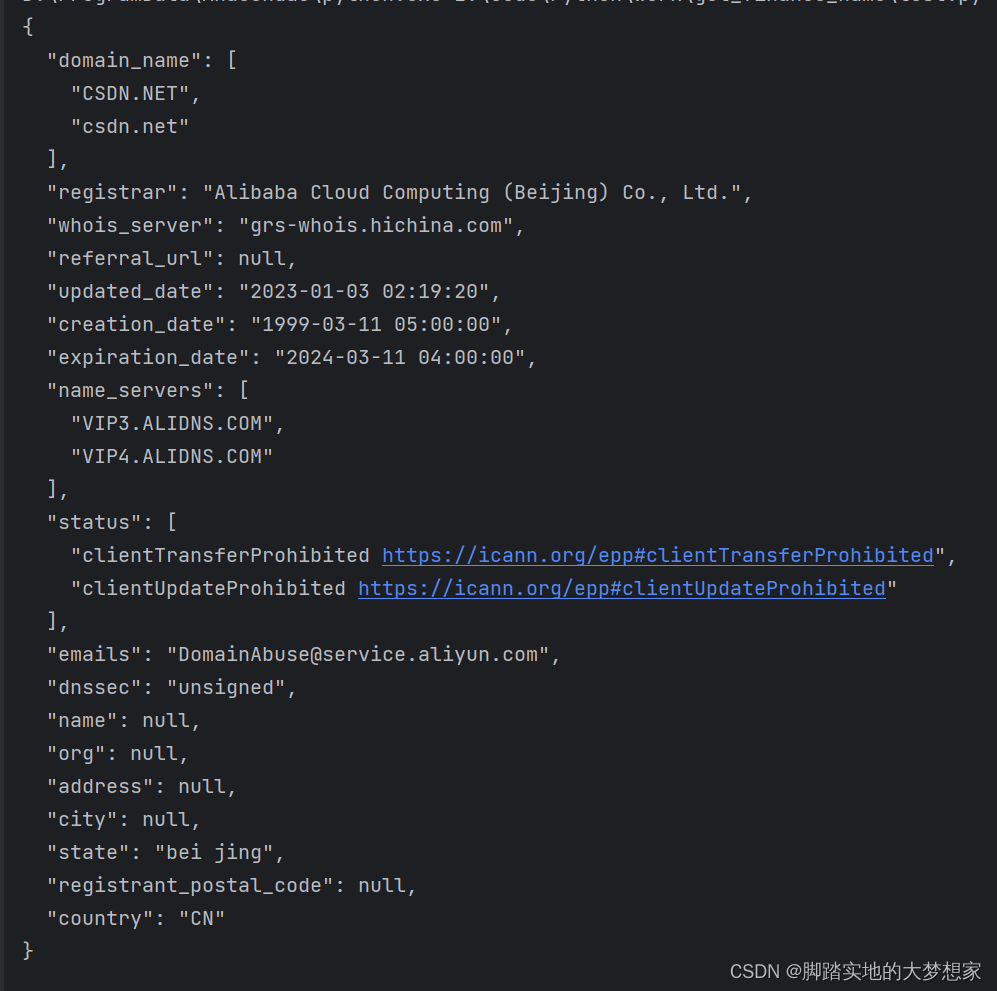
【爬虫】P1 对目标网站的背景调研(robot.txt,advanced_search,builtwith,whois)
对目标网站的背景调研 检查 robot.txt估算网站大小识别网站所用技术寻找网站的所有者 检查 robot.txt 目的: 大多数的网站都会包含 robot.txt 文件。该文件用于指出使用爬虫爬取网站时有哪些限制。而我们通过读 robot.txt 文件,亦可以最小化爬虫被封禁的…...
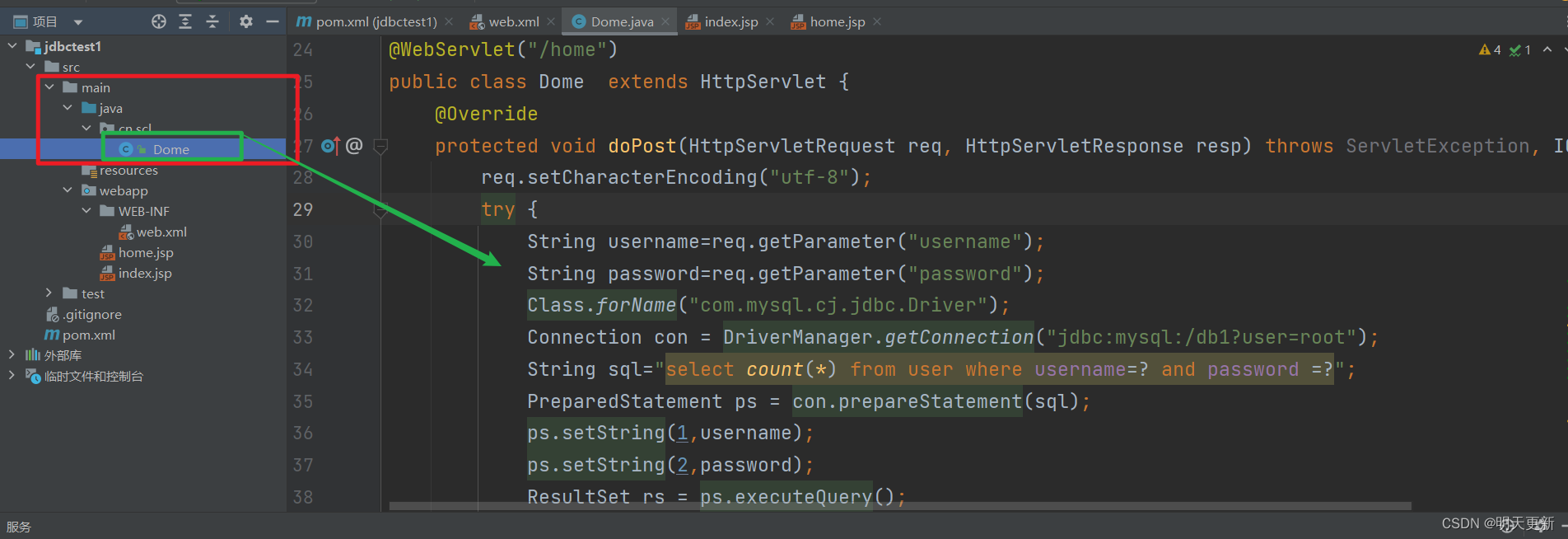
maven如何建立JavaWeb项目并连接数据库,验证登录
这里是建立建立web项目:Maven如何创建Java web项目(纯干货版)!!!_明天更新的博客-CSDN博客 我们主要演示如何连接数据库验证登录。 1.在webapp目录下创建我们的登录页面:index.jsp 还需要再…...

CVPR 2023 | 用户可控的条件图像到视频生成方法(基于Diffusion)
注1:本文系“计算机视觉/三维重建论文速递”系列之一,致力于简洁清晰完整地介绍、解读计算机视觉,特别是三维重建领域最新的顶会/顶刊论文(包括但不限于 Nature/Science及其子刊; CVPR, ICCV, ECCV, NeurIPS, ICLR, ICML, TPAMI, IJCV 等)。 本次介绍的论…...
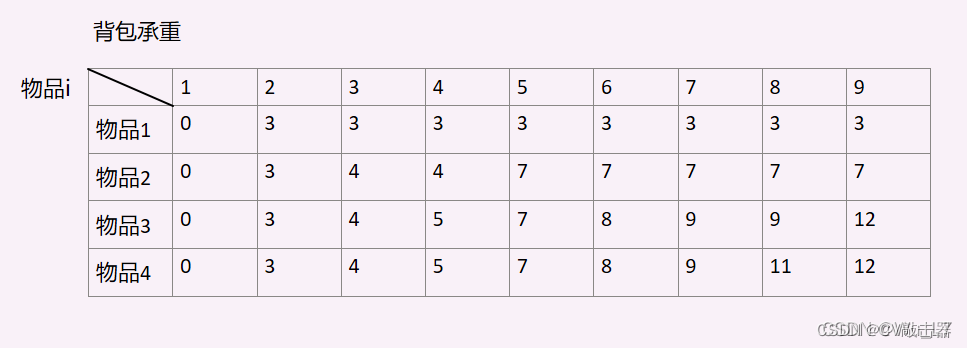
动态规划(基础)
一,背包问题 老规矩,上链接(http://t.csdn.cn/hEwvu) (1)01背包问题 给定一个承重量为C的背包,n个重量分别为w1,w2,...,wn的物品,物品i放入背包能产生pi(>0)的价值(i1,…...

【Pytorch:nn.Embedding】简介以及使用方法:用于生成固定数量的具有指定维度的嵌入向量embedding vector
文章目录 1、nn.Embedding2、使用场景 1、nn.Embedding 首先我们讲解一下关于嵌入向量embedding vector的概念 1)在自然语言处理NLP领域,是将单词、短语或其他文本单位映射到一个固定长度的实数向量空间中。嵌入向量具有较低的维度,通常在几…...

动态库的命名规则
1、动态库的命名规则:libname.so.x.y.z 名字含义lib这是共享库的前缀name共享库名字x主版本号y次版本号z发布版本号 2、每个版本号的含义 版本号含义主版本号表示库的重大升级,不同主版本号的库之间是不兼容的。依赖旧的主版本号的程序需要改动相应的…...

【Linux】网络---->网络理论
网络理论 网络协议分层模型网络数据的封装于分用地址管理 网络协议分层模型 OSI五层模型:应用层,传输层,网络层,数据链路层,物理层 应用层:主要负责应用程序间的沟通,代表协议有HTML协议&#x…...
Android学习之路(4) UI控件之输入框
本节引言: 在本节中,我们来学习第二个很常用的控件EditText(输入框); 和TextView非常类似,最大的区别是:EditText可以接受用户输入! 1.设置默认提示文本 如下图,相信你对于这种用户登录的界面并…...

1.初识Web
文章目录 1. 什么是Web?2.初始Web前端2.1.Web标准 1. 什么是Web? web:全球广域网,也称万维网(www World Wide Web),能够通过浏览器访问的网站。 2.初始Web前端 网页有哪些部分组成? 文字、图片、音频、视频、超链接… 我们看到的网页&am…...
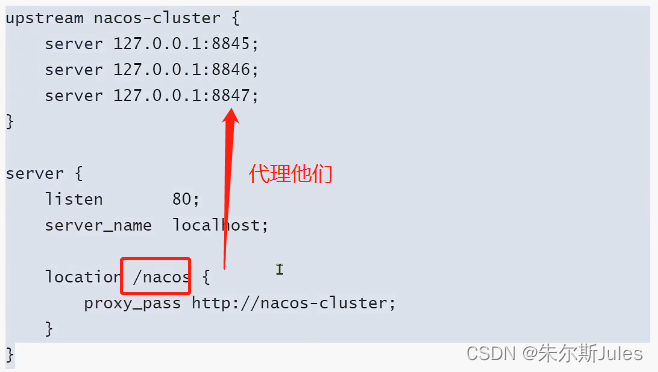
【微服务技术一】Eureka、Nacos、Ribbon(配置管理、注册中心、负载均衡)
微服务技术一 技术栈图一、注册中心Eureka概念:搭建EurekaServer服务注册服务发现(消费者对提供者的远程调用) 二、Ribbon负载均衡负载均衡的原理:LoadBalanced负载均衡的策略:IRule懒加载 三、Nacos注册中心Nacos的安…...
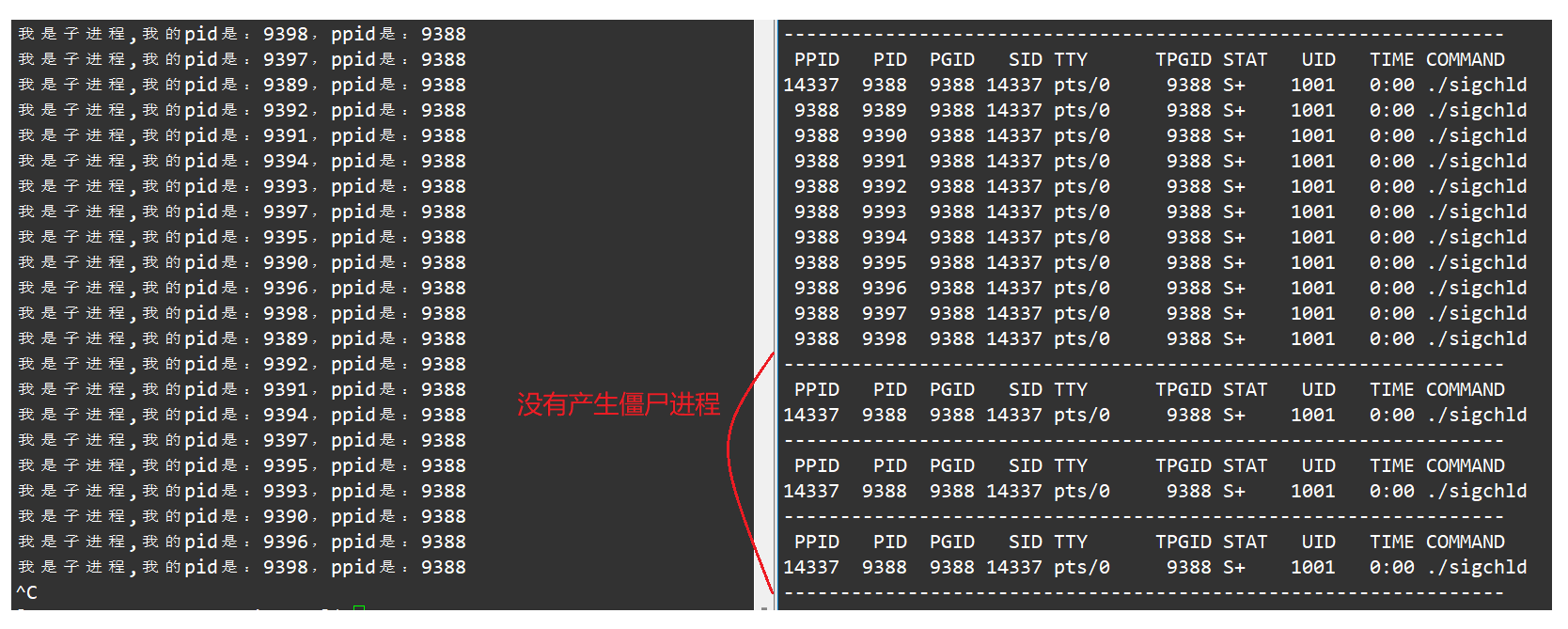
【Linux】可重入函数 volatile关键字 以及SIGCHLD信号
可重入函数 volatile关键字 以及SIGCHLD信号 一、可重入函数1、引入2、可重入函数的判断 二、volatile关键字1、引入2、关于编译器的优化的简单讨论 三、SIGCHLD信号 一、可重入函数 1、引入 我们来先看一个例子来帮助我们理解什么是可重入函数: 假设我们现在要对…...
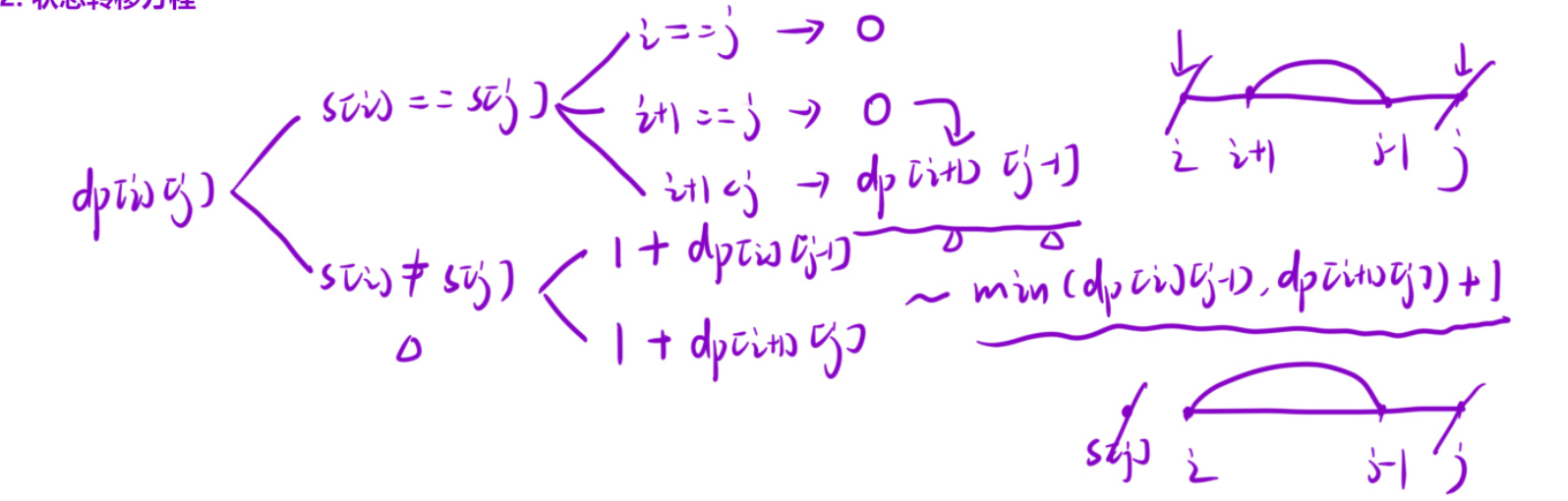
【动态规划】回文串问题
文章目录 动态规划(回文串问题)1. 回文子串2. 最长回文子串3. 回文串分割 IV4. 分割回文串 ||5. 最长回文子序列6. 让字符串成为回文串的最小插入次数 动态规划(回文串问题) 1. 回文子串 题目链接 状态表示 f[i][j]表示 i 到 j …...

Laravel Swift Mail发送带附件的邮件报错 “Swift_IoException The path cannot be empty“处理
先说下情况,就是我要做一个发送附件的邮件发送功能,结果,报错:The path cannot be empty。给我整的有点迷糊,网上也没有类似的问题。后来,我检查了一下代码,发现有个地方,是需要给附…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...
